5.6二元一次方程与一次函数同步练习题 2021-2022学年北师大版八年级数学上册(Word版 含答案)
文档属性
| 名称 | 5.6二元一次方程与一次函数同步练习题 2021-2022学年北师大版八年级数学上册(Word版 含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 163.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-17 23:41:37 | ||
图片预览




文档简介
5.6二元一次方程与一次函数同步练习题 2021-2022学年北师大版八年级数学上册
A组(基础题)
一、填空题
1.二元一次方程2x+y=4有无数个解,以它的每一个解为坐标的点都在一次函数___________的图象上,反过来,一次函数_______________的图象上的每一个点的坐标均适合二元一次方程2x+y=4.
2.关于x,y的二元一次方程组的解是如图,在平面直角坐标系xOy中,直线l1:y=mx-5与直线l2:y=nx-b相交于点P,则点P的坐标为___________.
3.如图,已知函数y=x+1和y=ax+3图象交于点P,点P的横坐标为1,则关于x,y的方程组的解是___________
4.直线y=ax+b和直线y=bx+3a的交点坐标是(2,-1),则a=___________,b=___________
二、选择题
5.下面四条直线,其中直线上的每一个点的坐标都是二元一次方程2x-3y=6的解的是( )
6.如图,函数y=ax+b和y=kx的图象交于点P,则关于x,y的方程组的解是( )
A. B. C. D.
7.已知一次函数y1=2x+m与y2=2x+n(m≠n)的图象如图所示,则关于x与y的二元一次方程组的解有( )
A.0个 B.1个 C.2个 D.无数个
8.若方程组无解,则一次函数y=2-x与y=-x的图象必定( )
A.重合 B.平行 C.相交 D.无法判断
9.如果关于x,y的方程组无解,那么直线y=-(k+3)x-k不经过的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
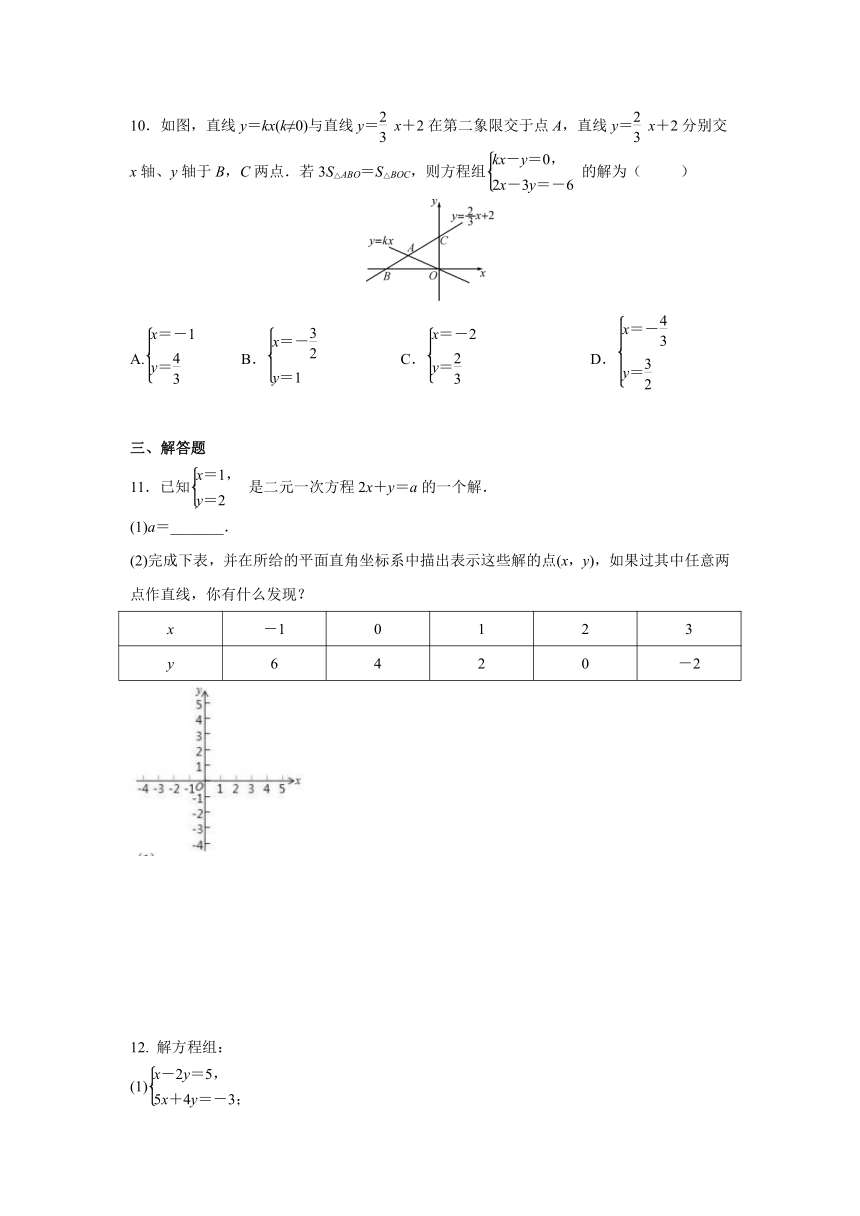
10.如图,直线y=kx(k≠0)与直线y=x+2在第二象限交于点A,直线y=x+2分别交x轴、y轴于B,C两点.若3S△ABO=S△BOC,则方程组的解为( )
A. B. C. D.
三、解答题
11.已知是二元一次方程2x+y=a的一个解.
(1)a=_______.
(2)完成下表,并在所给的平面直角坐标系中描出表示这些解的点(x,y),如果过其中任意两点作直线,你有什么发现?
x
-1
0
1
2
3
y
6
4
2
0
-2
12. 解方程组:
(1)
(2)(用作图法求解)
B组(中档题)
四、填空题
13.若方程组有无数解,则k-m的值是__________.
14.元朝朱世杰的《算学启蒙》一书记载了这样一道数学题:“今有良马日行二百四十里,驽马日行一百五十里.驽马先行一十二日,问良马几何日追及之.”如图是两匹马行走路程s(里)关于行走时间t(日)的函数图象,则两图象交点P的坐标是___________.
五、解答题
15.某游泳馆普通票价为30元/张,暑假为了促销,新推出一种优惠卡,其售价为300元/张,每次凭卡另收15元.暑假普通票正常出售,优惠卡仅限暑假使用,不限次数.设游泳x次时,所需总费用为y元.
(1)分别写出选择优惠卡、普通票消费时,y与x之间的函数关系式.
(2)在同一平面直角坐标系中若两种消费方式对应的函数图象如图所示,请求出点A,B的坐标.
C组(综合题)
16.正方形OABC的边长为2,其中OA,OC分别在x轴和y轴上,如图1所示,直线l经过A,C两点.
(1)若点P是直线l上的一点,当△OPA的面积是3时,请求出点P的坐标.
(2)如图2,坐标系xOy内有一点D(-1,2),点E是直线l上的一个动点,请求出|BE+DE|的最小值和此时点E的坐标.
参考答案
5.6二元一次方程与一次函数同步练习题 2021-2022学年北师大版八年级数学上册
A组(基础题)
一、填空题
1.二元一次方程2x+y=4有无数个解,以它的每一个解为坐标的点都在一次函数y=-2x+4的图象上,反过来,一次函数y=-2x+4的图象上的每一个点的坐标均适合二元一次方程2x+y=4.
2.关于x,y的二元一次方程组的解是如图,在平面直角坐标系xOy中,直线l1:y=mx-5与直线l2:y=nx-b相交于点P,则点P的坐标为(1,2).
3.如图,已知函数y=x+1和y=ax+3图象交于点P,点P的横坐标为1,则关于x,y的方程组的解是.
4.直线y=ax+b和直线y=bx+3a的交点坐标是(2,-1),则a=-1,b=1.
二、选择题
5.下面四条直线,其中直线上的每一个点的坐标都是二元一次方程2x-3y=6的解的是( D )
6.如图,函数y=ax+b和y=kx的图象交于点P,则关于x,y的方程组的解是( D )
A. B. C. D.
7.已知一次函数y1=2x+m与y2=2x+n(m≠n)的图象如图所示,则关于x与y的二元一次方程组的解有( A )
A.0个 B.1个 C.2个 D.无数个
8.若方程组无解,则一次函数y=2-x与y=-x的图象必定( B )
A.重合 B.平行 C.相交 D.无法判断
9.如果关于x,y的方程组无解,那么直线y=-(k+3)x-k不经过的象限是( C )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
10.如图,直线y=kx(k≠0)与直线y=x+2在第二象限交于点A,直线y=x+2分别交x轴、y轴于B,C两点.若3S△ABO=S△BOC,则方程组的解为( C )
A. B. C. D.
三、解答题
11.已知是二元一次方程2x+y=a的一个解.
(1)a=4.
(2)完成下表,并在所给的平面直角坐标系中描出表示这些解的点(x,y),如果过其中任意两点作直线,你有什么发现?
x
-1
0
1
2
3
y
6
4
2
0
-2
解:填表如上,描点、连线如图.
由图可知,如果过其中任意两点作直线,其他点也在这条直线上.
12 解方程组:
(1)
解:
(2)(用作图法求解)
解:原方程组变形为
作图如图.
∴的解为
B组(中档题)
四、填空题
13.若方程组有无数解,则k-m的值是4.
14.元朝朱世杰的《算学启蒙》一书记载了这样一道数学题:“今有良马日行二百四十里,驽马日行一百五十里.驽马先行一十二日,问良马几何日追及之.”如图是两匹马行走路程s(里)关于行走时间t(日)的函数图象,则两图象交点P的坐标是(32,4800).
五、解答题
15.某游泳馆普通票价为30元/张,暑假为了促销,新推出一种优惠卡,其售价为300元/张,每次凭卡另收15元.暑假普通票正常出售,优惠卡仅限暑假使用,不限次数.设游泳x次时,所需总费用为y元.
(1)分别写出选择优惠卡、普通票消费时,y与x之间的函数关系式.
(2)在同一平面直角坐标系中若两种消费方式对应的函数图象如图所示,请求出点A,B的坐标.
解:①由题意知,
当选择优惠卡时,y与x的函数关系式为y=300+15x;
当选择普通卡时,y与x的函数关系式为y=30x.
②将x=0代入y=300+15x,得y=300,即点A的坐标为(0,300).
令300+15x=30x,得x=20,则30x=600,即点B的坐标为(20,600).
C组(综合题)
16.正方形OABC的边长为2,其中OA,OC分别在x轴和y轴上,如图1所示,直线l经过A,C两点.
(1)若点P是直线l上的一点,当△OPA的面积是3时,请求出点P的坐标.
(2)如图2,坐标系xOy内有一点D(-1,2),点E是直线l上的一个动点,请求出|BE+DE|的最小值和此时点E的坐标.
图1 图2
解:(1)由题意可知,点A、点C的坐标分别为(-2,0)和(0,2).
设直线l的表达式为y=kx+b(k≠0),由直线l经过点A(-2,0)和点C(0,2),得
解得
∴直线l的表达式为y=x+2.
∵点P是直线l上的点,所以设点P的坐标为(m,m+2).
由题意,得×2×|m+2|=3,解得m=1或m=-5.
∴P的坐标为(1,3)或(-5,-3).
(2)连接OD交直线l于点E,则点E为所求,此时|BE+DE|=|OE+DE|=OD,OD即为最小值.
设直线OD的表达式为y=k1x(k1≠0),
∵直线经过点D(-1,2),∴2=-k1,即k1=-2.
∴直线OD的表达式为y=-2x.
由解得
∴点E的坐标为(-,).
∵点D的坐标为(-1,2),∴OC=2,DC=1.
∴由勾股定理可得,OD=,即|BE+DE|的最小值为.
A组(基础题)
一、填空题
1.二元一次方程2x+y=4有无数个解,以它的每一个解为坐标的点都在一次函数___________的图象上,反过来,一次函数_______________的图象上的每一个点的坐标均适合二元一次方程2x+y=4.
2.关于x,y的二元一次方程组的解是如图,在平面直角坐标系xOy中,直线l1:y=mx-5与直线l2:y=nx-b相交于点P,则点P的坐标为___________.
3.如图,已知函数y=x+1和y=ax+3图象交于点P,点P的横坐标为1,则关于x,y的方程组的解是___________
4.直线y=ax+b和直线y=bx+3a的交点坐标是(2,-1),则a=___________,b=___________
二、选择题
5.下面四条直线,其中直线上的每一个点的坐标都是二元一次方程2x-3y=6的解的是( )
6.如图,函数y=ax+b和y=kx的图象交于点P,则关于x,y的方程组的解是( )
A. B. C. D.
7.已知一次函数y1=2x+m与y2=2x+n(m≠n)的图象如图所示,则关于x与y的二元一次方程组的解有( )
A.0个 B.1个 C.2个 D.无数个
8.若方程组无解,则一次函数y=2-x与y=-x的图象必定( )
A.重合 B.平行 C.相交 D.无法判断
9.如果关于x,y的方程组无解,那么直线y=-(k+3)x-k不经过的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
10.如图,直线y=kx(k≠0)与直线y=x+2在第二象限交于点A,直线y=x+2分别交x轴、y轴于B,C两点.若3S△ABO=S△BOC,则方程组的解为( )
A. B. C. D.
三、解答题
11.已知是二元一次方程2x+y=a的一个解.
(1)a=_______.
(2)完成下表,并在所给的平面直角坐标系中描出表示这些解的点(x,y),如果过其中任意两点作直线,你有什么发现?
x
-1
0
1
2
3
y
6
4
2
0
-2
12. 解方程组:
(1)
(2)(用作图法求解)
B组(中档题)
四、填空题
13.若方程组有无数解,则k-m的值是__________.
14.元朝朱世杰的《算学启蒙》一书记载了这样一道数学题:“今有良马日行二百四十里,驽马日行一百五十里.驽马先行一十二日,问良马几何日追及之.”如图是两匹马行走路程s(里)关于行走时间t(日)的函数图象,则两图象交点P的坐标是___________.
五、解答题
15.某游泳馆普通票价为30元/张,暑假为了促销,新推出一种优惠卡,其售价为300元/张,每次凭卡另收15元.暑假普通票正常出售,优惠卡仅限暑假使用,不限次数.设游泳x次时,所需总费用为y元.
(1)分别写出选择优惠卡、普通票消费时,y与x之间的函数关系式.
(2)在同一平面直角坐标系中若两种消费方式对应的函数图象如图所示,请求出点A,B的坐标.
C组(综合题)
16.正方形OABC的边长为2,其中OA,OC分别在x轴和y轴上,如图1所示,直线l经过A,C两点.
(1)若点P是直线l上的一点,当△OPA的面积是3时,请求出点P的坐标.
(2)如图2,坐标系xOy内有一点D(-1,2),点E是直线l上的一个动点,请求出|BE+DE|的最小值和此时点E的坐标.
参考答案
5.6二元一次方程与一次函数同步练习题 2021-2022学年北师大版八年级数学上册
A组(基础题)
一、填空题
1.二元一次方程2x+y=4有无数个解,以它的每一个解为坐标的点都在一次函数y=-2x+4的图象上,反过来,一次函数y=-2x+4的图象上的每一个点的坐标均适合二元一次方程2x+y=4.
2.关于x,y的二元一次方程组的解是如图,在平面直角坐标系xOy中,直线l1:y=mx-5与直线l2:y=nx-b相交于点P,则点P的坐标为(1,2).
3.如图,已知函数y=x+1和y=ax+3图象交于点P,点P的横坐标为1,则关于x,y的方程组的解是.
4.直线y=ax+b和直线y=bx+3a的交点坐标是(2,-1),则a=-1,b=1.
二、选择题
5.下面四条直线,其中直线上的每一个点的坐标都是二元一次方程2x-3y=6的解的是( D )
6.如图,函数y=ax+b和y=kx的图象交于点P,则关于x,y的方程组的解是( D )
A. B. C. D.
7.已知一次函数y1=2x+m与y2=2x+n(m≠n)的图象如图所示,则关于x与y的二元一次方程组的解有( A )
A.0个 B.1个 C.2个 D.无数个
8.若方程组无解,则一次函数y=2-x与y=-x的图象必定( B )
A.重合 B.平行 C.相交 D.无法判断
9.如果关于x,y的方程组无解,那么直线y=-(k+3)x-k不经过的象限是( C )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
10.如图,直线y=kx(k≠0)与直线y=x+2在第二象限交于点A,直线y=x+2分别交x轴、y轴于B,C两点.若3S△ABO=S△BOC,则方程组的解为( C )
A. B. C. D.
三、解答题
11.已知是二元一次方程2x+y=a的一个解.
(1)a=4.
(2)完成下表,并在所给的平面直角坐标系中描出表示这些解的点(x,y),如果过其中任意两点作直线,你有什么发现?
x
-1
0
1
2
3
y
6
4
2
0
-2
解:填表如上,描点、连线如图.
由图可知,如果过其中任意两点作直线,其他点也在这条直线上.
12 解方程组:
(1)
解:
(2)(用作图法求解)
解:原方程组变形为
作图如图.
∴的解为
B组(中档题)
四、填空题
13.若方程组有无数解,则k-m的值是4.
14.元朝朱世杰的《算学启蒙》一书记载了这样一道数学题:“今有良马日行二百四十里,驽马日行一百五十里.驽马先行一十二日,问良马几何日追及之.”如图是两匹马行走路程s(里)关于行走时间t(日)的函数图象,则两图象交点P的坐标是(32,4800).
五、解答题
15.某游泳馆普通票价为30元/张,暑假为了促销,新推出一种优惠卡,其售价为300元/张,每次凭卡另收15元.暑假普通票正常出售,优惠卡仅限暑假使用,不限次数.设游泳x次时,所需总费用为y元.
(1)分别写出选择优惠卡、普通票消费时,y与x之间的函数关系式.
(2)在同一平面直角坐标系中若两种消费方式对应的函数图象如图所示,请求出点A,B的坐标.
解:①由题意知,
当选择优惠卡时,y与x的函数关系式为y=300+15x;
当选择普通卡时,y与x的函数关系式为y=30x.
②将x=0代入y=300+15x,得y=300,即点A的坐标为(0,300).
令300+15x=30x,得x=20,则30x=600,即点B的坐标为(20,600).
C组(综合题)
16.正方形OABC的边长为2,其中OA,OC分别在x轴和y轴上,如图1所示,直线l经过A,C两点.
(1)若点P是直线l上的一点,当△OPA的面积是3时,请求出点P的坐标.
(2)如图2,坐标系xOy内有一点D(-1,2),点E是直线l上的一个动点,请求出|BE+DE|的最小值和此时点E的坐标.
图1 图2
解:(1)由题意可知,点A、点C的坐标分别为(-2,0)和(0,2).
设直线l的表达式为y=kx+b(k≠0),由直线l经过点A(-2,0)和点C(0,2),得
解得
∴直线l的表达式为y=x+2.
∵点P是直线l上的点,所以设点P的坐标为(m,m+2).
由题意,得×2×|m+2|=3,解得m=1或m=-5.
∴P的坐标为(1,3)或(-5,-3).
(2)连接OD交直线l于点E,则点E为所求,此时|BE+DE|=|OE+DE|=OD,OD即为最小值.
设直线OD的表达式为y=k1x(k1≠0),
∵直线经过点D(-1,2),∴2=-k1,即k1=-2.
∴直线OD的表达式为y=-2x.
由解得
∴点E的坐标为(-,).
∵点D的坐标为(-1,2),∴OC=2,DC=1.
∴由勾股定理可得,OD=,即|BE+DE|的最小值为.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
