7.4 平行线的性质 同步练习题 2021-2022学年北师大版数学八年级上册(Word版 含答案)
文档属性
| 名称 | 7.4 平行线的性质 同步练习题 2021-2022学年北师大版数学八年级上册(Word版 含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 119.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-18 09:55:20 | ||
图片预览



文档简介
7.4 平行线的性质 同步练习题(含答案)2021-2022学年北师大版八年级数学上册
A组(基础题)
一、填空题
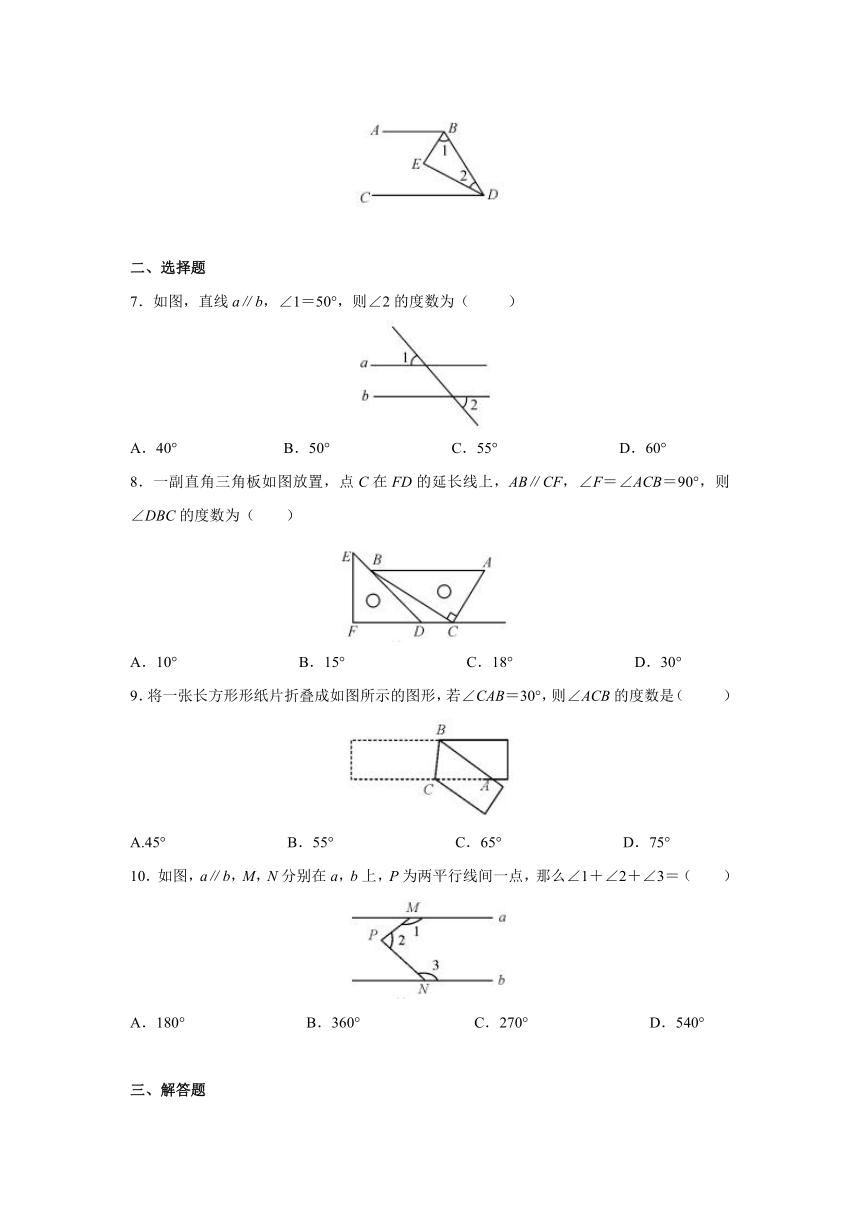
1.如图,直线l1,l2被直线l3所截,已知l1∥l2,∠1=80°,则∠2=_____.
2.如图,a∥b,若∠1=50°,则∠2=_____.
3.如图,AB∥CD,AB⊥AE,∠CAE=42°,则∠ACD的度数为_____.
4.如图,直线a∥b,∠BAC的顶点A在直线a上,且∠BAC=98°,若∠1=35°,则∠2=_____.
5.如图,AB∥CD,DE∥CB,∠B=35°,则∠D=_____.
6.如图,AB∥CD,∠ABD的平分线与∠BDC的平分线交于点E,则∠1+∠2=_____.
二、选择题
7.如图,直线a∥b,∠1=50°,则∠2的度数为( )
A.40° B.50° C.55° D.60°
8.一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,则∠DBC的度数为( )
A.10° B.15° C.18° D.30°
9.将一张长方形形纸片折叠成如图所示的图形,若∠CAB=30°,则∠ACB的度数是( )
A.45° B.55° C.65° D.75°
10.如图,a∥b,M,N分别在a,b上,P为两平行线间一点,那么∠1+∠2+∠3=( )
A.180° B.360° C.270° D.540°
三、解答题
11.光线在不同介质中的传播速度不同,从一种介质射向另一种介质时会发生折射.如图,水面AB与水杯下沿CD平行,光线EF从水中射向空气时发生折射,沿FH传播,点G在射线EF上,已知∠HFB=20°,∠FED=45°,求∠GFH的度数.
12.如图,AB∥CD,∠B=72°,EF平分∠BEC,EG⊥EF,求∠DEG的度数.
13.如图,已知AB∥DE∥CF,若∠ABC=70°,∠CDE=130°,求∠BCD的度数.
14.如图,已知AD⊥BC于点D,EG⊥BC于点G,∠E=∠1.求证:AD平分∠BAC.
B组(中档题)
四、填空题
15.如图,直线l1∥l2,∠1=30°,则∠2+∠3=_____.
16.如图,CD平分∠ACB,∠1+∠2=180°,∠3=∠A,∠4=35°,则∠CED=_____.
17.如图,AB∥CD,EG,EM,FM分别平分∠AEF,∠BEF,∠EFD,则图中与∠DFM相等的角(不含它本身)有_____个.
五、解答题
18.如图,直线AB∥CD,直线EF⊥AB,点M在CD上,MP平分∠GMC,PN平分∠EGM,且∠CMG+∠MGF=90°.
(1)若∠MGN=75°,∠CMG=60°,求∠MPN的度数.
(2)若∠MGF=40°,∠CMG=50°,求∠MPN的度数.
(3)若点M在直线CD上移动,∠MPN的大小是否发生变化?如果保持不变,请直接写出∠MPN的值;如果发生变化,请直接写出∠MPN的变化范围.
C组(综合题)
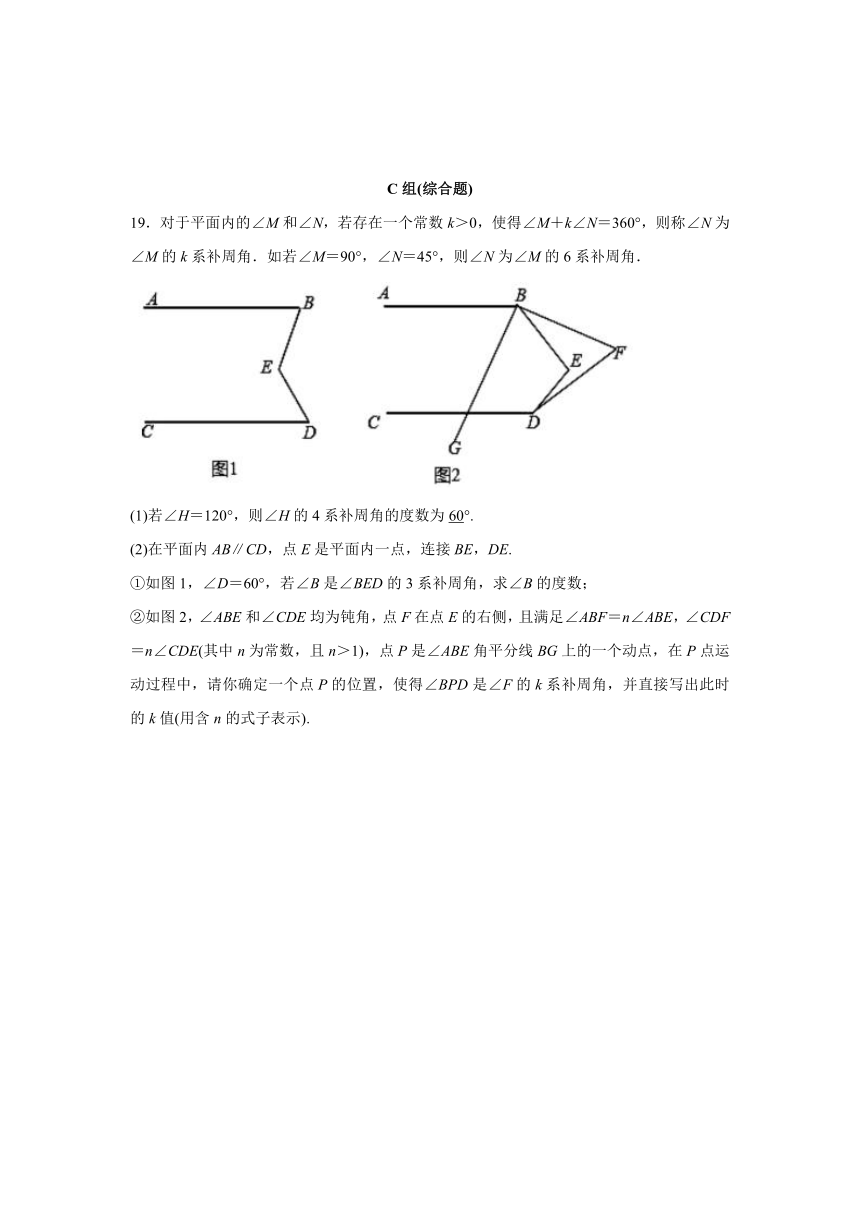
19.对于平面内的∠M和∠N,若存在一个常数k>0,使得∠M+k∠N=360°,则称∠N为∠M的k系补周角.如若∠M=90°,∠N=45°,则∠N为∠M的6系补周角.
(1)若∠H=120°,则∠H的4系补周角的度数为60°.
(2)在平面内AB∥CD,点E是平面内一点,连接BE,DE.
①如图1,∠D=60°,若∠B是∠BED的3系补周角,求∠B的度数;
②如图2,∠ABE和∠CDE均为钝角,点F在点E的右侧,且满足∠ABF=n∠ABE,∠CDF=n∠CDE(其中n为常数,且n>1),点P是∠ABE角平分线BG上的一个动点,在P点运动过程中,请你确定一个点P的位置,使得∠BPD是∠F的k系补周角,并直接写出此时的k值(用含n的式子表示).
参考答案
7.4 平行线的性质 同步练习题 2021-2022学年北师大版八年级数学上册
A组(基础题)
一、填空题
1.如图,直线l1,l2被直线l3所截,已知l1∥l2,∠1=80°,则∠2=80°.
2.如图,a∥b,若∠1=50°,则∠2=130°.
3.如图,AB∥CD,AB⊥AE,∠CAE=42°,则∠ACD的度数为132°.
4.如图,直线a∥b,∠BAC的顶点A在直线a上,且∠BAC=98°,若∠1=35°,则∠2=47°.
5.如图,AB∥CD,DE∥CB,∠B=35°,则∠D=145°.
6.如图,AB∥CD,∠ABD的平分线与∠BDC的平分线交于点E,则∠1+∠2=90°.
二、选择题
7.如图,直线a∥b,∠1=50°,则∠2的度数为( B )
A.40° B.50° C.55° D.60°
8.一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,则∠DBC的度数为( B )
A.10° B.15° C.18° D.30°
9.将一张长方形形纸片折叠成如图所示的图形,若∠CAB=30°,则∠ACB的度数是( D )
A.45° B.55° C.65° D.75°
10.如图,a∥b,M,N分别在a,b上,P为两平行线间一点,那么∠1+∠2+∠3=( B )
A.180° B.360° C.270° D.540°
三、解答题
11.光线在不同介质中的传播速度不同,从一种介质射向另一种介质时会发生折射.如图,水面AB与水杯下沿CD平行,光线EF从水中射向空气时发生折射,沿FH传播,点G在射线EF上,已知∠HFB=20°,∠FED=45°,求∠GFH的度数.
解:∵AB∥CD,
∴∠GFB=∠FED=45°.
∵∠HFB=20°,
∴∠GFH=∠GFB-∠HFB=45°-20°=25°.
12.如图,AB∥CD,∠B=72°,EF平分∠BEC,EG⊥EF,求∠DEG的度数.
解:∵AB∥CD,
∴∠B=∠DEB=72°.
∵EF平分∠BEC,
∴∠BEF=∠CEF.
∵EF⊥EG,
∴∠FEG=90°.
∴∠DEG+∠CEF=90°,∠BEG+∠BEF=90°.
∴∠DEG=∠BEG=∠DEB=36°.
13.如图,已知AB∥DE∥CF,若∠ABC=70°,∠CDE=130°,求∠BCD的度数.
解:∵AB∥CF,∠ABC=70°,
∴∠BCF=∠ABC=70°.
又∵DE∥CF,∠CDE=130°,
∴∠DCF=180°-∠CDE=50°.
∴∠BCD=∠BCF-∠DCF=70°-50°=20°.
14.如图,已知AD⊥BC于点D,EG⊥BC于点G,∠E=∠1.求证:AD平分∠BAC.
证明:∵AD⊥BC于点D,EG⊥BC于点G,
∴∠ADC=∠EGC=90°.
∴AD∥EG.
∴∠1=∠2,∠E=∠3.
又∵∠E=∠1,
∴∠2=∠3.
∴AD平分∠BAC.
B组(中档题)
四、填空题
15.如图,直线l1∥l2,∠1=30°,则∠2+∠3=210°.
16.如图,CD平分∠ACB,∠1+∠2=180°,∠3=∠A,∠4=35°,则∠CED=110°.
17.如图,AB∥CD,EG,EM,FM分别平分∠AEF,∠BEF,∠EFD,则图中与∠DFM相等的角(不含它本身)有7个.
五、解答题
18.如图,直线AB∥CD,直线EF⊥AB,点M在CD上,MP平分∠GMC,PN平分∠EGM,且∠CMG+∠MGF=90°.
(1)若∠MGN=75°,∠CMG=60°,求∠MPN的度数.
(2)若∠MGF=40°,∠CMG=50°,求∠MPN的度数.
(3)若点M在直线CD上移动,∠MPN的大小是否发生变化?如果保持不变,请直接写出∠MPN的值;如果发生变化,请直接写出∠MPN的变化范围.
解:(1)∵∠CMG=60°,MP平分∠GMC,
∴∠PMG=60°÷2=30°.
∵∠MGN=75°,∠MGN=∠MPN+∠PMG,
∴∠MPN=70°-30°=45°.
(2)∵∠MGF=30°,
∴∠EGM=180°-40°=140°.
∵PN平分∠EGM,
∴∠MGN=140°÷2=70°.
∵∠CMG=50°,MP平分∠GMC,
∴∠PMG=50°÷2=25°.
∵∠MGN=70°,∠MGN=∠MPN+∠PMG,
∴∠MPN=70°-25°=45°.
(3)当点M在直线CD上移动时,∠MPN的大小不变,都是45°.
C组(综合题)
19.对于平面内的∠M和∠N,若存在一个常数k>0,使得∠M+k∠N=360°,则称∠N为∠M的k系补周角.如若∠M=90°,∠N=45°,则∠N为∠M的6系补周角.
(1)若∠H=120°,则∠H的4系补周角的度数为60°.
(2)在平面内AB∥CD,点E是平面内一点,连接BE,DE.
①如图1,∠D=60°,若∠B是∠BED的3系补周角,求∠B的度数;
②如图2,∠ABE和∠CDE均为钝角,点F在点E的右侧,且满足∠ABF=n∠ABE,∠CDF=n∠CDE(其中n为常数,且n>1),点P是∠ABE角平分线BG上的一个动点,在P点运动过程中,请你确定一个点P的位置,使得∠BPD是∠F的k系补周角,并直接写出此时的k值(用含n的式子表示).
解:(2)①过E作EF∥AB,
∴∠B=∠BEF.
∵AB∥CD,
∴EF∥CD.
∴∠D=∠DEF=60°.
∵∠B+60°=∠BEF+∠DEF,
∴∠B+60°=∠BED.
∵∠B是∠BED的3系补周角,
∴∠BED=360°-3∠B.
∴∠B+60°=360°-3∠B.
∴∠B=75°.
②当BG上的动点P为∠CDE的角平分线与BG的交点时,满足∠BPD是∠F的k系补周角,此时k=2n.
A组(基础题)
一、填空题
1.如图,直线l1,l2被直线l3所截,已知l1∥l2,∠1=80°,则∠2=_____.
2.如图,a∥b,若∠1=50°,则∠2=_____.
3.如图,AB∥CD,AB⊥AE,∠CAE=42°,则∠ACD的度数为_____.
4.如图,直线a∥b,∠BAC的顶点A在直线a上,且∠BAC=98°,若∠1=35°,则∠2=_____.
5.如图,AB∥CD,DE∥CB,∠B=35°,则∠D=_____.
6.如图,AB∥CD,∠ABD的平分线与∠BDC的平分线交于点E,则∠1+∠2=_____.
二、选择题
7.如图,直线a∥b,∠1=50°,则∠2的度数为( )
A.40° B.50° C.55° D.60°
8.一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,则∠DBC的度数为( )
A.10° B.15° C.18° D.30°
9.将一张长方形形纸片折叠成如图所示的图形,若∠CAB=30°,则∠ACB的度数是( )
A.45° B.55° C.65° D.75°
10.如图,a∥b,M,N分别在a,b上,P为两平行线间一点,那么∠1+∠2+∠3=( )
A.180° B.360° C.270° D.540°
三、解答题
11.光线在不同介质中的传播速度不同,从一种介质射向另一种介质时会发生折射.如图,水面AB与水杯下沿CD平行,光线EF从水中射向空气时发生折射,沿FH传播,点G在射线EF上,已知∠HFB=20°,∠FED=45°,求∠GFH的度数.
12.如图,AB∥CD,∠B=72°,EF平分∠BEC,EG⊥EF,求∠DEG的度数.
13.如图,已知AB∥DE∥CF,若∠ABC=70°,∠CDE=130°,求∠BCD的度数.
14.如图,已知AD⊥BC于点D,EG⊥BC于点G,∠E=∠1.求证:AD平分∠BAC.
B组(中档题)
四、填空题
15.如图,直线l1∥l2,∠1=30°,则∠2+∠3=_____.
16.如图,CD平分∠ACB,∠1+∠2=180°,∠3=∠A,∠4=35°,则∠CED=_____.
17.如图,AB∥CD,EG,EM,FM分别平分∠AEF,∠BEF,∠EFD,则图中与∠DFM相等的角(不含它本身)有_____个.
五、解答题
18.如图,直线AB∥CD,直线EF⊥AB,点M在CD上,MP平分∠GMC,PN平分∠EGM,且∠CMG+∠MGF=90°.
(1)若∠MGN=75°,∠CMG=60°,求∠MPN的度数.
(2)若∠MGF=40°,∠CMG=50°,求∠MPN的度数.
(3)若点M在直线CD上移动,∠MPN的大小是否发生变化?如果保持不变,请直接写出∠MPN的值;如果发生变化,请直接写出∠MPN的变化范围.
C组(综合题)
19.对于平面内的∠M和∠N,若存在一个常数k>0,使得∠M+k∠N=360°,则称∠N为∠M的k系补周角.如若∠M=90°,∠N=45°,则∠N为∠M的6系补周角.
(1)若∠H=120°,则∠H的4系补周角的度数为60°.
(2)在平面内AB∥CD,点E是平面内一点,连接BE,DE.
①如图1,∠D=60°,若∠B是∠BED的3系补周角,求∠B的度数;
②如图2,∠ABE和∠CDE均为钝角,点F在点E的右侧,且满足∠ABF=n∠ABE,∠CDF=n∠CDE(其中n为常数,且n>1),点P是∠ABE角平分线BG上的一个动点,在P点运动过程中,请你确定一个点P的位置,使得∠BPD是∠F的k系补周角,并直接写出此时的k值(用含n的式子表示).
参考答案
7.4 平行线的性质 同步练习题 2021-2022学年北师大版八年级数学上册
A组(基础题)
一、填空题
1.如图,直线l1,l2被直线l3所截,已知l1∥l2,∠1=80°,则∠2=80°.
2.如图,a∥b,若∠1=50°,则∠2=130°.
3.如图,AB∥CD,AB⊥AE,∠CAE=42°,则∠ACD的度数为132°.
4.如图,直线a∥b,∠BAC的顶点A在直线a上,且∠BAC=98°,若∠1=35°,则∠2=47°.
5.如图,AB∥CD,DE∥CB,∠B=35°,则∠D=145°.
6.如图,AB∥CD,∠ABD的平分线与∠BDC的平分线交于点E,则∠1+∠2=90°.
二、选择题
7.如图,直线a∥b,∠1=50°,则∠2的度数为( B )
A.40° B.50° C.55° D.60°
8.一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,则∠DBC的度数为( B )
A.10° B.15° C.18° D.30°
9.将一张长方形形纸片折叠成如图所示的图形,若∠CAB=30°,则∠ACB的度数是( D )
A.45° B.55° C.65° D.75°
10.如图,a∥b,M,N分别在a,b上,P为两平行线间一点,那么∠1+∠2+∠3=( B )
A.180° B.360° C.270° D.540°
三、解答题
11.光线在不同介质中的传播速度不同,从一种介质射向另一种介质时会发生折射.如图,水面AB与水杯下沿CD平行,光线EF从水中射向空气时发生折射,沿FH传播,点G在射线EF上,已知∠HFB=20°,∠FED=45°,求∠GFH的度数.
解:∵AB∥CD,
∴∠GFB=∠FED=45°.
∵∠HFB=20°,
∴∠GFH=∠GFB-∠HFB=45°-20°=25°.
12.如图,AB∥CD,∠B=72°,EF平分∠BEC,EG⊥EF,求∠DEG的度数.
解:∵AB∥CD,
∴∠B=∠DEB=72°.
∵EF平分∠BEC,
∴∠BEF=∠CEF.
∵EF⊥EG,
∴∠FEG=90°.
∴∠DEG+∠CEF=90°,∠BEG+∠BEF=90°.
∴∠DEG=∠BEG=∠DEB=36°.
13.如图,已知AB∥DE∥CF,若∠ABC=70°,∠CDE=130°,求∠BCD的度数.
解:∵AB∥CF,∠ABC=70°,
∴∠BCF=∠ABC=70°.
又∵DE∥CF,∠CDE=130°,
∴∠DCF=180°-∠CDE=50°.
∴∠BCD=∠BCF-∠DCF=70°-50°=20°.
14.如图,已知AD⊥BC于点D,EG⊥BC于点G,∠E=∠1.求证:AD平分∠BAC.
证明:∵AD⊥BC于点D,EG⊥BC于点G,
∴∠ADC=∠EGC=90°.
∴AD∥EG.
∴∠1=∠2,∠E=∠3.
又∵∠E=∠1,
∴∠2=∠3.
∴AD平分∠BAC.
B组(中档题)
四、填空题
15.如图,直线l1∥l2,∠1=30°,则∠2+∠3=210°.
16.如图,CD平分∠ACB,∠1+∠2=180°,∠3=∠A,∠4=35°,则∠CED=110°.
17.如图,AB∥CD,EG,EM,FM分别平分∠AEF,∠BEF,∠EFD,则图中与∠DFM相等的角(不含它本身)有7个.
五、解答题
18.如图,直线AB∥CD,直线EF⊥AB,点M在CD上,MP平分∠GMC,PN平分∠EGM,且∠CMG+∠MGF=90°.
(1)若∠MGN=75°,∠CMG=60°,求∠MPN的度数.
(2)若∠MGF=40°,∠CMG=50°,求∠MPN的度数.
(3)若点M在直线CD上移动,∠MPN的大小是否发生变化?如果保持不变,请直接写出∠MPN的值;如果发生变化,请直接写出∠MPN的变化范围.
解:(1)∵∠CMG=60°,MP平分∠GMC,
∴∠PMG=60°÷2=30°.
∵∠MGN=75°,∠MGN=∠MPN+∠PMG,
∴∠MPN=70°-30°=45°.
(2)∵∠MGF=30°,
∴∠EGM=180°-40°=140°.
∵PN平分∠EGM,
∴∠MGN=140°÷2=70°.
∵∠CMG=50°,MP平分∠GMC,
∴∠PMG=50°÷2=25°.
∵∠MGN=70°,∠MGN=∠MPN+∠PMG,
∴∠MPN=70°-25°=45°.
(3)当点M在直线CD上移动时,∠MPN的大小不变,都是45°.
C组(综合题)
19.对于平面内的∠M和∠N,若存在一个常数k>0,使得∠M+k∠N=360°,则称∠N为∠M的k系补周角.如若∠M=90°,∠N=45°,则∠N为∠M的6系补周角.
(1)若∠H=120°,则∠H的4系补周角的度数为60°.
(2)在平面内AB∥CD,点E是平面内一点,连接BE,DE.
①如图1,∠D=60°,若∠B是∠BED的3系补周角,求∠B的度数;
②如图2,∠ABE和∠CDE均为钝角,点F在点E的右侧,且满足∠ABF=n∠ABE,∠CDF=n∠CDE(其中n为常数,且n>1),点P是∠ABE角平分线BG上的一个动点,在P点运动过程中,请你确定一个点P的位置,使得∠BPD是∠F的k系补周角,并直接写出此时的k值(用含n的式子表示).
解:(2)①过E作EF∥AB,
∴∠B=∠BEF.
∵AB∥CD,
∴EF∥CD.
∴∠D=∠DEF=60°.
∵∠B+60°=∠BEF+∠DEF,
∴∠B+60°=∠BED.
∵∠B是∠BED的3系补周角,
∴∠BED=360°-3∠B.
∴∠B+60°=360°-3∠B.
∴∠B=75°.
②当BG上的动点P为∠CDE的角平分线与BG的交点时,满足∠BPD是∠F的k系补周角,此时k=2n.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
