2021-2022学年北京课改新版八年级上册数学《第12章 三角形》单元测试卷(word解析版)
文档属性
| 名称 | 2021-2022学年北京课改新版八年级上册数学《第12章 三角形》单元测试卷(word解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 181.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-18 17:29:54 | ||
图片预览


文档简介
2021-2022学年北京课改新版八年级上册数学《第12章
三角形》单元测试卷
一.选择题
1.线段BC上有3个点P1、P2、P3,直线BC外有一点A,把A和B、P1、P2、P3、C连接起来,可以得到的三角形个数为( )
A.8个
B.10个
C.12个
D.20个
2.图中三角形的个数是( )
A.8
B.9
C.10
D.11
3.下列图形中有稳定性的是( )
A.正方形
B.直角三角形
C.长方形
D.平行四边形
4.下列长方形中,能使图形不易变形的是( )
A.
B.
C.
D.
5.三角形的重心是( )
A.三角形三条角平分线的交点
B.三角形三条中线的交点
C.三角形三条高所在直线的交点
D.三角形三条边的垂直平分线的交点
6.已知三角形三边分别为2,a﹣1,4,那么a的取值范围是( )
A.1<a<5
B.2<a<6
C.3<a<7
D.4<a<6
7.若△ABC中,∠A:∠B:∠C=1:2:3,则△ABC一定是( )
A.锐角三角形
B.钝角三角形
C.直角三角形
D.任意三角形
8.把三角形的面积分为相等的两部分的是( )
A.三角形的角平分线
B.三角形的中线
C.三角形的高
D.以上都不对
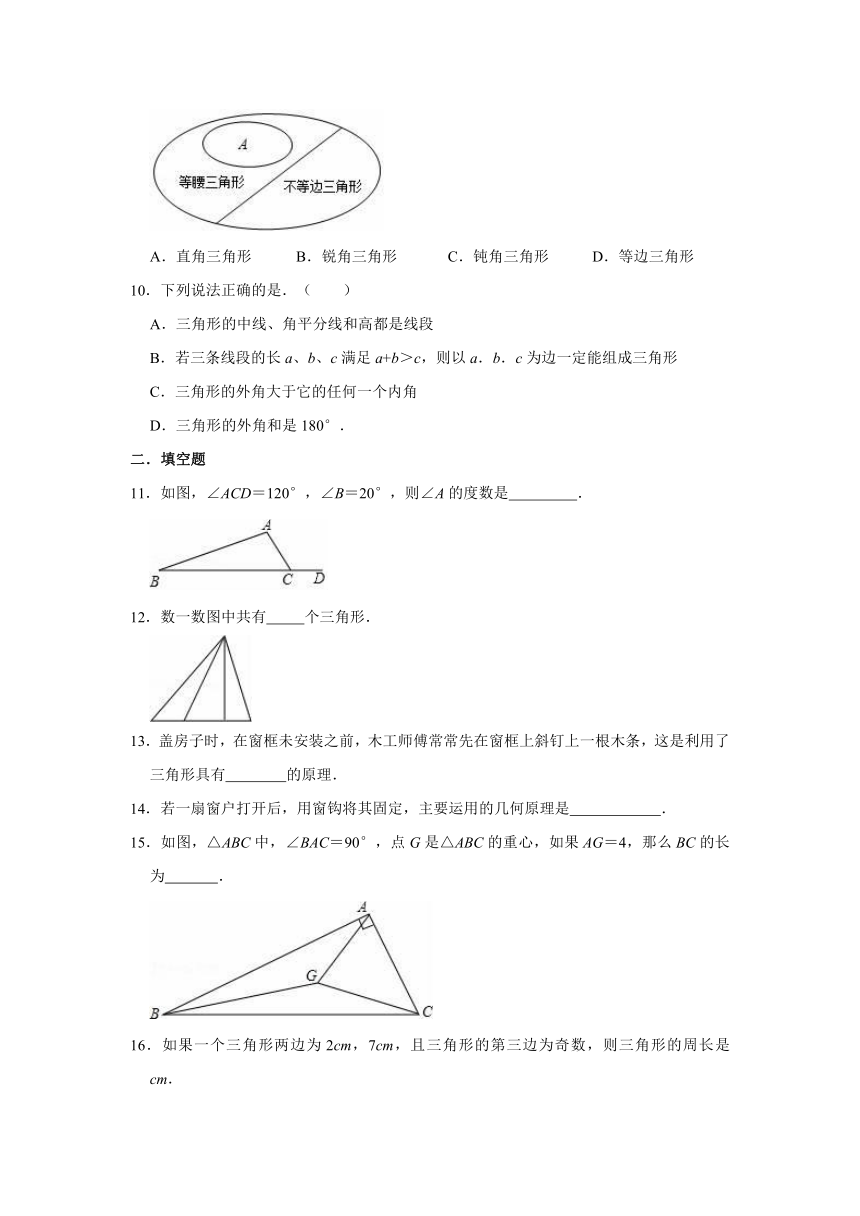
9.三角形按边分类可以用集合来表示,如图所示,图中小椭圆圈里的A表示( )
A.直角三角形
B.锐角三角形
C.钝角三角形
D.等边三角形
10.下列说法正确的是.( )
A.三角形的中线、角平分线和高都是线段
B.若三条线段的长a、b、c满足a+b>c,则以a.b.c为边一定能组成三角形
C.三角形的外角大于它的任何一个内角
D.三角形的外角和是180°.
二.填空题
11.如图,∠ACD=120°,∠B=20°,则∠A的度数是
.
12.数一数图中共有
个三角形.
13.盖房子时,在窗框未安装之前,木工师傅常常先在窗框上斜钉上一根木条,这是利用了三角形具有
的原理.
14.若一扇窗户打开后,用窗钩将其固定,主要运用的几何原理是
.
15.如图,△ABC中,∠BAC=90°,点G是△ABC的重心,如果AG=4,那么BC的长为
.
16.如果一个三角形两边为2cm,7cm,且三角形的第三边为奇数,则三角形的周长是
cm.
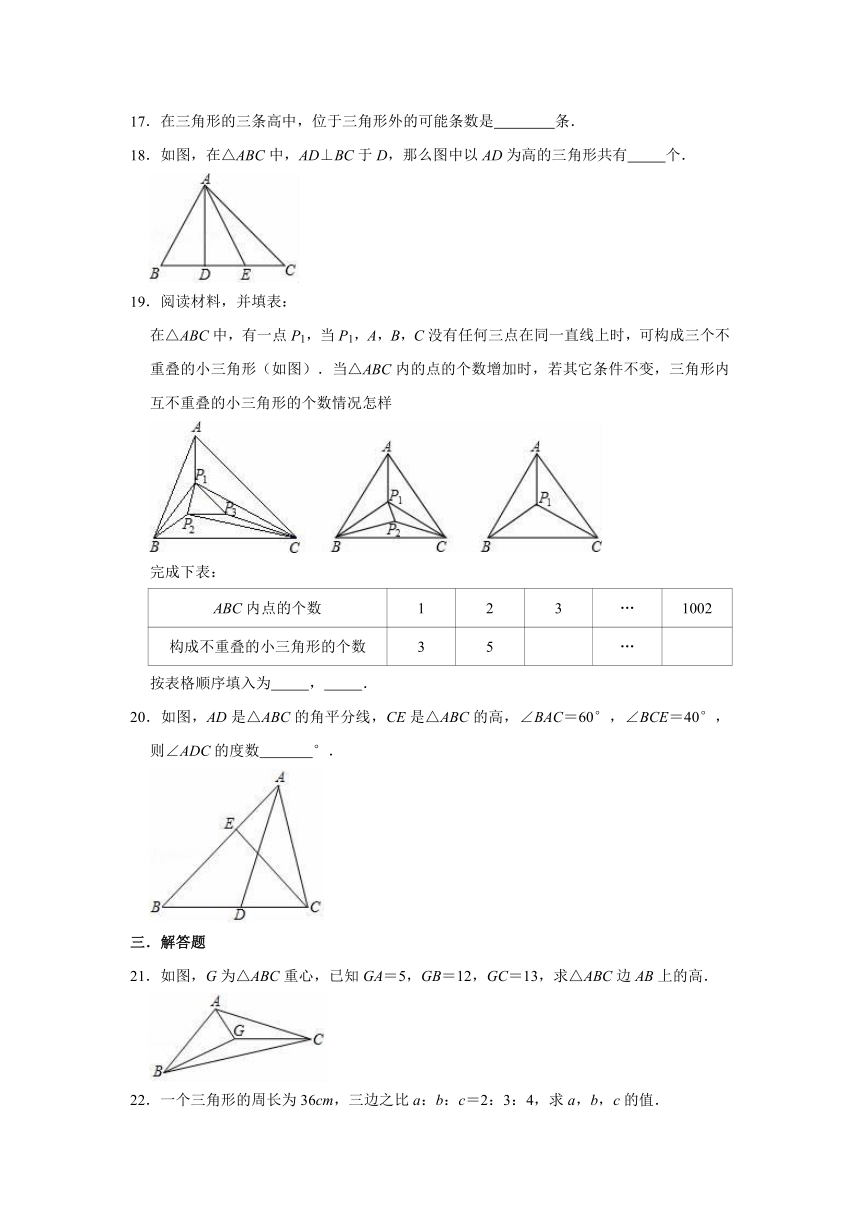
17.在三角形的三条高中,位于三角形外的可能条数是
条.
18.如图,在△ABC中,AD⊥BC于D,那么图中以AD为高的三角形共有
个.
19.阅读材料,并填表:
在△ABC中,有一点P1,当P1,A,B,C没有任何三点在同一直线上时,可构成三个不重叠的小三角形(如图).当△ABC内的点的个数增加时,若其它条件不变,三角形内互不重叠的小三角形的个数情况怎样
完成下表:
ABC内点的个数
1
2
3
…
1002
构成不重叠的小三角形的个数
3
5
…
按表格顺序填入为
,
.
20.如图,AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=40°,则∠ADC的度数
°.
三.解答题
21.如图,G为△ABC重心,已知GA=5,GB=12,GC=13,求△ABC边AB上的高.
22.一个三角形的周长为36cm,三边之比a:b:c=2:3:4,求a,b,c的值.
23.(1)下列图形中具有稳定性是
;(只填图形序号)
(2)对不具有稳定性的图形,请适当地添加线段,使之具有稳定性.
24.一个三角形有两条边相等,周长为20cm,三角形的一边长6cm,求其他两边长.
25.两条平行直线上各有n个点,用这n对点按如下的规则连接线段;
①平行线之间的点在连线段时,可以有共同的端点,但不能有其它交点;
②符合①要求的线段必须全部画出;
图1展示了当n=1时的情况,此时图中三角形的个数为0;
图2展示了当n=2时的一种情况,此时图中三角形的个数为2;
(1)当n=3时,请在图3中画出使三角形个数最少的图形,此时图中三角形的个数为
个;
(2)试猜想当n对点时,按上述规则画出的图形中,最少有多少个三角形?
(3)当n=2006时,按上述规则画出的图形中,最少有多少个三角形?
26.某木材市场上木棒规格与价格如下表:
规格
1m
2m
3m
4m
5m
6m
价格(元/根)
10
15
20
25
30
35
小明的爷爷要做一个三角形的木架养鱼用,现有两根长度分别为3m和5m的木棒,还需要到某木材市场上购买一根.
(1)有几种规格木棒可供小明的爷爷选择?
(2)选择哪一种规格木棒最省钱?
参考答案与试题解析
一.选择题
1.解:从5个点中,任意选2个点组合,显然有10种情况.
故选:B.
2.解:∵图中的三角形有:△AGD,△ADF,△AEF,△AEC,△ABC,△DGF,△DEF,△CEF,△CEB,
∴共9个三角形.
故选:B.
3.解:直角三角形有稳定性,
故选:B.
4.解:∵四个选项中只有B存在三角形,
∴图形B不易变形.
故选:B.
5.解:A、三角形三条角平分线的交于一点,这一点是三角形的内心;
B、三角形三条中线的交于一点,这一点是三角形的重心;
C、三角形三条高所在直线的交于一点,这一点是三角形的垂心.
D、三角形三边垂直平分线的交于一点,这一点是三角形的外心.
故选:B.
6.解:依题意得:4﹣2<a﹣1<4+2,
即:2<a﹣1<6,
∴3<a<7.
故选:C.
7.解:∵△ABC中,∠A:∠B:∠C=1:2:3,
∴设∠A=x°,∠B=2x°,∠C=3x°,
∵∠A+∠B+∠C=180,
∴x+2x+3x=180°,
∴x=30,
∴∠C=90°,∠A=30°,∠B=60°,
即△ABC是直角三角形,
故选:C.
8.解:把三角形的面积分为相等的两部分的是三角形的中线.
故选:B.
9.解:三角形根据边分类,
∴图中小椭圆圈里的A表示等边三角形.
故选:D.
10.解:A.三角形的中线、角平分线和高都是线段,正确;
B.若三条线段的长a、b、c满足a+b>c,则以a.b.c为边一定能组成三角形,错误;
C.三角形的外角大于它的任何一个内角,错误;
D.三角形的外角和是180°,错误,
故选:A.
二.填空题
11.解:∵∠ACD=∠A+∠B,
∴∠A=∠ACD﹣∠B
=120°﹣20°
=100°.
故答案为100°.
12.解:线段AD上有4个点,
可以与E组成的三角形有×4×(4﹣1)=6个.
故答案是:6.
13.解:盖房子时,在窗框未安装好之前,木工师傅常常先在窗框上斜钉一根木条,这样就构成了三角形,故这样做的数学道理是三角形的稳定性.
故答案为:稳定性.
14.解:一扇窗户打开后,用窗钩将其固定,正好形成三角形的形状,
所以,主要运用的几何原理是三角形的稳定性.
故答案为:三角形的稳定性.
15.解:如图,延长AG交BC于点D.
∵点G是△ABC的重心,AG=4,
∴点D为BC的中点,且AG=2DG=4,
∴DG=2,
∴AD=AG+DG=6,
∵△ABC中,∠BAC=90°,AD是斜边的中线,
∴BC=2AD=12.
故答案为12.
16.解:7﹣2<第三边<7+2?5<第三边<9,这个范围的奇数是7,所以三角形的周长是2+7+7=16(cm).
17.解:∵当三角形为直角三角形和锐角三角形时,没有高在三角形外;而当三角形为钝角三角形时,三角形的高有两条在三角形外,一条在三角形内.
∴三角形的三条高中,在三角形外部的最多有2条.
故答案为:0或2.
18.解:∵AD⊥BC于D,
而图中有一边在直线CB上,且以A为顶点的三角形有6个,
∴以AD为高的三角形有6个.
故答案为:6
19.解:当△ABC内的点的个数是n时,三角形内互不重叠的小三角形的个数2n+1.∴按表格顺序填入为7,2005.
20.解:∵CE⊥AB,
∴∠CEB=90°,
∴∠B=90°﹣∠ECB=90°﹣40°=50°,
∵AD平分∠BAC,
∴∠BAD=∠BAC=30°,
∴∠ADC=∠B+∠BAD=50°+30°=80°,
故答案为80.
三.解答题
21.解:延长AG至E,使GD=DE,作CH⊥AB于点G.
∵G为△ABC重心,
∴AG=2GD=GE,BD=DC.
∴△BGD≌△CED(SAS).
∴∠BGE=∠GEC,EC=BG=12.
∵GC2=EG2+EC2,
∴∠BGE=∠GEC=90°.
∴S△ABD===45,
由勾股定理得
AB===13,
∴S△ABC=2S△ABD=90.
∴CH==.
22.解:设三边长分别为2x,3x,4x,
由题意得,2x+3x+4x=36,
解得:x=4.
则a=2×4=8(cm),
b=3×4=12(cm),
c=4×4=16(cm).
23.解:(1)具有稳定性的是①④⑥三个.
(2)如图所示:
24.解:(1)当6是腰时,底边=20﹣6×2=8cm,即其它两边是6cm,8cm,此时6+6=12,能构成三角形;
(2)当6是底边时,腰=(20﹣6)÷2=7cm,此时能构成三角形,所以其它两边是7cm、7cm.
因此其它两边长分别为7cm,7cm,
综上所述两边长分别为6cm,8cm或7cm,7cm.
25.解:(1)
4个;
(2)当有n对点时,最少可以画2(n﹣1)个三角形;
(3)2×(2006﹣1)=4010个.
答:当n=2006时,最少可以画4010个三角形.
26.解:(1)设第三根木棒的长度为xm,
根据三角形的三边关系可得:5﹣3<x<5+3,
解得2<x<8,
x=3,4,5,6共4种,
∴有4种规格木棒可供小明的爷爷选择;
(2)根据木棒的价格可得选3m最省钱.
三角形》单元测试卷
一.选择题
1.线段BC上有3个点P1、P2、P3,直线BC外有一点A,把A和B、P1、P2、P3、C连接起来,可以得到的三角形个数为( )
A.8个
B.10个
C.12个
D.20个
2.图中三角形的个数是( )
A.8
B.9
C.10
D.11
3.下列图形中有稳定性的是( )
A.正方形
B.直角三角形
C.长方形
D.平行四边形
4.下列长方形中,能使图形不易变形的是( )
A.
B.
C.
D.
5.三角形的重心是( )
A.三角形三条角平分线的交点
B.三角形三条中线的交点
C.三角形三条高所在直线的交点
D.三角形三条边的垂直平分线的交点
6.已知三角形三边分别为2,a﹣1,4,那么a的取值范围是( )
A.1<a<5
B.2<a<6
C.3<a<7
D.4<a<6
7.若△ABC中,∠A:∠B:∠C=1:2:3,则△ABC一定是( )
A.锐角三角形
B.钝角三角形
C.直角三角形
D.任意三角形
8.把三角形的面积分为相等的两部分的是( )
A.三角形的角平分线
B.三角形的中线
C.三角形的高
D.以上都不对
9.三角形按边分类可以用集合来表示,如图所示,图中小椭圆圈里的A表示( )
A.直角三角形
B.锐角三角形
C.钝角三角形
D.等边三角形
10.下列说法正确的是.( )
A.三角形的中线、角平分线和高都是线段
B.若三条线段的长a、b、c满足a+b>c,则以a.b.c为边一定能组成三角形
C.三角形的外角大于它的任何一个内角
D.三角形的外角和是180°.
二.填空题
11.如图,∠ACD=120°,∠B=20°,则∠A的度数是
.
12.数一数图中共有
个三角形.
13.盖房子时,在窗框未安装之前,木工师傅常常先在窗框上斜钉上一根木条,这是利用了三角形具有
的原理.
14.若一扇窗户打开后,用窗钩将其固定,主要运用的几何原理是
.
15.如图,△ABC中,∠BAC=90°,点G是△ABC的重心,如果AG=4,那么BC的长为
.
16.如果一个三角形两边为2cm,7cm,且三角形的第三边为奇数,则三角形的周长是
cm.
17.在三角形的三条高中,位于三角形外的可能条数是
条.
18.如图,在△ABC中,AD⊥BC于D,那么图中以AD为高的三角形共有
个.
19.阅读材料,并填表:
在△ABC中,有一点P1,当P1,A,B,C没有任何三点在同一直线上时,可构成三个不重叠的小三角形(如图).当△ABC内的点的个数增加时,若其它条件不变,三角形内互不重叠的小三角形的个数情况怎样
完成下表:
ABC内点的个数
1
2
3
…
1002
构成不重叠的小三角形的个数
3
5
…
按表格顺序填入为
,
.
20.如图,AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=40°,则∠ADC的度数
°.
三.解答题
21.如图,G为△ABC重心,已知GA=5,GB=12,GC=13,求△ABC边AB上的高.
22.一个三角形的周长为36cm,三边之比a:b:c=2:3:4,求a,b,c的值.
23.(1)下列图形中具有稳定性是
;(只填图形序号)
(2)对不具有稳定性的图形,请适当地添加线段,使之具有稳定性.
24.一个三角形有两条边相等,周长为20cm,三角形的一边长6cm,求其他两边长.
25.两条平行直线上各有n个点,用这n对点按如下的规则连接线段;
①平行线之间的点在连线段时,可以有共同的端点,但不能有其它交点;
②符合①要求的线段必须全部画出;
图1展示了当n=1时的情况,此时图中三角形的个数为0;
图2展示了当n=2时的一种情况,此时图中三角形的个数为2;
(1)当n=3时,请在图3中画出使三角形个数最少的图形,此时图中三角形的个数为
个;
(2)试猜想当n对点时,按上述规则画出的图形中,最少有多少个三角形?
(3)当n=2006时,按上述规则画出的图形中,最少有多少个三角形?
26.某木材市场上木棒规格与价格如下表:
规格
1m
2m
3m
4m
5m
6m
价格(元/根)
10
15
20
25
30
35
小明的爷爷要做一个三角形的木架养鱼用,现有两根长度分别为3m和5m的木棒,还需要到某木材市场上购买一根.
(1)有几种规格木棒可供小明的爷爷选择?
(2)选择哪一种规格木棒最省钱?
参考答案与试题解析
一.选择题
1.解:从5个点中,任意选2个点组合,显然有10种情况.
故选:B.
2.解:∵图中的三角形有:△AGD,△ADF,△AEF,△AEC,△ABC,△DGF,△DEF,△CEF,△CEB,
∴共9个三角形.
故选:B.
3.解:直角三角形有稳定性,
故选:B.
4.解:∵四个选项中只有B存在三角形,
∴图形B不易变形.
故选:B.
5.解:A、三角形三条角平分线的交于一点,这一点是三角形的内心;
B、三角形三条中线的交于一点,这一点是三角形的重心;
C、三角形三条高所在直线的交于一点,这一点是三角形的垂心.
D、三角形三边垂直平分线的交于一点,这一点是三角形的外心.
故选:B.
6.解:依题意得:4﹣2<a﹣1<4+2,
即:2<a﹣1<6,
∴3<a<7.
故选:C.
7.解:∵△ABC中,∠A:∠B:∠C=1:2:3,
∴设∠A=x°,∠B=2x°,∠C=3x°,
∵∠A+∠B+∠C=180,
∴x+2x+3x=180°,
∴x=30,
∴∠C=90°,∠A=30°,∠B=60°,
即△ABC是直角三角形,
故选:C.
8.解:把三角形的面积分为相等的两部分的是三角形的中线.
故选:B.
9.解:三角形根据边分类,
∴图中小椭圆圈里的A表示等边三角形.
故选:D.
10.解:A.三角形的中线、角平分线和高都是线段,正确;
B.若三条线段的长a、b、c满足a+b>c,则以a.b.c为边一定能组成三角形,错误;
C.三角形的外角大于它的任何一个内角,错误;
D.三角形的外角和是180°,错误,
故选:A.
二.填空题
11.解:∵∠ACD=∠A+∠B,
∴∠A=∠ACD﹣∠B
=120°﹣20°
=100°.
故答案为100°.
12.解:线段AD上有4个点,
可以与E组成的三角形有×4×(4﹣1)=6个.
故答案是:6.
13.解:盖房子时,在窗框未安装好之前,木工师傅常常先在窗框上斜钉一根木条,这样就构成了三角形,故这样做的数学道理是三角形的稳定性.
故答案为:稳定性.
14.解:一扇窗户打开后,用窗钩将其固定,正好形成三角形的形状,
所以,主要运用的几何原理是三角形的稳定性.
故答案为:三角形的稳定性.
15.解:如图,延长AG交BC于点D.
∵点G是△ABC的重心,AG=4,
∴点D为BC的中点,且AG=2DG=4,
∴DG=2,
∴AD=AG+DG=6,
∵△ABC中,∠BAC=90°,AD是斜边的中线,
∴BC=2AD=12.
故答案为12.
16.解:7﹣2<第三边<7+2?5<第三边<9,这个范围的奇数是7,所以三角形的周长是2+7+7=16(cm).
17.解:∵当三角形为直角三角形和锐角三角形时,没有高在三角形外;而当三角形为钝角三角形时,三角形的高有两条在三角形外,一条在三角形内.
∴三角形的三条高中,在三角形外部的最多有2条.
故答案为:0或2.
18.解:∵AD⊥BC于D,
而图中有一边在直线CB上,且以A为顶点的三角形有6个,
∴以AD为高的三角形有6个.
故答案为:6
19.解:当△ABC内的点的个数是n时,三角形内互不重叠的小三角形的个数2n+1.∴按表格顺序填入为7,2005.
20.解:∵CE⊥AB,
∴∠CEB=90°,
∴∠B=90°﹣∠ECB=90°﹣40°=50°,
∵AD平分∠BAC,
∴∠BAD=∠BAC=30°,
∴∠ADC=∠B+∠BAD=50°+30°=80°,
故答案为80.
三.解答题
21.解:延长AG至E,使GD=DE,作CH⊥AB于点G.
∵G为△ABC重心,
∴AG=2GD=GE,BD=DC.
∴△BGD≌△CED(SAS).
∴∠BGE=∠GEC,EC=BG=12.
∵GC2=EG2+EC2,
∴∠BGE=∠GEC=90°.
∴S△ABD===45,
由勾股定理得
AB===13,
∴S△ABC=2S△ABD=90.
∴CH==.
22.解:设三边长分别为2x,3x,4x,
由题意得,2x+3x+4x=36,
解得:x=4.
则a=2×4=8(cm),
b=3×4=12(cm),
c=4×4=16(cm).
23.解:(1)具有稳定性的是①④⑥三个.
(2)如图所示:
24.解:(1)当6是腰时,底边=20﹣6×2=8cm,即其它两边是6cm,8cm,此时6+6=12,能构成三角形;
(2)当6是底边时,腰=(20﹣6)÷2=7cm,此时能构成三角形,所以其它两边是7cm、7cm.
因此其它两边长分别为7cm,7cm,
综上所述两边长分别为6cm,8cm或7cm,7cm.
25.解:(1)
4个;
(2)当有n对点时,最少可以画2(n﹣1)个三角形;
(3)2×(2006﹣1)=4010个.
答:当n=2006时,最少可以画4010个三角形.
26.解:(1)设第三根木棒的长度为xm,
根据三角形的三边关系可得:5﹣3<x<5+3,
解得2<x<8,
x=3,4,5,6共4种,
∴有4种规格木棒可供小明的爷爷选择;
(2)根据木棒的价格可得选3m最省钱.
同课章节目录
- 第十章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的乘除法
- 10.4 分式的加减法
- 10.5 可化为一元一次方程的分式方程及其应用
- 第十一章 实数和二次根式
- 11.1 平方根
- 11.2 立方根
- 11.3 用科学计算器开方
- 11.4 无理数与实数
- 11.5 二次根式及其性质
- 11.6 二次根式的乘除法
- 11.7 二次根式的加减法
- 第十二章 三角形
- 12.1 三角形
- 12.2 三角形的性质
- 12.3 三角形中的主要线段
- 12.4 全等三角形
- 12.5 全等三角形的判定
- 12.6 等腰三角形
- 12.7 直角三角形
- 12.8 基本作图
- 12.9 逆命题 、逆定理
- 12.10 轴对称和轴对称图形
- 12.11 勾股定理
- 12.12 勾股定理的逆定理
- 第十三章 事件与可能性
- 13.1 必然事件与随机事件
- 13.2 随机事件发生的可能性
- 13.3 求简单随机事件发生的可能性的大小
