正多边形和圆

(共23张PPT)
A
B
C
D
E
24.3 正多边形和圆(1)
观察下列图形他们有什么特点？
各边相等,各角也相等的多边形叫做 正多边形.
三条边相等，三个角相等（60度）。
四条边相等，四个角相等（900）。
正三角形
正方形
一 .正多边形定义
如果一个正多边形有n条边，那么这个正多边形 叫做正n边形。
思考: 菱形是正多边形吗 矩形是正多边形呢
菱形, 矩形都不是正多边形
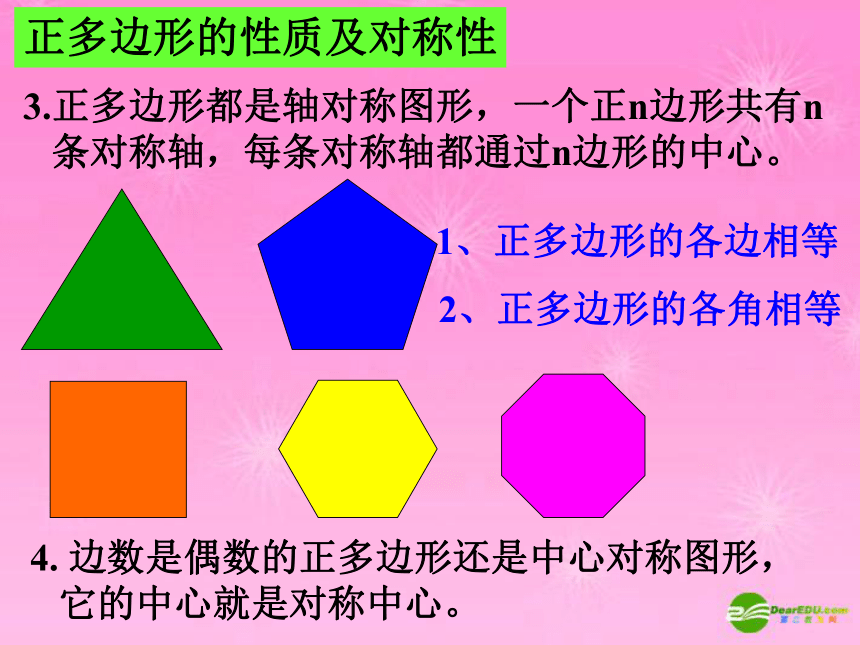
3.正多边形都是轴对称图形，一个正n边形共有n
条对称轴，每条对称轴都通过n边形的中心。
正多边形的性质及对称性
4. 边数是偶数的正多边形还是中心对称图形，
它的中心就是对称中心。
1、正多边形的各边相等
2、正多边形的各角相等
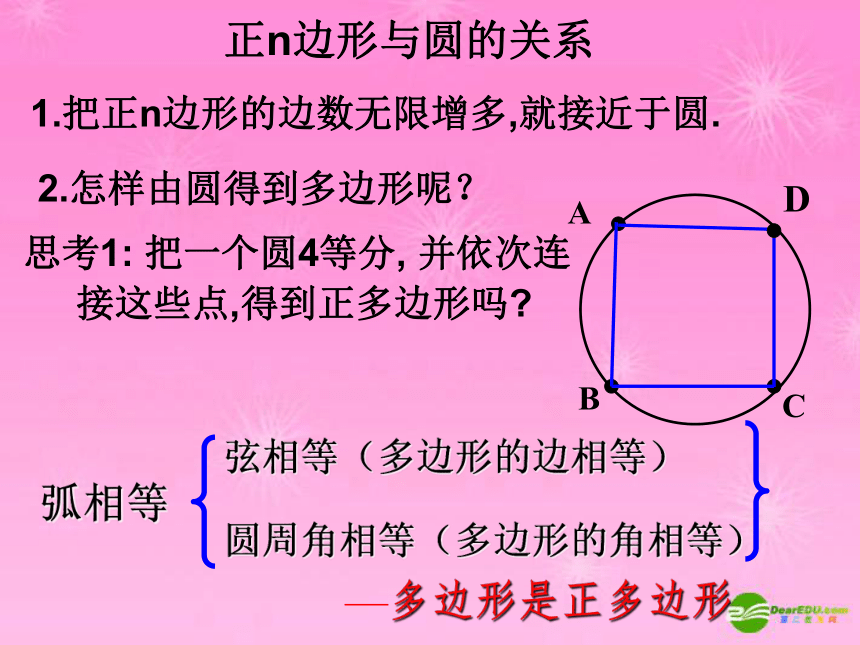
正n边形与圆的关系
1.把正n边形的边数无限增多,就接近于圆.
2.怎样由圆得到多边形呢？
A
B
C
D
思考1: 把一个圆4等分, 并依次连
接这些点,得到正多边形吗
弧相等
弦相等（多边形的边相等）
圆周角相等（多边形的角相等）
—多边形是正多边形
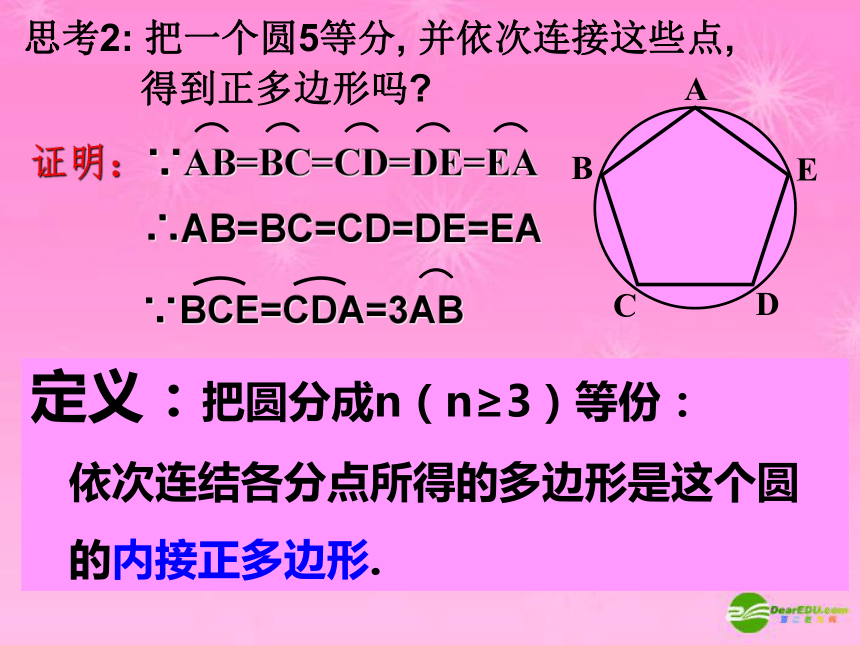
思考2: 把一个圆5等分, 并依次连接这些点,
得到正多边形吗
证明：∵AB=BC=CD=DE=EA
A
B
C
D
E
⌒
⌒
⌒
⌒
⌒
∴AB=BC=CD=DE=EA
∵BCE=CDA=3AB
⌒
∴∠A=∠B
同理∠B=∠C=∠D=∠E
∴∠A=∠B=∠C=∠D=∠E
又∵顶点A、B、C、D、E都在⊙O上
∴五边形ABCDE是⊙O的 内接正五边形.
定义：把圆分成n（n≥3）等份：
依次连结各分点所得的多边形是这个圆
的内接正多边形.
E
F
C
D
.
O
中心角
半径R
边心距r
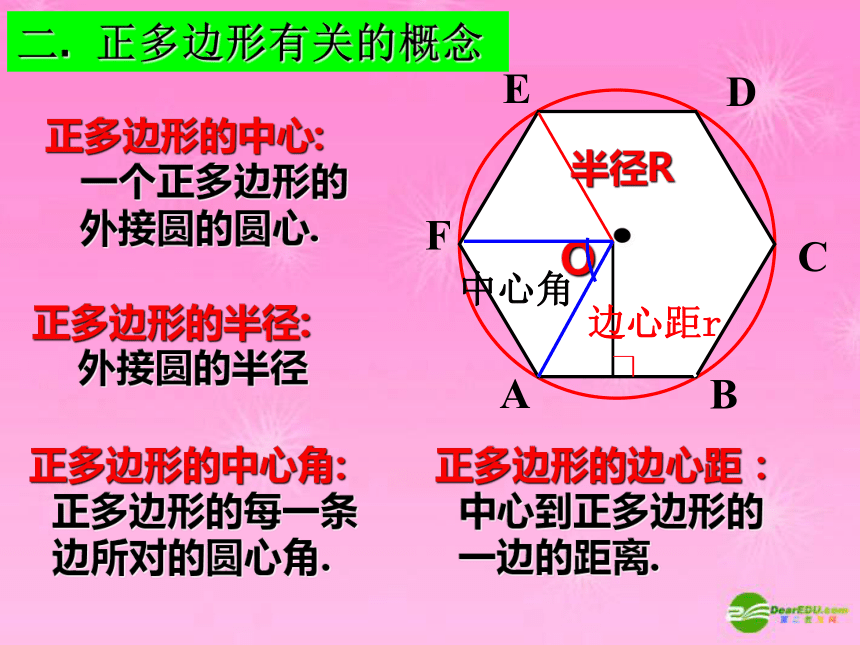
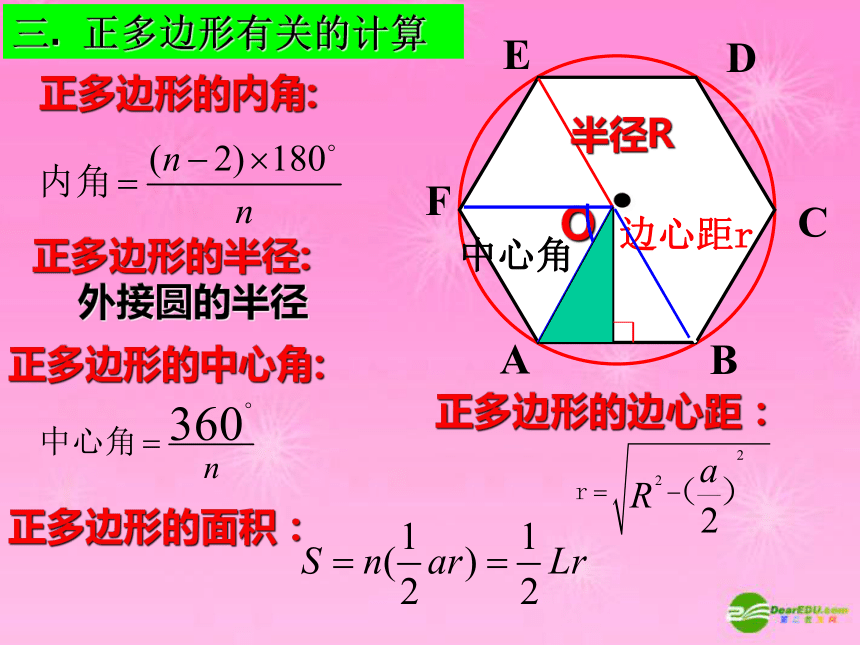
正多边形的中心:
一个正多边形的
外接圆的圆心.
正多边形的半径:
外接圆的半径
正多边形的中心角:
正多边形的每一条
边所对的圆心角.
正多边形的边心距：
中心到正多边形的
一边的距离.
二. 正多边形有关的概念
A
B
E
F
C
D
.
O
中心角
半径R
边心距r
正多边形的内角:
正多边形的半径:
外接圆的半径
正多边形的中心角:
正多边形的边心距：
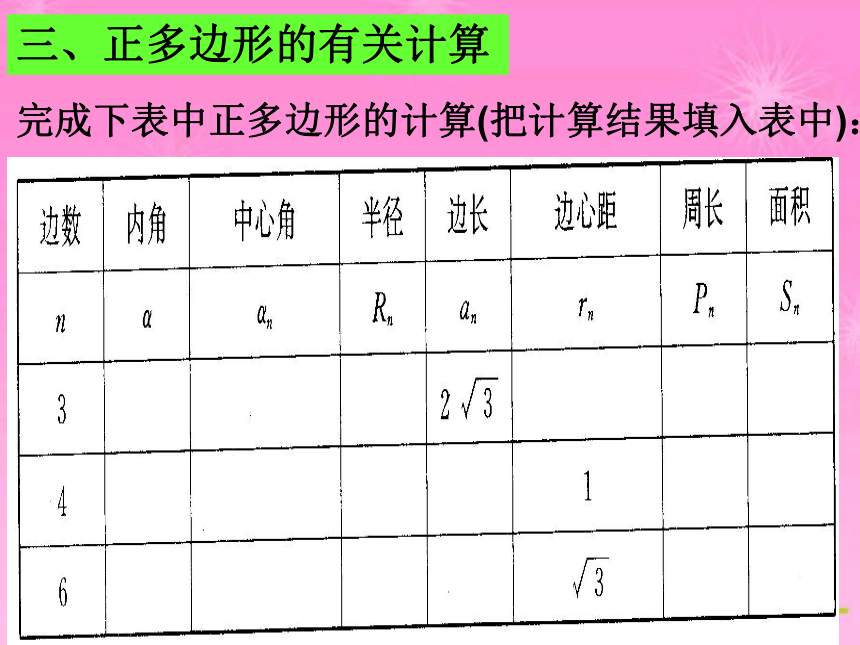
三. 正多边形有关的计算
A
B
正多边形的面积：
完成下表中正多边形的计算(把计算结果填入表中)：
三、正多边形的有关计算
例 有一个亭子它的地基是半径为4m的正六边形,
求地基的周长和面积(精确到0.1平方米).
F
A
D
E
.
.
O
B
C
r
R
P
∴亭子的周长 L=6×4=24(m)
F
A
D
E
.
.
O
B
C
r
R=4
P
例2:如图,M,N分别是⊙O内接正多边形AB,BC上的点,且BM=CN.
(1)求图①中∠MON的度数;
(2)图②中∠MON= ;
图③中∠MON= ;
(3)试探究∠MON的度数与正n边形的边数n的关系.
A
B
C
D
E
A
B
C
D
.
.
.
A
B
C
M
N
M
N
M
N
O
O
O
1、正八边形的中心角是 度;它的外角是
度.
2．圆内接正方形的半径与边长的比值是________
3．正多边形的边心距与边长之比为 :2,则此多边形的边数是 .
4．已知圆内接正方形的边长为2，则该圆的内接正六边形边长为__________．
5． 圆内接正六边形的边长是8 cm用么该正六边形的半径为________；边心距为________．
四.拓展练习
6．以下有四种说法：①顺次连结对角线相等的四边形各边中点，则所得的四边形是菱形；②等边三角形是轴对称图形，但不是中心对称图形；③顶点在圆周上的角是圆周角；④边数相同的正多边形都相似，其中正确的有（ ）
A．1个 B．2个 C．3个 D 4个
7．正多边形的中心角与该正多边形一个内角的关系是（ ）
A.互余 B.互补 C.互余或互补 D.不能确定
9．若一个正多边形的每一个外角都等于36°,那么这个正多边形的中心角为（ ）
A．36° B、 18°
C．72° D．54°
10．将一个边长为a正方形硬纸片剪去四角，使它成为正n边形，那么正n边形的面积为（ ）
11．正六边形螺帽的边长为a，那么扳手的开口b最小应是( )
A、
1、判断题。
①各边都相等的多边形是正多边形。 （ ）
②一个圆有且只有一个内接正多边形 （ ）
2、证明题。
求证：顺次连结正六边形
各边中点所得的多
边形是正六边形。
A
B
C
D
E
F
×
×
A
B
C
D
E
3.求证：正五边形的对角线相等。
证明： 在△BCD和△CDE中
∵BC=CD
∠BCD=∠CDE
CD=DE
∴△BCD≌△CDE
∴BD=CE
同理可证对角线相等。
已知：ABCDE是正五边形，求证：DB=CE
1、怎样判定一个多边形是正多边形？
①各边相等
②各角相等
的多边形叫做正多边形。
E
F
C
D
.
O
中心角
半径R
边心距r
正多边形的中心:
一个正多边形的
外接圆的圆心.
正多边形的半径:
外接圆的半径
正多边形的中心角:
正多边形的每一条
边所对的圆心角.
正多边形的边心距：
中心到正多边形的
一边的距离.
2. 正多边形有关的概念
A
B
E
F
C
D
.
O
中心角
半径R
边心距r
正多边形的内角:
正多边形的半径:
外接圆的半径
正多边形的中心角:
正多边形的边心距：
3. 正多边形有关的计算
A
B
正多边形的面积：
练习：
P105
P107
作业：
基础题 P108 第5题
拔高题 P108 第6题
又∵五边形PQRST的各边都与⊙O相切，
∴五边形PQRST的是O外切正五边形。
证明：连结OA、OB、OC，则：
∠OAB=∠OBA=∠OBC=∠OCB
∵TP、PQ、QR分别是以A、B、C
为切点的⊙O的切线
∴∠OAP=∠OBP=∠OBQ=∠OCQ
∴∠PAB=∠PBA=∠QBC=∠QCB
又∵AB=BC
∴AB=BC
∴△PAB与△QBC是全等
的等腰三角形。
∴∠P=∠Q PQ=2PA
同理∠Q=∠R=∠S=∠T
QR=RS=ST=TP=2PA
⌒
⌒
A
B
C
D
E
P
Q
R
S
T
O
定义：经过各分点作圆的切线，以相邻切
线的交点为顶点的多边形是这个圆的
外切正多边形.
思考3: 过圆的5等份点画圆的切线, 则以相邻切
线的交点为顶点的多边形是正多边形吗