镶嵌
图片预览







文档简介
(共34张PPT)
好漂亮的地板!这是怎么铺设的 一点空隙也没有.
我们经常能见到各种建筑物的地板,观察地板,就能发现地板常用各种多边形地砖铺砌成美丽的图案
7.4 课题学习 镶嵌
用一些形状、大小完全相同的一种或几种平面图形进行拼接,彼此之间不留空隙,不重叠地把平面的一部分完全覆盖,这就是平面图形的镶嵌.
不留空隙
不重叠
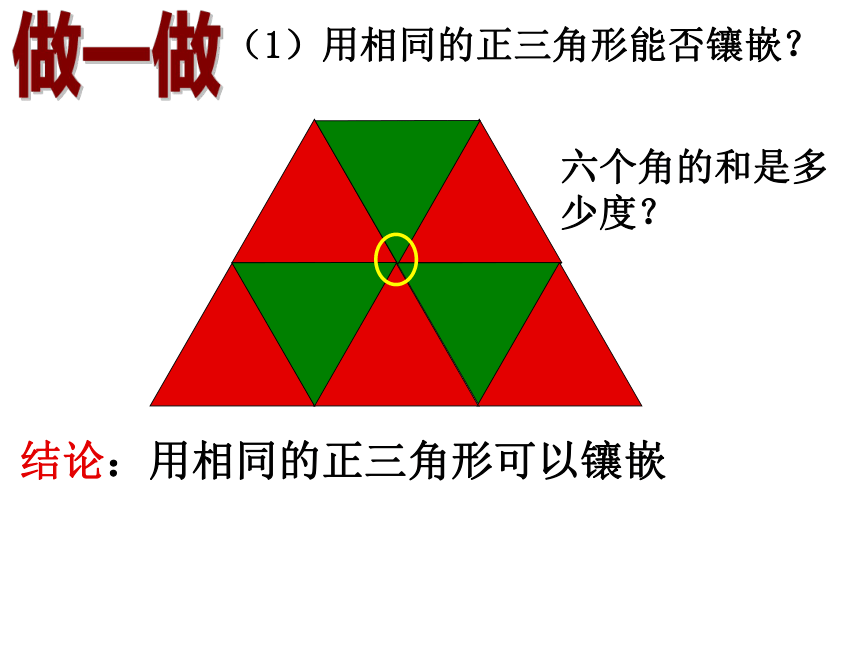
(1)用相同的正三角形能否镶嵌?
结论:用相同的正三角形可以镶嵌
六个角的和是多少度?
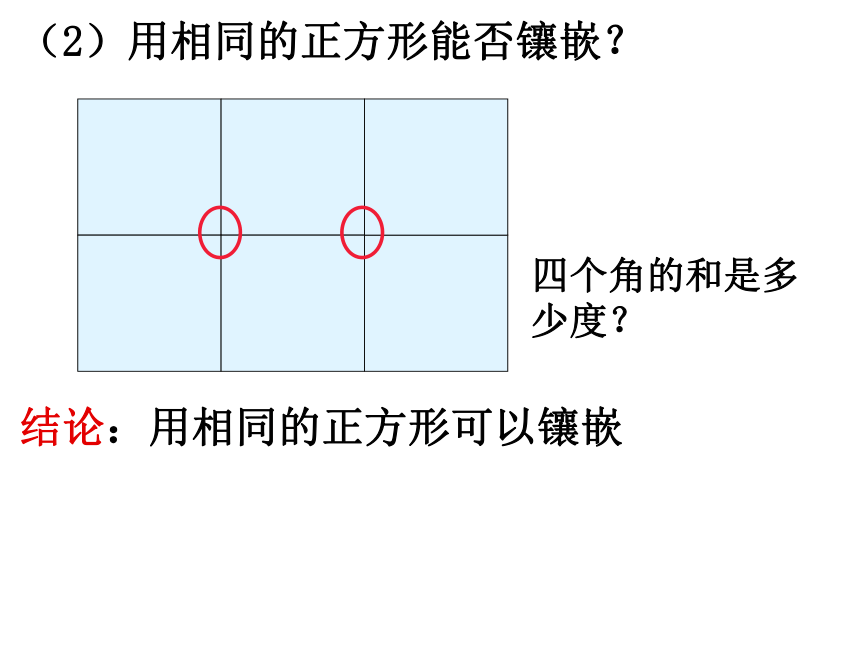
(2)用相同的正方形能否镶嵌?
结论:用相同的正方形可以镶嵌
四个角的和是多少度?
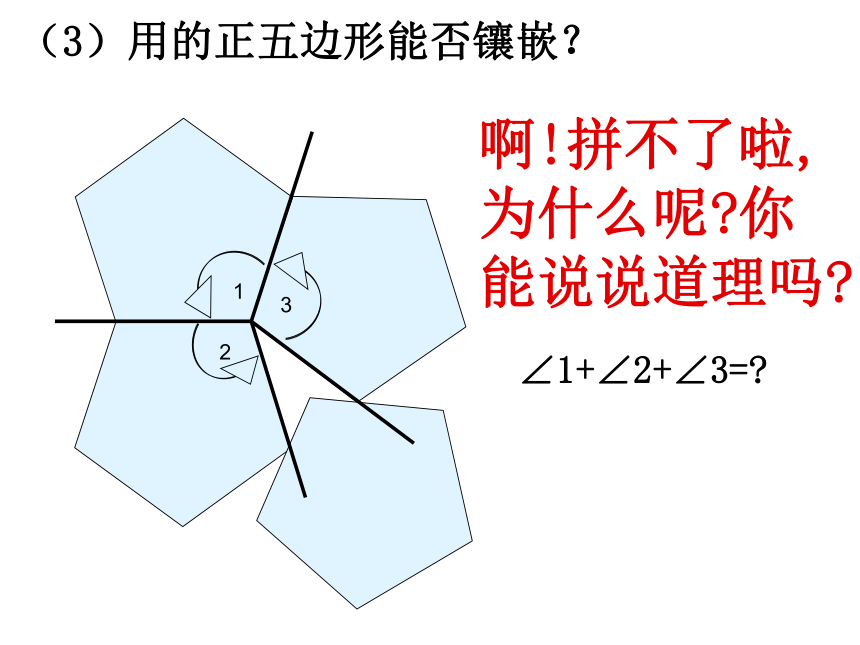
啊!拼不了啦,为什么呢 你能说说道理吗
1
2
3
∠1+∠2+∠3=
(3)用的正五边形能否镶嵌?
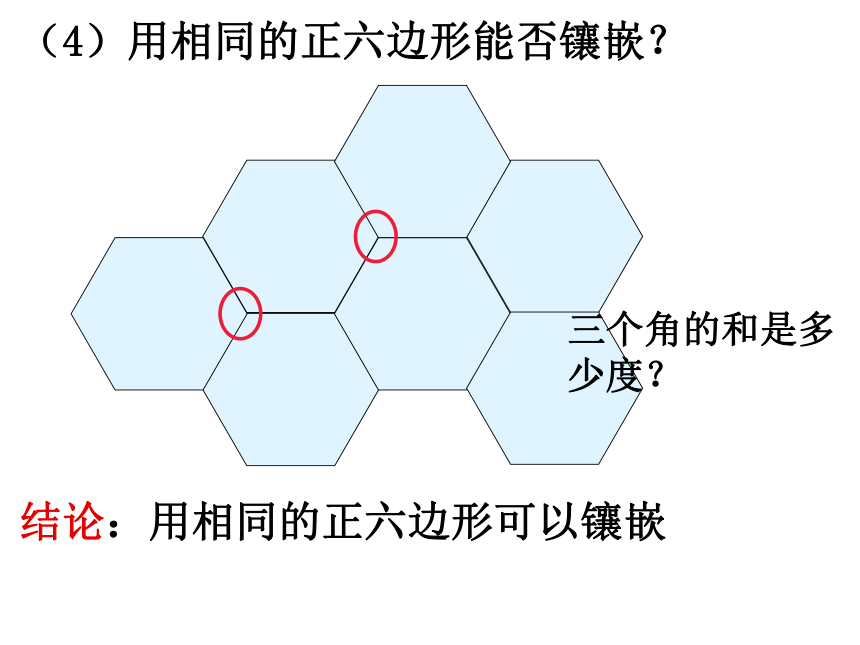
(4)用相同的正六边形能否镶嵌?
结论:用相同的正六边形可以镶嵌
三个角的和是多少度?
要不留空隙、不重叠地镶嵌一个平面,需使得拼接点处的各角之和360°.
镶嵌需要满足什么条件?
你还能找到能镶嵌的其他正多边形吗?
在正多边形里只用单独一种正多边形进行镶嵌:只有正三角形、正四边形、正六边形可以镶嵌,而其他的正多边形不可单独一种进行镶嵌.
我们可以利用多边形设计一些美丽的图案
探究
用同一种平面图形如果不能镶嵌,用两种或者两种以上平面图形能不能镶嵌呢
正多边形边数 3 4 5 6 8 9 10 12
每个内角度数
60°
90°
108°
120°
135°
140°
144°
150°
3,4
4,8
5,10
3,12
4,6,12
3,6
正多边形边数 3 4 5 6 8 9 10 12
每个内角度数
60°
90°
108°
120°
135°
140°
144°
150°
正四和正三
正多边形边数 3 4 5 6 8 9 10 12
每个内角度数
60°
90°
108°
120°
135°
140°
144°
150°
正六和正三
正多边形边数 3 4 5 6 8 9 10 12
每个内角度数
60°
90°
108°
120°
135°
140°
144°
150°
正四和正八
正多边形边数 3 4 5 6 8 9 10 12
每个内角度数
60°
90°
108°
120°
135°
140°
144°
150°
正五和正十
正多边形边数 3 4 5 6 8 9 10 12
每个内角度数
60°
90°
108°
120°
135°
140°
144°
150°
正十二和正三
正多边形边数 3 4 5 6 8 9 10 12
每个内角度数
60°
90°
108°
120°
135°
140°
144°
150°
正十二和正六和正四
同一种任意三角形可否镶嵌成一个平面?
同一种任意四边形可否镶嵌成一个平面?
同一种任意三角形、任意四边形可以镶嵌成一个平面!
2
3
课堂小结
1.能镶嵌的条件:使得拼接点处的各角之和为360°.
2.用相同的正三角形或正四边形或正六边形可以镶嵌.
3.用相同的任意三角形或任意四边形可以镶嵌.
4.有时用两种或两种以上的正多边形也可以镶嵌.如正四边形和正八边形,正四边形、正六边形和正十二边形等.
3.如图, 在△ABC中, BD、CE分别平分∠ABC和∠ACB.
(1).若∠A=60°,求∠BOC的度数.
(2).若∠A=α,求∠BOC的度数.
5.如图, 在△ABC中, AO、CO分别平分三角形的外角∠DAC和∠ACE.
(1).若∠B=90°,求∠O的度数.
(2).若∠B=α,求∠O的度数.
6.如图, 在△ABC中, 延长BC至D, BE、CE分别平分∠ABC和∠ACD.
(1).若∠A=80°,求∠E的度数.
(2).根据(1)猜测∠E 与∠A的关系,
并说明理由.
作业:
课本P85 9 10
<全品>课时二十五
好漂亮的地板!这是怎么铺设的 一点空隙也没有.
我们经常能见到各种建筑物的地板,观察地板,就能发现地板常用各种多边形地砖铺砌成美丽的图案
7.4 课题学习 镶嵌
用一些形状、大小完全相同的一种或几种平面图形进行拼接,彼此之间不留空隙,不重叠地把平面的一部分完全覆盖,这就是平面图形的镶嵌.
不留空隙
不重叠
(1)用相同的正三角形能否镶嵌?
结论:用相同的正三角形可以镶嵌
六个角的和是多少度?
(2)用相同的正方形能否镶嵌?
结论:用相同的正方形可以镶嵌
四个角的和是多少度?
啊!拼不了啦,为什么呢 你能说说道理吗
1
2
3
∠1+∠2+∠3=
(3)用的正五边形能否镶嵌?
(4)用相同的正六边形能否镶嵌?
结论:用相同的正六边形可以镶嵌
三个角的和是多少度?
要不留空隙、不重叠地镶嵌一个平面,需使得拼接点处的各角之和360°.
镶嵌需要满足什么条件?
你还能找到能镶嵌的其他正多边形吗?
在正多边形里只用单独一种正多边形进行镶嵌:只有正三角形、正四边形、正六边形可以镶嵌,而其他的正多边形不可单独一种进行镶嵌.
我们可以利用多边形设计一些美丽的图案
探究
用同一种平面图形如果不能镶嵌,用两种或者两种以上平面图形能不能镶嵌呢
正多边形边数 3 4 5 6 8 9 10 12
每个内角度数
60°
90°
108°
120°
135°
140°
144°
150°
3,4
4,8
5,10
3,12
4,6,12
3,6
正多边形边数 3 4 5 6 8 9 10 12
每个内角度数
60°
90°
108°
120°
135°
140°
144°
150°
正四和正三
正多边形边数 3 4 5 6 8 9 10 12
每个内角度数
60°
90°
108°
120°
135°
140°
144°
150°
正六和正三
正多边形边数 3 4 5 6 8 9 10 12
每个内角度数
60°
90°
108°
120°
135°
140°
144°
150°
正四和正八
正多边形边数 3 4 5 6 8 9 10 12
每个内角度数
60°
90°
108°
120°
135°
140°
144°
150°
正五和正十
正多边形边数 3 4 5 6 8 9 10 12
每个内角度数
60°
90°
108°
120°
135°
140°
144°
150°
正十二和正三
正多边形边数 3 4 5 6 8 9 10 12
每个内角度数
60°
90°
108°
120°
135°
140°
144°
150°
正十二和正六和正四
同一种任意三角形可否镶嵌成一个平面?
同一种任意四边形可否镶嵌成一个平面?
同一种任意三角形、任意四边形可以镶嵌成一个平面!
2
3
课堂小结
1.能镶嵌的条件:使得拼接点处的各角之和为360°.
2.用相同的正三角形或正四边形或正六边形可以镶嵌.
3.用相同的任意三角形或任意四边形可以镶嵌.
4.有时用两种或两种以上的正多边形也可以镶嵌.如正四边形和正八边形,正四边形、正六边形和正十二边形等.
3.如图, 在△ABC中, BD、CE分别平分∠ABC和∠ACB.
(1).若∠A=60°,求∠BOC的度数.
(2).若∠A=α,求∠BOC的度数.
5.如图, 在△ABC中, AO、CO分别平分三角形的外角∠DAC和∠ACE.
(1).若∠B=90°,求∠O的度数.
(2).若∠B=α,求∠O的度数.
6.如图, 在△ABC中, 延长BC至D, BE、CE分别平分∠ABC和∠ACD.
(1).若∠A=80°,求∠E的度数.
(2).根据(1)猜测∠E 与∠A的关系,
并说明理由.
作业:
课本P85 9 10
<全品>课时二十五
