2018-2019学年河北省石家庄二十三中七年级(下)期末数学试卷(word解析版)
文档属性
| 名称 | 2018-2019学年河北省石家庄二十三中七年级(下)期末数学试卷(word解析版) |  | |
| 格式 | doc | ||
| 文件大小 | 327.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-17 21:21:28 | ||
图片预览




文档简介
2018-2019学年河北省石家庄二十三中七年级(下)期末数学试卷
一、选择题(16个小题,1-10小题各3分,11-16小题各2分,共42分)
1.(3分)把58000表示成a×10n(其中1≤a≤10,n为整数)的形式,则n=( )
A.﹣4 B.2 C.3 D.4
2.(3分)如图,∠3的同位角是( )
A.∠1 B.∠2 C.∠B D.∠C
3.(3分)下列等式从左到右的变形是因式分解的是( )
A.12a2b=3a?4ab B.ax﹣ay=a(x﹣y)
C.(x+2)(x﹣3)=x2﹣9 D.4x2+8x﹣1=4x(x+2)﹣1
4.(3分)如图,已知直线AB与CD平行,直线EF与AB,CD分别交于点E,F,若∠1=125°,则∠2=( )
A.65° B.55° C.50° D.45°
5.(3分)下列各式中,计算结果为a8的是( )
A.a4+a4 B.a16÷a2 C.a4?a4 D.(﹣2a4)2
6.(3分)若一个三角形两边长分别是5cm和8cm,则第三边长可能是( )
A.14cm B.13cm C.10cm D.﹣3cm
7.(3分)如图是测量嘉琪跳远成绩的示意图,直线l是起跳线,以下线段的长度能作为嘉琪跳远成绩的是( )
A.BP B.CP C.AP D.AO
8.(3分)解方程组,如果用加减消元法消去n,那么下列方法可行的是( )
A.①×4+②×3 B.①×4﹣②×3 C.①×3﹣②×4 D.①×3+②×4
9.(3分)一副三角板如图放置,点D在CB的延长线上,EF∥CD,∠C=∠EDF=90°,∠A=45°,∠EFD=30°,则∠DFB=( )
A.15° B.20° C.25° D.30°
10.(3分)下列命题:
①对顶角相等;②内错角相等;
③两条平行线之间的距离处处相等;
④有且只有一条直线垂直于已知直线.
其中是假命题的有( )
A.①② B.②④ C.②③ D.③④
11.(2分)如图,已知有理数a,b,c在数轴上对应的点分别为A,B,C,则下列不等式中不正确的是( )
A.c<b<a B.ac>ab C.cb>ab D.c+b<a+b
12.(2分)若x2﹣4x﹣1=0,则代数式2x(x﹣3)﹣(x﹣1)2+3的值为( )
A.3 B.4 C.1 D.0
13.(2分)若关于x的不等式组的解集为x>3,那么a的取值范围是( )
A.a>3 B.a<3 C.a≥3 D.a≤3
14.(2分)如(x+m)与(x+3)的乘积中不含x的一次项,则m的值为( )
A.﹣3 B.3 C.0 D.1
15.(2分)在锐角三角形ABC中,∠A=50°,则∠B的范围是( )
A.0°<∠B<90° B.40°<∠B<130°
C.40°≤∠B≤90° D.40°<∠B<90°
16.(2分)如图,在长方形ABCD中,AB=5,第一次平移将长方形ABCD沿AB方向向右平移4个单位长度,得到长方形A1B1C1D1,第二次平移将长方形A1B1C1D1沿A1B1方向向右平移4个单位长度,得到长方形A2B2C2D2,……,第n次平移将长方形An﹣1Bn﹣1Cn﹣1Dn﹣1沿An﹣1Bn﹣1方向向右平移4个单位长度,得到长方形AnBn?nDn(n>2).若ABn的长为45,则n=( )
A.10 B.11 C.16 D.9
二、填空题(共12分,每小题各3分)
17.(3分)已知关于x,y的二元一次方程mx﹣2y=2的一组解为,则m= .
18.(3分)若有理数a,b满足|a+|+b2=0,则ab= .
19.(3分)分解因式:x3y﹣2x2y+xy= .
20.(3分)在如图所示的长方形中放置了8个形状、大小都相同的小长方形,则图中阴影部分的面积为 .
三、解答题(共6个小题,共46分)
21.(12分)计算:
(1)解方程组:;
(2)解不等式组,并把解集在数轴上表示出来.
(3)已知:(x+1)(x+2)﹣ =6x+2,请计算 内应填写的式子.
22.(5分)在多项式的乘法公式中,完全平方公式是其中重要的一个.
(1)请你补全完全平方公式的推导过程:
(a+b)2=(a+b)(a+b)=a2+ + +b2=a2+ +b2
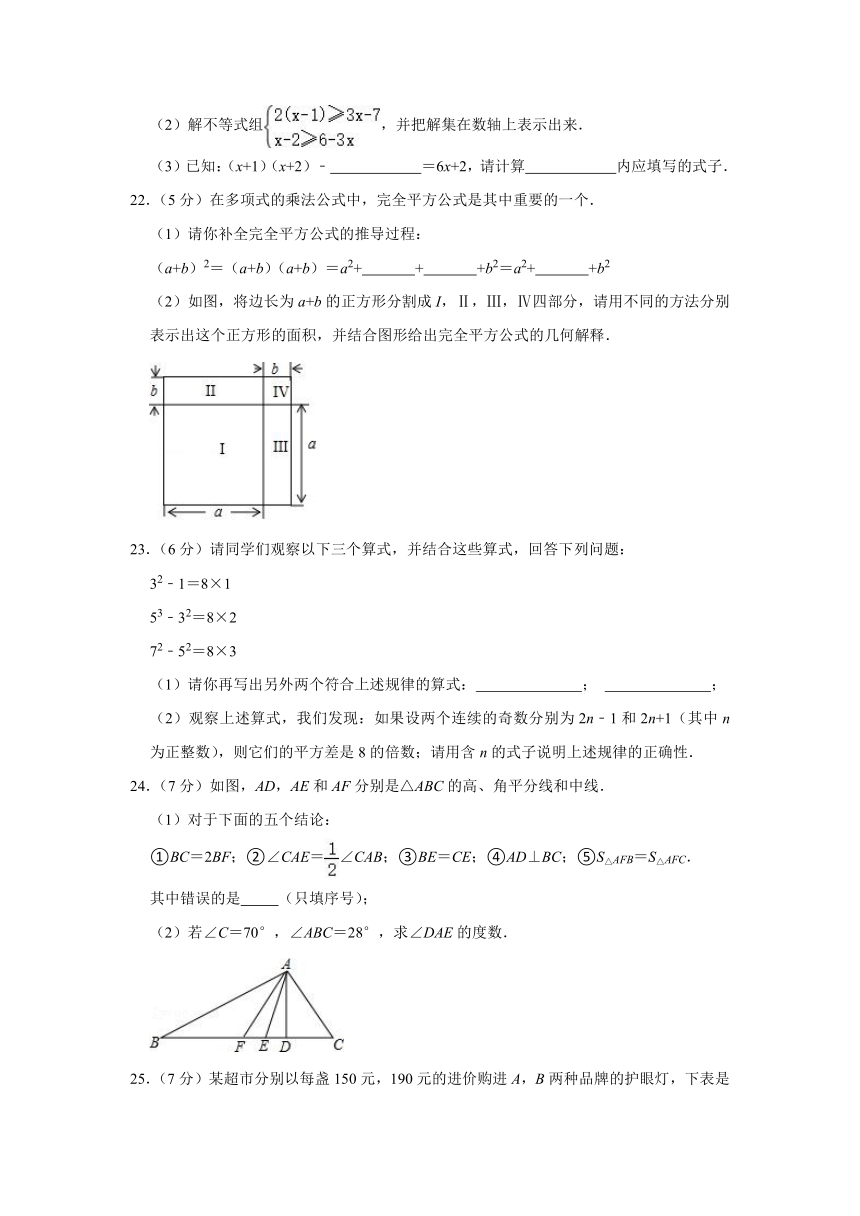
(2)如图,将边长为a+b的正方形分割成I,Ⅱ,Ⅲ,Ⅳ四部分,请用不同的方法分别表示出这个正方形的面积,并结合图形给出完全平方公式的几何解释.
23.(6分)请同学们观察以下三个算式,并结合这些算式,回答下列问题:
32﹣1=8×1
53﹣32=8×2
72﹣52=8×3
(1)请你再写出另外两个符合上述规律的算式: ; ;
(2)观察上述算式,我们发现:如果设两个连续的奇数分别为2n﹣1和2n+1(其中n为正整数),则它们的平方差是8的倍数;请用含n的式子说明上述规律的正确性.
24.(7分)如图,AD,AE和AF分别是△ABC的高、角平分线和中线.
(1)对于下面的五个结论:
①BC=2BF;②∠CAE=∠CAB;③BE=CE;④AD⊥BC;⑤S△AFB=S△AFC.
其中错误的是 (只填序号);
(2)若∠C=70°,∠ABC=28°,求∠DAE的度数.
25.(7分)某超市分别以每盏150元,190元的进价购进A,B两种品牌的护眼灯,下表是近两天的销售情况.
销售日期 销售数量(盏) 销售收入(元)
A品牌 B品牌
第一天 2 1 680
第二天 3 4 1670
(1)求A,B两种品牌护眼灯的销售价;
(2)若超市准备用不超过4900元的金额购进这两种品牌的护眼灯共30盏,求B品牌的护眼灯最多采购多少盏?
26.(9分)问题解决:如图1,已知AB∥CD,E是直线AB,CD内部一点,连接BE,DE,若∠ABE=40°,∠CDE=60°,求∠BED的度数.
嘉琪想到了如图2所示的方法,但是没有解答完,下面是嘉淇未完成的解答过程:
解:过点E作EF∥AB,
∴∠ABE=∠BEF=40°
∵AB∥CD,
∴EF∥CD,
…
请你补充完成嘉淇的解答过程:
问题迁移:请你参考嘉琪的解题思路,完成下面的问题:
如图3,AB∥CD,射线OM与直线AB,CD分别交于点A,C,射线ON与直线AB,CD分别交于点B,D,点P在射线ON上运动,设∠BAP=α,∠DCP=β.
(1)当点P在B,D两点之间运动时(P不与B,D重合),求α,β和∠APC之间满足的数量关系.
(2)当点P在B,D两点外侧运动时(P不与点O重合),直接写出α,β和∠APC之间满足的数量关系.
2018-2019学年河北省石家庄二十三中七年级(下)期末数学试卷
参考答案与试题解析
一、选择题(16个小题,1-10小题各3分,11-16小题各2分,共42分)
1.(3分)把58000表示成a×10n(其中1≤a≤10,n为整数)的形式,则n=( )
A.﹣4 B.2 C.3 D.4
【分析】用科学记数法表示较大的数时,一般形式为a×10n,其中1≤|a|<10,n为整数,据此判断即可.
【解答】解:把58000表示成a×10n(其中,1≤a<10,n为整数)的形式,故58000=5.8×104,
则n为4.
故选:D.
2.(3分)如图,∠3的同位角是( )
A.∠1 B.∠2 C.∠B D.∠C
【分析】根据两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线(截线)的同旁,则这样一对角叫做同位角.
【解答】解:观察图形可知:∠3的同位角是∠C.
故选:D.
3.(3分)下列等式从左到右的变形是因式分解的是( )
A.12a2b=3a?4ab B.ax﹣ay=a(x﹣y)
C.(x+2)(x﹣3)=x2﹣9 D.4x2+8x﹣1=4x(x+2)﹣1
【分析】把一个多项式化为几个整式的积的形式,这种变形叫做把这个多项式因式分解,也叫做分解因式.根据定义即可进行判断.
【解答】解:A.等式的左边不是多项式,原变形不是因式分解,故此选项不符合题意;
B.把一个多项式化为几个整式的积的形式,原变形是因式分解,故此选项符合题意;
C.原变形是整式的乘法,不是因式分解,故此选项不符合题意;
D.不是把一个多项式化为几个整式的积的形式,原变形不是因式分解,故此选项不符合题意;
故选:B.
4.(3分)如图,已知直线AB与CD平行,直线EF与AB,CD分别交于点E,F,若∠1=125°,则∠2=( )
A.65° B.55° C.50° D.45°
【分析】理由平行线的性质解决问题即可.
【解答】解:∵∠1=125°(已知),
∴∠AEC=180°﹣∠1=180°﹣125°=55°(邻补角互补),
∵AB∥CD(已知),
∴∠2=∠AEC=55°(两直线平行,内错角相等),
故选:B.
5.(3分)下列各式中,计算结果为a8的是( )
A.a4+a4 B.a16÷a2 C.a4?a4 D.(﹣2a4)2
【分析】直接利用同底数幂的乘除运算法则分别化简得出答案.
【解答】解:A、a4+a4=2a4,故此选项错误;
B、a16÷a2=a14,故此选项错误;
C、a4?a4=a8,正确;
D、(﹣2a4)2=4a8,故此选项错误;
故选:C.
6.(3分)若一个三角形两边长分别是5cm和8cm,则第三边长可能是( )
A.14cm B.13cm C.10cm D.﹣3cm
【分析】根据三角形的三边关系“任意两边之和大于第三边,任意两边之差小于第三边”,进行分析.
【解答】解:∵8﹣5<第三边<8+5,
∴3<第三边<13,
∴第三边的长度可能是10cm,
故选:C.
7.(3分)如图是测量嘉琪跳远成绩的示意图,直线l是起跳线,以下线段的长度能作为嘉琪跳远成绩的是( )
A.BP B.CP C.AP D.AO
【分析】利用垂线段最短求解.
【解答】解:该运动员跳远成绩的依据是:垂线段最短,符合题意的垂线段是AO;
故选:D.
8.(3分)解方程组,如果用加减消元法消去n,那么下列方法可行的是( )
A.①×4+②×3 B.①×4﹣②×3 C.①×3﹣②×4 D.①×3+②×4
【分析】利用加减消元法判断即可.
【解答】解:解方程组,如果用加减消元法消去n,那么下列方法可行的是①×3+②×4,
故选:D.
9.(3分)一副三角板如图放置,点D在CB的延长线上,EF∥CD,∠C=∠EDF=90°,∠A=45°,∠EFD=30°,则∠DFB=( )
A.15° B.20° C.25° D.30°
【分析】直接利用三角板的特点,结合平行线的性质得出∠BFE=45°,进而得出答案.
【解答】解:由题意可得:∠EFD=30°,∠ABC=45°,
∵EF∥CD,
∴∠BFE=∠ABC=45°,
∴∠DFB=45°﹣30°=15°.
故选:A.
10.(3分)下列命题:
①对顶角相等;②内错角相等;
③两条平行线之间的距离处处相等;
④有且只有一条直线垂直于已知直线.
其中是假命题的有( )
A.①② B.②④ C.②③ D.③④
【分析】利用对顶角的性质、平行线的性质等知识分别判断后即可确定正确的选项.
【解答】解:①对顶角相等,正确,是真命题;
②两直线平行,内错角相等,故错误,是假命题;
③两条平行线之间的距离处处相等,正确,是真命题;
④过一点有且只有一条直线垂直于已知直线,故错误,是假命题,
故选:B.
11.(2分)如图,已知有理数a,b,c在数轴上对应的点分别为A,B,C,则下列不等式中不正确的是( )
A.c<b<a B.ac>ab C.cb>ab D.c+b<a+b
【分析】先根据数轴的特点得出a>0>b>c,再根据不等式的性质进行判断.
【解答】解:由题意,可知a>0>b>c.
A、∵a>0>b>c,∴c<b<a,故此选项错误;
B、∵b>c,a>0,∴ac<ab,故此选项正确;
C、∵c<a,b<0,∴cb>ab,故此选项错误;
D、∵c<a,∴c+b<a+b,故此选项错误;
故选:B.
12.(2分)若x2﹣4x﹣1=0,则代数式2x(x﹣3)﹣(x﹣1)2+3的值为( )
A.3 B.4 C.1 D.0
【分析】利用单项式乘多项式的计算法则和完全平方公式先算乘方和乘法,然后再算加减,最后整体代入求值.
【解答】解:原式=2x2﹣6x﹣(x2﹣2x+1)+3
=2x2﹣6x﹣x2+2x﹣1+3
=x2﹣4x+2,
又∵x2﹣4x﹣1=0,
∴x2﹣4x=1,
∴原式=1+2=3,
故选:A.
13.(2分)若关于x的不等式组的解集为x>3,那么a的取值范围是( )
A.a>3 B.a<3 C.a≥3 D.a≤3
【分析】先求出每个不等式的解集,根据已知不等式组的解集即可得出答案.
【解答】解:
∵解不等式①得:x>3,
解不等式②得:x>a,
∵关于x的不等式组的解集为x>3,
∴a≤3,
故选:D.
14.(2分)如(x+m)与(x+3)的乘积中不含x的一次项,则m的值为( )
A.﹣3 B.3 C.0 D.1
【分析】先用多项式乘以多项式的运算法则展开求它们的积,并且把m看作常数合并关于x的同类项,令x的系数为0,得出关于m的方程,求出m的值.
【解答】解:∵(x+m)(x+3)=x2+3x+mx+3m=x2+(3+m)x+3m,
又∵(x+m)与(x+3)的乘积中不含x的一次项,
∴3+m=0,
解得m=﹣3.
故选:A.
15.(2分)在锐角三角形ABC中,∠A=50°,则∠B的范围是( )
A.0°<∠B<90° B.40°<∠B<130°
C.40°≤∠B≤90° D.40°<∠B<90°
【分析】根据三角形的内角和即可得到结论.
【解答】解:∵在锐角三角形ABC中,∠A=50°,则∠B的范围是40°<∠B<90°,
故选:D.
16.(2分)如图,在长方形ABCD中,AB=5,第一次平移将长方形ABCD沿AB方向向右平移4个单位长度,得到长方形A1B1C1D1,第二次平移将长方形A1B1C1D1沿A1B1方向向右平移4个单位长度,得到长方形A2B2C2D2,……,第n次平移将长方形An﹣1Bn﹣1Cn﹣1Dn﹣1沿An﹣1Bn﹣1方向向右平移4个单位长度,得到长方形AnBn?nDn(n>2).若ABn的长为45,则n=( )
A.10 B.11 C.16 D.9
【分析】根据题意先求出AB1=5+4,AB2=5+4+4,…从而发现ABn=5+4n,代入问题数值即可求解n.
【解答】解:由已知平移关系可知AB=5,AB1=5+4,AB2=5+4+4,…
所以ABn=5+4n.
当ABn的长为45时,5+4n=45,解得n=10.
故选:A.
二、填空题(共12分,每小题各3分)
17.(3分)已知关于x,y的二元一次方程mx﹣2y=2的一组解为,则m= 4 .
【分析】把代入方程mx﹣2y=2得出3m﹣10=2,求出m即可.
【解答】解:把代入方程mx﹣2y=2得:3m﹣10=2,
解得:m=4,
故答案为:4.
18.(3分)若有理数a,b满足|a+|+b2=0,则ab= 1 .
【分析】首先依据非负数的性质求得a、b的值,然后利用有理数的乘方求解即可.
【解答】解:∵|a+|+b2=0,
∴a=﹣,b=0.
∴ab=(﹣)0=1.
故答案为:1.
19.(3分)分解因式:x3y﹣2x2y+xy= xy(x﹣1)2 .
【分析】原式提取公因式,再利用完全平方公式分解即可.
【解答】解:原式=xy(x2﹣2x+1)=xy(x﹣1)2.
故答案为:xy(x﹣1)2
20.(3分)在如图所示的长方形中放置了8个形状、大小都相同的小长方形,则图中阴影部分的面积为 79 .
【分析】设小长方形的长为x,宽为y,根据长方形ABCD的长为17,宽的两种不同表达方式列出方程组求出小长方形的长和宽,进一步求出图中阴影部分的面积.
【解答】解:设小长方形的长为x,宽为y,根据题意得
,
解得,
∴S阴影=17×(9+3×2)﹣8×11×2=79.
故答案为:79.
三、解答题(共6个小题,共46分)
21.(12分)计算:
(1)解方程组:;
(2)解不等式组,并把解集在数轴上表示出来.
(3)已知:(x+1)(x+2)﹣ (x2﹣3x) =6x+2,请计算 (x2﹣3x) 内应填写的式子.
【分析】(1)利用加减法即可求得;
(2)首先解每个不等式,两个不等式的解集的公共部分就是不等式组的解集.
(3)利用减法法则可得减数所得的式子.
【解答】解:(1),
②﹣①得:4n=8,
n=2,
把n=2代入①得:2m﹣2=4,
m=3,
则方程组的解为:;
(2)
解①得x≤5,
解②得x≥2.
则不等式组的解集是2≤x≤5.
在数轴上表示不等式组的解集是:
(3)∵(x+1)(x+2)=x2+3x+2,
∴x2+3x+2﹣(6x+2)=x2+3x+2﹣6x﹣2=x2﹣3x,
故答案为:x2﹣3x.
22.(5分)在多项式的乘法公式中,完全平方公式是其中重要的一个.
(1)请你补全完全平方公式的推导过程:
(a+b)2=(a+b)(a+b)=a2+ ab + ab +b2=a2+ 2ab +b2
(2)如图,将边长为a+b的正方形分割成I,Ⅱ,Ⅲ,Ⅳ四部分,请用不同的方法分别表示出这个正方形的面积,并结合图形给出完全平方公式的几何解释.
【分析】(1)依据多项式乘多项式法则,即可得到结果;
(2)依据边长为a+b的正方形分割成Ⅰ、Ⅱ、Ⅲ、Ⅳ四部分,即可得到完全平方公式的几何解释;
【解答】解:(1)(a+b)2=(a+b)(a+b)
=a2+ab+ab+b2
=a2+2ab+b2
故答案为:ab,ab,2ab;
(2)边长为a+b的正方形的面积,等于边长分别为a和b的两个小正方形面积的和,再加上两个长为a,宽为b的长方形的面积.
23.(6分)请同学们观察以下三个算式,并结合这些算式,回答下列问题:
32﹣1=8×1
53﹣32=8×2
72﹣52=8×3
(1)请你再写出另外两个符合上述规律的算式: 92﹣72=8×4 ; 112﹣92=8×5 ;
(2)观察上述算式,我们发现:如果设两个连续的奇数分别为2n﹣1和2n+1(其中n为正整数),则它们的平方差是8的倍数;请用含n的式子说明上述规律的正确性.
【分析】(1)根据已知算式写出符合题意的答案;
(2)利用平方差公式计算得出答案;
【解答】解:(1)92﹣72=8×4,112﹣92=8×5;
故答案为:92﹣72=8×4;112﹣92=8×5;(答案不唯一)
(2)验证规律:设两个连续奇数为2n+1,2n﹣1(其中n为正整数),则它们的平方差是8的倍数;
(2n+1)2﹣(2n﹣1)2
=(2n+1﹣2n+1)(2n+1+2n﹣1)
=2×4n
=8n,
故两个连续奇数的平方差是8的倍数.
24.(7分)如图,AD,AE和AF分别是△ABC的高、角平分线和中线.
(1)对于下面的五个结论:
①BC=2BF;②∠CAE=∠CAB;③BE=CE;④AD⊥BC;⑤S△AFB=S△AFC.
其中错误的是 ③ (只填序号);
(2)若∠C=70°,∠ABC=28°,求∠DAE的度数.
【分析】(1)根据三角形的高、角平分线和中线的定义即可得到AD⊥BC,∠CAE=∠CAB,BC=2BF,S△AFB=S△AFC.
(2)先根据三角形内角和得到∠CAB=180°﹣∠ABC﹣∠C=82°,再根据角平分线与高线的定义得到∠CAE=∠CAB=41°,∠ADC=90°,则∠DAC=90°﹣∠C=20°,然后利用∠DAE=∠CAE﹣∠DAC计算即可.
【解答】解:(1)∵AD,AE和AF分别是△ABC的高、角平分线和中线,
∴AD⊥BC,∠CAE=∠BAE=∠CAB,BF=CF,BC=2BF,
∵S△AFB=BF?AD,S△AFC=CF?AD,
∴S△AFB=S△AFC,故①②④⑤正确,③错误,
故答案为③.
(2)∵∠C=70°,∠ABC=28°,
∴∠CAB=180°﹣∠ABC﹣∠C=82°,
∴∠CAE=∠CAB=41°,
∵∠ADC=90°,∠C=70°,
∴∠DAC=20°
∴∠DAE=∠CAE﹣∠DAC=41°﹣20°=21°.
25.(7分)某超市分别以每盏150元,190元的进价购进A,B两种品牌的护眼灯,下表是近两天的销售情况.
销售日期 销售数量(盏) 销售收入(元)
A品牌 B品牌
第一天 2 1 680
第二天 3 4 1670
(1)求A,B两种品牌护眼灯的销售价;
(2)若超市准备用不超过4900元的金额购进这两种品牌的护眼灯共30盏,求B品牌的护眼灯最多采购多少盏?
【分析】(1)设A品牌护眼灯的销售价为x元/盏,B品牌护眼灯的销售价为y元/盏,根据总价=单价×数量结合两天的销售情况,即可得出关于x,y的二元一次方程组,解之即可得出结论;
(2)设采购m盏B品牌的护眼灯,则采购(30﹣m)盏A品牌的护眼灯,根据总价=单价×数量结合总费用不超过4900元,即可得出关于m的一元一次不等式,解之取其中的最大值即可得出结论.
【解答】解:(1)设A品牌护眼灯的销售价为x元/盏,B品牌护眼灯的销售价为y元/盏,
依题意,得:,
解得:.
答:A品牌护眼灯的销售价为210元/盏,B品牌护眼灯的销售价为260元/盏.
(2)设采购m盏B品牌的护眼灯,则采购(30﹣m)盏A品牌的护眼灯,
依题意,得:150(30﹣m)+190m≤4900,
解得:m≤10.
答:B品牌的护眼灯最多采购10盏.
26.(9分)问题解决:如图1,已知AB∥CD,E是直线AB,CD内部一点,连接BE,DE,若∠ABE=40°,∠CDE=60°,求∠BED的度数.
嘉琪想到了如图2所示的方法,但是没有解答完,下面是嘉淇未完成的解答过程:
解:过点E作EF∥AB,
∴∠ABE=∠BEF=40°
∵AB∥CD,
∴EF∥CD,
…
请你补充完成嘉淇的解答过程:
问题迁移:请你参考嘉琪的解题思路,完成下面的问题:
如图3,AB∥CD,射线OM与直线AB,CD分别交于点A,C,射线ON与直线AB,CD分别交于点B,D,点P在射线ON上运动,设∠BAP=α,∠DCP=β.
(1)当点P在B,D两点之间运动时(P不与B,D重合),求α,β和∠APC之间满足的数量关系.
(2)当点P在B,D两点外侧运动时(P不与点O重合),直接写出α,β和∠APC之间满足的数量关系.
【分析】问题解决:过点E作EF∥AB,依据平行线的性质,即可得到∠BED的度数;
问题迁移:(1)过P作PQ∥AB,依据平行线的性质,即可得出α,β和∠APC之间满足的数量关系.
(2)分两种情况讨论:过P作PQ∥AB,易得当点P在BN上时,∠APC=β﹣α;当点P在OD上时,∠APC=α﹣β.
【解答】解:问题解决:
如图2,过点E作EF∥AB,
∴∠ABE=∠BEF=40°
∵AB∥CD,
∴EF∥CD,
∴∠B=∠BEF,∠D=∠DEF,
∴∠BED=∠B+∠D=40°+60°=100°;
问题迁移:
(1)如图3,过P作PQ∥AB,
∵AB∥CD,
∴PQ∥CD,
∴∠BAP=∠APQ,∠DCP=∠CPQ,
∴∠APC=∠BAP+∠DCP,即∠APC=α+β;
(2)如图4,当点P在BN上时,∠APC=β﹣α;
如图5,当点P在OD上时,∠APC=α﹣β.
一、选择题(16个小题,1-10小题各3分,11-16小题各2分,共42分)
1.(3分)把58000表示成a×10n(其中1≤a≤10,n为整数)的形式,则n=( )
A.﹣4 B.2 C.3 D.4
2.(3分)如图,∠3的同位角是( )
A.∠1 B.∠2 C.∠B D.∠C
3.(3分)下列等式从左到右的变形是因式分解的是( )
A.12a2b=3a?4ab B.ax﹣ay=a(x﹣y)
C.(x+2)(x﹣3)=x2﹣9 D.4x2+8x﹣1=4x(x+2)﹣1
4.(3分)如图,已知直线AB与CD平行,直线EF与AB,CD分别交于点E,F,若∠1=125°,则∠2=( )
A.65° B.55° C.50° D.45°
5.(3分)下列各式中,计算结果为a8的是( )
A.a4+a4 B.a16÷a2 C.a4?a4 D.(﹣2a4)2
6.(3分)若一个三角形两边长分别是5cm和8cm,则第三边长可能是( )
A.14cm B.13cm C.10cm D.﹣3cm
7.(3分)如图是测量嘉琪跳远成绩的示意图,直线l是起跳线,以下线段的长度能作为嘉琪跳远成绩的是( )
A.BP B.CP C.AP D.AO
8.(3分)解方程组,如果用加减消元法消去n,那么下列方法可行的是( )
A.①×4+②×3 B.①×4﹣②×3 C.①×3﹣②×4 D.①×3+②×4
9.(3分)一副三角板如图放置,点D在CB的延长线上,EF∥CD,∠C=∠EDF=90°,∠A=45°,∠EFD=30°,则∠DFB=( )
A.15° B.20° C.25° D.30°
10.(3分)下列命题:
①对顶角相等;②内错角相等;
③两条平行线之间的距离处处相等;
④有且只有一条直线垂直于已知直线.
其中是假命题的有( )
A.①② B.②④ C.②③ D.③④
11.(2分)如图,已知有理数a,b,c在数轴上对应的点分别为A,B,C,则下列不等式中不正确的是( )
A.c<b<a B.ac>ab C.cb>ab D.c+b<a+b
12.(2分)若x2﹣4x﹣1=0,则代数式2x(x﹣3)﹣(x﹣1)2+3的值为( )
A.3 B.4 C.1 D.0
13.(2分)若关于x的不等式组的解集为x>3,那么a的取值范围是( )
A.a>3 B.a<3 C.a≥3 D.a≤3
14.(2分)如(x+m)与(x+3)的乘积中不含x的一次项,则m的值为( )
A.﹣3 B.3 C.0 D.1
15.(2分)在锐角三角形ABC中,∠A=50°,则∠B的范围是( )
A.0°<∠B<90° B.40°<∠B<130°
C.40°≤∠B≤90° D.40°<∠B<90°
16.(2分)如图,在长方形ABCD中,AB=5,第一次平移将长方形ABCD沿AB方向向右平移4个单位长度,得到长方形A1B1C1D1,第二次平移将长方形A1B1C1D1沿A1B1方向向右平移4个单位长度,得到长方形A2B2C2D2,……,第n次平移将长方形An﹣1Bn﹣1Cn﹣1Dn﹣1沿An﹣1Bn﹣1方向向右平移4个单位长度,得到长方形AnBn?nDn(n>2).若ABn的长为45,则n=( )
A.10 B.11 C.16 D.9
二、填空题(共12分,每小题各3分)
17.(3分)已知关于x,y的二元一次方程mx﹣2y=2的一组解为,则m= .
18.(3分)若有理数a,b满足|a+|+b2=0,则ab= .
19.(3分)分解因式:x3y﹣2x2y+xy= .
20.(3分)在如图所示的长方形中放置了8个形状、大小都相同的小长方形,则图中阴影部分的面积为 .
三、解答题(共6个小题,共46分)
21.(12分)计算:
(1)解方程组:;
(2)解不等式组,并把解集在数轴上表示出来.
(3)已知:(x+1)(x+2)﹣ =6x+2,请计算 内应填写的式子.
22.(5分)在多项式的乘法公式中,完全平方公式是其中重要的一个.
(1)请你补全完全平方公式的推导过程:
(a+b)2=(a+b)(a+b)=a2+ + +b2=a2+ +b2
(2)如图,将边长为a+b的正方形分割成I,Ⅱ,Ⅲ,Ⅳ四部分,请用不同的方法分别表示出这个正方形的面积,并结合图形给出完全平方公式的几何解释.
23.(6分)请同学们观察以下三个算式,并结合这些算式,回答下列问题:
32﹣1=8×1
53﹣32=8×2
72﹣52=8×3
(1)请你再写出另外两个符合上述规律的算式: ; ;
(2)观察上述算式,我们发现:如果设两个连续的奇数分别为2n﹣1和2n+1(其中n为正整数),则它们的平方差是8的倍数;请用含n的式子说明上述规律的正确性.
24.(7分)如图,AD,AE和AF分别是△ABC的高、角平分线和中线.
(1)对于下面的五个结论:
①BC=2BF;②∠CAE=∠CAB;③BE=CE;④AD⊥BC;⑤S△AFB=S△AFC.
其中错误的是 (只填序号);
(2)若∠C=70°,∠ABC=28°,求∠DAE的度数.
25.(7分)某超市分别以每盏150元,190元的进价购进A,B两种品牌的护眼灯,下表是近两天的销售情况.
销售日期 销售数量(盏) 销售收入(元)
A品牌 B品牌
第一天 2 1 680
第二天 3 4 1670
(1)求A,B两种品牌护眼灯的销售价;
(2)若超市准备用不超过4900元的金额购进这两种品牌的护眼灯共30盏,求B品牌的护眼灯最多采购多少盏?
26.(9分)问题解决:如图1,已知AB∥CD,E是直线AB,CD内部一点,连接BE,DE,若∠ABE=40°,∠CDE=60°,求∠BED的度数.
嘉琪想到了如图2所示的方法,但是没有解答完,下面是嘉淇未完成的解答过程:
解:过点E作EF∥AB,
∴∠ABE=∠BEF=40°
∵AB∥CD,
∴EF∥CD,
…
请你补充完成嘉淇的解答过程:
问题迁移:请你参考嘉琪的解题思路,完成下面的问题:
如图3,AB∥CD,射线OM与直线AB,CD分别交于点A,C,射线ON与直线AB,CD分别交于点B,D,点P在射线ON上运动,设∠BAP=α,∠DCP=β.
(1)当点P在B,D两点之间运动时(P不与B,D重合),求α,β和∠APC之间满足的数量关系.
(2)当点P在B,D两点外侧运动时(P不与点O重合),直接写出α,β和∠APC之间满足的数量关系.
2018-2019学年河北省石家庄二十三中七年级(下)期末数学试卷
参考答案与试题解析
一、选择题(16个小题,1-10小题各3分,11-16小题各2分,共42分)
1.(3分)把58000表示成a×10n(其中1≤a≤10,n为整数)的形式,则n=( )
A.﹣4 B.2 C.3 D.4
【分析】用科学记数法表示较大的数时,一般形式为a×10n,其中1≤|a|<10,n为整数,据此判断即可.
【解答】解:把58000表示成a×10n(其中,1≤a<10,n为整数)的形式,故58000=5.8×104,
则n为4.
故选:D.
2.(3分)如图,∠3的同位角是( )
A.∠1 B.∠2 C.∠B D.∠C
【分析】根据两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线(截线)的同旁,则这样一对角叫做同位角.
【解答】解:观察图形可知:∠3的同位角是∠C.
故选:D.
3.(3分)下列等式从左到右的变形是因式分解的是( )
A.12a2b=3a?4ab B.ax﹣ay=a(x﹣y)
C.(x+2)(x﹣3)=x2﹣9 D.4x2+8x﹣1=4x(x+2)﹣1
【分析】把一个多项式化为几个整式的积的形式,这种变形叫做把这个多项式因式分解,也叫做分解因式.根据定义即可进行判断.
【解答】解:A.等式的左边不是多项式,原变形不是因式分解,故此选项不符合题意;
B.把一个多项式化为几个整式的积的形式,原变形是因式分解,故此选项符合题意;
C.原变形是整式的乘法,不是因式分解,故此选项不符合题意;
D.不是把一个多项式化为几个整式的积的形式,原变形不是因式分解,故此选项不符合题意;
故选:B.
4.(3分)如图,已知直线AB与CD平行,直线EF与AB,CD分别交于点E,F,若∠1=125°,则∠2=( )
A.65° B.55° C.50° D.45°
【分析】理由平行线的性质解决问题即可.
【解答】解:∵∠1=125°(已知),
∴∠AEC=180°﹣∠1=180°﹣125°=55°(邻补角互补),
∵AB∥CD(已知),
∴∠2=∠AEC=55°(两直线平行,内错角相等),
故选:B.
5.(3分)下列各式中,计算结果为a8的是( )
A.a4+a4 B.a16÷a2 C.a4?a4 D.(﹣2a4)2
【分析】直接利用同底数幂的乘除运算法则分别化简得出答案.
【解答】解:A、a4+a4=2a4,故此选项错误;
B、a16÷a2=a14,故此选项错误;
C、a4?a4=a8,正确;
D、(﹣2a4)2=4a8,故此选项错误;
故选:C.
6.(3分)若一个三角形两边长分别是5cm和8cm,则第三边长可能是( )
A.14cm B.13cm C.10cm D.﹣3cm
【分析】根据三角形的三边关系“任意两边之和大于第三边,任意两边之差小于第三边”,进行分析.
【解答】解:∵8﹣5<第三边<8+5,
∴3<第三边<13,
∴第三边的长度可能是10cm,
故选:C.
7.(3分)如图是测量嘉琪跳远成绩的示意图,直线l是起跳线,以下线段的长度能作为嘉琪跳远成绩的是( )
A.BP B.CP C.AP D.AO
【分析】利用垂线段最短求解.
【解答】解:该运动员跳远成绩的依据是:垂线段最短,符合题意的垂线段是AO;
故选:D.
8.(3分)解方程组,如果用加减消元法消去n,那么下列方法可行的是( )
A.①×4+②×3 B.①×4﹣②×3 C.①×3﹣②×4 D.①×3+②×4
【分析】利用加减消元法判断即可.
【解答】解:解方程组,如果用加减消元法消去n,那么下列方法可行的是①×3+②×4,
故选:D.
9.(3分)一副三角板如图放置,点D在CB的延长线上,EF∥CD,∠C=∠EDF=90°,∠A=45°,∠EFD=30°,则∠DFB=( )
A.15° B.20° C.25° D.30°
【分析】直接利用三角板的特点,结合平行线的性质得出∠BFE=45°,进而得出答案.
【解答】解:由题意可得:∠EFD=30°,∠ABC=45°,
∵EF∥CD,
∴∠BFE=∠ABC=45°,
∴∠DFB=45°﹣30°=15°.
故选:A.
10.(3分)下列命题:
①对顶角相等;②内错角相等;
③两条平行线之间的距离处处相等;
④有且只有一条直线垂直于已知直线.
其中是假命题的有( )
A.①② B.②④ C.②③ D.③④
【分析】利用对顶角的性质、平行线的性质等知识分别判断后即可确定正确的选项.
【解答】解:①对顶角相等,正确,是真命题;
②两直线平行,内错角相等,故错误,是假命题;
③两条平行线之间的距离处处相等,正确,是真命题;
④过一点有且只有一条直线垂直于已知直线,故错误,是假命题,
故选:B.
11.(2分)如图,已知有理数a,b,c在数轴上对应的点分别为A,B,C,则下列不等式中不正确的是( )
A.c<b<a B.ac>ab C.cb>ab D.c+b<a+b
【分析】先根据数轴的特点得出a>0>b>c,再根据不等式的性质进行判断.
【解答】解:由题意,可知a>0>b>c.
A、∵a>0>b>c,∴c<b<a,故此选项错误;
B、∵b>c,a>0,∴ac<ab,故此选项正确;
C、∵c<a,b<0,∴cb>ab,故此选项错误;
D、∵c<a,∴c+b<a+b,故此选项错误;
故选:B.
12.(2分)若x2﹣4x﹣1=0,则代数式2x(x﹣3)﹣(x﹣1)2+3的值为( )
A.3 B.4 C.1 D.0
【分析】利用单项式乘多项式的计算法则和完全平方公式先算乘方和乘法,然后再算加减,最后整体代入求值.
【解答】解:原式=2x2﹣6x﹣(x2﹣2x+1)+3
=2x2﹣6x﹣x2+2x﹣1+3
=x2﹣4x+2,
又∵x2﹣4x﹣1=0,
∴x2﹣4x=1,
∴原式=1+2=3,
故选:A.
13.(2分)若关于x的不等式组的解集为x>3,那么a的取值范围是( )
A.a>3 B.a<3 C.a≥3 D.a≤3
【分析】先求出每个不等式的解集,根据已知不等式组的解集即可得出答案.
【解答】解:
∵解不等式①得:x>3,
解不等式②得:x>a,
∵关于x的不等式组的解集为x>3,
∴a≤3,
故选:D.
14.(2分)如(x+m)与(x+3)的乘积中不含x的一次项,则m的值为( )
A.﹣3 B.3 C.0 D.1
【分析】先用多项式乘以多项式的运算法则展开求它们的积,并且把m看作常数合并关于x的同类项,令x的系数为0,得出关于m的方程,求出m的值.
【解答】解:∵(x+m)(x+3)=x2+3x+mx+3m=x2+(3+m)x+3m,
又∵(x+m)与(x+3)的乘积中不含x的一次项,
∴3+m=0,
解得m=﹣3.
故选:A.
15.(2分)在锐角三角形ABC中,∠A=50°,则∠B的范围是( )
A.0°<∠B<90° B.40°<∠B<130°
C.40°≤∠B≤90° D.40°<∠B<90°
【分析】根据三角形的内角和即可得到结论.
【解答】解:∵在锐角三角形ABC中,∠A=50°,则∠B的范围是40°<∠B<90°,
故选:D.
16.(2分)如图,在长方形ABCD中,AB=5,第一次平移将长方形ABCD沿AB方向向右平移4个单位长度,得到长方形A1B1C1D1,第二次平移将长方形A1B1C1D1沿A1B1方向向右平移4个单位长度,得到长方形A2B2C2D2,……,第n次平移将长方形An﹣1Bn﹣1Cn﹣1Dn﹣1沿An﹣1Bn﹣1方向向右平移4个单位长度,得到长方形AnBn?nDn(n>2).若ABn的长为45,则n=( )
A.10 B.11 C.16 D.9
【分析】根据题意先求出AB1=5+4,AB2=5+4+4,…从而发现ABn=5+4n,代入问题数值即可求解n.
【解答】解:由已知平移关系可知AB=5,AB1=5+4,AB2=5+4+4,…
所以ABn=5+4n.
当ABn的长为45时,5+4n=45,解得n=10.
故选:A.
二、填空题(共12分,每小题各3分)
17.(3分)已知关于x,y的二元一次方程mx﹣2y=2的一组解为,则m= 4 .
【分析】把代入方程mx﹣2y=2得出3m﹣10=2,求出m即可.
【解答】解:把代入方程mx﹣2y=2得:3m﹣10=2,
解得:m=4,
故答案为:4.
18.(3分)若有理数a,b满足|a+|+b2=0,则ab= 1 .
【分析】首先依据非负数的性质求得a、b的值,然后利用有理数的乘方求解即可.
【解答】解:∵|a+|+b2=0,
∴a=﹣,b=0.
∴ab=(﹣)0=1.
故答案为:1.
19.(3分)分解因式:x3y﹣2x2y+xy= xy(x﹣1)2 .
【分析】原式提取公因式,再利用完全平方公式分解即可.
【解答】解:原式=xy(x2﹣2x+1)=xy(x﹣1)2.
故答案为:xy(x﹣1)2
20.(3分)在如图所示的长方形中放置了8个形状、大小都相同的小长方形,则图中阴影部分的面积为 79 .
【分析】设小长方形的长为x,宽为y,根据长方形ABCD的长为17,宽的两种不同表达方式列出方程组求出小长方形的长和宽,进一步求出图中阴影部分的面积.
【解答】解:设小长方形的长为x,宽为y,根据题意得
,
解得,
∴S阴影=17×(9+3×2)﹣8×11×2=79.
故答案为:79.
三、解答题(共6个小题,共46分)
21.(12分)计算:
(1)解方程组:;
(2)解不等式组,并把解集在数轴上表示出来.
(3)已知:(x+1)(x+2)﹣ (x2﹣3x) =6x+2,请计算 (x2﹣3x) 内应填写的式子.
【分析】(1)利用加减法即可求得;
(2)首先解每个不等式,两个不等式的解集的公共部分就是不等式组的解集.
(3)利用减法法则可得减数所得的式子.
【解答】解:(1),
②﹣①得:4n=8,
n=2,
把n=2代入①得:2m﹣2=4,
m=3,
则方程组的解为:;
(2)
解①得x≤5,
解②得x≥2.
则不等式组的解集是2≤x≤5.
在数轴上表示不等式组的解集是:
(3)∵(x+1)(x+2)=x2+3x+2,
∴x2+3x+2﹣(6x+2)=x2+3x+2﹣6x﹣2=x2﹣3x,
故答案为:x2﹣3x.
22.(5分)在多项式的乘法公式中,完全平方公式是其中重要的一个.
(1)请你补全完全平方公式的推导过程:
(a+b)2=(a+b)(a+b)=a2+ ab + ab +b2=a2+ 2ab +b2
(2)如图,将边长为a+b的正方形分割成I,Ⅱ,Ⅲ,Ⅳ四部分,请用不同的方法分别表示出这个正方形的面积,并结合图形给出完全平方公式的几何解释.
【分析】(1)依据多项式乘多项式法则,即可得到结果;
(2)依据边长为a+b的正方形分割成Ⅰ、Ⅱ、Ⅲ、Ⅳ四部分,即可得到完全平方公式的几何解释;
【解答】解:(1)(a+b)2=(a+b)(a+b)
=a2+ab+ab+b2
=a2+2ab+b2
故答案为:ab,ab,2ab;
(2)边长为a+b的正方形的面积,等于边长分别为a和b的两个小正方形面积的和,再加上两个长为a,宽为b的长方形的面积.
23.(6分)请同学们观察以下三个算式,并结合这些算式,回答下列问题:
32﹣1=8×1
53﹣32=8×2
72﹣52=8×3
(1)请你再写出另外两个符合上述规律的算式: 92﹣72=8×4 ; 112﹣92=8×5 ;
(2)观察上述算式,我们发现:如果设两个连续的奇数分别为2n﹣1和2n+1(其中n为正整数),则它们的平方差是8的倍数;请用含n的式子说明上述规律的正确性.
【分析】(1)根据已知算式写出符合题意的答案;
(2)利用平方差公式计算得出答案;
【解答】解:(1)92﹣72=8×4,112﹣92=8×5;
故答案为:92﹣72=8×4;112﹣92=8×5;(答案不唯一)
(2)验证规律:设两个连续奇数为2n+1,2n﹣1(其中n为正整数),则它们的平方差是8的倍数;
(2n+1)2﹣(2n﹣1)2
=(2n+1﹣2n+1)(2n+1+2n﹣1)
=2×4n
=8n,
故两个连续奇数的平方差是8的倍数.
24.(7分)如图,AD,AE和AF分别是△ABC的高、角平分线和中线.
(1)对于下面的五个结论:
①BC=2BF;②∠CAE=∠CAB;③BE=CE;④AD⊥BC;⑤S△AFB=S△AFC.
其中错误的是 ③ (只填序号);
(2)若∠C=70°,∠ABC=28°,求∠DAE的度数.
【分析】(1)根据三角形的高、角平分线和中线的定义即可得到AD⊥BC,∠CAE=∠CAB,BC=2BF,S△AFB=S△AFC.
(2)先根据三角形内角和得到∠CAB=180°﹣∠ABC﹣∠C=82°,再根据角平分线与高线的定义得到∠CAE=∠CAB=41°,∠ADC=90°,则∠DAC=90°﹣∠C=20°,然后利用∠DAE=∠CAE﹣∠DAC计算即可.
【解答】解:(1)∵AD,AE和AF分别是△ABC的高、角平分线和中线,
∴AD⊥BC,∠CAE=∠BAE=∠CAB,BF=CF,BC=2BF,
∵S△AFB=BF?AD,S△AFC=CF?AD,
∴S△AFB=S△AFC,故①②④⑤正确,③错误,
故答案为③.
(2)∵∠C=70°,∠ABC=28°,
∴∠CAB=180°﹣∠ABC﹣∠C=82°,
∴∠CAE=∠CAB=41°,
∵∠ADC=90°,∠C=70°,
∴∠DAC=20°
∴∠DAE=∠CAE﹣∠DAC=41°﹣20°=21°.
25.(7分)某超市分别以每盏150元,190元的进价购进A,B两种品牌的护眼灯,下表是近两天的销售情况.
销售日期 销售数量(盏) 销售收入(元)
A品牌 B品牌
第一天 2 1 680
第二天 3 4 1670
(1)求A,B两种品牌护眼灯的销售价;
(2)若超市准备用不超过4900元的金额购进这两种品牌的护眼灯共30盏,求B品牌的护眼灯最多采购多少盏?
【分析】(1)设A品牌护眼灯的销售价为x元/盏,B品牌护眼灯的销售价为y元/盏,根据总价=单价×数量结合两天的销售情况,即可得出关于x,y的二元一次方程组,解之即可得出结论;
(2)设采购m盏B品牌的护眼灯,则采购(30﹣m)盏A品牌的护眼灯,根据总价=单价×数量结合总费用不超过4900元,即可得出关于m的一元一次不等式,解之取其中的最大值即可得出结论.
【解答】解:(1)设A品牌护眼灯的销售价为x元/盏,B品牌护眼灯的销售价为y元/盏,
依题意,得:,
解得:.
答:A品牌护眼灯的销售价为210元/盏,B品牌护眼灯的销售价为260元/盏.
(2)设采购m盏B品牌的护眼灯,则采购(30﹣m)盏A品牌的护眼灯,
依题意,得:150(30﹣m)+190m≤4900,
解得:m≤10.
答:B品牌的护眼灯最多采购10盏.
26.(9分)问题解决:如图1,已知AB∥CD,E是直线AB,CD内部一点,连接BE,DE,若∠ABE=40°,∠CDE=60°,求∠BED的度数.
嘉琪想到了如图2所示的方法,但是没有解答完,下面是嘉淇未完成的解答过程:
解:过点E作EF∥AB,
∴∠ABE=∠BEF=40°
∵AB∥CD,
∴EF∥CD,
…
请你补充完成嘉淇的解答过程:
问题迁移:请你参考嘉琪的解题思路,完成下面的问题:
如图3,AB∥CD,射线OM与直线AB,CD分别交于点A,C,射线ON与直线AB,CD分别交于点B,D,点P在射线ON上运动,设∠BAP=α,∠DCP=β.
(1)当点P在B,D两点之间运动时(P不与B,D重合),求α,β和∠APC之间满足的数量关系.
(2)当点P在B,D两点外侧运动时(P不与点O重合),直接写出α,β和∠APC之间满足的数量关系.
【分析】问题解决:过点E作EF∥AB,依据平行线的性质,即可得到∠BED的度数;
问题迁移:(1)过P作PQ∥AB,依据平行线的性质,即可得出α,β和∠APC之间满足的数量关系.
(2)分两种情况讨论:过P作PQ∥AB,易得当点P在BN上时,∠APC=β﹣α;当点P在OD上时,∠APC=α﹣β.
【解答】解:问题解决:
如图2,过点E作EF∥AB,
∴∠ABE=∠BEF=40°
∵AB∥CD,
∴EF∥CD,
∴∠B=∠BEF,∠D=∠DEF,
∴∠BED=∠B+∠D=40°+60°=100°;
问题迁移:
(1)如图3,过P作PQ∥AB,
∵AB∥CD,
∴PQ∥CD,
∴∠BAP=∠APQ,∠DCP=∠CPQ,
∴∠APC=∠BAP+∠DCP,即∠APC=α+β;
(2)如图4,当点P在BN上时,∠APC=β﹣α;
如图5,当点P在OD上时,∠APC=α﹣β.
同课章节目录
