2020-2021学年黑龙江省哈尔滨市通河县八年级(下)期末数学试卷(Word版 含解析)
文档属性
| 名称 | 2020-2021学年黑龙江省哈尔滨市通河县八年级(下)期末数学试卷(Word版 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 555.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-17 07:08:59 | ||
图片预览




文档简介
2020-2021学年黑龙江省哈尔滨市通河县八年级(下)期末数学试卷
一、填空题(每小题3分,共计30分)
1.(3分)下列运算正确的是( )
A.+= B.=7 C.÷=3 D.=﹣6
2.(3分)下列二次根式中,是最简二次根式的是( )
A. B. C. D.
3.(3分)在直角坐标系中,点P(﹣2,3)到原点的距离是( )
A. B. C. D.2
4.(3分)下列图形中,是轴对称图形的有( )
A.4个 B.3个 C.2个 D.1个
5.(3分)下列各组数中,能作为直角三角形的三边长的是( )
A.4,5,6 B.6,8,11 C.5,22,24 D.7,24,25
6.(3分)在平行四边形ABCD中,若∠A=115°,则∠D的度数是( )
A.105° B.115° C.125° D.65°
7.(3分)若正比例函数y=kx(k≠0)的图象过点(1,﹣2),则k的值是( )
A. B.2 C.﹣ D.﹣2
8.(3分)直线y=2x﹣4与两坐标轴所围成的三角形面积等于( )
A.2 B.4 C.6 D.8
9.(3分)如图,菱形ABCD中,对角线AC、BD相交于点O,H为AD边的中点,菱形的周长为28,则OH的长为( )
A.3.5 B.4.5 C.7 D.14
10.(3分)端午节期间,甲、乙两队举行了一年一度的赛龙舟比赛,两队在比赛时的路程s(米)与时间t(分钟)之间的函数关系如图所示,请你根据图象判断,下列说法正确的是( )
A.甲队率先到达终点
B.甲队比乙队多走了200米
C.乙队的速度始终比甲队的速度大
D.乙队比甲队少用0.2分钟
二、填空题(每小题3分,共计30分)
11.(3分)函数y=的自变量x的取值范围是 .
12.(3分)计算:5÷×= .
13.(3分)如图,把矩形ABCD沿EF折叠,若∠1=40°,则∠AEF= °.
14.(3分)一次函数y=﹣2x+5的图象不经过第 象限.
15.(3分)已知a、b为两个连续的整数,且,则a+b= .
16.(3分)若一次函数y=(m﹣4)x+3中,y随x的增大而增大,则m的取值范围是 .
17.(3分)如图,?ABCD中,AB=3,AD=5,对角线AC的垂直平分线交AD边于点E,则△CDE的周长为 .
18.(3分)已知△ABC中,∠A=30°,AB=4,BC=,则AC= .
19.(3分)如图,在?ABCD中,按以下步骤作图:①以C为圆心,以适当长为半径画弧,分别交BC,CD于M,N两点;②分别以M,N为圆心,以大于MN的长为半径画弧,两弧在∠BCD的内部交于点P;⑨连接CP并延长交AD于E.若AE=2,CE=6,∠B=60°,则ABCD的周长等于 .
20.(3分)已知矩形ABCD,点E在AD边上,DE>AE,连接BE,将△ABE沿着BE翻折得到△BFE,射线EF交BC于G,若点G为BC的中点,FG=1,DE=6,则BE长为 .
三、解答题(本题60分,其中21题8分,22每题7分,23题7分,24题8分,25、26、27每题各10分)
21.(8分)计算:
(1)(﹣)﹣(+);
(2)(2+)(2﹣)÷.
22.(7分)如图所示,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫格点,以格点为顶点分别按下列要求画图,要求它的顶点均在格点上.
(1)在图①中画一个面积为10的正方形.
(2)在图②中画一个面积为12的菱形,并直接写出这个菱形的周长.
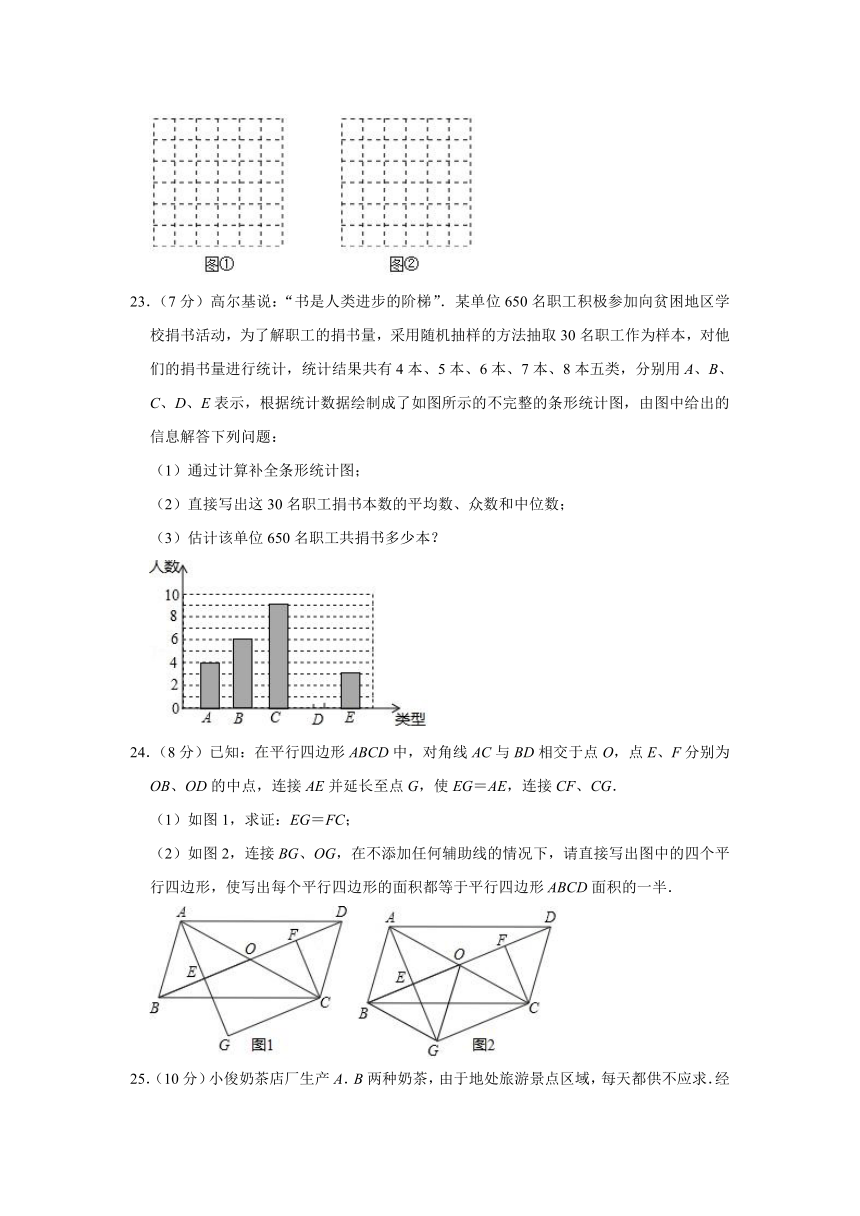
23.(7分)高尔基说:“书是人类进步的阶梯”.某单位650名职工积极参加向贫困地区学校捐书活动,为了解职工的捐书量,采用随机抽样的方法抽取30名职工作为样本,对他们的捐书量进行统计,统计结果共有4本、5本、6本、7本、8本五类,分别用A、B、C、D、E表示,根据统计数据绘制成了如图所示的不完整的条形统计图,由图中给出的信息解答下列问题:
(1)通过计算补全条形统计图;
(2)直接写出这30名职工捐书本数的平均数、众数和中位数;
(3)估计该单位650名职工共捐书多少本?
24.(8分)已知:在平行四边形ABCD中,对角线AC与BD相交于点O,点E、F分别为OB、OD的中点,连接AE并延长至点G,使EG=AE,连接CF、CG.
(1)如图1,求证:EG=FC;
(2)如图2,连接BG、OG,在不添加任何辅助线的情况下,请直接写出图中的四个平行四边形,使写出每个平行四边形的面积都等于平行四边形ABCD面积的一半.
25.(10分)小俊奶茶店厂生产A.B两种奶茶,由于地处旅游景点区域,每天都供不应求.经过数学计算,小俊发现A种奶茶每杯生产时间为4分钟,B种奶茶每杯生产时间为1分钟,由于原料和运营时间限制,每天生产的总时间为300分钟.
(1)设A种奶茶生产x杯,B种奶茶生产y杯,则y与x之间的函数关系式y= .
(2)由于A种奶茶比较受顾客青睐,小俊决定每天生产A种奶茶不少于73杯,那么不同的生产方案有多少种?并写出每种生产方案.
(3)在(2)情况下,若A种奶茶每杯利润为3元,B种奶茶每杯利润为1元,直接写出小俊每天获得的最大利润为 .
26.(10分)如图,四边形ABCD是正方形,点G是BC边上任意一点,DE⊥AG于点E,BF∥DE且交AG于点F.
(1)求证:AE=BF;
(2)如图2,连接DF、CE,探究线段DF与CE的关系并证明;
(3)图1中,若AB=8,BG=6,求EF长.
27.(10分)如图1,平面直角坐标系中,直线y=﹣x+b交x轴于点A(8,0),交y轴正半轴于点B.
(1)求点B的坐标;
(2)如图2,直线BC交x轴负半轴于点C,且AB=AC,P为线段BC上一点,过点P作x轴的平行线交直线AB于点Q,设点P的横坐标为m,线段PQ的长为d,求d与m之间的函数关系式;
(3)在(2)的条件下,M为CB延长线上一点,且BM=CP,在线段AB上是否存在点N,使△PMN是以PM为斜边的等腰直角三角形,若存在,请求出点N的坐标;若不存在,请说明理由.
2020-2021学年黑龙江省哈尔滨市通河县八年级(下)期末数学试卷
参考答案与试题解析
一、填空题(每小题3分,共计30分)
1.(3分)下列运算正确的是( )
A.+= B.=7 C.÷=3 D.=﹣6
【分析】根据各个选项中的式子,可以计算出正确的结果,从而可以解答本题.
【解答】解:+不能合并,故选项A不符合题意;
===5,故选项B不符合题意;
==3,故选项C符合题意;
=6,故选项D不符合题意;
故选:C.
2.(3分)下列二次根式中,是最简二次根式的是( )
A. B. C. D.
【分析】A:应用算术平方根的算法进行求解即可得出答案;
B:应用最简二次根式的定义进行求解即可得出答案;
C:应用二次根式的乘法法则进行求解即可得出答案;
D:应用二次根式除法法则进行求解即可得出答案.
【解答】解:A:∵=3,∴A选项不符合题意;
B:∵是最简二次根式,∴B选项符合题意;
C:∵=3|a|,∴C选项不符合题意;
D:∵==,∴D选项不符合题意.
故选:B.
3.(3分)在直角坐标系中,点P(﹣2,3)到原点的距离是( )
A. B. C. D.2
【分析】在平面直角坐标系中找出P点,过P作PE垂直于x轴,连接OP,由P的坐标得出PE及OE的长,在直角三角形OPE中,由PE及OE的长,利用勾股定理求出OP的长,即为P到原点的距离.
【解答】解:过P作PE⊥x轴,连接OP,
∵P(﹣2,3),
∴PE=3,OE=2.
在Rt△OPE中,根据勾股定理得:OP2=PE2+OE2,
∴OP==,则点P在原点的距离为.
故选:B.
4.(3分)下列图形中,是轴对称图形的有( )
A.4个 B.3个 C.2个 D.1个
【分析】根据轴对称图形的概念求解,如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形.
【解答】解:第一,第三个图形,沿着一条直线翻折,直线两方的部分能够完全重合,所以是轴对称图形;
第二,第四个图形,找不到这样一条直线,翻折后使直线两方的部分能够完全重合,所以不是轴对称图形;
所以是轴对称图形的有2个,
故选:C.
5.(3分)下列各组数中,能作为直角三角形的三边长的是( )
A.4,5,6 B.6,8,11 C.5,22,24 D.7,24,25
【分析】根据三角形的三边关系定理和勾股定理的逆定理逐个判断.
【解答】解:A、42+52≠62,故不能构成直角三角形,故不符合题意;
B、62+62≠112,故不能构成直角三角形,故不符合题意;
C、52+222≠242,故不能构成直角三角形,故不符合题意;
D、72+242=252,故能构成直角三角形,故符合题意.
故选:D.
6.(3分)在平行四边形ABCD中,若∠A=115°,则∠D的度数是( )
A.105° B.115° C.125° D.65°
【分析】根据平行四边形的邻角互补即可解决问题.
【解答】解:∵四边形ABCD是平行四边形,
∴∠A+∠D=180°,
∴∠D=180°﹣115°=65°,
故选:D.
7.(3分)若正比例函数y=kx(k≠0)的图象过点(1,﹣2),则k的值是( )
A. B.2 C.﹣ D.﹣2
【分析】把点的坐标代入y=kx(k≠0)即可求出k的值.
【解答】解:∵正比例函数y=kx(k≠0)的图象过点(1,﹣2),
∴﹣2=k,
∴k=﹣2.
故选:D.
8.(3分)直线y=2x﹣4与两坐标轴所围成的三角形面积等于( )
A.2 B.4 C.6 D.8
【分析】根据题意易得此直线与坐标轴的两个交点坐标,该直线与坐标轴围成的三角形的面积等于×直线与x轴交点的横坐标的绝对值×直线与y轴交点的纵坐标.
【解答】解:当x=0时,y=﹣4,
当y=0时,x=2,
∴所求三角形的面积=×2×|﹣4|=4.
故选:B.
9.(3分)如图,菱形ABCD中,对角线AC、BD相交于点O,H为AD边的中点,菱形的周长为28,则OH的长为( )
A.3.5 B.4.5 C.7 D.14
【分析】由菱形的性质得AC⊥BD,AD=7,再由直角三角形斜边上的中线性质即可求解.
【解答】解:∵菱形ABCD的周长为28,
∴AC⊥BD,AB=BC=CD=AD=7,
∴∠AOD=90°,
∵H为AD边的中点,
∴OH=AD=3.5,
故选:A.
10.(3分)端午节期间,甲、乙两队举行了一年一度的赛龙舟比赛,两队在比赛时的路程s(米)与时间t(分钟)之间的函数关系如图所示,请你根据图象判断,下列说法正确的是( )
A.甲队率先到达终点
B.甲队比乙队多走了200米
C.乙队的速度始终比甲队的速度大
D.乙队比甲队少用0.2分钟
【分析】根据函数图象所给的信息,逐一判断.
【解答】解:A.由函数图象可知,甲走完全程需要4分钟,乙走完全程需要3.8分钟,乙队率先到达终点,本选项不合题意;
B.由函数图象可知,甲、乙两队都走了1000米,路程相同,本选项不合题意;
C.根据0~2.2分钟的时间段图象可知,甲队的速度比乙队的速度快,本选项不合题意;
D.因为4﹣3.8=0.2分钟,所以,乙队比甲队少用0.2分钟,此选项符合题意;
故选:D.
二、填空题(每小题3分,共计30分)
11.(3分)函数y=的自变量x的取值范围是 x≠3 .
【分析】根据分式有意义的条件列出不等式,解不等式即可.
【解答】解:根据题意得:x﹣3≠0,
∴x≠3,
故答案为:x≠3.
12.(3分)计算:5÷×= 1 .
【分析】根据二次根式的乘除法法则进行计算即可.
【解答】解:原式=×==1,
故答案为:1.
13.(3分)如图,把矩形ABCD沿EF折叠,若∠1=40°,则∠AEF= 110 °.
【分析】由AD∥BC,推出∠AEF+∠BFE=180°,求出∠BFE即可解决问题.
【解答】解:∵∠BFE=∠EFM,∠1=40°,
∴∠BFM=180°﹣40°=140°,
∴∠BFE=70°,
∵AD∥BC,
∴∠AEF+∠BFE=180°,
∴∠AEF=110°,
故答案为:110.
14.(3分)一次函数y=﹣2x+5的图象不经过第 三 象限.
【分析】根据一次函数的解析式和一次函数的性质,可以得到该函数的图象经过哪几个象限,不经过哪个象限.
【解答】解:∵一次函数y=﹣2x+5,k=﹣2<0,b=5>0,
∴该函数图象经过第一、二、四象限,不经过第三象限,
故答案为:三.
15.(3分)已知a、b为两个连续的整数,且,则a+b= 11 .
【分析】根据无理数的性质,得出接近无理数的整数,即可得出a,b的值,即可得出答案.
【解答】解:∵,a、b为两个连续的整数,
∴<<,
∴a=5,b=6,
∴a+b=11.
故答案为:11.
16.(3分)若一次函数y=(m﹣4)x+3中,y随x的增大而增大,则m的取值范围是 m>4 .
【分析】由一次函数的性质可得到关于m的不等式,可求得m的取值范围.
【解答】解:∵一次函数y=(m﹣4)x+3,若y随x的增大而增大,
∴m﹣4>0,
解得m>4,
故答案为:m>4.
17.(3分)如图,?ABCD中,AB=3,AD=5,对角线AC的垂直平分线交AD边于点E,则△CDE的周长为 8 .
【分析】由AC的垂直平分线交AD于E,易证得AE=CE,又由四边形ABCD是平行四边形,即可求得AD与DC的长,继而求得答案.
【解答】解:∵AC的垂直平分线交AD于E,
∴AE=CE,
∵四边形ABCD是平行四边形,
∴CD=AB=3,AD=BC=5,
∴△CDE的周长是:DE+DE+CE=DC+DE+AE=DC+AD=3+5=8.
故答案为:8.
18.(3分)已知△ABC中,∠A=30°,AB=4,BC=,则AC= 或3 .
【分析】根据三角形的高BD的位置,分两种情形讨论即可解决问题;
【解答】解:此题存在两种情况:
(1)当高BD在△ABC内时,
在Rt△ABD中,∵AB=4,∠A=30°,
∴BD=AB=2,AD=BD=2,
在Rt△BCD中,CD==,
∴AC=AD+CD=3
(2)当高BD在△ABC外时,AC′=AD﹣DC′=2﹣=
故答案为:或3.
19.(3分)如图,在?ABCD中,按以下步骤作图:①以C为圆心,以适当长为半径画弧,分别交BC,CD于M,N两点;②分别以M,N为圆心,以大于MN的长为半径画弧,两弧在∠BCD的内部交于点P;⑨连接CP并延长交AD于E.若AE=2,CE=6,∠B=60°,则ABCD的周长等于 28 .
【分析】首先证明△DEC是等边三角形,求出AD,DC即可解决问题.
【解答】解:由作图可知∠ECD=∠ECB,
∵四边形ABCD是平行四边形,
∴AD∥BC,∠B=∠D=60°,
∴∠DEC=∠ECB=∠ECD,
∴DE=DC,
∴△DEC是等边三角形,
∴DE=DC=EC=6,
∴AD=BC=8,AB=CD=6,
∴四边形ABCD的周长为28,
故答案为28.
20.(3分)已知矩形ABCD,点E在AD边上,DE>AE,连接BE,将△ABE沿着BE翻折得到△BFE,射线EF交BC于G,若点G为BC的中点,FG=1,DE=6,则BE长为 2 .
【分析】先设AE=EF=x,根据DE=6,FG=1,可得AD=BC=x+6,EG=x+1,再根据∠GEB=∠GBE,可得EG=BG,求出AE的长,再结合勾股定理求解.
【解答】解:∵四边形ABCD是矩形,
∴∠BAD=90°,AB=CD,AD=BC,
设AE=EF=x,
∵DE=6,FG=1,
∴AD=BC=x+6,EG=x+1,
∵点G为BC的中点,
∴BG=BC=,
由折叠可得∠AEB=∠GEB,
∵AD∥BC,
∴∠AEB=∠GBE,
∴∠GEB=∠GBE,
∴EG=BG,
∴x+1=,
解得x=4,
在Rt△BGF中,FG=1,BG=BC==5,
∴BF==2,
在Rt△BEF中,BF=2,EF=AE=4,
∴BE==2.
故答案为2.
三、解答题(本题60分,其中21题8分,22每题7分,23题7分,24题8分,25、26、27每题各10分)
21.(8分)计算:
(1)(﹣)﹣(+);
(2)(2+)(2﹣)÷.
【分析】(1)直接化简二次根式,进而合并同类二次根式得出答案;
(2)直接利用乘法公式化简,再利用二次根式的除法运算法则计算即可.
【解答】解:(1)原式=2﹣﹣﹣
=﹣;
(2)原式=[(2)2﹣()2]÷
=(12﹣6)÷
=6÷
=2.
22.(7分)如图所示,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫格点,以格点为顶点分别按下列要求画图,要求它的顶点均在格点上.
(1)在图①中画一个面积为10的正方形.
(2)在图②中画一个面积为12的菱形,并直接写出这个菱形的周长.
【分析】(1)作出边长为的正方形即可;
(2)作出对角线分别为4,6的菱形即可.
【解答】解:(1)如图①中,正方形ABCD即为所求;
(2)如图②中,菱形ABCD即为所求.
∵AB==,
∴菱形ABCD的周长为4.
23.(7分)高尔基说:“书是人类进步的阶梯”.某单位650名职工积极参加向贫困地区学校捐书活动,为了解职工的捐书量,采用随机抽样的方法抽取30名职工作为样本,对他们的捐书量进行统计,统计结果共有4本、5本、6本、7本、8本五类,分别用A、B、C、D、E表示,根据统计数据绘制成了如图所示的不完整的条形统计图,由图中给出的信息解答下列问题:
(1)通过计算补全条形统计图;
(2)直接写出这30名职工捐书本数的平均数、众数和中位数;
(3)估计该单位650名职工共捐书多少本?
【分析】(1)根据题目中的数据和条形统计图中的数据,可以计算出捐D类书的人数,从而可以将条形统计图补充完整;
(2)根据条形统计图中的数据,可以计算出平均数和中位数,写出众数;
(3)根据(2)中的平均数,可以计算出该单位650名职工共捐书多少本.
【解答】解:(1)捐D类书的有30﹣4﹣6﹣9﹣3=8(人),
补全的条形统计图如右图所示;
(2)=×(4×4+5×6+6×9+7×8+8×3)=6(本),
众数是6本,
中位数是(6+6)÷2=6(本),
即这30名职工捐书本数的平均数、众数和中位数分别为6本、6本、6本;
(3)650×6=3900(本),
答:估计该单位650名职工共捐书3900本.
24.(8分)已知:在平行四边形ABCD中,对角线AC与BD相交于点O,点E、F分别为OB、OD的中点,连接AE并延长至点G,使EG=AE,连接CF、CG.
(1)如图1,求证:EG=FC;
(2)如图2,连接BG、OG,在不添加任何辅助线的情况下,请直接写出图中的四个平行四边形,使写出每个平行四边形的面积都等于平行四边形ABCD面积的一半.
【分析】(1)由平行四边形的性质得AB=CD,AB∥CD,OB=OD,由平行线的性质得∠ABE=∠CDF,易证BE=DF,由SAS证得△ABE≌△CDF(SAS),得出AE=FC,即可得出结论;
(2)由平行四边形的性质得OA=OC,AB∥CD,AB=CD,S四边形ABCD=4S△ABO,易证AG、OB互相平分,则四边形ABGO是平行四边形,S四边形ABGO=2S△ABO=S四边形ABCD,易证OE是△ACG的中位线,则OE∥CG,易证四边形BOCG是平行四边形,S四边形BGCO=2S△BGO=2S△ABO=S四边形ABCD,证GO∥CD,GO=CD,则四边形CDOG是平行四边形,S四边形CDOG=2S△CDO=2S△ABO=S四边形ABCD,证CG∥EF,EF=CG,则四边形EFCG是平行四边形,S四边形EFCG=S四边形CDOG=S四边形ABCD.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,OB=OD,
∴∠ABE=∠CDF,
∵点E,F分别为OB,OD的中点,
∴BE=OB,DF=OD,
∴BE=DF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS),
∴AE=FC,
∵EG=AE,
∴EG=FC;
(2)解:∵四边形ABCD是平行四边形,
∴OA=OC,AB∥CD,AB=CD,S四边形ABCD=4S△ABO,
∵EG=AE,点E为OB的中点,
∴AG、OB互相平分,
∴四边形ABGO是平行四边形,
∴S△ABO=S△BGO,
∴S四边形ABGO=2S△ABO=S四边形ABCD,
∵OA=OC,EG=AE,
∴OE是△ACG的中位线,
∴OE∥CG,
∵四边形ABGO是平行四边形,
∴BG∥AC,
∴四边形BOCG是平行四边形,
∴S四边形BGCO=2S△BGO=2S△ABO=S四边形ABCD,
∵四边形ABGO是平行四边形,
∴GO∥AB,GO=AB,
∵AB∥CD,
∴GO∥CD,GO=CD,
∴四边形CDOG是平行四边形,
∴S四边形CDOG=2S△CDO=2S△ABO=S四边形ABCD,
∵点E,F分别为OB,OD的中点,
∴EF=BD=OD,
∵四边形CDOG是平行四边形,
∴CG∥EF,CG=OD,
∴EF=CG,
∴四边形EFCG是平行四边形,
∴S四边形EFCG=S四边形CDOG=S四边形ABCD,
∴图中的平行四边形ABGO、平行四边形BOCG、平行四边形CDOG、平行四边形EFCG四个平行四边形,每个平行四边形的面积都等于平行四边形ABCD面积的一半.
25.(10分)小俊奶茶店厂生产A.B两种奶茶,由于地处旅游景点区域,每天都供不应求.经过数学计算,小俊发现A种奶茶每杯生产时间为4分钟,B种奶茶每杯生产时间为1分钟,由于原料和运营时间限制,每天生产的总时间为300分钟.
(1)设A种奶茶生产x杯,B种奶茶生产y杯,则y与x之间的函数关系式y= y=﹣4x+300 .
(2)由于A种奶茶比较受顾客青睐,小俊决定每天生产A种奶茶不少于73杯,那么不同的生产方案有多少种?并写出每种生产方案.
(3)在(2)情况下,若A种奶茶每杯利润为3元,B种奶茶每杯利润为1元,直接写出小俊每天获得的最大利润为 227元 .
【分析】(1)依据每天生产的时间为300分钟列出函数关系式即可;
(2)由A种奶茶不少于73杯,B种奶茶的杯数为非负数列不等式组求解即可;
(3)列出利润与x的函数关系式,然后依据一次函数的性质求解即可.
【解答】解:(1)因为每天生产的时间为300分钟,所以4x+y=300,y=﹣4x+300;
故答案为:y=﹣4x+300.
(2)由题意得:,解得:73≤x≤75.
∵x为正整数,
∴x的值为73或74或75.
方案一:A种73杯,B种8杯
方案二:A种74杯,B种4杯
方案三:A种75杯,B种0杯.
(3)利润为:3x+(﹣4x+300)=﹣x+300
故生产A种奶茶73杯,B种奶茶8杯时,利润最大为227元.
故答案为:227元.
26.(10分)如图,四边形ABCD是正方形,点G是BC边上任意一点,DE⊥AG于点E,BF∥DE且交AG于点F.
(1)求证:AE=BF;
(2)如图2,连接DF、CE,探究线段DF与CE的关系并证明;
(3)图1中,若AB=8,BG=6,求EF长.
【分析】(1)根据AAS证△AED≌△BFA即可得出AE=BF;
(2)根据SAS证△ADF≌△DCE,可证DF=CE,根据∠ADF+∠CDF=90°,∠DCE+∠CDF=90°,得∠CFD=180°﹣(∠DCE+∠CDF)=180°﹣90°=90°,即可得证DF⊥CE;
(3)在Rt△ABG中,根据勾股定理可得:AG=10,面积法求出BF=,在Rt△ABF中,由勾股定理得:AF=,由EF=AF﹣AE即可得出EF的长度.
【解答】(1)证明:∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∴∠BAF+∠EAD=90°,
∵DE⊥AG,
∴∠AED=90°,
∴∠ADE+∠EAD=90°,
∴∠BAF=∠ADE,
∵BF∥DE,
∴∠AFB=∠DEA=90°,
在△AED和△BFA中,
∵,
∴△AED≌△BFA(AAS),
∴AE=BF;
(2)DF=CE,且DF⊥CE,证明如下:
由(1)知△AED≌△BFA,
∴DE=AF,
∵四边形ABCD是正方形,
∴AD=CD,∠ADC=90°,
∴∠ADE+∠EDC=90°,
∵DE⊥AG,
∴∠AED=90°,
∴∠DAF+∠ADE=90°,
∴∠EDC=∠EAD,
在△ADF和△DCE中,
∵,
∴△ADF≌△DCE(SAS)
∴DF=CE,∠ADF=∠DCE,
∵∠ADC=90°,
∴∠ADF+∠CDF=90°,
∴∠DCE+∠CDF=90°,
∴∠CFD=180°﹣(∠DCE+∠CDF)=180°﹣90°=90°,
∴DF⊥CE;
(3)∵四边形ABCD是正方形,
∴∠ABC=90°,
∵AB=8,BG=6,
在Rt△ABG中,根据勾股定理可得:
AG===10,
∵∠AFB=90°,
∴BF⊥AG,
∵AG×BF=AB×BG,
∴10×BF=8×6,
∴BF=,
由(1)知AE=BF,
∴AE=,
在Rt△ABF中,由勾股定理得:
AF===,
∴EF=AF﹣AE=﹣=.
27.(10分)如图1,平面直角坐标系中,直线y=﹣x+b交x轴于点A(8,0),交y轴正半轴于点B.
(1)求点B的坐标;
(2)如图2,直线BC交x轴负半轴于点C,且AB=AC,P为线段BC上一点,过点P作x轴的平行线交直线AB于点Q,设点P的横坐标为m,线段PQ的长为d,求d与m之间的函数关系式;
(3)在(2)的条件下,M为CB延长线上一点,且BM=CP,在线段AB上是否存在点N,使△PMN是以PM为斜边的等腰直角三角形,若存在,请求出点N的坐标;若不存在,请说明理由.
【分析】(1)利用待定系数法即可得到问题的答案;
(2)利用勾股定理得点C的坐标,设直线BC解析式为y=kx+6,利用待定系数法得解析式,根据点Q的位置可得答案;
(3)过点M 作MG⊥PQ于G,根据AAS得△BOC≌△MGP,由全等三角形的性质得PG=OC=2,GM=OB=6,过点N作NH⊥PQ于H,过点M作MR⊥NH于点R,根据矩形的判定与性质、等腰三角形的性质可得∠RNM=∠HPN,再由全等三角形的判定与性质可得HP=4,最后根据待定系数法可得答案.
【解答】解:(1)∵y=﹣x+b交x轴于点A(8,0),
∴0=﹣×8+b,b=6,
∴直线AB解析式为y=﹣x+6,令x=0,y=6,
∴B(0,6).
(2)∵A(8,0),B(0,6),
∴OA=8,OB=6,
∵∠AOB=90°,
∴AB==10=AC,
∴OC=2,
∴点C(﹣2,0),
设直线BC解析式为y=kx+6,
∴﹣2k+6=0,
∴k=3,
∴直线BC解析式为y=3x+6,
∵P在直线y=3x+6上,
∴可设点P(m,3m+6),
∵PQ∥x轴,且点Q在y=﹣x+6上,
∴Q(﹣4m,3m+6)
∴d=﹣4m﹣m=﹣5m,
(3)过点M 作MG⊥PQ于G,
∴∠PGM=90°=∠BOC,
∵PQ∥x轴,
∴∠OCB=∠GPM,
∵CP=BM,
∴BC=PM,
∴△BOC≌△MGP(AAS),
∴PG=OC=2,GM=OB=6,
过点N作NH⊥PQ于H,过点M作MR⊥NH于点R,
∴∠MGH=∠RHG=∠MRH=90°,
∴四边形GHRM是矩形,
∴HR=GM=6,
可设GH=RM=t,
∵△PMN是以PM为斜边的等腰直角三角形,
∴∠PNM=90°,PN=MN,
∴∠HNP+∠RNM=90°,
∵∠PHN=90°,
∴∠HNP+∠HPN=90°,
∴∠RNM=∠HPN,
∴Rt△PHN≌Rt△NRM(HL),
∴HN=RM=t,NR=PH=2+t,
∵HR=HN+NR,
∴t+2+t=6,
∴t=2,
∴GH=NH=RM=2,
∴HP=4,
∵P(m,3m+6),
∴N(m+4,3m+6+2)即N(m+4,3m+8),
∵N在直线y=﹣x+6上,
∴3m+8=﹣(m+4)+6,
∴m=﹣,P(﹣,2),N(,4).
一、填空题(每小题3分,共计30分)
1.(3分)下列运算正确的是( )
A.+= B.=7 C.÷=3 D.=﹣6
2.(3分)下列二次根式中,是最简二次根式的是( )
A. B. C. D.
3.(3分)在直角坐标系中,点P(﹣2,3)到原点的距离是( )
A. B. C. D.2
4.(3分)下列图形中,是轴对称图形的有( )
A.4个 B.3个 C.2个 D.1个
5.(3分)下列各组数中,能作为直角三角形的三边长的是( )
A.4,5,6 B.6,8,11 C.5,22,24 D.7,24,25
6.(3分)在平行四边形ABCD中,若∠A=115°,则∠D的度数是( )
A.105° B.115° C.125° D.65°
7.(3分)若正比例函数y=kx(k≠0)的图象过点(1,﹣2),则k的值是( )
A. B.2 C.﹣ D.﹣2
8.(3分)直线y=2x﹣4与两坐标轴所围成的三角形面积等于( )
A.2 B.4 C.6 D.8
9.(3分)如图,菱形ABCD中,对角线AC、BD相交于点O,H为AD边的中点,菱形的周长为28,则OH的长为( )
A.3.5 B.4.5 C.7 D.14
10.(3分)端午节期间,甲、乙两队举行了一年一度的赛龙舟比赛,两队在比赛时的路程s(米)与时间t(分钟)之间的函数关系如图所示,请你根据图象判断,下列说法正确的是( )
A.甲队率先到达终点
B.甲队比乙队多走了200米
C.乙队的速度始终比甲队的速度大
D.乙队比甲队少用0.2分钟
二、填空题(每小题3分,共计30分)
11.(3分)函数y=的自变量x的取值范围是 .
12.(3分)计算:5÷×= .
13.(3分)如图,把矩形ABCD沿EF折叠,若∠1=40°,则∠AEF= °.
14.(3分)一次函数y=﹣2x+5的图象不经过第 象限.
15.(3分)已知a、b为两个连续的整数,且,则a+b= .
16.(3分)若一次函数y=(m﹣4)x+3中,y随x的增大而增大,则m的取值范围是 .
17.(3分)如图,?ABCD中,AB=3,AD=5,对角线AC的垂直平分线交AD边于点E,则△CDE的周长为 .
18.(3分)已知△ABC中,∠A=30°,AB=4,BC=,则AC= .
19.(3分)如图,在?ABCD中,按以下步骤作图:①以C为圆心,以适当长为半径画弧,分别交BC,CD于M,N两点;②分别以M,N为圆心,以大于MN的长为半径画弧,两弧在∠BCD的内部交于点P;⑨连接CP并延长交AD于E.若AE=2,CE=6,∠B=60°,则ABCD的周长等于 .
20.(3分)已知矩形ABCD,点E在AD边上,DE>AE,连接BE,将△ABE沿着BE翻折得到△BFE,射线EF交BC于G,若点G为BC的中点,FG=1,DE=6,则BE长为 .
三、解答题(本题60分,其中21题8分,22每题7分,23题7分,24题8分,25、26、27每题各10分)
21.(8分)计算:
(1)(﹣)﹣(+);
(2)(2+)(2﹣)÷.
22.(7分)如图所示,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫格点,以格点为顶点分别按下列要求画图,要求它的顶点均在格点上.
(1)在图①中画一个面积为10的正方形.
(2)在图②中画一个面积为12的菱形,并直接写出这个菱形的周长.
23.(7分)高尔基说:“书是人类进步的阶梯”.某单位650名职工积极参加向贫困地区学校捐书活动,为了解职工的捐书量,采用随机抽样的方法抽取30名职工作为样本,对他们的捐书量进行统计,统计结果共有4本、5本、6本、7本、8本五类,分别用A、B、C、D、E表示,根据统计数据绘制成了如图所示的不完整的条形统计图,由图中给出的信息解答下列问题:
(1)通过计算补全条形统计图;
(2)直接写出这30名职工捐书本数的平均数、众数和中位数;
(3)估计该单位650名职工共捐书多少本?
24.(8分)已知:在平行四边形ABCD中,对角线AC与BD相交于点O,点E、F分别为OB、OD的中点,连接AE并延长至点G,使EG=AE,连接CF、CG.
(1)如图1,求证:EG=FC;
(2)如图2,连接BG、OG,在不添加任何辅助线的情况下,请直接写出图中的四个平行四边形,使写出每个平行四边形的面积都等于平行四边形ABCD面积的一半.
25.(10分)小俊奶茶店厂生产A.B两种奶茶,由于地处旅游景点区域,每天都供不应求.经过数学计算,小俊发现A种奶茶每杯生产时间为4分钟,B种奶茶每杯生产时间为1分钟,由于原料和运营时间限制,每天生产的总时间为300分钟.
(1)设A种奶茶生产x杯,B种奶茶生产y杯,则y与x之间的函数关系式y= .
(2)由于A种奶茶比较受顾客青睐,小俊决定每天生产A种奶茶不少于73杯,那么不同的生产方案有多少种?并写出每种生产方案.
(3)在(2)情况下,若A种奶茶每杯利润为3元,B种奶茶每杯利润为1元,直接写出小俊每天获得的最大利润为 .
26.(10分)如图,四边形ABCD是正方形,点G是BC边上任意一点,DE⊥AG于点E,BF∥DE且交AG于点F.
(1)求证:AE=BF;
(2)如图2,连接DF、CE,探究线段DF与CE的关系并证明;
(3)图1中,若AB=8,BG=6,求EF长.
27.(10分)如图1,平面直角坐标系中,直线y=﹣x+b交x轴于点A(8,0),交y轴正半轴于点B.
(1)求点B的坐标;
(2)如图2,直线BC交x轴负半轴于点C,且AB=AC,P为线段BC上一点,过点P作x轴的平行线交直线AB于点Q,设点P的横坐标为m,线段PQ的长为d,求d与m之间的函数关系式;
(3)在(2)的条件下,M为CB延长线上一点,且BM=CP,在线段AB上是否存在点N,使△PMN是以PM为斜边的等腰直角三角形,若存在,请求出点N的坐标;若不存在,请说明理由.
2020-2021学年黑龙江省哈尔滨市通河县八年级(下)期末数学试卷
参考答案与试题解析
一、填空题(每小题3分,共计30分)
1.(3分)下列运算正确的是( )
A.+= B.=7 C.÷=3 D.=﹣6
【分析】根据各个选项中的式子,可以计算出正确的结果,从而可以解答本题.
【解答】解:+不能合并,故选项A不符合题意;
===5,故选项B不符合题意;
==3,故选项C符合题意;
=6,故选项D不符合题意;
故选:C.
2.(3分)下列二次根式中,是最简二次根式的是( )
A. B. C. D.
【分析】A:应用算术平方根的算法进行求解即可得出答案;
B:应用最简二次根式的定义进行求解即可得出答案;
C:应用二次根式的乘法法则进行求解即可得出答案;
D:应用二次根式除法法则进行求解即可得出答案.
【解答】解:A:∵=3,∴A选项不符合题意;
B:∵是最简二次根式,∴B选项符合题意;
C:∵=3|a|,∴C选项不符合题意;
D:∵==,∴D选项不符合题意.
故选:B.
3.(3分)在直角坐标系中,点P(﹣2,3)到原点的距离是( )
A. B. C. D.2
【分析】在平面直角坐标系中找出P点,过P作PE垂直于x轴,连接OP,由P的坐标得出PE及OE的长,在直角三角形OPE中,由PE及OE的长,利用勾股定理求出OP的长,即为P到原点的距离.
【解答】解:过P作PE⊥x轴,连接OP,
∵P(﹣2,3),
∴PE=3,OE=2.
在Rt△OPE中,根据勾股定理得:OP2=PE2+OE2,
∴OP==,则点P在原点的距离为.
故选:B.
4.(3分)下列图形中,是轴对称图形的有( )
A.4个 B.3个 C.2个 D.1个
【分析】根据轴对称图形的概念求解,如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形.
【解答】解:第一,第三个图形,沿着一条直线翻折,直线两方的部分能够完全重合,所以是轴对称图形;
第二,第四个图形,找不到这样一条直线,翻折后使直线两方的部分能够完全重合,所以不是轴对称图形;
所以是轴对称图形的有2个,
故选:C.
5.(3分)下列各组数中,能作为直角三角形的三边长的是( )
A.4,5,6 B.6,8,11 C.5,22,24 D.7,24,25
【分析】根据三角形的三边关系定理和勾股定理的逆定理逐个判断.
【解答】解:A、42+52≠62,故不能构成直角三角形,故不符合题意;
B、62+62≠112,故不能构成直角三角形,故不符合题意;
C、52+222≠242,故不能构成直角三角形,故不符合题意;
D、72+242=252,故能构成直角三角形,故符合题意.
故选:D.
6.(3分)在平行四边形ABCD中,若∠A=115°,则∠D的度数是( )
A.105° B.115° C.125° D.65°
【分析】根据平行四边形的邻角互补即可解决问题.
【解答】解:∵四边形ABCD是平行四边形,
∴∠A+∠D=180°,
∴∠D=180°﹣115°=65°,
故选:D.
7.(3分)若正比例函数y=kx(k≠0)的图象过点(1,﹣2),则k的值是( )
A. B.2 C.﹣ D.﹣2
【分析】把点的坐标代入y=kx(k≠0)即可求出k的值.
【解答】解:∵正比例函数y=kx(k≠0)的图象过点(1,﹣2),
∴﹣2=k,
∴k=﹣2.
故选:D.
8.(3分)直线y=2x﹣4与两坐标轴所围成的三角形面积等于( )
A.2 B.4 C.6 D.8
【分析】根据题意易得此直线与坐标轴的两个交点坐标,该直线与坐标轴围成的三角形的面积等于×直线与x轴交点的横坐标的绝对值×直线与y轴交点的纵坐标.
【解答】解:当x=0时,y=﹣4,
当y=0时,x=2,
∴所求三角形的面积=×2×|﹣4|=4.
故选:B.
9.(3分)如图,菱形ABCD中,对角线AC、BD相交于点O,H为AD边的中点,菱形的周长为28,则OH的长为( )
A.3.5 B.4.5 C.7 D.14
【分析】由菱形的性质得AC⊥BD,AD=7,再由直角三角形斜边上的中线性质即可求解.
【解答】解:∵菱形ABCD的周长为28,
∴AC⊥BD,AB=BC=CD=AD=7,
∴∠AOD=90°,
∵H为AD边的中点,
∴OH=AD=3.5,
故选:A.
10.(3分)端午节期间,甲、乙两队举行了一年一度的赛龙舟比赛,两队在比赛时的路程s(米)与时间t(分钟)之间的函数关系如图所示,请你根据图象判断,下列说法正确的是( )
A.甲队率先到达终点
B.甲队比乙队多走了200米
C.乙队的速度始终比甲队的速度大
D.乙队比甲队少用0.2分钟
【分析】根据函数图象所给的信息,逐一判断.
【解答】解:A.由函数图象可知,甲走完全程需要4分钟,乙走完全程需要3.8分钟,乙队率先到达终点,本选项不合题意;
B.由函数图象可知,甲、乙两队都走了1000米,路程相同,本选项不合题意;
C.根据0~2.2分钟的时间段图象可知,甲队的速度比乙队的速度快,本选项不合题意;
D.因为4﹣3.8=0.2分钟,所以,乙队比甲队少用0.2分钟,此选项符合题意;
故选:D.
二、填空题(每小题3分,共计30分)
11.(3分)函数y=的自变量x的取值范围是 x≠3 .
【分析】根据分式有意义的条件列出不等式,解不等式即可.
【解答】解:根据题意得:x﹣3≠0,
∴x≠3,
故答案为:x≠3.
12.(3分)计算:5÷×= 1 .
【分析】根据二次根式的乘除法法则进行计算即可.
【解答】解:原式=×==1,
故答案为:1.
13.(3分)如图,把矩形ABCD沿EF折叠,若∠1=40°,则∠AEF= 110 °.
【分析】由AD∥BC,推出∠AEF+∠BFE=180°,求出∠BFE即可解决问题.
【解答】解:∵∠BFE=∠EFM,∠1=40°,
∴∠BFM=180°﹣40°=140°,
∴∠BFE=70°,
∵AD∥BC,
∴∠AEF+∠BFE=180°,
∴∠AEF=110°,
故答案为:110.
14.(3分)一次函数y=﹣2x+5的图象不经过第 三 象限.
【分析】根据一次函数的解析式和一次函数的性质,可以得到该函数的图象经过哪几个象限,不经过哪个象限.
【解答】解:∵一次函数y=﹣2x+5,k=﹣2<0,b=5>0,
∴该函数图象经过第一、二、四象限,不经过第三象限,
故答案为:三.
15.(3分)已知a、b为两个连续的整数,且,则a+b= 11 .
【分析】根据无理数的性质,得出接近无理数的整数,即可得出a,b的值,即可得出答案.
【解答】解:∵,a、b为两个连续的整数,
∴<<,
∴a=5,b=6,
∴a+b=11.
故答案为:11.
16.(3分)若一次函数y=(m﹣4)x+3中,y随x的增大而增大,则m的取值范围是 m>4 .
【分析】由一次函数的性质可得到关于m的不等式,可求得m的取值范围.
【解答】解:∵一次函数y=(m﹣4)x+3,若y随x的增大而增大,
∴m﹣4>0,
解得m>4,
故答案为:m>4.
17.(3分)如图,?ABCD中,AB=3,AD=5,对角线AC的垂直平分线交AD边于点E,则△CDE的周长为 8 .
【分析】由AC的垂直平分线交AD于E,易证得AE=CE,又由四边形ABCD是平行四边形,即可求得AD与DC的长,继而求得答案.
【解答】解:∵AC的垂直平分线交AD于E,
∴AE=CE,
∵四边形ABCD是平行四边形,
∴CD=AB=3,AD=BC=5,
∴△CDE的周长是:DE+DE+CE=DC+DE+AE=DC+AD=3+5=8.
故答案为:8.
18.(3分)已知△ABC中,∠A=30°,AB=4,BC=,则AC= 或3 .
【分析】根据三角形的高BD的位置,分两种情形讨论即可解决问题;
【解答】解:此题存在两种情况:
(1)当高BD在△ABC内时,
在Rt△ABD中,∵AB=4,∠A=30°,
∴BD=AB=2,AD=BD=2,
在Rt△BCD中,CD==,
∴AC=AD+CD=3
(2)当高BD在△ABC外时,AC′=AD﹣DC′=2﹣=
故答案为:或3.
19.(3分)如图,在?ABCD中,按以下步骤作图:①以C为圆心,以适当长为半径画弧,分别交BC,CD于M,N两点;②分别以M,N为圆心,以大于MN的长为半径画弧,两弧在∠BCD的内部交于点P;⑨连接CP并延长交AD于E.若AE=2,CE=6,∠B=60°,则ABCD的周长等于 28 .
【分析】首先证明△DEC是等边三角形,求出AD,DC即可解决问题.
【解答】解:由作图可知∠ECD=∠ECB,
∵四边形ABCD是平行四边形,
∴AD∥BC,∠B=∠D=60°,
∴∠DEC=∠ECB=∠ECD,
∴DE=DC,
∴△DEC是等边三角形,
∴DE=DC=EC=6,
∴AD=BC=8,AB=CD=6,
∴四边形ABCD的周长为28,
故答案为28.
20.(3分)已知矩形ABCD,点E在AD边上,DE>AE,连接BE,将△ABE沿着BE翻折得到△BFE,射线EF交BC于G,若点G为BC的中点,FG=1,DE=6,则BE长为 2 .
【分析】先设AE=EF=x,根据DE=6,FG=1,可得AD=BC=x+6,EG=x+1,再根据∠GEB=∠GBE,可得EG=BG,求出AE的长,再结合勾股定理求解.
【解答】解:∵四边形ABCD是矩形,
∴∠BAD=90°,AB=CD,AD=BC,
设AE=EF=x,
∵DE=6,FG=1,
∴AD=BC=x+6,EG=x+1,
∵点G为BC的中点,
∴BG=BC=,
由折叠可得∠AEB=∠GEB,
∵AD∥BC,
∴∠AEB=∠GBE,
∴∠GEB=∠GBE,
∴EG=BG,
∴x+1=,
解得x=4,
在Rt△BGF中,FG=1,BG=BC==5,
∴BF==2,
在Rt△BEF中,BF=2,EF=AE=4,
∴BE==2.
故答案为2.
三、解答题(本题60分,其中21题8分,22每题7分,23题7分,24题8分,25、26、27每题各10分)
21.(8分)计算:
(1)(﹣)﹣(+);
(2)(2+)(2﹣)÷.
【分析】(1)直接化简二次根式,进而合并同类二次根式得出答案;
(2)直接利用乘法公式化简,再利用二次根式的除法运算法则计算即可.
【解答】解:(1)原式=2﹣﹣﹣
=﹣;
(2)原式=[(2)2﹣()2]÷
=(12﹣6)÷
=6÷
=2.
22.(7分)如图所示,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫格点,以格点为顶点分别按下列要求画图,要求它的顶点均在格点上.
(1)在图①中画一个面积为10的正方形.
(2)在图②中画一个面积为12的菱形,并直接写出这个菱形的周长.
【分析】(1)作出边长为的正方形即可;
(2)作出对角线分别为4,6的菱形即可.
【解答】解:(1)如图①中,正方形ABCD即为所求;
(2)如图②中,菱形ABCD即为所求.
∵AB==,
∴菱形ABCD的周长为4.
23.(7分)高尔基说:“书是人类进步的阶梯”.某单位650名职工积极参加向贫困地区学校捐书活动,为了解职工的捐书量,采用随机抽样的方法抽取30名职工作为样本,对他们的捐书量进行统计,统计结果共有4本、5本、6本、7本、8本五类,分别用A、B、C、D、E表示,根据统计数据绘制成了如图所示的不完整的条形统计图,由图中给出的信息解答下列问题:
(1)通过计算补全条形统计图;
(2)直接写出这30名职工捐书本数的平均数、众数和中位数;
(3)估计该单位650名职工共捐书多少本?
【分析】(1)根据题目中的数据和条形统计图中的数据,可以计算出捐D类书的人数,从而可以将条形统计图补充完整;
(2)根据条形统计图中的数据,可以计算出平均数和中位数,写出众数;
(3)根据(2)中的平均数,可以计算出该单位650名职工共捐书多少本.
【解答】解:(1)捐D类书的有30﹣4﹣6﹣9﹣3=8(人),
补全的条形统计图如右图所示;
(2)=×(4×4+5×6+6×9+7×8+8×3)=6(本),
众数是6本,
中位数是(6+6)÷2=6(本),
即这30名职工捐书本数的平均数、众数和中位数分别为6本、6本、6本;
(3)650×6=3900(本),
答:估计该单位650名职工共捐书3900本.
24.(8分)已知:在平行四边形ABCD中,对角线AC与BD相交于点O,点E、F分别为OB、OD的中点,连接AE并延长至点G,使EG=AE,连接CF、CG.
(1)如图1,求证:EG=FC;
(2)如图2,连接BG、OG,在不添加任何辅助线的情况下,请直接写出图中的四个平行四边形,使写出每个平行四边形的面积都等于平行四边形ABCD面积的一半.
【分析】(1)由平行四边形的性质得AB=CD,AB∥CD,OB=OD,由平行线的性质得∠ABE=∠CDF,易证BE=DF,由SAS证得△ABE≌△CDF(SAS),得出AE=FC,即可得出结论;
(2)由平行四边形的性质得OA=OC,AB∥CD,AB=CD,S四边形ABCD=4S△ABO,易证AG、OB互相平分,则四边形ABGO是平行四边形,S四边形ABGO=2S△ABO=S四边形ABCD,易证OE是△ACG的中位线,则OE∥CG,易证四边形BOCG是平行四边形,S四边形BGCO=2S△BGO=2S△ABO=S四边形ABCD,证GO∥CD,GO=CD,则四边形CDOG是平行四边形,S四边形CDOG=2S△CDO=2S△ABO=S四边形ABCD,证CG∥EF,EF=CG,则四边形EFCG是平行四边形,S四边形EFCG=S四边形CDOG=S四边形ABCD.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,OB=OD,
∴∠ABE=∠CDF,
∵点E,F分别为OB,OD的中点,
∴BE=OB,DF=OD,
∴BE=DF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS),
∴AE=FC,
∵EG=AE,
∴EG=FC;
(2)解:∵四边形ABCD是平行四边形,
∴OA=OC,AB∥CD,AB=CD,S四边形ABCD=4S△ABO,
∵EG=AE,点E为OB的中点,
∴AG、OB互相平分,
∴四边形ABGO是平行四边形,
∴S△ABO=S△BGO,
∴S四边形ABGO=2S△ABO=S四边形ABCD,
∵OA=OC,EG=AE,
∴OE是△ACG的中位线,
∴OE∥CG,
∵四边形ABGO是平行四边形,
∴BG∥AC,
∴四边形BOCG是平行四边形,
∴S四边形BGCO=2S△BGO=2S△ABO=S四边形ABCD,
∵四边形ABGO是平行四边形,
∴GO∥AB,GO=AB,
∵AB∥CD,
∴GO∥CD,GO=CD,
∴四边形CDOG是平行四边形,
∴S四边形CDOG=2S△CDO=2S△ABO=S四边形ABCD,
∵点E,F分别为OB,OD的中点,
∴EF=BD=OD,
∵四边形CDOG是平行四边形,
∴CG∥EF,CG=OD,
∴EF=CG,
∴四边形EFCG是平行四边形,
∴S四边形EFCG=S四边形CDOG=S四边形ABCD,
∴图中的平行四边形ABGO、平行四边形BOCG、平行四边形CDOG、平行四边形EFCG四个平行四边形,每个平行四边形的面积都等于平行四边形ABCD面积的一半.
25.(10分)小俊奶茶店厂生产A.B两种奶茶,由于地处旅游景点区域,每天都供不应求.经过数学计算,小俊发现A种奶茶每杯生产时间为4分钟,B种奶茶每杯生产时间为1分钟,由于原料和运营时间限制,每天生产的总时间为300分钟.
(1)设A种奶茶生产x杯,B种奶茶生产y杯,则y与x之间的函数关系式y= y=﹣4x+300 .
(2)由于A种奶茶比较受顾客青睐,小俊决定每天生产A种奶茶不少于73杯,那么不同的生产方案有多少种?并写出每种生产方案.
(3)在(2)情况下,若A种奶茶每杯利润为3元,B种奶茶每杯利润为1元,直接写出小俊每天获得的最大利润为 227元 .
【分析】(1)依据每天生产的时间为300分钟列出函数关系式即可;
(2)由A种奶茶不少于73杯,B种奶茶的杯数为非负数列不等式组求解即可;
(3)列出利润与x的函数关系式,然后依据一次函数的性质求解即可.
【解答】解:(1)因为每天生产的时间为300分钟,所以4x+y=300,y=﹣4x+300;
故答案为:y=﹣4x+300.
(2)由题意得:,解得:73≤x≤75.
∵x为正整数,
∴x的值为73或74或75.
方案一:A种73杯,B种8杯
方案二:A种74杯,B种4杯
方案三:A种75杯,B种0杯.
(3)利润为:3x+(﹣4x+300)=﹣x+300
故生产A种奶茶73杯,B种奶茶8杯时,利润最大为227元.
故答案为:227元.
26.(10分)如图,四边形ABCD是正方形,点G是BC边上任意一点,DE⊥AG于点E,BF∥DE且交AG于点F.
(1)求证:AE=BF;
(2)如图2,连接DF、CE,探究线段DF与CE的关系并证明;
(3)图1中,若AB=8,BG=6,求EF长.
【分析】(1)根据AAS证△AED≌△BFA即可得出AE=BF;
(2)根据SAS证△ADF≌△DCE,可证DF=CE,根据∠ADF+∠CDF=90°,∠DCE+∠CDF=90°,得∠CFD=180°﹣(∠DCE+∠CDF)=180°﹣90°=90°,即可得证DF⊥CE;
(3)在Rt△ABG中,根据勾股定理可得:AG=10,面积法求出BF=,在Rt△ABF中,由勾股定理得:AF=,由EF=AF﹣AE即可得出EF的长度.
【解答】(1)证明:∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∴∠BAF+∠EAD=90°,
∵DE⊥AG,
∴∠AED=90°,
∴∠ADE+∠EAD=90°,
∴∠BAF=∠ADE,
∵BF∥DE,
∴∠AFB=∠DEA=90°,
在△AED和△BFA中,
∵,
∴△AED≌△BFA(AAS),
∴AE=BF;
(2)DF=CE,且DF⊥CE,证明如下:
由(1)知△AED≌△BFA,
∴DE=AF,
∵四边形ABCD是正方形,
∴AD=CD,∠ADC=90°,
∴∠ADE+∠EDC=90°,
∵DE⊥AG,
∴∠AED=90°,
∴∠DAF+∠ADE=90°,
∴∠EDC=∠EAD,
在△ADF和△DCE中,
∵,
∴△ADF≌△DCE(SAS)
∴DF=CE,∠ADF=∠DCE,
∵∠ADC=90°,
∴∠ADF+∠CDF=90°,
∴∠DCE+∠CDF=90°,
∴∠CFD=180°﹣(∠DCE+∠CDF)=180°﹣90°=90°,
∴DF⊥CE;
(3)∵四边形ABCD是正方形,
∴∠ABC=90°,
∵AB=8,BG=6,
在Rt△ABG中,根据勾股定理可得:
AG===10,
∵∠AFB=90°,
∴BF⊥AG,
∵AG×BF=AB×BG,
∴10×BF=8×6,
∴BF=,
由(1)知AE=BF,
∴AE=,
在Rt△ABF中,由勾股定理得:
AF===,
∴EF=AF﹣AE=﹣=.
27.(10分)如图1,平面直角坐标系中,直线y=﹣x+b交x轴于点A(8,0),交y轴正半轴于点B.
(1)求点B的坐标;
(2)如图2,直线BC交x轴负半轴于点C,且AB=AC,P为线段BC上一点,过点P作x轴的平行线交直线AB于点Q,设点P的横坐标为m,线段PQ的长为d,求d与m之间的函数关系式;
(3)在(2)的条件下,M为CB延长线上一点,且BM=CP,在线段AB上是否存在点N,使△PMN是以PM为斜边的等腰直角三角形,若存在,请求出点N的坐标;若不存在,请说明理由.
【分析】(1)利用待定系数法即可得到问题的答案;
(2)利用勾股定理得点C的坐标,设直线BC解析式为y=kx+6,利用待定系数法得解析式,根据点Q的位置可得答案;
(3)过点M 作MG⊥PQ于G,根据AAS得△BOC≌△MGP,由全等三角形的性质得PG=OC=2,GM=OB=6,过点N作NH⊥PQ于H,过点M作MR⊥NH于点R,根据矩形的判定与性质、等腰三角形的性质可得∠RNM=∠HPN,再由全等三角形的判定与性质可得HP=4,最后根据待定系数法可得答案.
【解答】解:(1)∵y=﹣x+b交x轴于点A(8,0),
∴0=﹣×8+b,b=6,
∴直线AB解析式为y=﹣x+6,令x=0,y=6,
∴B(0,6).
(2)∵A(8,0),B(0,6),
∴OA=8,OB=6,
∵∠AOB=90°,
∴AB==10=AC,
∴OC=2,
∴点C(﹣2,0),
设直线BC解析式为y=kx+6,
∴﹣2k+6=0,
∴k=3,
∴直线BC解析式为y=3x+6,
∵P在直线y=3x+6上,
∴可设点P(m,3m+6),
∵PQ∥x轴,且点Q在y=﹣x+6上,
∴Q(﹣4m,3m+6)
∴d=﹣4m﹣m=﹣5m,
(3)过点M 作MG⊥PQ于G,
∴∠PGM=90°=∠BOC,
∵PQ∥x轴,
∴∠OCB=∠GPM,
∵CP=BM,
∴BC=PM,
∴△BOC≌△MGP(AAS),
∴PG=OC=2,GM=OB=6,
过点N作NH⊥PQ于H,过点M作MR⊥NH于点R,
∴∠MGH=∠RHG=∠MRH=90°,
∴四边形GHRM是矩形,
∴HR=GM=6,
可设GH=RM=t,
∵△PMN是以PM为斜边的等腰直角三角形,
∴∠PNM=90°,PN=MN,
∴∠HNP+∠RNM=90°,
∵∠PHN=90°,
∴∠HNP+∠HPN=90°,
∴∠RNM=∠HPN,
∴Rt△PHN≌Rt△NRM(HL),
∴HN=RM=t,NR=PH=2+t,
∵HR=HN+NR,
∴t+2+t=6,
∴t=2,
∴GH=NH=RM=2,
∴HP=4,
∵P(m,3m+6),
∴N(m+4,3m+6+2)即N(m+4,3m+8),
∵N在直线y=﹣x+6上,
∴3m+8=﹣(m+4)+6,
∴m=﹣,P(﹣,2),N(,4).
同课章节目录
