考前最后一轮基础知识巩固之第十一章 第2课 总体分布的估计
文档属性
| 名称 | 考前最后一轮基础知识巩固之第十一章 第2课 总体分布的估计 |
|
|
| 格式 | zip | ||
| 文件大小 | 76.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | |||
| 科目 | 数学 | ||
| 更新时间 | 2012-06-04 00:00:00 | ||
图片预览


文档简介
第2课 总体分布的估计
【考点导读】
1.掌握频率分布直方图、折线图表与茎叶图的做法,体会它们各自的特点.
2.会用频率分布直方图、折线图表与茎叶图对总体分布规律进行估计.
【基础练习】
1.一个容量为n的样本,分成若干组,已知某组的频数和频率分别为60,0.25,则n的值是 240 .
2.用样本频率分布估计总体频率分布的过程中,下列说法正确的是 ③ .
① 总体容量越大,估计越精确 ②总体容量越小,估计越精确
③ 样本容量越大,估计越精确 ④ 样本容量越小,估计越精确
10111213 780222366677800122344667880234
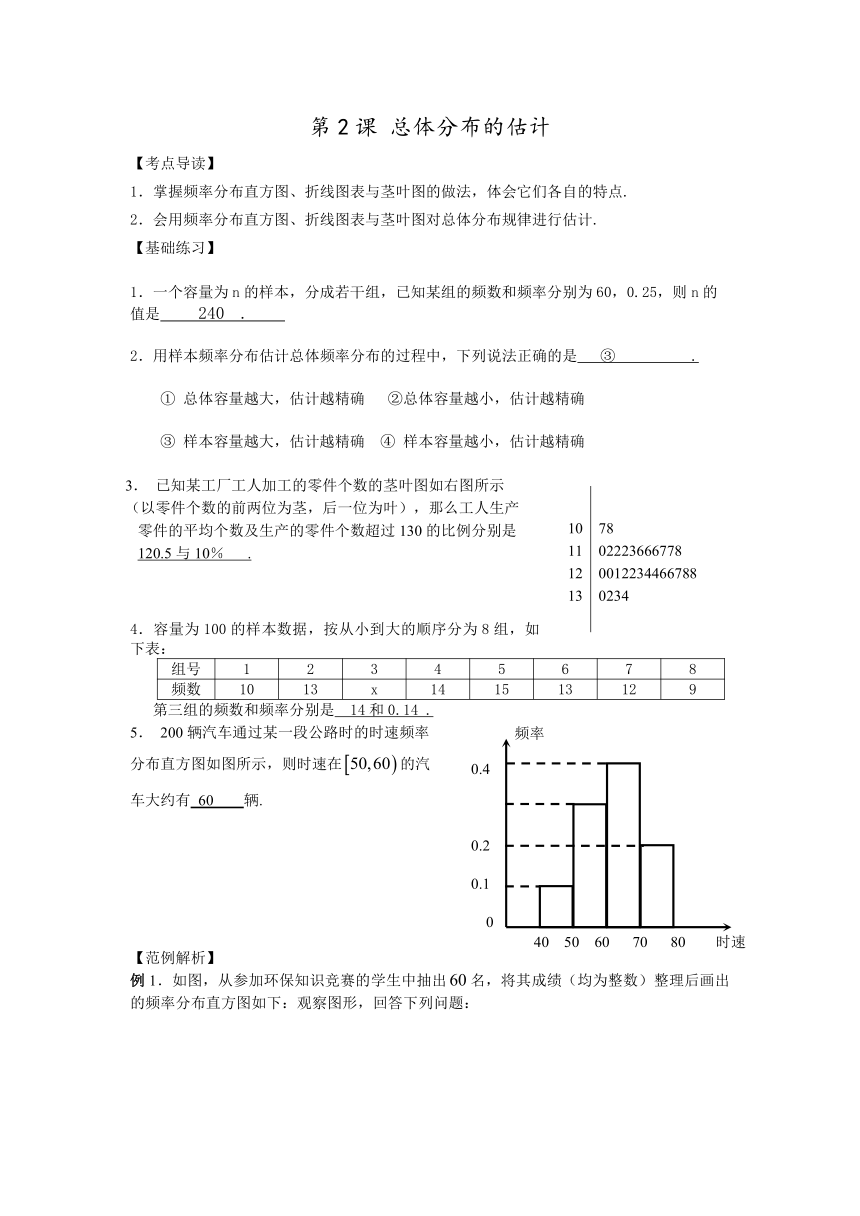
3. 已知某工厂工人加工的零件个数的茎叶图如右图所示
(以零件个数的前两位为茎,后一位为叶),那么工人生产
零件的平均个数及生产的零件个数超过130的比例分别是
120.5与10% .
4.容量为100的样本数据,按从小到大的顺序分为8组,如下表:
组号 1 2 3 4 5 6 7 8
频数 10 13 x 14 15 13 12 9
第三组的频数和频率分别是 14和0.14 .
5. 200辆汽车通过某一段公路时的时速频率
分布直方图如图所示,则时速在的汽
车大约有 60 辆.
【范例解析】
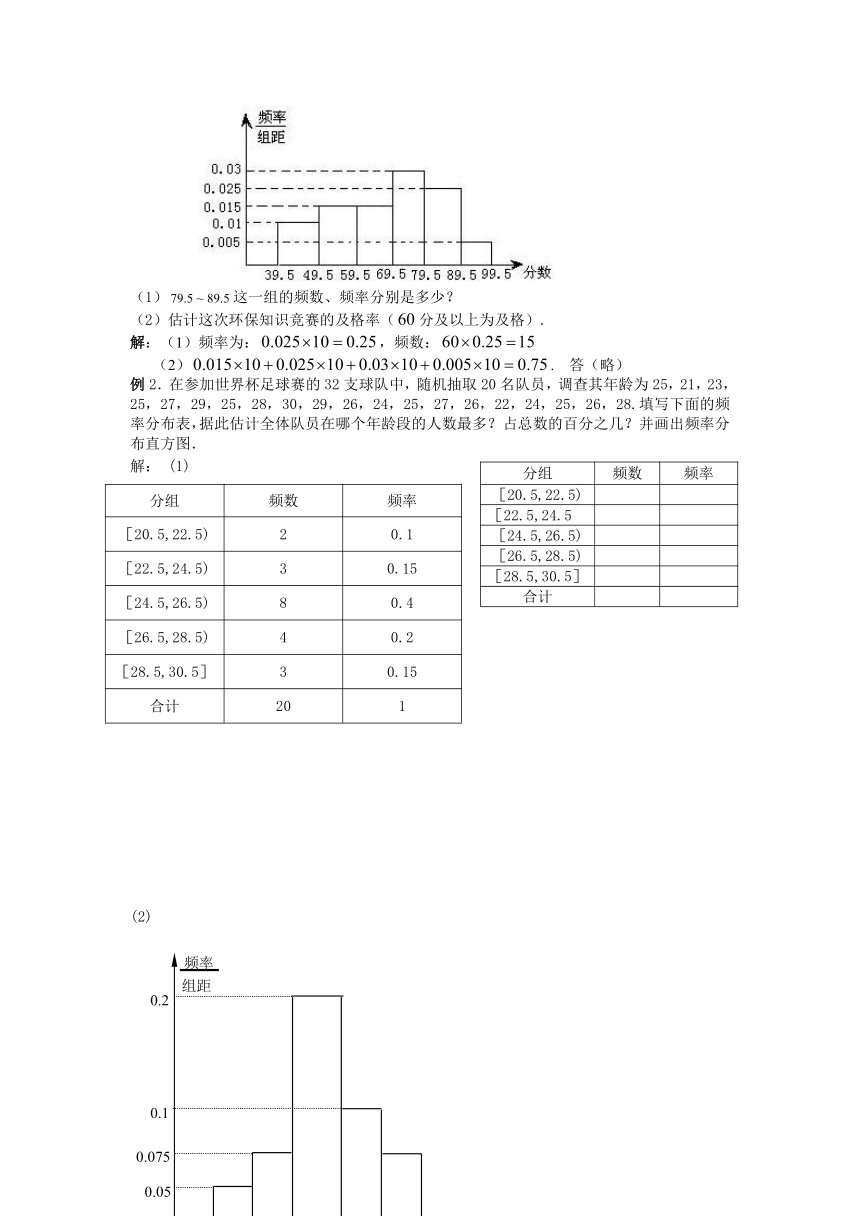
例1.如图,从参加环保知识竞赛的学生中抽出名,将其成绩(均为整数)整理后画出的频率分布直方图如下:观察图形,回答下列问题:
(1)这一组的频数、频率分别是多少?
(2)估计这次环保知识竞赛的及格率(分及以上为及格).
解:(1)频率为:,频数:
(2). 答(略)
例2.在参加世界杯足球赛的32支球队中,随机抽取20名队员,调查其年龄为25,21,23,25,27,29,25,28,30,29,26,24,25,27,26,22,24,25,26,28.填写下面的频率分布表,据此估计全体队员在哪个年龄段的人数最多?占总数的百分之几?并画出频率分布直方图.
分组 频数 频率
[20.5,22.5)
[22.5,24.5
[24.5,26.5)
[26.5,28.5)
[28.5,30.5]
合计
解: (1)
分组 频数 频率
[20.5,22.5) 2 0.1
[22.5,24.5) 3 0.15
[24.5,26.5) 8 0.4
[26.5,28.5) 4 0.2
[28.5,30.5] 3 0.15
合计 20 1
(2)
(3)估计全体队员在24.5~26.5处人数最多,占总数的百分之四十.
例3.为了了解高一学生的体能情况, 某校抽取部分
学生进行一分钟跳绳次数次测试,将所得数据整理
后,画出频率分布直方图(如图),图中从左到右
各小长方形面积之比为2:4:17:15:9:3,
第二小组频数为12.
第二小组的频率是多少?样本容量是多少?
若次数在110以上(含110次)为达标,试估计该学校全体高一学生的达标率是多少?
在这次测试中,学生跳绳次数的中位数落在哪个小组内?请说明理由.
分析:在频率分布直方图中,各小长方形的面积等于相应各组的频率,小长方形的高与频数成正比,各组频数之和等于样本容量,频率之和等于1.
解:(1)由于频率分布直方图以面积的形式反映了数据落在各小组内的频率大小,
因此第二小组的频率为:
又因为频率=
所以
(2)由图可估计该学校高一学生的达标率约为
(3)由已知可得各小组的频数依次为6,12,51,45,27,9,所以前三组的频数之和为69,前四组的频数之和为114,所以跳绳次数的中位数落在第四小组内.
【反馈演练】
1.对于样本频率直方图与总体密度曲线的关系,下列说法正确的是 ④
①频率分布直方图与总体密度曲线无关 ②频率分布直方图就是总体密度曲线
③样本容量很大的频率分布直方图就是总体密度曲线
④如果样本容量无限增大,分组的组距无限的减小,那么频率分布直方图就会无限接近于总体密度曲线
2. 在某餐厅内抽取100人,其中有30人在15岁以下,35人在16至25岁,25人在26至45岁,10人在46岁以上,则数 0.35 是16到25岁人员占总体分布的 ②
① 概率 ②频率 ③ 累计频率 ④ 频数
3.10名工人某天生产同一零件,生产的件数是 15 ,17 , 14 , 10 , 15 , 17 ,17 , 16, 14 , 12.
设其平均数为a,中位数为b,众数为c,则a, b, c的大小关系为
4.已知样本:10,8,6,10,13,8,10,12,11,7,8,9,11,9,12,9,10,11,12,12则频率为0.3的范围是 ( 2 )
5.已知10个数据如下:63,65,67,69,66,64,66, 64, 65,68.根据这些数据制作频率直方图,其中[64.5, 66.5)这组所对应矩形的高为 0.2
6.某中学高一年级有400人,高二年级有320人,高三有280人,以每人被抽取的频率为0.2,向该中学抽取一个样本容量为n的样本,则n= 200
7. 一个容量为20的样本数据,分组后,组距与频数如下: ,2; , 3 ; , 4 ; , 5 ; , 4 ; , 2 .则样本在区间 上的频率为__ 0.7 _______________
8.观察新生婴儿的体重,其频率分布直方图如图所示,则新生婴儿体重在的频率为 0.3
9.某校为了了解学生的课外阅读情况,随机调查了50名学生,得到他们在某一天各自课外阅读所用时间的数据,结果用右上面的条形图表示. 根据条形图可得这50名学生这一天平均每人的课外阅读时间为 0.9小时
10.从甲、乙两台机器生产的零件中随机抽取15个进行检验,相关指标的检验结果为:
甲:534,517,528,522,513,516,527,526,520,508,533,524,518,522,512;
乙:512,520,523,516,530,510,518,521,528,532,507,516,524,526,514.
(1).画出上述数据茎叶图;
(2).试比较分析甲、乙两台机器生产零件的情况.
解(1)用指标的两位数作茎,然后作茎叶图:
(2)从图中可以看出,甲机器生产零件的指标
分布大致对称,指标平均在520左右,中位数
和众数均为522;乙机器生产零件的指标分布为
大致对称,指标平均在520左右,中位数和众数
分别为520和516,总的来看,甲机器生产的零
件的指标略大些.
点评 注意作茎叶图时,茎可以放两位数.
11. 为了检测某种产品的质量,抽取了一个容量为100的样本,数据的分组数如下:
;;;;;;;;;
(1)列出频率分布表(含累积频率);
(2)画出频率分布直方图以及频率分布折线图;
(3)据上述图表,估计数据落在范围内的可能性是百分之几?
(4)数据小于11.20的可能性是百分之几?
[解]:(1)画出频率分布表
分组 频数 频率 累积频率
[10.75,10.85) 3 0.03 0.03
[10.85,10.95) 9 0.09 0.12
[10.95,11.05) 13 0.13 0.25
[11.05,11.15) 16 0.16 0.41
[11.15,11.25) 26 0.26 0.67
[11.25,11.35) 20 0.20 0.87
[11.35,11.45) 7 0.07 0.94
[11.45,11.55) 4 0.04 0.98
[11.55,11.65] 2 0.02 1.00
合计 100 1.00
(2)
(3)由上述图表可知数据落在范围内的频率为:,即数据落在范围内的可能性是75%.
(4)数据小于11.20的可能性即数据小于11.20的频率,也就是数据在11.20处的累积频率.设为,则:,
所以,从而估计数据小于11.20的可能性是54%.
频率
0.4
0.2
0.1
0
40 50 60 70 80 时速
年龄
频率
组距
20.5 22.5 24.5 26.5 28.5 30.5
0.05
0.075
0.1
0.2
90
100
110
120
130
140
150
次数
o
0.004
0.008
0.012
0.016
0.020
0.024
0.028
频率/组距
0.032
0.036
0.5
人数(人)
时间(小时)
20
10
5
0
1.0
1.5
2.0
15
(第9题)
(第8题)
2400 2700 3000 3300 3600 3900 体重
0
0 001
频率/组距
8
87632
87642200
43
50
51
52
53
7
024668
013468
02
频率/组距
1
2
3
产品质量
10.75 10.85 10.95 11.05 11.15 11.25 11.35 11.45 11.55 11.65
【考点导读】
1.掌握频率分布直方图、折线图表与茎叶图的做法,体会它们各自的特点.
2.会用频率分布直方图、折线图表与茎叶图对总体分布规律进行估计.
【基础练习】
1.一个容量为n的样本,分成若干组,已知某组的频数和频率分别为60,0.25,则n的值是 240 .
2.用样本频率分布估计总体频率分布的过程中,下列说法正确的是 ③ .
① 总体容量越大,估计越精确 ②总体容量越小,估计越精确
③ 样本容量越大,估计越精确 ④ 样本容量越小,估计越精确
10111213 780222366677800122344667880234
3. 已知某工厂工人加工的零件个数的茎叶图如右图所示
(以零件个数的前两位为茎,后一位为叶),那么工人生产
零件的平均个数及生产的零件个数超过130的比例分别是
120.5与10% .
4.容量为100的样本数据,按从小到大的顺序分为8组,如下表:
组号 1 2 3 4 5 6 7 8
频数 10 13 x 14 15 13 12 9
第三组的频数和频率分别是 14和0.14 .
5. 200辆汽车通过某一段公路时的时速频率
分布直方图如图所示,则时速在的汽
车大约有 60 辆.
【范例解析】
例1.如图,从参加环保知识竞赛的学生中抽出名,将其成绩(均为整数)整理后画出的频率分布直方图如下:观察图形,回答下列问题:
(1)这一组的频数、频率分别是多少?
(2)估计这次环保知识竞赛的及格率(分及以上为及格).
解:(1)频率为:,频数:
(2). 答(略)
例2.在参加世界杯足球赛的32支球队中,随机抽取20名队员,调查其年龄为25,21,23,25,27,29,25,28,30,29,26,24,25,27,26,22,24,25,26,28.填写下面的频率分布表,据此估计全体队员在哪个年龄段的人数最多?占总数的百分之几?并画出频率分布直方图.
分组 频数 频率
[20.5,22.5)
[22.5,24.5
[24.5,26.5)
[26.5,28.5)
[28.5,30.5]
合计
解: (1)
分组 频数 频率
[20.5,22.5) 2 0.1
[22.5,24.5) 3 0.15
[24.5,26.5) 8 0.4
[26.5,28.5) 4 0.2
[28.5,30.5] 3 0.15
合计 20 1
(2)
(3)估计全体队员在24.5~26.5处人数最多,占总数的百分之四十.
例3.为了了解高一学生的体能情况, 某校抽取部分
学生进行一分钟跳绳次数次测试,将所得数据整理
后,画出频率分布直方图(如图),图中从左到右
各小长方形面积之比为2:4:17:15:9:3,
第二小组频数为12.
第二小组的频率是多少?样本容量是多少?
若次数在110以上(含110次)为达标,试估计该学校全体高一学生的达标率是多少?
在这次测试中,学生跳绳次数的中位数落在哪个小组内?请说明理由.
分析:在频率分布直方图中,各小长方形的面积等于相应各组的频率,小长方形的高与频数成正比,各组频数之和等于样本容量,频率之和等于1.
解:(1)由于频率分布直方图以面积的形式反映了数据落在各小组内的频率大小,
因此第二小组的频率为:
又因为频率=
所以
(2)由图可估计该学校高一学生的达标率约为
(3)由已知可得各小组的频数依次为6,12,51,45,27,9,所以前三组的频数之和为69,前四组的频数之和为114,所以跳绳次数的中位数落在第四小组内.
【反馈演练】
1.对于样本频率直方图与总体密度曲线的关系,下列说法正确的是 ④
①频率分布直方图与总体密度曲线无关 ②频率分布直方图就是总体密度曲线
③样本容量很大的频率分布直方图就是总体密度曲线
④如果样本容量无限增大,分组的组距无限的减小,那么频率分布直方图就会无限接近于总体密度曲线
2. 在某餐厅内抽取100人,其中有30人在15岁以下,35人在16至25岁,25人在26至45岁,10人在46岁以上,则数 0.35 是16到25岁人员占总体分布的 ②
① 概率 ②频率 ③ 累计频率 ④ 频数
3.10名工人某天生产同一零件,生产的件数是 15 ,17 , 14 , 10 , 15 , 17 ,17 , 16, 14 , 12.
设其平均数为a,中位数为b,众数为c,则a, b, c的大小关系为
4.已知样本:10,8,6,10,13,8,10,12,11,7,8,9,11,9,12,9,10,11,12,12则频率为0.3的范围是 ( 2 )
5.已知10个数据如下:63,65,67,69,66,64,66, 64, 65,68.根据这些数据制作频率直方图,其中[64.5, 66.5)这组所对应矩形的高为 0.2
6.某中学高一年级有400人,高二年级有320人,高三有280人,以每人被抽取的频率为0.2,向该中学抽取一个样本容量为n的样本,则n= 200
7. 一个容量为20的样本数据,分组后,组距与频数如下: ,2; , 3 ; , 4 ; , 5 ; , 4 ; , 2 .则样本在区间 上的频率为__ 0.7 _______________
8.观察新生婴儿的体重,其频率分布直方图如图所示,则新生婴儿体重在的频率为 0.3
9.某校为了了解学生的课外阅读情况,随机调查了50名学生,得到他们在某一天各自课外阅读所用时间的数据,结果用右上面的条形图表示. 根据条形图可得这50名学生这一天平均每人的课外阅读时间为 0.9小时
10.从甲、乙两台机器生产的零件中随机抽取15个进行检验,相关指标的检验结果为:
甲:534,517,528,522,513,516,527,526,520,508,533,524,518,522,512;
乙:512,520,523,516,530,510,518,521,528,532,507,516,524,526,514.
(1).画出上述数据茎叶图;
(2).试比较分析甲、乙两台机器生产零件的情况.
解(1)用指标的两位数作茎,然后作茎叶图:
(2)从图中可以看出,甲机器生产零件的指标
分布大致对称,指标平均在520左右,中位数
和众数均为522;乙机器生产零件的指标分布为
大致对称,指标平均在520左右,中位数和众数
分别为520和516,总的来看,甲机器生产的零
件的指标略大些.
点评 注意作茎叶图时,茎可以放两位数.
11. 为了检测某种产品的质量,抽取了一个容量为100的样本,数据的分组数如下:
;;;;;;;;;
(1)列出频率分布表(含累积频率);
(2)画出频率分布直方图以及频率分布折线图;
(3)据上述图表,估计数据落在范围内的可能性是百分之几?
(4)数据小于11.20的可能性是百分之几?
[解]:(1)画出频率分布表
分组 频数 频率 累积频率
[10.75,10.85) 3 0.03 0.03
[10.85,10.95) 9 0.09 0.12
[10.95,11.05) 13 0.13 0.25
[11.05,11.15) 16 0.16 0.41
[11.15,11.25) 26 0.26 0.67
[11.25,11.35) 20 0.20 0.87
[11.35,11.45) 7 0.07 0.94
[11.45,11.55) 4 0.04 0.98
[11.55,11.65] 2 0.02 1.00
合计 100 1.00
(2)
(3)由上述图表可知数据落在范围内的频率为:,即数据落在范围内的可能性是75%.
(4)数据小于11.20的可能性即数据小于11.20的频率,也就是数据在11.20处的累积频率.设为,则:,
所以,从而估计数据小于11.20的可能性是54%.
频率
0.4
0.2
0.1
0
40 50 60 70 80 时速
年龄
频率
组距
20.5 22.5 24.5 26.5 28.5 30.5
0.05
0.075
0.1
0.2
90
100
110
120
130
140
150
次数
o
0.004
0.008
0.012
0.016
0.020
0.024
0.028
频率/组距
0.032
0.036
0.5
人数(人)
时间(小时)
20
10
5
0
1.0
1.5
2.0
15
(第9题)
(第8题)
2400 2700 3000 3300 3600 3900 体重
0
0 001
频率/组距
8
87632
87642200
43
50
51
52
53
7
024668
013468
02
频率/组距
1
2
3
产品质量
10.75 10.85 10.95 11.05 11.15 11.25 11.35 11.45 11.55 11.65
同课章节目录
