考前最后一轮基础知识巩固之第十章 第2课 流程图
文档属性
| 名称 | 考前最后一轮基础知识巩固之第十章 第2课 流程图 |  | |
| 格式 | zip | ||
| 文件大小 | 73.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | |||
| 科目 | 数学 | ||
| 更新时间 | 2012-06-04 15:33:03 | ||
图片预览

文档简介
第2课 流程图
【考点导读】
了解常用流程图符号的意义,能用流程图表示顺序,选择,循环这三种基本结构,并能识别简单的流程图所描述的算法.高考要求对流程图有最基本的认识,并能解决相关的简单问题.
【基础练习】
1.算法的三种基本结构是 顺序结构、选择结构、循环结构 .
2.流程图中表示判断框的是 菱形框 .
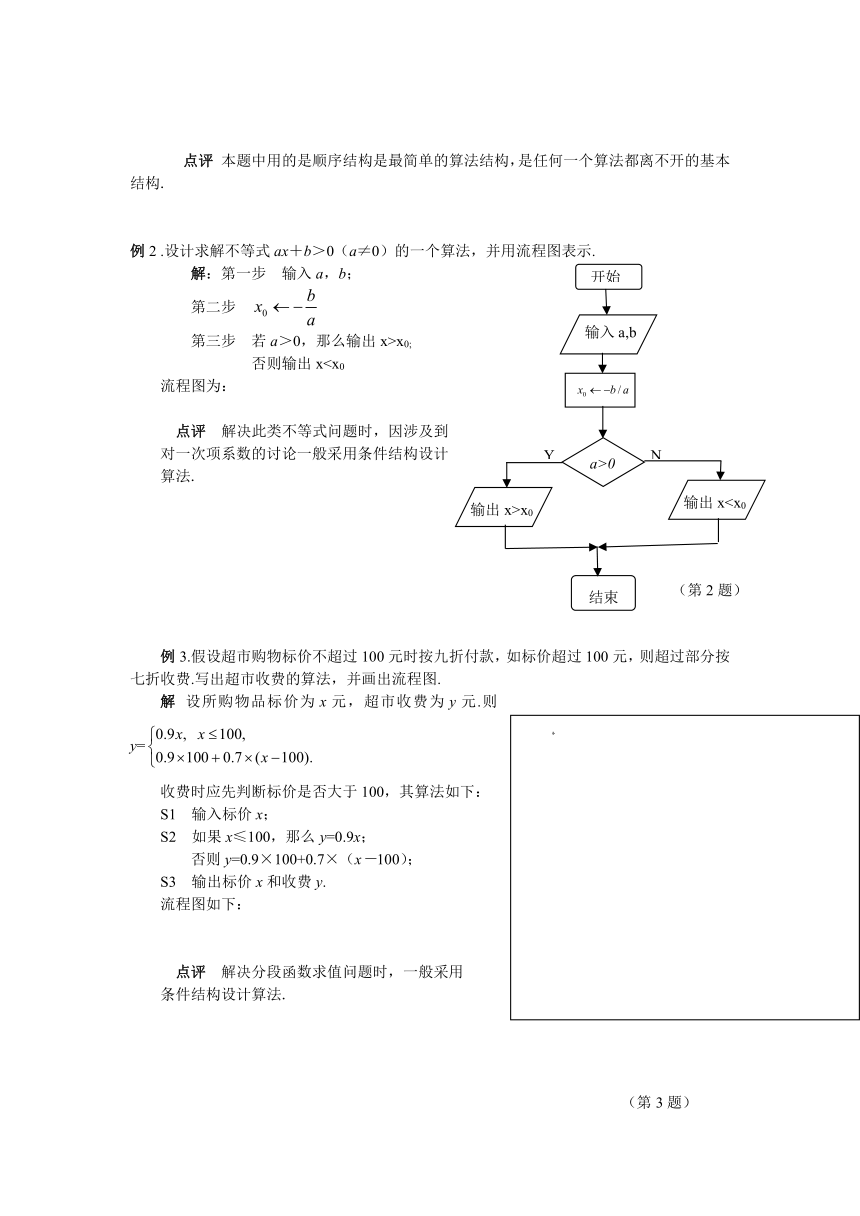
3.根据题意,完成流程图填空:
这是一个输入两个数,输出这两个数差的绝对值的一个算法.
请将空格部分填上适当的内容
(1) a>b ;(2) b-a
4.已知两个单元分别存放了变量x和y的值 ,试交换这两个变量值.
解 算法如下
S1 p←x;
S2 x←y;
S3 y←p.
【范例解析】
例1.已知梯形的上底、下底和高分别为5、8、9,写出求梯形的面积的算法,画出流程图.
解 算法如下
S1 a←5;
S2 b←8;
S3 h←9;
S4 S←(a+b)×h/2;
S5 输出S.
流程图为 :
点评 本题中用的是顺序结构是最简单的算法结构,是任何一个算法都离不开的基本结构.
例2 .设计求解不等式ax+b>0(a≠0)的一个算法,并用流程图表示.
解:第一步 输入a,b;
第二步
第三步 若a>0,那么输出x>x0;
否则输出x流程图为:
点评 解决此类不等式问题时,因涉及到
对一次项系数的讨论一般采用条件结构设计
算法.
例3.假设超市购物标价不超过100元时按九折付款,如标价超过100元,则超过部分按七折收费.写出超市收费的算法,并画出流程图.
解 设所购物品标价为x元,超市收费为y元.则 y=
收费时应先判断标价是否大于100,其算法如下:
S1 输入标价x;
S2 如果x≤100,那么y=0.9x;
否则y=0.9×100+0.7×(x-100);
S3 输出标价x和收费y.
流程图如下:
点评 解决分段函数求值问题时,一般采用
条件结构设计算法.
【反馈演练】
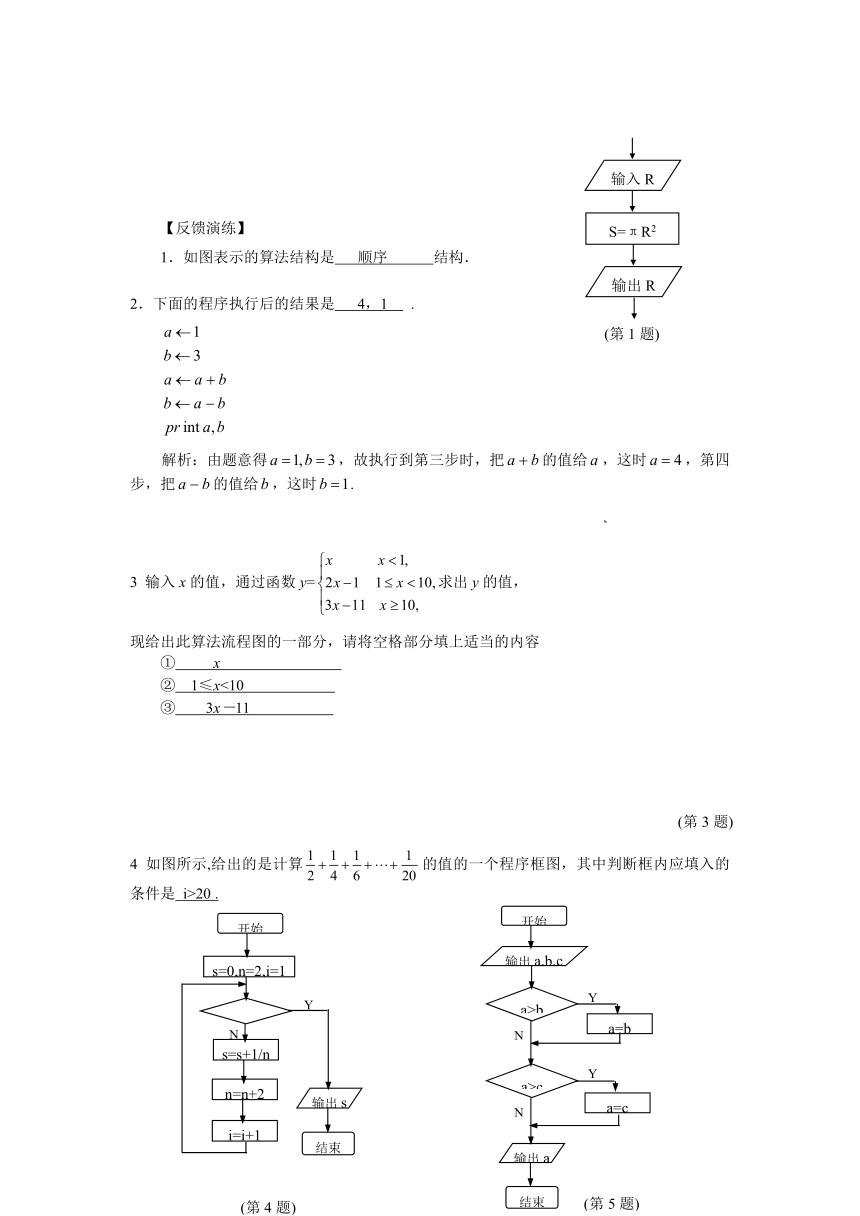
1.如图表示的算法结构是 顺序 结构.
2.下面的程序执行后的结果是 4,1 .
解析:由题意得,故执行到第三步时,把的值给,这时,第四步,把的值给,这时.
3 输入x的值,通过函数y=求出y的值,
现给出此算法流程图的一部分,请将空格部分填上适当的内容
① x
② 1≤x<10
③ 3x-11
4 如图所示,给出的是计算的值的一个程序框图,其中判断框内应填入的条件是 i>20 .
5. 给出以下一个算法的程序框图(如图所示).该程序框图的功能是 求出a,b,c三数中的最小数 .
6.根据下面的算法画出相应的流程图.
算法:
S1 T←0;
S2 I←2;
S3 T←T+I;
S4 I←I+2;
S5 如果I不大于200,转S3;
S6 输出T .
答案:解:这是计算2+4+6+…+200的一个算法.
流程图如下:
7.某学生五门功课成绩为80,95,78,87,65.写出求平均成绩的算法,画出流程图.
答案:解:算法如下:
S1 S←80;
S2 S←S+95;
S3 S←S+78;
S4 S←S+87;
S5 S←S+65;
S6 A←S/5;
S7 输出A.
流程图如下:
8.写出求1×3×5×7×9×11的算法,并画出流程图.
答案:解:算法如下:
S1 p←1;
S2 I←3;
S3 p←p×I;
S4 I←I+2;
S5 若I≤11,返回S3;否则,输出p值,结束.
9.《中华人民共和国个人所得税法》规定,公民全月工资、薪金所得不超过800元的
部分不必纳税,超过800元的部分为全月应纳税所得额,此项税款按下表分段累进计算:
全月应纳税所得额 税 率
不超过500元的部分 5%
超过500元至2000元的部分 10%
超过2000元至5000元的部分 15%
试写出工资x(x≤5000元)与税收y的函数关系式,给出计算应纳税所得额的算法及流程图.
答案:解:研究这个表提供的信息,可以发现,如果以一个人的工资、薪金所得为自变量x,那么应纳税款y=f(x)就是x的一个分段函数.
y=
算法为:
S1 输入工资x(x≤5000);
S2 如果x≤800,那么y=0;
如果800<x≤1300,那么y=0.05(x-800);
如果1300<x≤2800;
那么y=25+0.1(x-1300);
否则y=175+15%(x-2800);
S3 输出税收y,结束.
流程图如下:
(第3题)
开始
①
输入a,b
结束
输出a-b
输出 ②
N
Y
(第1题)
(第2题)
开始
a>0
输入a,b
结束
输出x>x0
输出xN
Y
(第3题)
输入R
S=πR2
输出R
(第1题)
(第3题)
(第5题)
结束
输出a
开始
a=b
输出a,b,c
a>b
a>c
a=c
Y
Y
N
N
结束
输出s
开始
s=0,n=2,i=1
s=s+1/n
n=n+2
i=i+1
Y
N
(第4题)
(第6题)
(第8题)
(第7题)
【考点导读】
了解常用流程图符号的意义,能用流程图表示顺序,选择,循环这三种基本结构,并能识别简单的流程图所描述的算法.高考要求对流程图有最基本的认识,并能解决相关的简单问题.
【基础练习】
1.算法的三种基本结构是 顺序结构、选择结构、循环结构 .
2.流程图中表示判断框的是 菱形框 .
3.根据题意,完成流程图填空:
这是一个输入两个数,输出这两个数差的绝对值的一个算法.
请将空格部分填上适当的内容
(1) a>b ;(2) b-a
4.已知两个单元分别存放了变量x和y的值 ,试交换这两个变量值.
解 算法如下
S1 p←x;
S2 x←y;
S3 y←p.
【范例解析】
例1.已知梯形的上底、下底和高分别为5、8、9,写出求梯形的面积的算法,画出流程图.
解 算法如下
S1 a←5;
S2 b←8;
S3 h←9;
S4 S←(a+b)×h/2;
S5 输出S.
流程图为 :
点评 本题中用的是顺序结构是最简单的算法结构,是任何一个算法都离不开的基本结构.
例2 .设计求解不等式ax+b>0(a≠0)的一个算法,并用流程图表示.
解:第一步 输入a,b;
第二步
第三步 若a>0,那么输出x>x0;
否则输出x
点评 解决此类不等式问题时,因涉及到
对一次项系数的讨论一般采用条件结构设计
算法.
例3.假设超市购物标价不超过100元时按九折付款,如标价超过100元,则超过部分按七折收费.写出超市收费的算法,并画出流程图.
解 设所购物品标价为x元,超市收费为y元.则 y=
收费时应先判断标价是否大于100,其算法如下:
S1 输入标价x;
S2 如果x≤100,那么y=0.9x;
否则y=0.9×100+0.7×(x-100);
S3 输出标价x和收费y.
流程图如下:
点评 解决分段函数求值问题时,一般采用
条件结构设计算法.
【反馈演练】
1.如图表示的算法结构是 顺序 结构.
2.下面的程序执行后的结果是 4,1 .
解析:由题意得,故执行到第三步时,把的值给,这时,第四步,把的值给,这时.
3 输入x的值,通过函数y=求出y的值,
现给出此算法流程图的一部分,请将空格部分填上适当的内容
① x
② 1≤x<10
③ 3x-11
4 如图所示,给出的是计算的值的一个程序框图,其中判断框内应填入的条件是 i>20 .
5. 给出以下一个算法的程序框图(如图所示).该程序框图的功能是 求出a,b,c三数中的最小数 .
6.根据下面的算法画出相应的流程图.
算法:
S1 T←0;
S2 I←2;
S3 T←T+I;
S4 I←I+2;
S5 如果I不大于200,转S3;
S6 输出T .
答案:解:这是计算2+4+6+…+200的一个算法.
流程图如下:
7.某学生五门功课成绩为80,95,78,87,65.写出求平均成绩的算法,画出流程图.
答案:解:算法如下:
S1 S←80;
S2 S←S+95;
S3 S←S+78;
S4 S←S+87;
S5 S←S+65;
S6 A←S/5;
S7 输出A.
流程图如下:
8.写出求1×3×5×7×9×11的算法,并画出流程图.
答案:解:算法如下:
S1 p←1;
S2 I←3;
S3 p←p×I;
S4 I←I+2;
S5 若I≤11,返回S3;否则,输出p值,结束.
9.《中华人民共和国个人所得税法》规定,公民全月工资、薪金所得不超过800元的
部分不必纳税,超过800元的部分为全月应纳税所得额,此项税款按下表分段累进计算:
全月应纳税所得额 税 率
不超过500元的部分 5%
超过500元至2000元的部分 10%
超过2000元至5000元的部分 15%
试写出工资x(x≤5000元)与税收y的函数关系式,给出计算应纳税所得额的算法及流程图.
答案:解:研究这个表提供的信息,可以发现,如果以一个人的工资、薪金所得为自变量x,那么应纳税款y=f(x)就是x的一个分段函数.
y=
算法为:
S1 输入工资x(x≤5000);
S2 如果x≤800,那么y=0;
如果800<x≤1300,那么y=0.05(x-800);
如果1300<x≤2800;
那么y=25+0.1(x-1300);
否则y=175+15%(x-2800);
S3 输出税收y,结束.
流程图如下:
(第3题)
开始
①
输入a,b
结束
输出a-b
输出 ②
N
Y
(第1题)
(第2题)
开始
a>0
输入a,b
结束
输出x>x0
输出x
Y
(第3题)
输入R
S=πR2
输出R
(第1题)
(第3题)
(第5题)
结束
输出a
开始
a=b
输出a,b,c
a>b
a>c
a=c
Y
Y
N
N
结束
输出s
开始
s=0,n=2,i=1
s=s+1/n
n=n+2
i=i+1
Y
N
(第4题)
(第6题)
(第8题)
(第7题)
同课章节目录
