考前最后一轮基础知识巩固之第十二章 第2课 导数的应用(1)
文档属性
| 名称 | 考前最后一轮基础知识巩固之第十二章 第2课 导数的应用(1) |  | |
| 格式 | zip | ||
| 文件大小 | 157.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | |||
| 科目 | 数学 | ||
| 更新时间 | 2012-06-04 15:34:31 | ||
图片预览


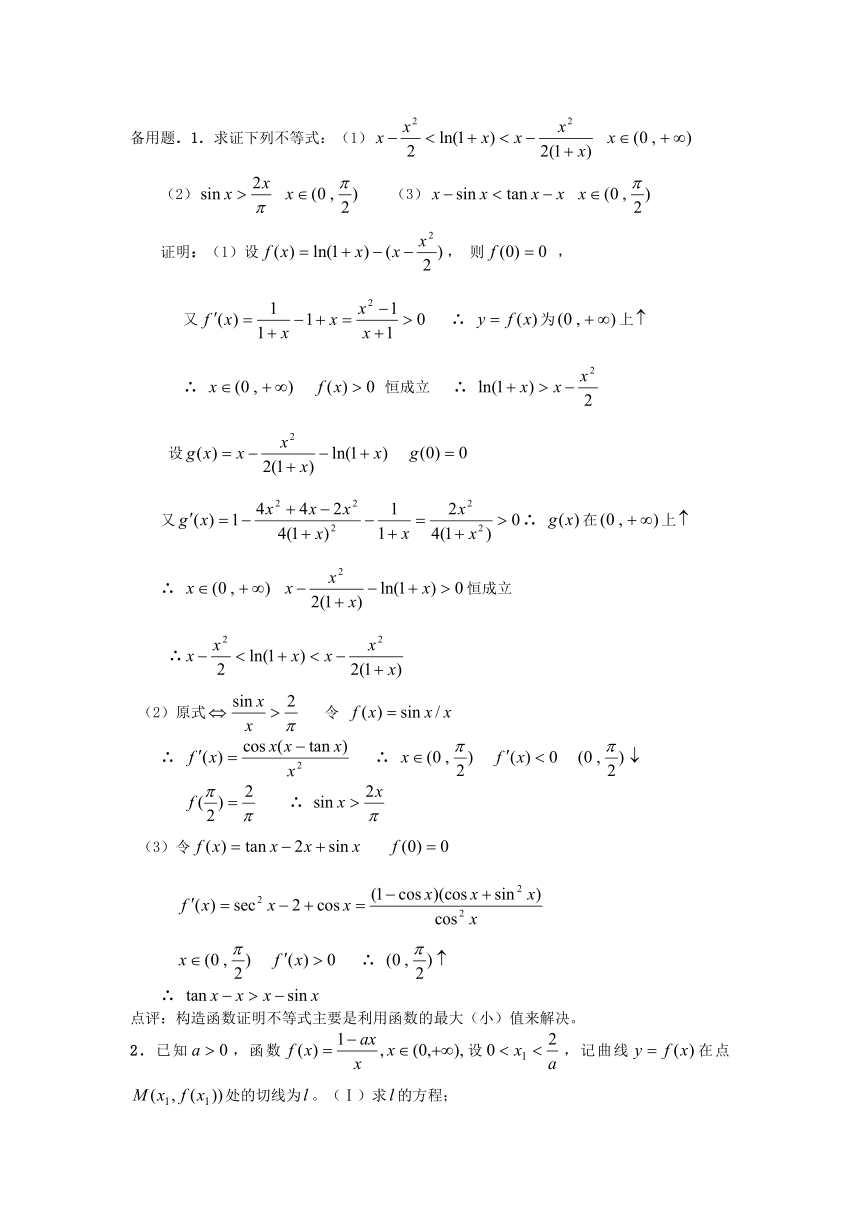
文档简介
第2课 导数的应用(1)
【考点导读】
通过数形结合的方法直观了解函数的单调性与导数的关系,能熟练利用导数研究函数的单调性;会求某些简单函数的单调区间。
结合函数的图象,了解函数的极大(小)值、最大(小)值与导数的关系;会求简单多项式函数的极大(小)值,以及在指定区间上的最大(小)值。
【基础练习】
1.若函数是上的单调函数,则应满足的条件是 。
2.函数在[0,3]上的最大值、最小值分别是 5,-15 。
3.用导数确定函数的单调减区间是。
4.函数的最大值是,最小值是。
5.函数的单调递增区间是 (-∞,-2)与(0,+ ∞) 。
【范例导析】
例1.(1)对于R上可导的任意函数f(x),若满足(x-1)0,比较f(0)+f(2)与2f(1)的大小: f(0)+f(2) 2f(1) 。
(2)在区间上的最大值是 2 。
解:(1)由题意得:当x1时,f(x)0,所以函数f(x)在(1,+)上是增函数;
当x1时,f(x)0,所以f(x)在(-,1)上是减函数,
故f(x)当x=1时取得最小值,即有f(0)f(1),f(2)f(1);
(2)当-1x0时,0,当0x1时,0,
所以当x=0时,f(x)取得最大值为2。
点评:用导数求极值或最值时要掌握一般方法,导数为0的点是否是极值点还取决与该点两侧的单调性,导数为0的点未必都是极值点,如:函数。
例2. 求下列函数单调区间:
(1) (2)
(3) (4)
解:(1)∵ ∴时
∴ ,
(2) ∴ ,
(3) ∴ ,
∴ , ,
(4) 定义域为
点评:熟练掌握单调性的求法,函数的单调性是解决函数的极值、最值问题的基础。
例3.设函数f(x)= (Ⅰ)求f(x)的单调区间;(Ⅱ)讨论f(x)的极值。
解:由已知得,令,解得 。
(Ⅰ)当时,,在上单调递增;
当时,,随的变化情况如下表:
0
+ 0 0
极大值 极小值
从上表可知,函数在上单调递增;在上单调递减;在上单调递增。
(Ⅱ)由(Ⅰ)知,当时,函数没有极值;
当时,函数在处取得极大值,在处取得极小值。
点评:本小题主要考查利用导数研究函数的最大值和最小值的基础知识,以及运用数学知识解决实际问题的能力。
备用题.1.求证下列不等式:(1)
(2) (3)
证明:(1)设, 则 ,
又 ∴ 为上
∴ 恒成立 ∴
设
又∴ 在上
∴ 恒成立
∴
(2)原式 令
∴ ∴
∴
(3)令
∴
∴
点评:构造函数证明不等式主要是利用函数的最大(小)值来解决。
2.已知,函数设,记曲线在点处的切线为。(Ⅰ)求的方程;
(Ⅱ)设与轴的交点为,证明:①②若,则
解:(1)的导数,由此得切线的方程:,
(2)依题得,切线方程中令,得
,其中,
(ⅰ)由,,有,及,
∴,当且仅当时,。
(ⅱ)当时,,因此,,且由(ⅰ),,
所以。
【反馈演练】
1.关于函数,下列说法不正确的是 (4) 。
(1)在区间(,0)内,为增函数 (2)在区间(0,2)内,为减函数
(3)在区间(2,)内,为增函数 (4)在区间(,0)内,为增函数
2.对任意x,有,,则此函数为 。
3.函数y=2x3-3x2-12x+5在[0,3]上的最大值与最小值分别是 5 , -15 。
4. f()是定义在区间[-c,c]上的奇函数,其图象如图所示:令,则下
列关于函数g()的叙述正确的是 (2) 。
(1)若a<0,则函数g()的图象关于原点对称.
(2)若a=-1,-2(3)若a≠0,b=2,则方程g()=0有两个实根.
(4)若a≥1,b<2,则方程g()=0有三个实根.
5.下列函数中,是极值点的函数是 (2) 。
(1) (2) (3) (4)
6.下列说法正确的是 (4) 。
(1)函数的极大值就是函数的最大值 (2)函数的极小值就是函数的最小值
(3)函数的最值一定是极值 (4)在闭区间上的连续函数一定存在最值
7.函数的单调减区间是 [0,2] 。
8.若函数在内是减函数,在内是增函数,则 2 。
9.函数的极大值是,极小值是。
10.求证:方程在区间内有且仅有一个实根。
分析:本题直接求方程的根是不可能的,从图象上可以进行判断,但是图象用在证明中是不妥当的,我们可以借助函数的单调性来解决这个问题。
证明:令, 则
当时,, 所以在
又
∴ 在内与轴有且仅有一个交点
∴ 方程 在内仅有一解
点评:本题通过判断函数的单调性来判断方程的零点的个数,这也是导数在函数中的灵活运用。
11.求满足条件的的范围:(1)使为上增函数;
(2)使为上的增函数;(3)使为上的增函数。
解:(1)∵ 由题意可知:对都成立 ∴
又当时 也符合条件 ∴
(2)同上
(3)同上
12.已知函数(x>0)在x = 1处取得极值,其中为常数。
(1)试确定的值;
(2)讨论函数f(x)的单调区间;
(3)若对任意x>0,不等式恒成立,求c的取值范围。
解:(I)由题意知,因此,从而.
又对求导得.
由题意,因此,解得.
(II)由(I)知(),令,解得.
当时,,此时为减函数;当时,,此时为增函数.
因此的单调递减区间为,而的单调递增区间为.
(III)由(II)知,在处取得极小值,此极小值也是最小值,
要使()恒成立,只需.
即,从而,
解得或.
所以的取值范围为.
【考点导读】
通过数形结合的方法直观了解函数的单调性与导数的关系,能熟练利用导数研究函数的单调性;会求某些简单函数的单调区间。
结合函数的图象,了解函数的极大(小)值、最大(小)值与导数的关系;会求简单多项式函数的极大(小)值,以及在指定区间上的最大(小)值。
【基础练习】
1.若函数是上的单调函数,则应满足的条件是 。
2.函数在[0,3]上的最大值、最小值分别是 5,-15 。
3.用导数确定函数的单调减区间是。
4.函数的最大值是,最小值是。
5.函数的单调递增区间是 (-∞,-2)与(0,+ ∞) 。
【范例导析】
例1.(1)对于R上可导的任意函数f(x),若满足(x-1)0,比较f(0)+f(2)与2f(1)的大小: f(0)+f(2) 2f(1) 。
(2)在区间上的最大值是 2 。
解:(1)由题意得:当x1时,f(x)0,所以函数f(x)在(1,+)上是增函数;
当x1时,f(x)0,所以f(x)在(-,1)上是减函数,
故f(x)当x=1时取得最小值,即有f(0)f(1),f(2)f(1);
(2)当-1x0时,0,当0x1时,0,
所以当x=0时,f(x)取得最大值为2。
点评:用导数求极值或最值时要掌握一般方法,导数为0的点是否是极值点还取决与该点两侧的单调性,导数为0的点未必都是极值点,如:函数。
例2. 求下列函数单调区间:
(1) (2)
(3) (4)
解:(1)∵ ∴时
∴ ,
(2) ∴ ,
(3) ∴ ,
∴ , ,
(4) 定义域为
点评:熟练掌握单调性的求法,函数的单调性是解决函数的极值、最值问题的基础。
例3.设函数f(x)= (Ⅰ)求f(x)的单调区间;(Ⅱ)讨论f(x)的极值。
解:由已知得,令,解得 。
(Ⅰ)当时,,在上单调递增;
当时,,随的变化情况如下表:
0
+ 0 0
极大值 极小值
从上表可知,函数在上单调递增;在上单调递减;在上单调递增。
(Ⅱ)由(Ⅰ)知,当时,函数没有极值;
当时,函数在处取得极大值,在处取得极小值。
点评:本小题主要考查利用导数研究函数的最大值和最小值的基础知识,以及运用数学知识解决实际问题的能力。
备用题.1.求证下列不等式:(1)
(2) (3)
证明:(1)设, 则 ,
又 ∴ 为上
∴ 恒成立 ∴
设
又∴ 在上
∴ 恒成立
∴
(2)原式 令
∴ ∴
∴
(3)令
∴
∴
点评:构造函数证明不等式主要是利用函数的最大(小)值来解决。
2.已知,函数设,记曲线在点处的切线为。(Ⅰ)求的方程;
(Ⅱ)设与轴的交点为,证明:①②若,则
解:(1)的导数,由此得切线的方程:,
(2)依题得,切线方程中令,得
,其中,
(ⅰ)由,,有,及,
∴,当且仅当时,。
(ⅱ)当时,,因此,,且由(ⅰ),,
所以。
【反馈演练】
1.关于函数,下列说法不正确的是 (4) 。
(1)在区间(,0)内,为增函数 (2)在区间(0,2)内,为减函数
(3)在区间(2,)内,为增函数 (4)在区间(,0)内,为增函数
2.对任意x,有,,则此函数为 。
3.函数y=2x3-3x2-12x+5在[0,3]上的最大值与最小值分别是 5 , -15 。
4. f()是定义在区间[-c,c]上的奇函数,其图象如图所示:令,则下
列关于函数g()的叙述正确的是 (2) 。
(1)若a<0,则函数g()的图象关于原点对称.
(2)若a=-1,-2
(4)若a≥1,b<2,则方程g()=0有三个实根.
5.下列函数中,是极值点的函数是 (2) 。
(1) (2) (3) (4)
6.下列说法正确的是 (4) 。
(1)函数的极大值就是函数的最大值 (2)函数的极小值就是函数的最小值
(3)函数的最值一定是极值 (4)在闭区间上的连续函数一定存在最值
7.函数的单调减区间是 [0,2] 。
8.若函数在内是减函数,在内是增函数,则 2 。
9.函数的极大值是,极小值是。
10.求证:方程在区间内有且仅有一个实根。
分析:本题直接求方程的根是不可能的,从图象上可以进行判断,但是图象用在证明中是不妥当的,我们可以借助函数的单调性来解决这个问题。
证明:令, 则
当时,, 所以在
又
∴ 在内与轴有且仅有一个交点
∴ 方程 在内仅有一解
点评:本题通过判断函数的单调性来判断方程的零点的个数,这也是导数在函数中的灵活运用。
11.求满足条件的的范围:(1)使为上增函数;
(2)使为上的增函数;(3)使为上的增函数。
解:(1)∵ 由题意可知:对都成立 ∴
又当时 也符合条件 ∴
(2)同上
(3)同上
12.已知函数(x>0)在x = 1处取得极值,其中为常数。
(1)试确定的值;
(2)讨论函数f(x)的单调区间;
(3)若对任意x>0,不等式恒成立,求c的取值范围。
解:(I)由题意知,因此,从而.
又对求导得.
由题意,因此,解得.
(II)由(I)知(),令,解得.
当时,,此时为减函数;当时,,此时为增函数.
因此的单调递减区间为,而的单调递增区间为.
(III)由(II)知,在处取得极小值,此极小值也是最小值,
要使()恒成立,只需.
即,从而,
解得或.
所以的取值范围为.
同课章节目录
