2020-2021学年安徽省高一(上)数学期末试卷人教新课标A版(Word含答案)
文档属性
| 名称 | 2020-2021学年安徽省高一(上)数学期末试卷人教新课标A版(Word含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 149.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-17 10:04:28 | ||
图片预览



文档简介
2020-2021学年安徽省高一(上)期末数学试卷
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
?
1.
已知全集=,=,,则等于(
)
A.
B.
C.
D.
?
2.
已知命题,,则¬是(
)
A.,
B.,
C.,
D.,
?
3.
已知,则的取值范围是(
)
A.
B.
C.
D.
?
4.
已知,则(
)
A.
B.
C.
D.
?
5.
集合=,=,则(
)
A.=
B.=
C.
D.
?
6.
函数的最小值为(
)
A.
B.
C.
D.
?
7.
关于函数.下列说法错误的是(
)
A.的图象关于轴对称
B.在上单调递增,在上单调递减
C.的值域为
D.不等式的解集为
?
8.
某银行出售种不同款式的纪念币,甲、乙、丙三人都各自收集这些纪念币.下列说法正确的(
)
A.若甲、乙、丙三人各自收集款纪念币,则至少有款纪念币是三人都拥有
B.若甲、乙、丙三人各自收集款纪念币,则至少有款纪念币是三人都拥有
C.若甲、乙两人各自收集款纪念币,则至少有款纪念币是两人都拥有
D.若甲、乙两人各自收集款纪念币,则他们两人合起来一定会收集到这款不同的纪念币
?
9.
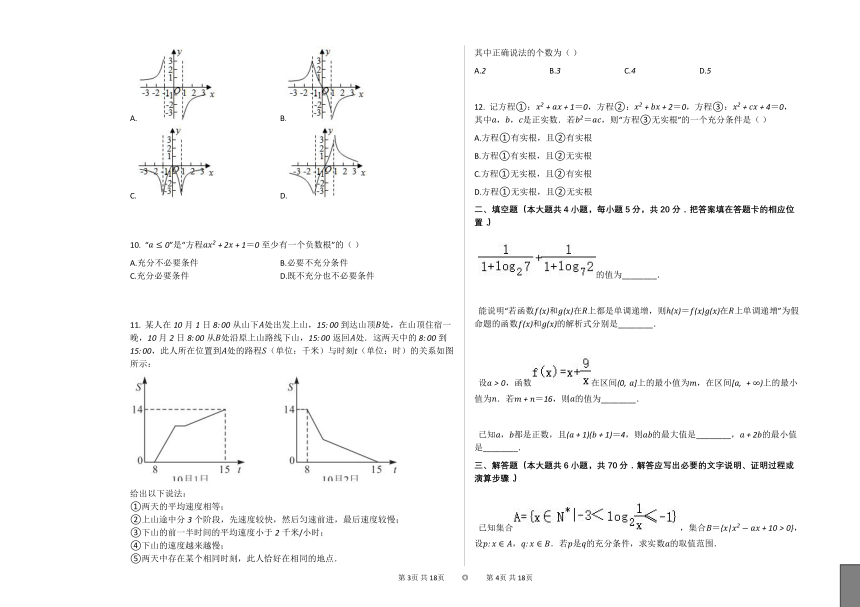
函数的大致图象是(
)
A.
B.
C.
D.
?
10.
“”是“方程=至少有一个负数根”的(
)
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件
?
11.
某人在月日从山下处出发上山,到达山顶处,在山顶住宿一晚,月日从处沿原上山路线下山,返回处.这两天中的到,此人所在位置到处的路程(单位:千米)与时刻(单位:时)的关系如图所示:
给出以下说法:
①两天的平均速度相等;
②上山途中分个阶段,先速度较快,然后匀速前进,最后速度较慢;
③下山的前一半时间的平均速度小于千米/小时;
④下山的速度越来越慢;
⑤两天中存在某个相同时刻,此人恰好在相同的地点.
其中正确说法的个数为(
)
A.
B.
C.
D.
?
12.
记方程①:=,方程②:=,方程③:=,其中,,是正实数.若=,则“方程③无实根”的一个充分条件是(
)
A.方程①有实根,且②有实根
B.方程①有实根,且②无实根
C.方程①无实根,且②有实根
D.方程①无实根,且②无实根
二、填空题(本大题共4小题,每小题5分,共20分.把答案填在答题卡的相应位置.)
?
的值为________.
?
能说明“若函数和在上都是单调递增,则=在上单调递增”为假命题的函数和的解析式分别是________.
?
设,函数在区间上的最小值为,在区间上的最小值为.若=,则的值为________.
?
已知,都是正数,且=,则的最大值是________,的最小值是________.
三、解答题(本大题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤.)
?
已知集合,集合=,设,.若是的充分条件,求实数的取值范围.
?
已知函数=.
(1)求不等式的解集;
(2)若的最小值为,正数,满足=,求的最小值.
?
已知函数=.
(1)若,求的取值范围;
(2)求函数在的最小值.
?
已知奇函数.
(1)当为何值时,函数为奇函数?并证明你的结论;
(2)判断并证明函数的单调性;
(3)若=,解不等式:.
?
设,函数.
(1)当时,求证:;
(2)若=恰有三个不同的零点,且是其中的一个零点,求实数的值.
?
随着我国人民生活水平的提高,家用汽车的数量逐渐增加,同时交通拥挤现象也越来越严重,对上班族的通勤时间有较大影响.某群体的人均通勤时间,是指该群体中成员从居住地到工作地的单趟平均用时,假设某城市上班族中的成员仅以自驾或公交方式通勤,采用公交方式通勤的群体(公交群体)的人均通勤时间为分钟,采用自驾方式通勤的群体(自驾群体)的人均通勤时间(单位:分钟)与自驾群体在中的百分数的关系为:.
(1)上班族成员小李按群体人均通勤时间为决策依据,决定采用自驾通勤方式,求的取值范围(若群体人均通勤时间相等,则采用公交通勤方式).
(2)求该城市上班族的人均通勤时间(单位:分钟),并求的最小值.
参考答案与试题解析
2020-2021学年安徽省示范高中培优联盟高一(上)冬季联赛数学试卷
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.
【答案】
D
【考点】
交、并、补集的混合运算
【解析】
此题暂无解析
【解答】
此题暂无解答
2.
【答案】
D
【考点】
命题的否定
【解析】
此题暂无解析
【解答】
此题暂无解答
3.
【答案】
C
【考点】
不等式的基本性质
【解析】
此题暂无解析
【解答】
此题暂无解答
4.
【答案】
B
【考点】
对数值大小的比较
【解析】
此题暂无解析
【解答】
此题暂无解答
5.
【答案】
D
【考点】
集合的包含关系判断及应用
交集及其运算
【解析】
此题暂无解析
【解答】
此题暂无解答
6.
【答案】
C
【考点】
基本不等式及其应用
【解析】
此题暂无解析
【解答】
此题暂无解答
7.
【答案】
D
【考点】
函数的值域及其求法
命题的真假判断与应用
【解析】
此题暂无解析
【解答】
此题暂无解答
8.
【答案】
C
【考点】
进行简单的合情推理
【解析】
此题暂无解析
【解答】
此题暂无解答
9.
【答案】
D
【考点】
函数的图象变换
【解析】
根据函数的奇偶性和函数值的特点即可判断
【解答】
解∵
,
∴
,
∴
为奇函数,排除
当,则,故排除,
当时,,故排除
10.
【答案】
C
【考点】
充分条件、必要条件、充要条件
【解析】
此题暂无解析
【解答】
此题暂无解答
11.
【答案】
A
【考点】
函数的图象与图象的变换
【解析】
此题暂无解析
【解答】
此题暂无解答
12.
【答案】
B
【考点】
充分条件、必要条件、充要条件
【解析】
此题暂无解析
【解答】
此题暂无解答
二、填空题(本大题共4小题,每小题5分,共20分.把答案填在答题卡的相应位置.)
【答案】
【考点】
对数的运算性质
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
=和=,答案不唯一.
【考点】
函数单调性的性质与判断
函数解析式的求解及常用方法
函数的单调性及单调区间
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
或
【考点】
函数的最值及其几何意义
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
,
【考点】
基本不等式及其应用
【解析】
此题暂无解析
【解答】
此题暂无解答
三、解答题(本大题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤.)
【答案】
由,得,
即=,
因为是的充分条件,
所以,
转化为不等式是在=上恒成立,
进一步可得对于,,,,,
在上的最小值为=时的函数值,
所以.故实数的取值范围是.
【考点】
充分条件、必要条件、充要条件
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
函数=.
若,则有或,
解得或,
即.
故原不等式的解集为;
函数,
当时,,即=.
正数,满足=,∴
,
令,当且仅当==时取最小值为.
又∵
在区间,
∴
在=时取得最小值,
故的最小值为(此时==).
【考点】
基本不等式及其应用
绝对值不等式的解法与证明
函数的最值及其几何意义
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
,
因为(当且仅当时,
所以,所以,得.
记函数在的最小值,
则函数变为=,
因为=在时单调递减,在时单调递增,
所以①当,即时,=在单调递增,
所以==;
②当,即时,==;
③当,即时在单调递减,
所以==;
综上,.
【考点】
函数最值的应用
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
当时,函数为奇函数
易知函数的定义域为,且
,
=,
所以,函数为奇函数.
在上任取,,且,因为,所以,
又因为,,
所以,
,,
故,
即,
所以,所以,
所以,函数函数在上单调递增.
由(1)(2)可知,=为偶函数,
且在单调递减,单调递增,
又==,
所以的解集为.
【考点】
函数奇偶性的性质与判断
奇偶性与单调性的综合
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
当时,,
所以,
当时,,进而可得,
即;
由于函数是偶函数,
故方程=的三个实数解关于数轴原点对称分布,从而必有.
由(1)可知,当时,,
当时,在上单调递增,
且当时,
当时,在上单调递减,
且当时,
又因为是其中的一个零点,所以,所以.
【考点】
函数的零点与方程根的关系
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
当时,自驾群体的人均通勤时间为分钟,此时小李采用自驾通勤方式,
当时,因为小李采用自驾通勤方式,
即,
解得,所以,
综上,,
即的取值范围为,).
设上班族中有人,则自驾群体中有人,
当时,,
当时,,
所以,
当时,=,
当时,,
因为,
所以,当时,的最小值为(分钟).
【考点】
根据实际问题选择函数类型
【解析】
此题暂无解析
【解答】
此题暂无解答
第7页
共20页
◎
第8页
共20页
第9页
共20页
◎
第10页
共20页
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
?
1.
已知全集=,=,,则等于(
)
A.
B.
C.
D.
?
2.
已知命题,,则¬是(
)
A.,
B.,
C.,
D.,
?
3.
已知,则的取值范围是(
)
A.
B.
C.
D.
?
4.
已知,则(
)
A.
B.
C.
D.
?
5.
集合=,=,则(
)
A.=
B.=
C.
D.
?
6.
函数的最小值为(
)
A.
B.
C.
D.
?
7.
关于函数.下列说法错误的是(
)
A.的图象关于轴对称
B.在上单调递增,在上单调递减
C.的值域为
D.不等式的解集为
?
8.
某银行出售种不同款式的纪念币,甲、乙、丙三人都各自收集这些纪念币.下列说法正确的(
)
A.若甲、乙、丙三人各自收集款纪念币,则至少有款纪念币是三人都拥有
B.若甲、乙、丙三人各自收集款纪念币,则至少有款纪念币是三人都拥有
C.若甲、乙两人各自收集款纪念币,则至少有款纪念币是两人都拥有
D.若甲、乙两人各自收集款纪念币,则他们两人合起来一定会收集到这款不同的纪念币
?
9.
函数的大致图象是(
)
A.
B.
C.
D.
?
10.
“”是“方程=至少有一个负数根”的(
)
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件
?
11.
某人在月日从山下处出发上山,到达山顶处,在山顶住宿一晚,月日从处沿原上山路线下山,返回处.这两天中的到,此人所在位置到处的路程(单位:千米)与时刻(单位:时)的关系如图所示:
给出以下说法:
①两天的平均速度相等;
②上山途中分个阶段,先速度较快,然后匀速前进,最后速度较慢;
③下山的前一半时间的平均速度小于千米/小时;
④下山的速度越来越慢;
⑤两天中存在某个相同时刻,此人恰好在相同的地点.
其中正确说法的个数为(
)
A.
B.
C.
D.
?
12.
记方程①:=,方程②:=,方程③:=,其中,,是正实数.若=,则“方程③无实根”的一个充分条件是(
)
A.方程①有实根,且②有实根
B.方程①有实根,且②无实根
C.方程①无实根,且②有实根
D.方程①无实根,且②无实根
二、填空题(本大题共4小题,每小题5分,共20分.把答案填在答题卡的相应位置.)
?
的值为________.
?
能说明“若函数和在上都是单调递增,则=在上单调递增”为假命题的函数和的解析式分别是________.
?
设,函数在区间上的最小值为,在区间上的最小值为.若=,则的值为________.
?
已知,都是正数,且=,则的最大值是________,的最小值是________.
三、解答题(本大题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤.)
?
已知集合,集合=,设,.若是的充分条件,求实数的取值范围.
?
已知函数=.
(1)求不等式的解集;
(2)若的最小值为,正数,满足=,求的最小值.
?
已知函数=.
(1)若,求的取值范围;
(2)求函数在的最小值.
?
已知奇函数.
(1)当为何值时,函数为奇函数?并证明你的结论;
(2)判断并证明函数的单调性;
(3)若=,解不等式:.
?
设,函数.
(1)当时,求证:;
(2)若=恰有三个不同的零点,且是其中的一个零点,求实数的值.
?
随着我国人民生活水平的提高,家用汽车的数量逐渐增加,同时交通拥挤现象也越来越严重,对上班族的通勤时间有较大影响.某群体的人均通勤时间,是指该群体中成员从居住地到工作地的单趟平均用时,假设某城市上班族中的成员仅以自驾或公交方式通勤,采用公交方式通勤的群体(公交群体)的人均通勤时间为分钟,采用自驾方式通勤的群体(自驾群体)的人均通勤时间(单位:分钟)与自驾群体在中的百分数的关系为:.
(1)上班族成员小李按群体人均通勤时间为决策依据,决定采用自驾通勤方式,求的取值范围(若群体人均通勤时间相等,则采用公交通勤方式).
(2)求该城市上班族的人均通勤时间(单位:分钟),并求的最小值.
参考答案与试题解析
2020-2021学年安徽省示范高中培优联盟高一(上)冬季联赛数学试卷
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.
【答案】
D
【考点】
交、并、补集的混合运算
【解析】
此题暂无解析
【解答】
此题暂无解答
2.
【答案】
D
【考点】
命题的否定
【解析】
此题暂无解析
【解答】
此题暂无解答
3.
【答案】
C
【考点】
不等式的基本性质
【解析】
此题暂无解析
【解答】
此题暂无解答
4.
【答案】
B
【考点】
对数值大小的比较
【解析】
此题暂无解析
【解答】
此题暂无解答
5.
【答案】
D
【考点】
集合的包含关系判断及应用
交集及其运算
【解析】
此题暂无解析
【解答】
此题暂无解答
6.
【答案】
C
【考点】
基本不等式及其应用
【解析】
此题暂无解析
【解答】
此题暂无解答
7.
【答案】
D
【考点】
函数的值域及其求法
命题的真假判断与应用
【解析】
此题暂无解析
【解答】
此题暂无解答
8.
【答案】
C
【考点】
进行简单的合情推理
【解析】
此题暂无解析
【解答】
此题暂无解答
9.
【答案】
D
【考点】
函数的图象变换
【解析】
根据函数的奇偶性和函数值的特点即可判断
【解答】
解∵
,
∴
,
∴
为奇函数,排除
当,则,故排除,
当时,,故排除
10.
【答案】
C
【考点】
充分条件、必要条件、充要条件
【解析】
此题暂无解析
【解答】
此题暂无解答
11.
【答案】
A
【考点】
函数的图象与图象的变换
【解析】
此题暂无解析
【解答】
此题暂无解答
12.
【答案】
B
【考点】
充分条件、必要条件、充要条件
【解析】
此题暂无解析
【解答】
此题暂无解答
二、填空题(本大题共4小题,每小题5分,共20分.把答案填在答题卡的相应位置.)
【答案】
【考点】
对数的运算性质
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
=和=,答案不唯一.
【考点】
函数单调性的性质与判断
函数解析式的求解及常用方法
函数的单调性及单调区间
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
或
【考点】
函数的最值及其几何意义
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
,
【考点】
基本不等式及其应用
【解析】
此题暂无解析
【解答】
此题暂无解答
三、解答题(本大题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤.)
【答案】
由,得,
即=,
因为是的充分条件,
所以,
转化为不等式是在=上恒成立,
进一步可得对于,,,,,
在上的最小值为=时的函数值,
所以.故实数的取值范围是.
【考点】
充分条件、必要条件、充要条件
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
函数=.
若,则有或,
解得或,
即.
故原不等式的解集为;
函数,
当时,,即=.
正数,满足=,∴
,
令,当且仅当==时取最小值为.
又∵
在区间,
∴
在=时取得最小值,
故的最小值为(此时==).
【考点】
基本不等式及其应用
绝对值不等式的解法与证明
函数的最值及其几何意义
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
,
因为(当且仅当时,
所以,所以,得.
记函数在的最小值,
则函数变为=,
因为=在时单调递减,在时单调递增,
所以①当,即时,=在单调递增,
所以==;
②当,即时,==;
③当,即时在单调递减,
所以==;
综上,.
【考点】
函数最值的应用
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
当时,函数为奇函数
易知函数的定义域为,且
,
=,
所以,函数为奇函数.
在上任取,,且,因为,所以,
又因为,,
所以,
,,
故,
即,
所以,所以,
所以,函数函数在上单调递增.
由(1)(2)可知,=为偶函数,
且在单调递减,单调递增,
又==,
所以的解集为.
【考点】
函数奇偶性的性质与判断
奇偶性与单调性的综合
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
当时,,
所以,
当时,,进而可得,
即;
由于函数是偶函数,
故方程=的三个实数解关于数轴原点对称分布,从而必有.
由(1)可知,当时,,
当时,在上单调递增,
且当时,
当时,在上单调递减,
且当时,
又因为是其中的一个零点,所以,所以.
【考点】
函数的零点与方程根的关系
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
当时,自驾群体的人均通勤时间为分钟,此时小李采用自驾通勤方式,
当时,因为小李采用自驾通勤方式,
即,
解得,所以,
综上,,
即的取值范围为,).
设上班族中有人,则自驾群体中有人,
当时,,
当时,,
所以,
当时,=,
当时,,
因为,
所以,当时,的最小值为(分钟).
【考点】
根据实际问题选择函数类型
【解析】
此题暂无解析
【解答】
此题暂无解答
第7页
共20页
◎
第8页
共20页
第9页
共20页
◎
第10页
共20页
同课章节目录
