北师大数学五年级(上)第一单元《人民币兑换》第二节 课件
文档属性
| 名称 | 北师大数学五年级(上)第一单元《人民币兑换》第二节 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 834.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-17 00:00:00 | ||
图片预览







文档简介
人民币兑换
第一单元小数除法第二课时
课堂导入
课堂总结
课堂练习
新知探究
课堂作业
北师大版 数学 五年级 上册
学习目标
1.结合人民币兑换情境,探索除数大于(或小于1、接近1)时,商与被除数之间的关系。
2.能应用探索出的规律进行一些小数除法的估算与计算。
3.感受数学与生活的密切联系,体会学习数学的必要性,提高学习数学的积极性。
课堂导入
1.12.5美元可以兑换多少元人民币?(1美元兑换人民币6.31元)
12.5×6.31≈78.88(元)
答:可以兑换78.88元人民币。
运用的是“四舍五入”法
2.做一套童装需要2.2米布,30米布最多可以做多少套这样的童装?
30÷2.2≈13(套)
答:最多可以做13套这样的童装。
运用的是“去尾法”
3.妈妈要装10kg油需要几个这样的油桶?
10÷4.5≈3(个)
答:需要3个这样的油桶。
运用的是“进一法”
探究新知
学校科技小组去日本参加活动,老师到银行把5000元人民币兑换成日元,能兑换多少日元?
中国银行
2012年10月X日
1美元兑换人民币6.31元
1欧元兑换人民币8.19元
1港元兑换人民币0.81元
1新元兑换人民币5.11元
100日元兑换人民币7.89元
100泰铢兑换人民币20.32元
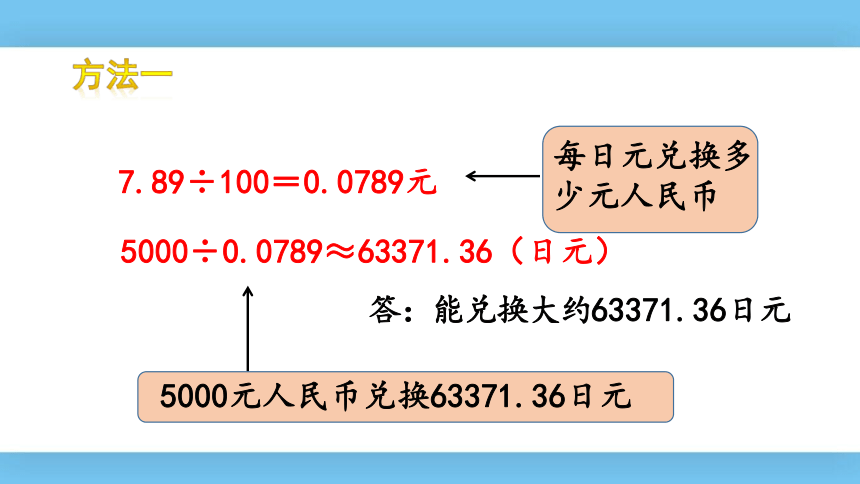
方法一
7.89÷100=0.0789元
5000÷0.0789≈63371.36(日元)
每日元兑换多少元人民币
5000元人民币兑换63371.36日元
答:能兑换大约63371.36日元
方法二
633.7136×100=63371.36日元
5000÷7.89≈633.7136(日元)
5000元人民币里有多少个7.89元
5000元人民币兑换63371.36日元
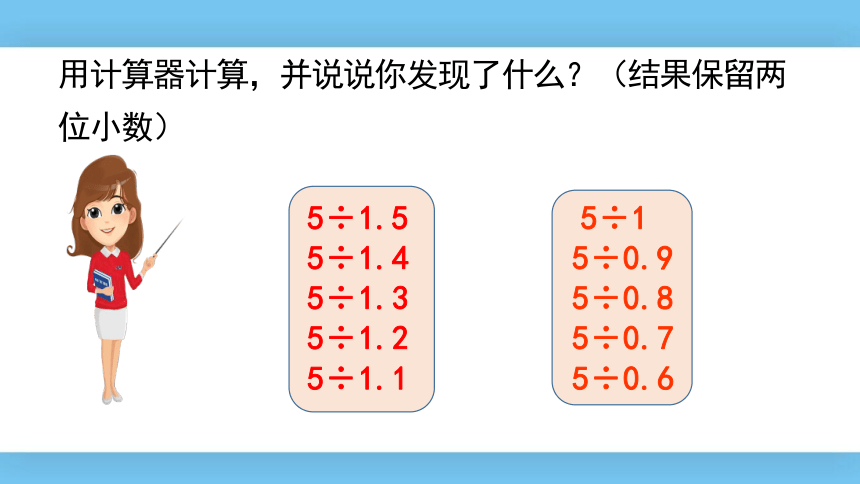
用计算器计算,并说说你发现了什么?(结果保留两位小数)
5÷1.5
5÷1.4
5÷1.3
5÷1.2
5÷1.1
5÷1
5÷0.9
5÷0.8
5÷0.7
5÷0.6
小组合作任务:
1.每组3号同学对答案,其他同学倾听、纠正。
2.组长组织组员依次分享自己的发现,其他组员质疑、补充。
3.整理大家的发现,记录员做好记录。
4.汇报员准备汇报。
≈3.33
≈3.57
≈3.85
≈4.17
≈4.55
=5
≈5.56
=6.25
≈7.14
≈8.33
除数大于1,商比被除数小。
除数小于1,商比被除数大。
除数越接近1,商越接近被除数。
用计算器计算,并说说你发现了什么?(结果保留两位小数)
5÷1.5
5÷1.4
5÷1.3
5÷1.2
5÷1.1
5÷1
5÷0.9
5÷0.8
5÷0.7
5÷0.6
发现
课堂练习
1.根据所学的规律,不计算,判断大小。
1.5÷1.1
<
1.5
3.5÷1
>
3.5
5.7÷1.2
<
5.7
1.25÷0.9
>
1.25
想一想,填一填。
算一算,你发现了什么?请你再写出一组类似的算式。
10÷0.8
10÷0.9
10÷1
10÷1.1
10÷1.2
10÷1.3
=12.5
≈11.11
=10
≈9.09
≈8.33
≈7.69
发现:当除数大于1时,商小于被除数;当除数小于
1时,商大于被除数;当除数接近1时,商也接
近被除数;当除数等于1时,商等于被除数。
想一想,算一算,你有什么发现?
12÷1.2
12÷1.2÷1.2
12÷1.2÷1.2÷1.2
=10
≈8.33
≈6.94
(1)
12÷0.8
12÷0.8÷0.8
12÷0.8÷0.8÷0.8
=15
=18.75
=23.4375
(2)
当除数大于1时,对同一个除数相除的次数越多,商越小;反之,商越大。
你能再写出一组类似算式说明你的发现吗?
课堂小结
当除数大于1时,商小于被除数;当除数小于1时,商大于被除数;当除数接近1时,商也接近被除数;当除数等于1时,商等于被除数.
课堂作业
1.按照1美元兑换6.31元人民币,美国籍教师安迪在中国工作,每月工资5000元,到银行能兑换多少美元?(保留两位小数)
5000÷6.31≈792.39(美元)
答:能兑换792.39美元。
2.想一想,算一算,通过这两组计算你有什么发现?
24÷1.2
24÷1.2÷1.2
24÷1.2÷1.2÷1.2
=20
≈16.67
≈13.89
(1)
24÷0.8
24÷0.8÷0.8
24÷0.8÷0.8÷0.8
=30
=37.5
=46.875
(2)
发现:当除数大于1时,对同一个除数相除的次数越多,商越小;反之,商越大。
第一单元小数除法第二课时
课堂导入
课堂总结
课堂练习
新知探究
课堂作业
北师大版 数学 五年级 上册
学习目标
1.结合人民币兑换情境,探索除数大于(或小于1、接近1)时,商与被除数之间的关系。
2.能应用探索出的规律进行一些小数除法的估算与计算。
3.感受数学与生活的密切联系,体会学习数学的必要性,提高学习数学的积极性。
课堂导入
1.12.5美元可以兑换多少元人民币?(1美元兑换人民币6.31元)
12.5×6.31≈78.88(元)
答:可以兑换78.88元人民币。
运用的是“四舍五入”法
2.做一套童装需要2.2米布,30米布最多可以做多少套这样的童装?
30÷2.2≈13(套)
答:最多可以做13套这样的童装。
运用的是“去尾法”
3.妈妈要装10kg油需要几个这样的油桶?
10÷4.5≈3(个)
答:需要3个这样的油桶。
运用的是“进一法”
探究新知
学校科技小组去日本参加活动,老师到银行把5000元人民币兑换成日元,能兑换多少日元?
中国银行
2012年10月X日
1美元兑换人民币6.31元
1欧元兑换人民币8.19元
1港元兑换人民币0.81元
1新元兑换人民币5.11元
100日元兑换人民币7.89元
100泰铢兑换人民币20.32元
方法一
7.89÷100=0.0789元
5000÷0.0789≈63371.36(日元)
每日元兑换多少元人民币
5000元人民币兑换63371.36日元
答:能兑换大约63371.36日元
方法二
633.7136×100=63371.36日元
5000÷7.89≈633.7136(日元)
5000元人民币里有多少个7.89元
5000元人民币兑换63371.36日元
用计算器计算,并说说你发现了什么?(结果保留两位小数)
5÷1.5
5÷1.4
5÷1.3
5÷1.2
5÷1.1
5÷1
5÷0.9
5÷0.8
5÷0.7
5÷0.6
小组合作任务:
1.每组3号同学对答案,其他同学倾听、纠正。
2.组长组织组员依次分享自己的发现,其他组员质疑、补充。
3.整理大家的发现,记录员做好记录。
4.汇报员准备汇报。
≈3.33
≈3.57
≈3.85
≈4.17
≈4.55
=5
≈5.56
=6.25
≈7.14
≈8.33
除数大于1,商比被除数小。
除数小于1,商比被除数大。
除数越接近1,商越接近被除数。
用计算器计算,并说说你发现了什么?(结果保留两位小数)
5÷1.5
5÷1.4
5÷1.3
5÷1.2
5÷1.1
5÷1
5÷0.9
5÷0.8
5÷0.7
5÷0.6
发现
课堂练习
1.根据所学的规律,不计算,判断大小。
1.5÷1.1
<
1.5
3.5÷1
>
3.5
5.7÷1.2
<
5.7
1.25÷0.9
>
1.25
想一想,填一填。
算一算,你发现了什么?请你再写出一组类似的算式。
10÷0.8
10÷0.9
10÷1
10÷1.1
10÷1.2
10÷1.3
=12.5
≈11.11
=10
≈9.09
≈8.33
≈7.69
发现:当除数大于1时,商小于被除数;当除数小于
1时,商大于被除数;当除数接近1时,商也接
近被除数;当除数等于1时,商等于被除数。
想一想,算一算,你有什么发现?
12÷1.2
12÷1.2÷1.2
12÷1.2÷1.2÷1.2
=10
≈8.33
≈6.94
(1)
12÷0.8
12÷0.8÷0.8
12÷0.8÷0.8÷0.8
=15
=18.75
=23.4375
(2)
当除数大于1时,对同一个除数相除的次数越多,商越小;反之,商越大。
你能再写出一组类似算式说明你的发现吗?
课堂小结
当除数大于1时,商小于被除数;当除数小于1时,商大于被除数;当除数接近1时,商也接近被除数;当除数等于1时,商等于被除数.
课堂作业
1.按照1美元兑换6.31元人民币,美国籍教师安迪在中国工作,每月工资5000元,到银行能兑换多少美元?(保留两位小数)
5000÷6.31≈792.39(美元)
答:能兑换792.39美元。
2.想一想,算一算,通过这两组计算你有什么发现?
24÷1.2
24÷1.2÷1.2
24÷1.2÷1.2÷1.2
=20
≈16.67
≈13.89
(1)
24÷0.8
24÷0.8÷0.8
24÷0.8÷0.8÷0.8
=30
=37.5
=46.875
(2)
发现:当除数大于1时,对同一个除数相除的次数越多,商越小;反之,商越大。
同课章节目录
- 一 小数除法
- 1 精打细算
- 2 打扫卫生
- 3 谁打电话的时间长
- 4 人民币兑换
- 5 除得尽吗
- 6 调查“生活垃圾”
- 二 轴对称和平移
- 1 轴对称再认识(一)
- 2 轴对称再认识(二)
- 3 平移
- 4 欣赏与设计
- 三 倍数与因数
- 1 倍数与因数
- 2 探索活动:2、5的倍数的特征
- 3 探索活动:3的倍数的特征
- 4 找因数
- 5 找质数
- 四 多边形的面积
- 1 比较图形的面积
- 2 认识底和高
- 3 探索活动:平行四边形的面积
- 4 探索活动:三角形的面积
- 5 探索活动:梯形的面积
- 五 分数的意义
- 1 分数的再认识(一)
- 2 分数的再认识(二)
- 3 分饼
- 4 分数与除法
- 5 分数基本性质
- 6 找最大的公因数
- 7 约分
- 8 找最小的公倍数
- 9 分数的大小
- 六 组合图形的面积
- 1 组合图形的面积
- 2 探索活动:成长的脚印
- 3 公顷、平方千米
- 数学好玩
- 1 设计秋游方案
- 2 图形中的规律
- 3 尝试与猜测
- 七 可能性
- 1 谁先走
- 2 摸球游戏
