第四章 图形的平移与旋转单元测试题(含答案)
文档属性
| 名称 | 第四章 图形的平移与旋转单元测试题(含答案) | 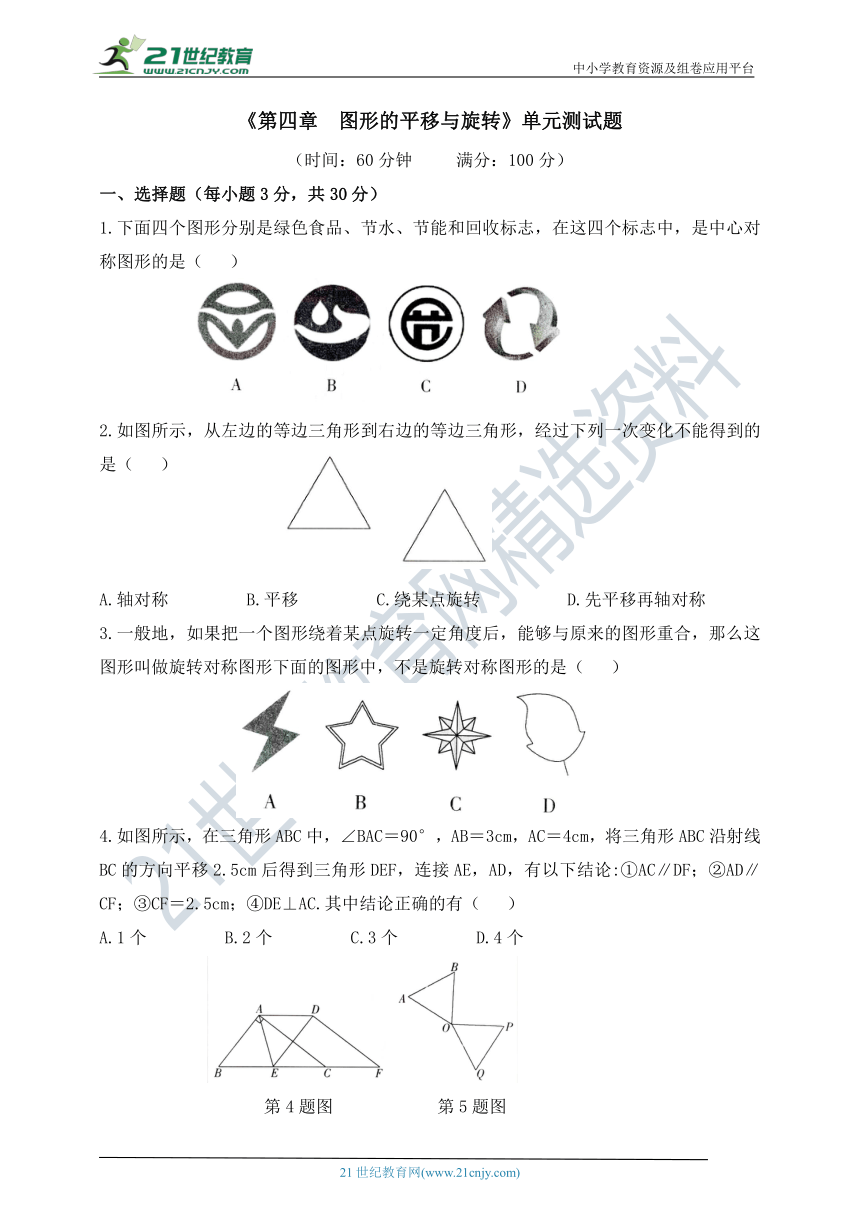 | |
| 格式 | doc | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-17 18:36:17 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
《第四章 图形的平移与旋转》单元测试题
(时间:60分钟 满分:100分)
一、选择题(每小题3分,共30分)
1.下面四个图形分别是绿色食品、节水、节能和回收标志,在这四个标志中,是中心对称图形的是( )
2.如图所示,从左边的等边三角形到右边的等边三角形,经过下列一次变化不能得到的是( )
A.轴对称 B.平移 C.绕某点旋转 D.先平移再轴对称
3.一般地,如果把一个图形绕着某点旋转一定角度后,能够与原来的图形重合,那么这图形叫做旋转对称图形下面的图形中,不是旋转对称图形的是( )
4.如图所示,在三角形ABC中,∠BAC=90°,AB=3cm,AC=4cm,将三角形ABC沿射线BC的方向平移2.5cm后得到三角形DEF,连接AE,AD,有以下结论:①AC∥DF;②AD∥CF;③CF=2.5cm;④DE⊥AC.其中结论正确的有( )
A.1个 B.2个 C.3个 D.4个
第4题图 第5题图
5.如图所示,已知△OAB是正三角形,OP⊥OB,OP=OA,将△OAB绕点O按顺时针方向旋转,使得OA与OP重合,得到△OPQ,则旋转的角度是( )
A.60° B.90° C.120° D.150°
6.经过下列变换,不能由图①所示的基本图形得到图②的是( )
A.旋转 B.中心对称和轴对称 C.平移和轴对称 D.中心对称
7.将△ABC绕原点旋转180°得到△ABC,设点A的坐标为(a,b),则点A′的坐标为
( )
A.(-a,-b) B.(a,-b) C.(-a,b) D.(a,b)
8.如图所示,Rt△ABC中,∠C=90°,BC=3,AC=4,将△ABC绕点B逆时针旋转得△A′BC′,若点C′在AB上,则AA′的长为( )
A. B.4 C. D.5
9.如图所示,在△ABC中,AB=5,BC=8,∠B=60°,先将△ABC沿射线BC的方向平移,得到△A′B'C′,再将△A′B'C′绕点A′逆时针旋转一定角度后,点B′恰好与点C重合,则平移的距离为( )
A.2 B.3 C.4 D.5
10.把一副三角板按图甲所示的方式放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,AB=12,DC=14,把三角板DCE绕点C顺时针旋转15°得到△D1CE1(如图乙),AB与CD1交于点O,连接AD1,则线段AD1的长为( )
A.6 B.10 C.8 D.
二、填空题(每小题3分,共24分)
11.如果 经过某种变换可以得到 ,那么 经过相同的变换可以得到___________.
12.平面直角坐标系中,已知点A的坐标为(m,3).若将点A先向下平移2个单位,再向左平移1个单位后得到点B(1,n),则m+n=__________.
13.如图所示,将Rt△ABC绕直角顶点C顺时针旋转90°,得到Rt△A′B'C,连接AA′,若∠1=25°,则∠BAC的度数是__________.
14.如图所示,已知点A(3,0),B(1,4),C(3,-2),D(7,0),连接AB,CD,将线段AB绕着某一点旋转一定角度,使A,B分别与C,D重合,则旋转中心的坐标为___________.
15.如图所示,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,将△ABC绕点A逆时针旋转得到△AB'C′,点B、C的对应点分别为点B′、C′,AB′与BC相交于点D,当B'C′∥AB时,CD=__________.
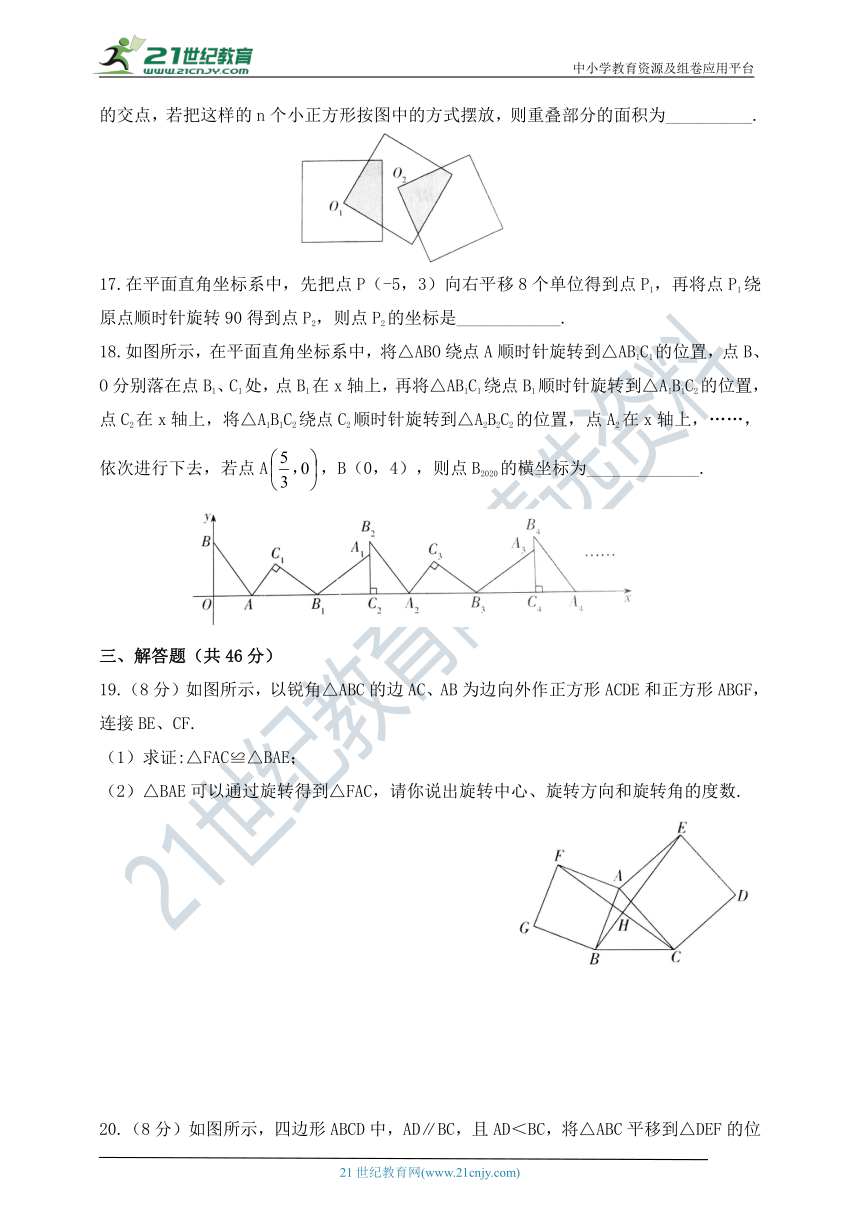
16.如图所示,三个边长均为2的正方形重叠在一起,O1,O2是其中两个正方形的对角线的交点,若把这样的n个小正方形按图中的方式摆放,则重叠部分的面积为__________.
17.在平面直角坐标系中,先把点P(-5,3)向右平移8个单位得到点P1,再将点P1绕原点顺时针旋转90得到点P2,则点P2的坐标是____________.
18.如图所示,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,……,依次进行下去,若点A,B(0,4),则点B2020的横坐标为_____________.
三、解答题(共46分)
19.(8分)如图所示,以锐角△ABC的边AC、AB为边向外作正方形ACDE和正方形ABGF,连接BE、CF.
(1)求证:△FAC≌△BAE;
(2)△BAE可以通过旋转得到△FAC,请你说出旋转中心、旋转方向和旋转角的度数.
20.(8分)如图所示,四边形ABCD中,AD∥BC,且AD<BC,将△ABC平移到△DEF的位置.
(1)指出平移的方向和平移的距离;
(2)试说明:AD+BC=BF.
21.(10分)如图所示,在Rt△ABC中,∠ACB=90°,点D、E分别在AB、AC上,CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得到线段CF,连接EF.
(1)补全图形;
(2)若EF∥CD,求证:∠BDC=90°.
22.(10分)如图所示,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3,5),B(-2,1),C(-1,3).
(1)若△ABC经过平移后得到△A1B1C1,已知点C1的坐标为(4,0),写出顶点A1、B1的坐标并画出△A1B1C1;
(2)画出△A2B2C2,使它与△ABC关于原点O成中心对称,并写出△A2B2C2的各顶点的坐标;
(3)作△ABC绕着点O按顺时针方向旋转90°得到的△A3B3C3,写出△A3B3C3的各顶点的坐标.
23.(10分)已知△ABC与△DEC是两个大小不同的等腰直角三角形.
(1)如图①所示,连接AE、DB.试判断线段AE和DB之间的数量关系和位置关系,并说明理由;
(2)如图②所示,连接DB,将线段DB绕点D顺时针旋转90°后得到线段DF,连接AF,试判断线段DE和AF之间的数量关系和位置关系,并说明理由.
参考答案
一、选择题
1.D 2.A 3.D 4.D 5.D 6.D 7.A 8.C 9.B 10.B
二、填空题
11. 12. 3 13. 20° 14.(2,-1) 15. 16. n-1
17.(3,-3) 18. 10 100
三、解答题
19.解析 (1)证明: ∵四边形ABGF和四边形ACDE是正方形,∴AF=AB, AC=AE,
∵∠BAF=∠CAE=90°,∴∠BAF+∠BAC=∠CAE+∠BAC,即∠FAC=∠BAE
在△FAC和△BAE中,∴△FAC≌△BAE(SAS).
(2)将△BAE以点A为旋转中心,顺时针旋转90°可以得到△FAC,故旋转中心为点A,旋转方向为顺时针,旋转角的度数为90°.
20.解析 (1)平移的方向是点A到点D的方向,平移的距离是线段AD的长度.
(2)证明: ∵将△ABC平移到△DEF的位置,∴CF=AD,
∵CF+BC=BF,∴AD+BC=BF.
21.解析(1)补全图形,如图所示.
(2)证明:由旋转的性质得∠DCF=90°,DC=FC,∴∠DCE+∠ECF=90°,
∵∠ACB=90°,∴∠DCE+∠BCD=90°,∴∠ECF=∠BCD.0
∵EF∥DC,∴∠EFC+∠DCF=180°,∴∠EFC=90°.
在△BDC和△EFC中,∴△BDC≌△EFC(SAS),∴∠BDC=∠EFC=90°.
22.解析 (1)由点C(-1,3)平移后的对应点C1的坐标为(4,0)可知,将△ABC向右平移5个单位,向下平移3个单位后得到△A1B1C1,△A1B1C1如图所示,A1(2,2),B1(3,-2).
(2)△A2B2C2如图所示,A2(3,-5),B2(2,-1),C2(1,-3).
(3)△A3B3C3如图所示,A3(5,3),B3(1,2),C3(3,1).
23.解析 (1)AE=DB,AE⊥DB理由如下:
∵△ABC与△DEC是等腰直角三角形,∴BC=AC,CD=CE,∠BCD=∠ACE,
∴Rt△BCD≌Rt△ACE∴AE=BD,∠AEC=∠BDC.
如图1,延长DB交AE于点M,
∵∠AEC+∠EAC=90°,∴∠BDC+∠EAC=90°,
∴在△AMD中,∠AMD=180-90°=90°,即AE⊥DB.
(2)DE=AF,DE⊥AF理由如下:
由题意易知,BE=AD
如图2,设ED与AF交于点N,
图2
∵∠EBD=∠C+∠BDC=90°+∠BDC,∠ADF=∠BDF+∠BDC=90°+∠BDC,
∴∠EBD=∠ADF.
在△EBD和△ADF中,∵∴△EBD≌△ADF,∴DE=AF,∠E=∠FAD,
∵∠E=45°,∠FAD=∠EDC=45°,
∴在△AND中,∠AND=180°-45°-45°=90°,即DE⊥AF.
_21?????????è?????(www.21cnjy.com)_
《第四章 图形的平移与旋转》单元测试题
(时间:60分钟 满分:100分)
一、选择题(每小题3分,共30分)
1.下面四个图形分别是绿色食品、节水、节能和回收标志,在这四个标志中,是中心对称图形的是( )
2.如图所示,从左边的等边三角形到右边的等边三角形,经过下列一次变化不能得到的是( )
A.轴对称 B.平移 C.绕某点旋转 D.先平移再轴对称
3.一般地,如果把一个图形绕着某点旋转一定角度后,能够与原来的图形重合,那么这图形叫做旋转对称图形下面的图形中,不是旋转对称图形的是( )
4.如图所示,在三角形ABC中,∠BAC=90°,AB=3cm,AC=4cm,将三角形ABC沿射线BC的方向平移2.5cm后得到三角形DEF,连接AE,AD,有以下结论:①AC∥DF;②AD∥CF;③CF=2.5cm;④DE⊥AC.其中结论正确的有( )
A.1个 B.2个 C.3个 D.4个
第4题图 第5题图
5.如图所示,已知△OAB是正三角形,OP⊥OB,OP=OA,将△OAB绕点O按顺时针方向旋转,使得OA与OP重合,得到△OPQ,则旋转的角度是( )
A.60° B.90° C.120° D.150°
6.经过下列变换,不能由图①所示的基本图形得到图②的是( )
A.旋转 B.中心对称和轴对称 C.平移和轴对称 D.中心对称
7.将△ABC绕原点旋转180°得到△ABC,设点A的坐标为(a,b),则点A′的坐标为
( )
A.(-a,-b) B.(a,-b) C.(-a,b) D.(a,b)
8.如图所示,Rt△ABC中,∠C=90°,BC=3,AC=4,将△ABC绕点B逆时针旋转得△A′BC′,若点C′在AB上,则AA′的长为( )
A. B.4 C. D.5
9.如图所示,在△ABC中,AB=5,BC=8,∠B=60°,先将△ABC沿射线BC的方向平移,得到△A′B'C′,再将△A′B'C′绕点A′逆时针旋转一定角度后,点B′恰好与点C重合,则平移的距离为( )
A.2 B.3 C.4 D.5
10.把一副三角板按图甲所示的方式放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,AB=12,DC=14,把三角板DCE绕点C顺时针旋转15°得到△D1CE1(如图乙),AB与CD1交于点O,连接AD1,则线段AD1的长为( )
A.6 B.10 C.8 D.
二、填空题(每小题3分,共24分)
11.如果 经过某种变换可以得到 ,那么 经过相同的变换可以得到___________.
12.平面直角坐标系中,已知点A的坐标为(m,3).若将点A先向下平移2个单位,再向左平移1个单位后得到点B(1,n),则m+n=__________.
13.如图所示,将Rt△ABC绕直角顶点C顺时针旋转90°,得到Rt△A′B'C,连接AA′,若∠1=25°,则∠BAC的度数是__________.
14.如图所示,已知点A(3,0),B(1,4),C(3,-2),D(7,0),连接AB,CD,将线段AB绕着某一点旋转一定角度,使A,B分别与C,D重合,则旋转中心的坐标为___________.
15.如图所示,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,将△ABC绕点A逆时针旋转得到△AB'C′,点B、C的对应点分别为点B′、C′,AB′与BC相交于点D,当B'C′∥AB时,CD=__________.
16.如图所示,三个边长均为2的正方形重叠在一起,O1,O2是其中两个正方形的对角线的交点,若把这样的n个小正方形按图中的方式摆放,则重叠部分的面积为__________.
17.在平面直角坐标系中,先把点P(-5,3)向右平移8个单位得到点P1,再将点P1绕原点顺时针旋转90得到点P2,则点P2的坐标是____________.
18.如图所示,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,……,依次进行下去,若点A,B(0,4),则点B2020的横坐标为_____________.
三、解答题(共46分)
19.(8分)如图所示,以锐角△ABC的边AC、AB为边向外作正方形ACDE和正方形ABGF,连接BE、CF.
(1)求证:△FAC≌△BAE;
(2)△BAE可以通过旋转得到△FAC,请你说出旋转中心、旋转方向和旋转角的度数.
20.(8分)如图所示,四边形ABCD中,AD∥BC,且AD<BC,将△ABC平移到△DEF的位置.
(1)指出平移的方向和平移的距离;
(2)试说明:AD+BC=BF.
21.(10分)如图所示,在Rt△ABC中,∠ACB=90°,点D、E分别在AB、AC上,CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得到线段CF,连接EF.
(1)补全图形;
(2)若EF∥CD,求证:∠BDC=90°.
22.(10分)如图所示,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3,5),B(-2,1),C(-1,3).
(1)若△ABC经过平移后得到△A1B1C1,已知点C1的坐标为(4,0),写出顶点A1、B1的坐标并画出△A1B1C1;
(2)画出△A2B2C2,使它与△ABC关于原点O成中心对称,并写出△A2B2C2的各顶点的坐标;
(3)作△ABC绕着点O按顺时针方向旋转90°得到的△A3B3C3,写出△A3B3C3的各顶点的坐标.
23.(10分)已知△ABC与△DEC是两个大小不同的等腰直角三角形.
(1)如图①所示,连接AE、DB.试判断线段AE和DB之间的数量关系和位置关系,并说明理由;
(2)如图②所示,连接DB,将线段DB绕点D顺时针旋转90°后得到线段DF,连接AF,试判断线段DE和AF之间的数量关系和位置关系,并说明理由.
参考答案
一、选择题
1.D 2.A 3.D 4.D 5.D 6.D 7.A 8.C 9.B 10.B
二、填空题
11. 12. 3 13. 20° 14.(2,-1) 15. 16. n-1
17.(3,-3) 18. 10 100
三、解答题
19.解析 (1)证明: ∵四边形ABGF和四边形ACDE是正方形,∴AF=AB, AC=AE,
∵∠BAF=∠CAE=90°,∴∠BAF+∠BAC=∠CAE+∠BAC,即∠FAC=∠BAE
在△FAC和△BAE中,∴△FAC≌△BAE(SAS).
(2)将△BAE以点A为旋转中心,顺时针旋转90°可以得到△FAC,故旋转中心为点A,旋转方向为顺时针,旋转角的度数为90°.
20.解析 (1)平移的方向是点A到点D的方向,平移的距离是线段AD的长度.
(2)证明: ∵将△ABC平移到△DEF的位置,∴CF=AD,
∵CF+BC=BF,∴AD+BC=BF.
21.解析(1)补全图形,如图所示.
(2)证明:由旋转的性质得∠DCF=90°,DC=FC,∴∠DCE+∠ECF=90°,
∵∠ACB=90°,∴∠DCE+∠BCD=90°,∴∠ECF=∠BCD.0
∵EF∥DC,∴∠EFC+∠DCF=180°,∴∠EFC=90°.
在△BDC和△EFC中,∴△BDC≌△EFC(SAS),∴∠BDC=∠EFC=90°.
22.解析 (1)由点C(-1,3)平移后的对应点C1的坐标为(4,0)可知,将△ABC向右平移5个单位,向下平移3个单位后得到△A1B1C1,△A1B1C1如图所示,A1(2,2),B1(3,-2).
(2)△A2B2C2如图所示,A2(3,-5),B2(2,-1),C2(1,-3).
(3)△A3B3C3如图所示,A3(5,3),B3(1,2),C3(3,1).
23.解析 (1)AE=DB,AE⊥DB理由如下:
∵△ABC与△DEC是等腰直角三角形,∴BC=AC,CD=CE,∠BCD=∠ACE,
∴Rt△BCD≌Rt△ACE∴AE=BD,∠AEC=∠BDC.
如图1,延长DB交AE于点M,
∵∠AEC+∠EAC=90°,∴∠BDC+∠EAC=90°,
∴在△AMD中,∠AMD=180-90°=90°,即AE⊥DB.
(2)DE=AF,DE⊥AF理由如下:
由题意易知,BE=AD
如图2,设ED与AF交于点N,
图2
∵∠EBD=∠C+∠BDC=90°+∠BDC,∠ADF=∠BDF+∠BDC=90°+∠BDC,
∴∠EBD=∠ADF.
在△EBD和△ADF中,∵∴△EBD≌△ADF,∴DE=AF,∠E=∠FAD,
∵∠E=45°,∠FAD=∠EDC=45°,
∴在△AND中,∠AND=180°-45°-45°=90°,即DE⊥AF.
_21?????????è?????(www.21cnjy.com)_
