北师大版九年级上册数学3.1.2用枚举法和列表法求概率 课件 (共20张PPT)
文档属性
| 名称 | 北师大版九年级上册数学3.1.2用枚举法和列表法求概率 课件 (共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-19 00:00:00 | ||
图片预览








文档简介
(共20张PPT)
3.1
用树状图或表格求概率
第2课时
用枚举法和列表法求概率
第三章
概率的进一步认识
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
用枚举法求概率
用列表法求概率
课时导入
复习提问
引出问题
1.什么叫事件的概率?
2.一般地,如果在一次试验中有n种可能结果,并且它们发生的可能性都相等,事件A包含其中的m种结果,那么事件A发生的概率P(A)
=
。
复
习
回
顾
知识点
用枚举法求概率
知1-导
感悟新知
1
1.
枚举法
:一个问题中,如果有优先的几种可能的情况,往往需要将这些可能的情况全部列举出来,逐个进行讨论.
这种方法就称为枚举.
2.
用枚举法求概率的步骤:
(1)列举出所有可能出现的结果;
(2)找出要求的事件的结果;
(3)利用公式求概率.
3.
要点精析:枚举时,考虑要全面,做到不重复、不遗漏.
感悟新知
例1:一个袋中有4个珠子,其中2个红色,2个蓝色,除颜色外其余特征均相同,若从这个袋中任取2个珠子,求都是蓝色珠子的概率.
知1-练
例
1
解:袋中4个珠子可以分别标记为H1,H2,L1,L2.
用“一一列举法”法求概率.
从袋中任取2个珠子的所有等可能的结果为(H1,H2),(H1,L1),(H1,L2),(H2,L1),(H2,L2),(L1,L2),共六种,其中都是蓝色珠子的结果只
有(L1,L2)一种,故P(都是蓝色珠子)=
知识点
用列表法求概率
知2-导
感悟新知
2
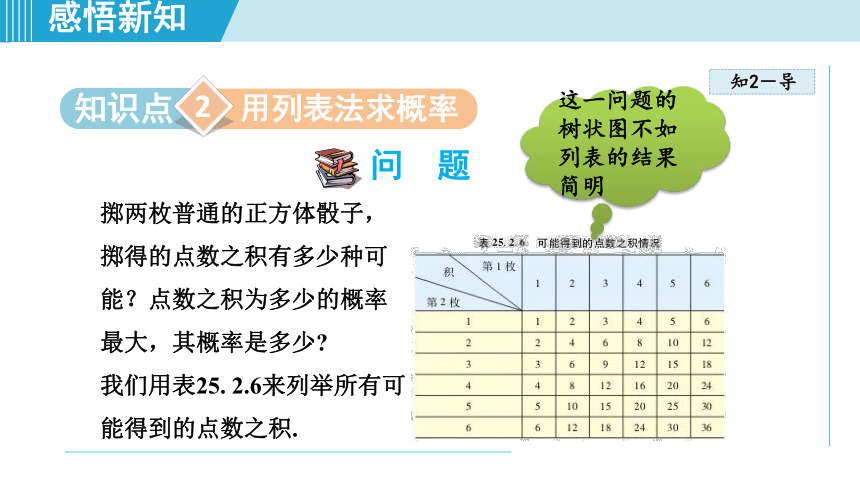
掷两枚普通的正方体骰子,掷得的点数之积有多少种可能?点数之积为多少的概率最大,其概率是多少?
我们用表25.
2.6来列举所有可能得到的点数之积.
这一问题的树状图不如列表的结果简明
问
题
知2-讲
感悟新知
列表法:
1.定义:用表格的形式反映事件发生的各种情况出现的
次数和方式,以及某一事件发生的次数和方式,并求
出概率的方法.
2.适用条件:如果事件中各种结果出现的可能性均等,含有两次操作(如掷骰子两次)或两个条件(如两个转盘)的事件.
3.列表的方法:选其中的一次操作或一个条件作为横行,
另一次操作或另一个条件为竖行,列表计算概率,如下示范表格:
知2-讲
感悟新知
感悟新知
知2-练
例2:一个盒子中装有两个红球、两个白球和一个蓝球,这些球除颜色外都相同.从中随机摸出一个球,记下颜色后放回,再从中随机摸出一个球,求两次摸到的球的颜色能配成紫色的概率.
例2
解:先将两个红球分别记作“红1”“红2”,两个白球分别记作“白1”“白2”,然后列表如下:
感悟新知
知2-练
第二次
第一次
红1
红2
白1
白2
蓝
红1
(红1,红1)
(红1,红2)
(红1,白1)
(红1,白2)
(红1,蓝)
红2
(红2,红1)
(红2,红2)
(红2,白1)
(红2,白2)
(红2,蓝)
白1
(白1,红1)
(白1,红2)
(白1,白1)
(白1,白2)
(白1,蓝)
白2
(白2,红1)
(白2,红2)
(白2,白1)
(白2,白2)
(白2,蓝)
蓝
(蓝,红1)
(蓝,红2)
(蓝,白1)
(蓝,白2)
(蓝,蓝)
感悟新知
知2-练
总共有25种结果,每种结果出现的可能性相同,而两次摸到的球的颜色能配成紫色的有结果有4种:(红1,蓝)(红2,蓝)(蓝,红1)(蓝,红2),
所以,P(能配成紫色)=
感悟新知
知2-练
例3:小莉的爸爸买了一张去音乐会的门票,她和哥哥两人都很想去,可门票只有一张,读九年级的哥哥想了一个办法,拿了八张扑克牌,将牌面为1,2,3,5的四张牌给小莉,将牌面为4,6,7,8的四张牌留给自己,并按如下游戏规则进行:小莉和哥哥从各自的四张牌中随机抽出一张,然后将抽出的两张扑克牌的牌面数字相加,如果和为偶数,则小莉去;如果和为奇数,则哥哥去.
(1)
请用列表的方法求小莉去听音乐会的概率;
(2)哥哥设计的游戏规则公平吗?若公平,请说明理由;若不公平,请你设计一种公平的游戏规则.
例
3
感悟新知
知2-练
导引:(1)
本题涉及两次抽牌,可通过列表求和找出所有可能的结果和关注的结果,再计算符合要求的概率;
(2)
判断游戏是否公平,主要看双方获胜的概率是否相同,若获胜的概率相同,则游戏公平,否则不公平.
感悟新知
知2-练
解:(1)列表如下:
由表格求出各方格中两数之和可知,所有等可能的结果有16种,其中和为偶数的有6种,所以
哥哥
小莉
4
6
7
8
1
(1,4)
(1,6)
(1,7)
(1,8)
2
(2,4)
(2,6)
(2,7)
(2,8)
3
(3,4)
(3,6)
(3,7)
(3,8)
5
(5,4)
(5,6)
(5,7)
(5,8)
感悟新知
知2-练
P(和为偶数)
P(和为奇数)
即小莉去听音乐会的概率为
(2)由(1)列表的结果可知:小莉去听音乐会的概率为
哥哥去听音乐会的概率为
两人获胜的概率不相等,所以游戏不公平,对哥哥有利.
游戏规则改为:若和为8或9或10,则小莉去;
若和为其他数,则哥哥去(修改的游戏规则答案不唯一,只要双方获胜的概率相等即可).
知2-讲
总
结
感悟新知
(1)对于两步试验(两个条件或两次操作)且可能出现的结果比较多时,用直接列举法易出错,为了不重不漏地列出所有可能的结果,用列表法较好.
(2)用列表法求概率的步骤:①列表;②通过表格计数,确定所有等可能的结果数n和关注的结果数m的值;③利用概率公式P(A)=
计算出事件的概率.
知2-讲
感悟新知
列表法与树状图法的联系与区别:
联系:应用列表法或树状图法求概率的共同前提是:
(1)
各种情况出现的可能性是相等的;
(2)
某事件发生的概率公式均为
(3)
在列出并计算各种情况出现的总次数和某事件
发生的次数时不能重复也不能遗漏.
知2-讲
感悟新知
区别:用树状图法或列表法时,当随机事件包含两步时,尤其是转转盘游戏问题,当其中一个转盘被等分成2份以上时,选用列表法比较方便,当然此时也可用树状图法;当随机事件包含三步或三步以上时,用树状图法方便,此时难以列表
课堂小结
概
率
枚举法和列表法一般适用于两个元素进行两步试验的题目,在列举可能的结果时,要分清“放回”与“不放回”两种情况.
必做:
请完成教材课后习题
课后作业
作业
3.1
用树状图或表格求概率
第2课时
用枚举法和列表法求概率
第三章
概率的进一步认识
逐点
导讲练
课堂小结
作业提升
学习目标
课时讲解
1
课时流程
2
用枚举法求概率
用列表法求概率
课时导入
复习提问
引出问题
1.什么叫事件的概率?
2.一般地,如果在一次试验中有n种可能结果,并且它们发生的可能性都相等,事件A包含其中的m种结果,那么事件A发生的概率P(A)
=
。
复
习
回
顾
知识点
用枚举法求概率
知1-导
感悟新知
1
1.
枚举法
:一个问题中,如果有优先的几种可能的情况,往往需要将这些可能的情况全部列举出来,逐个进行讨论.
这种方法就称为枚举.
2.
用枚举法求概率的步骤:
(1)列举出所有可能出现的结果;
(2)找出要求的事件的结果;
(3)利用公式求概率.
3.
要点精析:枚举时,考虑要全面,做到不重复、不遗漏.
感悟新知
例1:一个袋中有4个珠子,其中2个红色,2个蓝色,除颜色外其余特征均相同,若从这个袋中任取2个珠子,求都是蓝色珠子的概率.
知1-练
例
1
解:袋中4个珠子可以分别标记为H1,H2,L1,L2.
用“一一列举法”法求概率.
从袋中任取2个珠子的所有等可能的结果为(H1,H2),(H1,L1),(H1,L2),(H2,L1),(H2,L2),(L1,L2),共六种,其中都是蓝色珠子的结果只
有(L1,L2)一种,故P(都是蓝色珠子)=
知识点
用列表法求概率
知2-导
感悟新知
2
掷两枚普通的正方体骰子,掷得的点数之积有多少种可能?点数之积为多少的概率最大,其概率是多少?
我们用表25.
2.6来列举所有可能得到的点数之积.
这一问题的树状图不如列表的结果简明
问
题
知2-讲
感悟新知
列表法:
1.定义:用表格的形式反映事件发生的各种情况出现的
次数和方式,以及某一事件发生的次数和方式,并求
出概率的方法.
2.适用条件:如果事件中各种结果出现的可能性均等,含有两次操作(如掷骰子两次)或两个条件(如两个转盘)的事件.
3.列表的方法:选其中的一次操作或一个条件作为横行,
另一次操作或另一个条件为竖行,列表计算概率,如下示范表格:
知2-讲
感悟新知
感悟新知
知2-练
例2:一个盒子中装有两个红球、两个白球和一个蓝球,这些球除颜色外都相同.从中随机摸出一个球,记下颜色后放回,再从中随机摸出一个球,求两次摸到的球的颜色能配成紫色的概率.
例2
解:先将两个红球分别记作“红1”“红2”,两个白球分别记作“白1”“白2”,然后列表如下:
感悟新知
知2-练
第二次
第一次
红1
红2
白1
白2
蓝
红1
(红1,红1)
(红1,红2)
(红1,白1)
(红1,白2)
(红1,蓝)
红2
(红2,红1)
(红2,红2)
(红2,白1)
(红2,白2)
(红2,蓝)
白1
(白1,红1)
(白1,红2)
(白1,白1)
(白1,白2)
(白1,蓝)
白2
(白2,红1)
(白2,红2)
(白2,白1)
(白2,白2)
(白2,蓝)
蓝
(蓝,红1)
(蓝,红2)
(蓝,白1)
(蓝,白2)
(蓝,蓝)
感悟新知
知2-练
总共有25种结果,每种结果出现的可能性相同,而两次摸到的球的颜色能配成紫色的有结果有4种:(红1,蓝)(红2,蓝)(蓝,红1)(蓝,红2),
所以,P(能配成紫色)=
感悟新知
知2-练
例3:小莉的爸爸买了一张去音乐会的门票,她和哥哥两人都很想去,可门票只有一张,读九年级的哥哥想了一个办法,拿了八张扑克牌,将牌面为1,2,3,5的四张牌给小莉,将牌面为4,6,7,8的四张牌留给自己,并按如下游戏规则进行:小莉和哥哥从各自的四张牌中随机抽出一张,然后将抽出的两张扑克牌的牌面数字相加,如果和为偶数,则小莉去;如果和为奇数,则哥哥去.
(1)
请用列表的方法求小莉去听音乐会的概率;
(2)哥哥设计的游戏规则公平吗?若公平,请说明理由;若不公平,请你设计一种公平的游戏规则.
例
3
感悟新知
知2-练
导引:(1)
本题涉及两次抽牌,可通过列表求和找出所有可能的结果和关注的结果,再计算符合要求的概率;
(2)
判断游戏是否公平,主要看双方获胜的概率是否相同,若获胜的概率相同,则游戏公平,否则不公平.
感悟新知
知2-练
解:(1)列表如下:
由表格求出各方格中两数之和可知,所有等可能的结果有16种,其中和为偶数的有6种,所以
哥哥
小莉
4
6
7
8
1
(1,4)
(1,6)
(1,7)
(1,8)
2
(2,4)
(2,6)
(2,7)
(2,8)
3
(3,4)
(3,6)
(3,7)
(3,8)
5
(5,4)
(5,6)
(5,7)
(5,8)
感悟新知
知2-练
P(和为偶数)
P(和为奇数)
即小莉去听音乐会的概率为
(2)由(1)列表的结果可知:小莉去听音乐会的概率为
哥哥去听音乐会的概率为
两人获胜的概率不相等,所以游戏不公平,对哥哥有利.
游戏规则改为:若和为8或9或10,则小莉去;
若和为其他数,则哥哥去(修改的游戏规则答案不唯一,只要双方获胜的概率相等即可).
知2-讲
总
结
感悟新知
(1)对于两步试验(两个条件或两次操作)且可能出现的结果比较多时,用直接列举法易出错,为了不重不漏地列出所有可能的结果,用列表法较好.
(2)用列表法求概率的步骤:①列表;②通过表格计数,确定所有等可能的结果数n和关注的结果数m的值;③利用概率公式P(A)=
计算出事件的概率.
知2-讲
感悟新知
列表法与树状图法的联系与区别:
联系:应用列表法或树状图法求概率的共同前提是:
(1)
各种情况出现的可能性是相等的;
(2)
某事件发生的概率公式均为
(3)
在列出并计算各种情况出现的总次数和某事件
发生的次数时不能重复也不能遗漏.
知2-讲
感悟新知
区别:用树状图法或列表法时,当随机事件包含两步时,尤其是转转盘游戏问题,当其中一个转盘被等分成2份以上时,选用列表法比较方便,当然此时也可用树状图法;当随机事件包含三步或三步以上时,用树状图法方便,此时难以列表
课堂小结
概
率
枚举法和列表法一般适用于两个元素进行两步试验的题目,在列举可能的结果时,要分清“放回”与“不放回”两种情况.
必做:
请完成教材课后习题
课后作业
作业
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
