第二章 平行线与相交线 复习试题(无答案 )
文档属性
| 名称 | 第二章 平行线与相交线 复习试题(无答案 ) |

|
|
| 格式 | zip | ||
| 文件大小 | 284.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-06-04 00:00:00 | ||
图片预览

文档简介
兴宁市第二中学七年级数学下期周周练(五)
第二章:平行线与相交线
一:余角、补角、对顶角针对性训练:
1.已知:∠A= 300,则∠A的补角是________度.
2.如图l-2-1,直线AB,CD相交于点O,OE⊥AB于点O,OF平分∠AOE,∠ 1=15○30’,则下列结论中不正确的是( )
A.∠2 =450; B.∠1=∠3;
C.∠AOD与∠1互为补角; D.∠1的余角等于75030′
3._______的余角相等,_______的补角相等.
4.∠1和∠2互余,∠2和∠3互补,∠1=63○,∠3=______;
5.下列说法中正确的是( )
A.两个互补的角中必有一个是钝角; B.一个角的补角一定比这个角大;
C.互补的两个角中至少有一个角大于或等于直角; D.相等的角一定互余.
6.轮船航行到C处测得小岛A的方向为北偏东320,那么从A处观测到C处的方向为( )
A.南偏西320 B.东偏南320 C.南偏西580 D.东偏南580
7.若∠l=2∠2,且∠1+∠2=90○则∠1=___,∠2=___.
8.一个角的余角比它的补角的九分之二多1°,求这个角的度数.
9.∠1和∠2互余,∠2和∠3互补,∠3=1530,∠l=____________;
10.如图 l-2-2,AB⊥CD,AC⊥BC,图中与∠CAB互余的角有( )
A.0个 B.l个 C.2个 D.3个
11.如果一个角的补角是1500 ,那么这个角的余角是 _____;
12.已知∠A和∠B互余,∠A与∠C互补,∠B与∠C的和等于周角的,求∠A+∠B+∠C的度数.
13.如图如图1―2―3,已知∠AOC与∠B都是直角,∠BOC=590.
(1)求∠AOD的度数;
(2)求∠AOB和∠DOC的度数;
(3)∠A OB与∠DOC有何大小关系;
(4)若不知道∠BOC的具体度数,其他条件不变,这种关系仍然成立吗?
二:同位角、内错角、同旁内角的认识及平行线的性质针对性训练
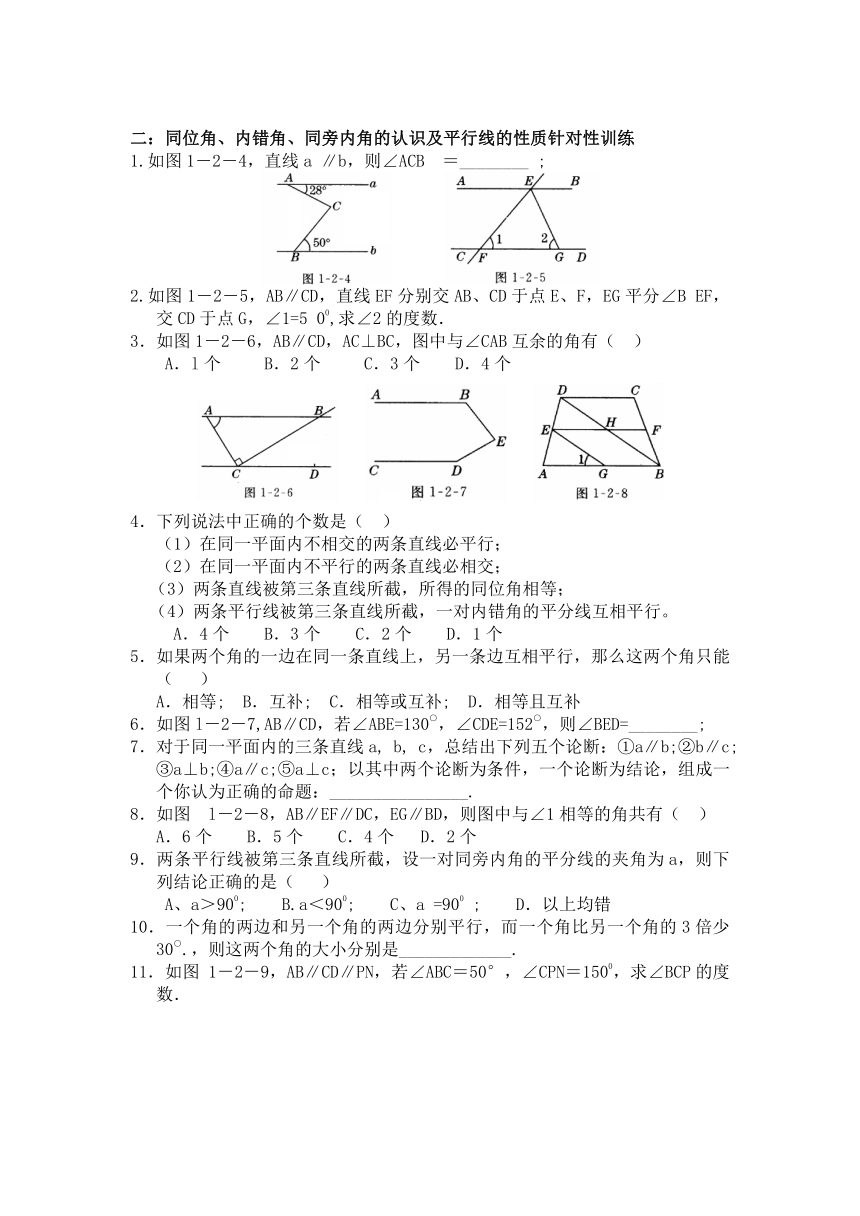
1.如图1―2―4,直线a ∥b,则∠ACB =________ ;
2.如图1―2―5,AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠B EF,交CD于点G,∠1=5 00,求∠2的度数.
3.如图1-2-6,AB∥CD,AC⊥BC,图中与∠CAB互余的角有( )
A.l个 B.2个 C.3个 D.4个
4.下列说法中正确的个数是( )
(1)在同一平面内不相交的两条直线必平行;
(2)在同一平面内不平行的两条直线必相交;
(3)两条直线被第三条直线所截,所得的同位角相等;
(4)两条平行线被第三条直线所截,一对内错角的平分线互相平行。
A.4个 B.3个 C.2个 D.1个
5.如果两个角的一边在同一条直线上,另一条边互相平行,那么这两个角只能( )
A.相等; B.互补; C.相等或互补; D.相等且互补
6.如图l-2-7,AB∥CD,若∠ABE=130○,∠CDE=152○,则∠BED=________;
7.对于同一平面内的三条直线a, b, c,总结出下列五个论断:①a∥b;②b∥c;③a⊥b;④a∥c;⑤a⊥c;以其中两个论断为条件,一个论断为结论,组成一个你认为正确的命题:________________.
8.如图 l-2-8,AB∥EF∥DC,EG∥BD,则图中与∠1相等的角共有( )
A.6个 B.5个 C.4个 D.2个
9.两条平行线被第三条直线所截,设一对同旁内角的平分线的夹角为a,则下列结论正确的是( )
A、a>900; B.a<900; C、a =900 ; D.以上均错
10.一个角的两边和另一个角的两边分别平行,而一个角比另一个角的3倍少30○.,则这两个角的大小分别是_____________.
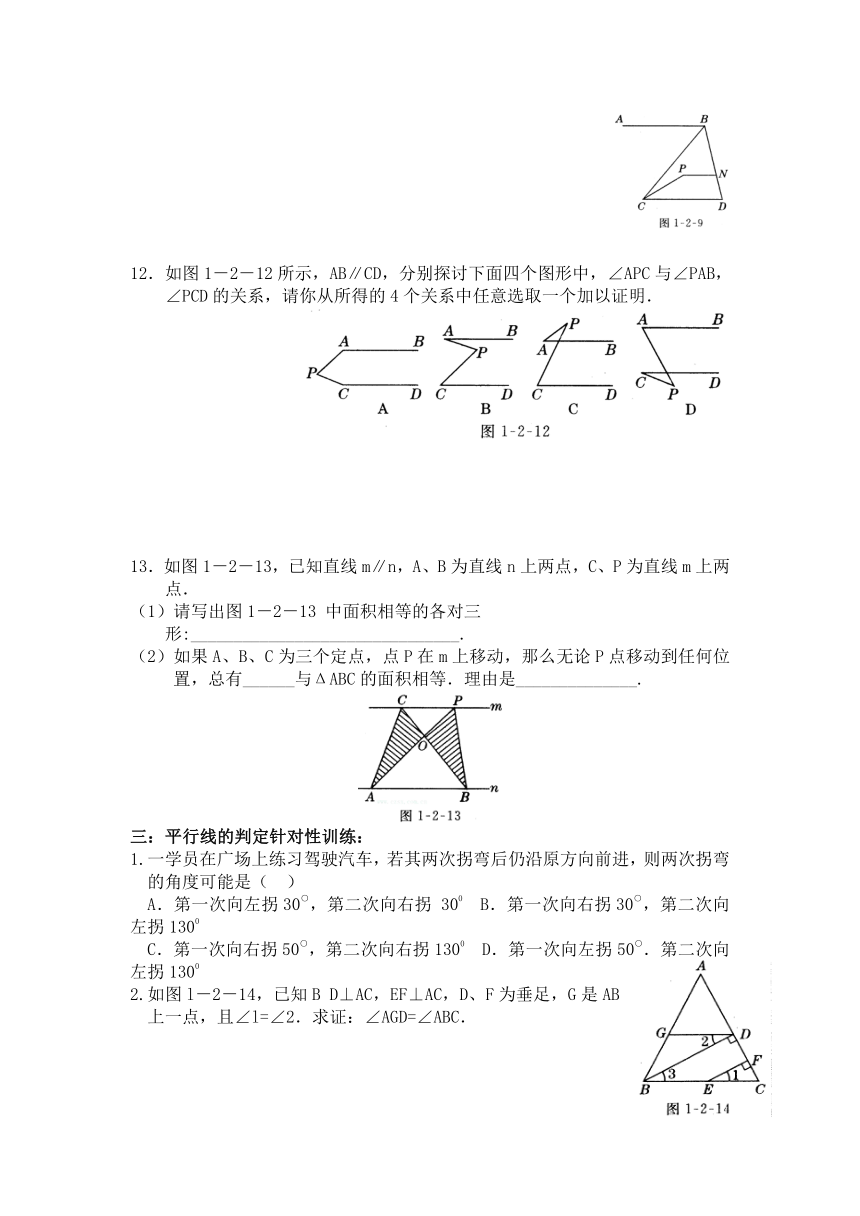
11.如图 1-2-9,AB∥CD∥PN,若∠ABC=50°,∠CPN=1500,求∠BCP的度数.
12.如图1-2-12所示,AB∥CD,分别探讨下面四个图形中,∠APC与∠PAB,∠PCD的关系,请你从所得的4个关系中任意选取一个加以证明.
13.如图1-2-13,已知直线m∥n,A、B为直线n上两点,C、P为直线m上两点.
(1)请写出图1-2-13 中面积相等的各对三形:_______________________________.
(2)如果A、B、C为三个定点,点P在m上移动,那么无论P点移动到任何位置,总有______与ΔABC的面积相等.理由是______________.
三:平行线的判定针对性训练:
1.一学员在广场上练习驾驶汽车,若其两次拐弯后仍沿原方向前进,则两次拐弯的角度可能是( )
A.第一次向左拐30○,第二次向右拐 300 B.第一次向右拐30○,第二次向左拐1300
C.第一次向右拐50○,第二次向右拐1300 D.第一次向左拐50○.第二次向左拐1300
2.如图l-2-14,已知B D⊥AC,EF⊥AC,D、F为垂足,G是AB上一点,且∠l=∠2.求证:∠AGD=∠ABC.
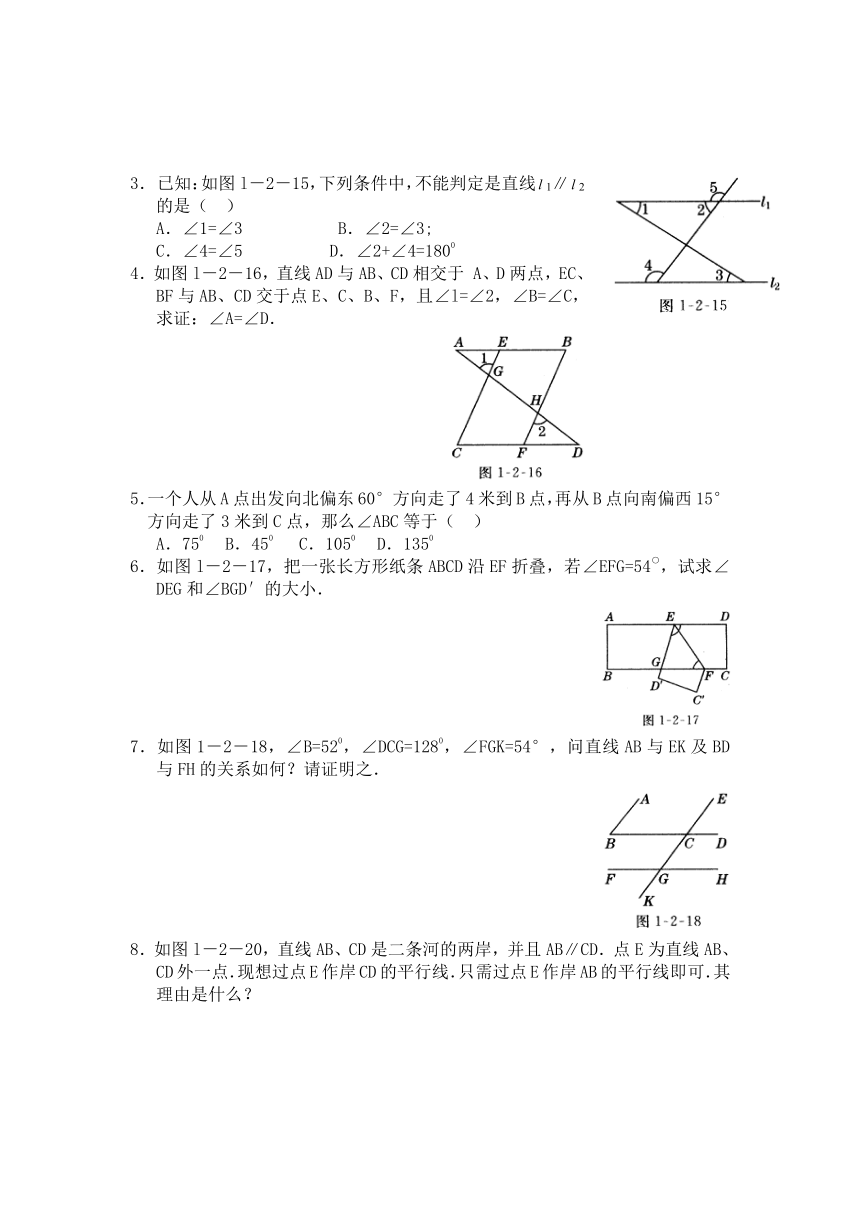
3. 已知:如图l-2-15,下列条件中,不能判定是直线1∥2的是( )
A.∠1=∠3 B.∠2=∠3;
C.∠4=∠5 D.∠2+∠4=1800
4.如图l-2-16,直线AD与AB、CD相交于 A、D两点,EC、BF与AB、CD交于点E、C、B、F,且∠l=∠2,∠B=∠C,求证:∠A=∠D.
5.一个人从A点出发向北偏东60°方向走了4米到B点,再从B点向南偏西15°方向走了3米到C点,那么∠ABC等于( )
A.750 B.450 C.1050 D.1350
6.如图l-2-17,把一张长方形纸条ABCD沿EF折叠,若∠EFG=54○,试求∠DEG和∠BGD′的大小.
7.如图1-2-18,∠B=520,∠DCG=1280,∠FGK=54°,问直线AB与EK及BD与FH的关系如何?请证明之.
8.如图l-2-20,直线AB、CD是二条河的两岸,并且AB∥CD.点E为直线AB、CD外一点.现想过点E作岸CD的平行线.只需过点E作岸AB的平行线即可.其理由是什么?
9.潜望镜中的两个镜子是互相平行放置的,如图l-2-39,光线经过镜子反射时∠l=∠2,∠3=∠4,请解释进人潜望镜和离开潜望镜的光线是平行的.
(Ⅱ)2005年新课标中考题一网打尽
(19分,10分钟)
1.(2005,金华,2分)如图1-2-22,直线a、b被直线所截,a∥b,如果∠1=500,那么∠2=____.
2.(2005、杭州.3分)在图l-2-23的几何体中,上下底面都是平行四边形,各个侧面都是梯形,那么图中和下底面平行的直线有( )
A.1条 B.2条 C.4条 D.8条
3.(2005、河南,3分)如图1-2-24,已知AB∥CD,EF分别交AB、CD于点E、F,∠l=70°,则∠2的度数是_________;
4.(2005、杭州,3分)“如果两条平行线被第三条直线所截得的八个角中.有一个角的度数已知,则( )”
A.只能求出其余三个角的度数; B.只能求出其余五个角的度数
C.只能求出其余六个角的度数; D.可以求出其余七个角的度数
5.(2005、福州,2分)如图1-2-25,两条直线a、b被第三条直线c所截,如果a∥b,∠1=70○,那么∠2=________.
6.(2005、湖北黄冈,3分)如图1-2-26,已知AB⊥CD,直线EF分别交AB、CD于点E、F,EG平分∠BEF,若∠l=500,则∠2的度数为( )
A.500 B.600 C.650 D.700
7.(2005、山东烟台,3分)如图l-2-27,一条公路修到湖边时,需拐弯绕湖而过;如果第一次拐的角∠A是1200,第二次拐的角∠B是1500第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C是( )
A.1200 B.1300 C.1400 D.1500
(Ⅲ)2006年中考题预测
(一)选择题(每小题 分,共 分)
1.已知两个角的两边分别平行,且其中一个角比另一个角的3倍多360,则这两个角的度数是( )
A.200和 960。 B.360和1440; C.400和1560 D.不能确定
2.如图l-2-28.已知AB∥CD.AP分别交AB、CD于A、C两点,CE平分∠DCF,∠1=1000 则∠2=( )
A.400 B.500 C.600 D.700
3.如图l-2-29,1∥2 ,AB⊥1,∠ABC=1300,则∠α=( )
A.600 B.500 C.400 D.300
4.如图l-2-30,直线c与直线地为相交,且a∥b,则下列结论:①∠l=∠2;②∠l=∠3;③∠3=∠2.正确的个数为( )
A.0 B.1 C.2 D.3
5.图l-2-31由三个火柴棒组成,移动其中一根.使得到的新图形有一组平行线,一组内错角,下列说法正确的是( )
①移动a,使a,b被c所截;②移动b.使b,c被a所截;③移动b,使b,a被c所截;④移动c使c、b被a所截.
A.①② B、②③ C、①③ D.①②③④
6.在同一平向内有2004条直线a1 a2 a3…a2004,如果a1⊥a2,a2∥a3,a3⊥a4,a4∥a5….那么a1与a2004,的位置关系是( )
A.垂直 B.平行;
C.相交但不垂直 D.以上都不对
(二)填空题(每题 4分,共 28分)
7.如图l-2-32所示,AB∥CD,EG⊥AB,垂足为G,若∠1=500,则∠E=_______.
8.如图l-2-33,已知∠l=∠2,∠A=1350,∠C=1000,则∠B=_______.
9.如图l-2-34,有一座山,想在山中开凿一条隧道直通甲、乙两地,在甲地测得隧道方向为北偏东41.50,如果甲、乙两地同时开工,要使隧道在山里准确打通.乙地隧道施工的角度为_______.
10.如图l-2-35所示.B、C是河岸上两点.A是对岸岸边上一点.测得∠ABC=45°,∠ACB=450.BC=60米,则点A到岸边BC的距离为____米.
11.如图l-2-36.已知A B∥CD,∠l=∠2.若∠l=500.则∠3=_____.
12.条直线和两条平行线中的一条垂直(或平行),那么这条直线也和另一条直线_______.
13.如果∠1和∠2是两条平行线1、2,被第三条直线3所截得的一对同位角,那么∠1和∠2的关系是__________.
二、学科内综合题(每题9分.共18分)
14.如图l-2-37,若∠3=∠l+∠2,试猜想A B与CD之间有何关系?
15.如图l-2-38,一块玻璃,A B∥CD.玻璃的下半部分打碎了,若量得上半部分中∠C=1200,∠D=95°,你能知道下半部分中的∠A和∠ B的度数吗?并说明理由.
三、跨学科渗透题(10分)
16.潜望镜中的两个镜子是互相平行放置的,如图l-2-39,光线经过镜子反射时∠l=∠2,∠3=∠4,请解释进人潜望镜和离开潜望镜的光线是平行的.
四、实际应用题(8分)
17.木工师傅用角尺画出工件边缘的两条垂线,问这两条垂线平行吗?请说明理由,如图l-2-40.
五、渗透新课标理念题门8题 8分,19题 16分,共 24分)
18.(探索题)如图l-2-41,从A地到 B地有①、②、③三条路可以走,每条路长分别为,m,n,则下列各式正确的是( )
A.>m>n B.>m>n
C.m<n=. D、>m=n
19.(探索规律题)根据补角和余角的定义可知:100的补角是1700,余角为800;150的补角是1650,余角为750;400的补角是1400,余角为500;520的补角为1280,余角为380……观察以上几组数据,你能得出怎样的结论?请用任意角α代替题中的100,150,4 00,5 20,来说明你的结论.
图 l-2-2
图1―2―3
第二章:平行线与相交线
一:余角、补角、对顶角针对性训练:
1.已知:∠A= 300,则∠A的补角是________度.
2.如图l-2-1,直线AB,CD相交于点O,OE⊥AB于点O,OF平分∠AOE,∠ 1=15○30’,则下列结论中不正确的是( )
A.∠2 =450; B.∠1=∠3;
C.∠AOD与∠1互为补角; D.∠1的余角等于75030′
3._______的余角相等,_______的补角相等.
4.∠1和∠2互余,∠2和∠3互补,∠1=63○,∠3=______;
5.下列说法中正确的是( )
A.两个互补的角中必有一个是钝角; B.一个角的补角一定比这个角大;
C.互补的两个角中至少有一个角大于或等于直角; D.相等的角一定互余.
6.轮船航行到C处测得小岛A的方向为北偏东320,那么从A处观测到C处的方向为( )
A.南偏西320 B.东偏南320 C.南偏西580 D.东偏南580
7.若∠l=2∠2,且∠1+∠2=90○则∠1=___,∠2=___.
8.一个角的余角比它的补角的九分之二多1°,求这个角的度数.
9.∠1和∠2互余,∠2和∠3互补,∠3=1530,∠l=____________;
10.如图 l-2-2,AB⊥CD,AC⊥BC,图中与∠CAB互余的角有( )
A.0个 B.l个 C.2个 D.3个
11.如果一个角的补角是1500 ,那么这个角的余角是 _____;
12.已知∠A和∠B互余,∠A与∠C互补,∠B与∠C的和等于周角的,求∠A+∠B+∠C的度数.
13.如图如图1―2―3,已知∠AOC与∠B都是直角,∠BOC=590.
(1)求∠AOD的度数;
(2)求∠AOB和∠DOC的度数;
(3)∠A OB与∠DOC有何大小关系;
(4)若不知道∠BOC的具体度数,其他条件不变,这种关系仍然成立吗?
二:同位角、内错角、同旁内角的认识及平行线的性质针对性训练
1.如图1―2―4,直线a ∥b,则∠ACB =________ ;
2.如图1―2―5,AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠B EF,交CD于点G,∠1=5 00,求∠2的度数.
3.如图1-2-6,AB∥CD,AC⊥BC,图中与∠CAB互余的角有( )
A.l个 B.2个 C.3个 D.4个
4.下列说法中正确的个数是( )
(1)在同一平面内不相交的两条直线必平行;
(2)在同一平面内不平行的两条直线必相交;
(3)两条直线被第三条直线所截,所得的同位角相等;
(4)两条平行线被第三条直线所截,一对内错角的平分线互相平行。
A.4个 B.3个 C.2个 D.1个
5.如果两个角的一边在同一条直线上,另一条边互相平行,那么这两个角只能( )
A.相等; B.互补; C.相等或互补; D.相等且互补
6.如图l-2-7,AB∥CD,若∠ABE=130○,∠CDE=152○,则∠BED=________;
7.对于同一平面内的三条直线a, b, c,总结出下列五个论断:①a∥b;②b∥c;③a⊥b;④a∥c;⑤a⊥c;以其中两个论断为条件,一个论断为结论,组成一个你认为正确的命题:________________.
8.如图 l-2-8,AB∥EF∥DC,EG∥BD,则图中与∠1相等的角共有( )
A.6个 B.5个 C.4个 D.2个
9.两条平行线被第三条直线所截,设一对同旁内角的平分线的夹角为a,则下列结论正确的是( )
A、a>900; B.a<900; C、a =900 ; D.以上均错
10.一个角的两边和另一个角的两边分别平行,而一个角比另一个角的3倍少30○.,则这两个角的大小分别是_____________.
11.如图 1-2-9,AB∥CD∥PN,若∠ABC=50°,∠CPN=1500,求∠BCP的度数.
12.如图1-2-12所示,AB∥CD,分别探讨下面四个图形中,∠APC与∠PAB,∠PCD的关系,请你从所得的4个关系中任意选取一个加以证明.
13.如图1-2-13,已知直线m∥n,A、B为直线n上两点,C、P为直线m上两点.
(1)请写出图1-2-13 中面积相等的各对三形:_______________________________.
(2)如果A、B、C为三个定点,点P在m上移动,那么无论P点移动到任何位置,总有______与ΔABC的面积相等.理由是______________.
三:平行线的判定针对性训练:
1.一学员在广场上练习驾驶汽车,若其两次拐弯后仍沿原方向前进,则两次拐弯的角度可能是( )
A.第一次向左拐30○,第二次向右拐 300 B.第一次向右拐30○,第二次向左拐1300
C.第一次向右拐50○,第二次向右拐1300 D.第一次向左拐50○.第二次向左拐1300
2.如图l-2-14,已知B D⊥AC,EF⊥AC,D、F为垂足,G是AB上一点,且∠l=∠2.求证:∠AGD=∠ABC.
3. 已知:如图l-2-15,下列条件中,不能判定是直线1∥2的是( )
A.∠1=∠3 B.∠2=∠3;
C.∠4=∠5 D.∠2+∠4=1800
4.如图l-2-16,直线AD与AB、CD相交于 A、D两点,EC、BF与AB、CD交于点E、C、B、F,且∠l=∠2,∠B=∠C,求证:∠A=∠D.
5.一个人从A点出发向北偏东60°方向走了4米到B点,再从B点向南偏西15°方向走了3米到C点,那么∠ABC等于( )
A.750 B.450 C.1050 D.1350
6.如图l-2-17,把一张长方形纸条ABCD沿EF折叠,若∠EFG=54○,试求∠DEG和∠BGD′的大小.
7.如图1-2-18,∠B=520,∠DCG=1280,∠FGK=54°,问直线AB与EK及BD与FH的关系如何?请证明之.
8.如图l-2-20,直线AB、CD是二条河的两岸,并且AB∥CD.点E为直线AB、CD外一点.现想过点E作岸CD的平行线.只需过点E作岸AB的平行线即可.其理由是什么?
9.潜望镜中的两个镜子是互相平行放置的,如图l-2-39,光线经过镜子反射时∠l=∠2,∠3=∠4,请解释进人潜望镜和离开潜望镜的光线是平行的.
(Ⅱ)2005年新课标中考题一网打尽
(19分,10分钟)
1.(2005,金华,2分)如图1-2-22,直线a、b被直线所截,a∥b,如果∠1=500,那么∠2=____.
2.(2005、杭州.3分)在图l-2-23的几何体中,上下底面都是平行四边形,各个侧面都是梯形,那么图中和下底面平行的直线有( )
A.1条 B.2条 C.4条 D.8条
3.(2005、河南,3分)如图1-2-24,已知AB∥CD,EF分别交AB、CD于点E、F,∠l=70°,则∠2的度数是_________;
4.(2005、杭州,3分)“如果两条平行线被第三条直线所截得的八个角中.有一个角的度数已知,则( )”
A.只能求出其余三个角的度数; B.只能求出其余五个角的度数
C.只能求出其余六个角的度数; D.可以求出其余七个角的度数
5.(2005、福州,2分)如图1-2-25,两条直线a、b被第三条直线c所截,如果a∥b,∠1=70○,那么∠2=________.
6.(2005、湖北黄冈,3分)如图1-2-26,已知AB⊥CD,直线EF分别交AB、CD于点E、F,EG平分∠BEF,若∠l=500,则∠2的度数为( )
A.500 B.600 C.650 D.700
7.(2005、山东烟台,3分)如图l-2-27,一条公路修到湖边时,需拐弯绕湖而过;如果第一次拐的角∠A是1200,第二次拐的角∠B是1500第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C是( )
A.1200 B.1300 C.1400 D.1500
(Ⅲ)2006年中考题预测
(一)选择题(每小题 分,共 分)
1.已知两个角的两边分别平行,且其中一个角比另一个角的3倍多360,则这两个角的度数是( )
A.200和 960。 B.360和1440; C.400和1560 D.不能确定
2.如图l-2-28.已知AB∥CD.AP分别交AB、CD于A、C两点,CE平分∠DCF,∠1=1000 则∠2=( )
A.400 B.500 C.600 D.700
3.如图l-2-29,1∥2 ,AB⊥1,∠ABC=1300,则∠α=( )
A.600 B.500 C.400 D.300
4.如图l-2-30,直线c与直线地为相交,且a∥b,则下列结论:①∠l=∠2;②∠l=∠3;③∠3=∠2.正确的个数为( )
A.0 B.1 C.2 D.3
5.图l-2-31由三个火柴棒组成,移动其中一根.使得到的新图形有一组平行线,一组内错角,下列说法正确的是( )
①移动a,使a,b被c所截;②移动b.使b,c被a所截;③移动b,使b,a被c所截;④移动c使c、b被a所截.
A.①② B、②③ C、①③ D.①②③④
6.在同一平向内有2004条直线a1 a2 a3…a2004,如果a1⊥a2,a2∥a3,a3⊥a4,a4∥a5….那么a1与a2004,的位置关系是( )
A.垂直 B.平行;
C.相交但不垂直 D.以上都不对
(二)填空题(每题 4分,共 28分)
7.如图l-2-32所示,AB∥CD,EG⊥AB,垂足为G,若∠1=500,则∠E=_______.
8.如图l-2-33,已知∠l=∠2,∠A=1350,∠C=1000,则∠B=_______.
9.如图l-2-34,有一座山,想在山中开凿一条隧道直通甲、乙两地,在甲地测得隧道方向为北偏东41.50,如果甲、乙两地同时开工,要使隧道在山里准确打通.乙地隧道施工的角度为_______.
10.如图l-2-35所示.B、C是河岸上两点.A是对岸岸边上一点.测得∠ABC=45°,∠ACB=450.BC=60米,则点A到岸边BC的距离为____米.
11.如图l-2-36.已知A B∥CD,∠l=∠2.若∠l=500.则∠3=_____.
12.条直线和两条平行线中的一条垂直(或平行),那么这条直线也和另一条直线_______.
13.如果∠1和∠2是两条平行线1、2,被第三条直线3所截得的一对同位角,那么∠1和∠2的关系是__________.
二、学科内综合题(每题9分.共18分)
14.如图l-2-37,若∠3=∠l+∠2,试猜想A B与CD之间有何关系?
15.如图l-2-38,一块玻璃,A B∥CD.玻璃的下半部分打碎了,若量得上半部分中∠C=1200,∠D=95°,你能知道下半部分中的∠A和∠ B的度数吗?并说明理由.
三、跨学科渗透题(10分)
16.潜望镜中的两个镜子是互相平行放置的,如图l-2-39,光线经过镜子反射时∠l=∠2,∠3=∠4,请解释进人潜望镜和离开潜望镜的光线是平行的.
四、实际应用题(8分)
17.木工师傅用角尺画出工件边缘的两条垂线,问这两条垂线平行吗?请说明理由,如图l-2-40.
五、渗透新课标理念题门8题 8分,19题 16分,共 24分)
18.(探索题)如图l-2-41,从A地到 B地有①、②、③三条路可以走,每条路长分别为,m,n,则下列各式正确的是( )
A.>m>n B.>m>n
C.m<n=. D、>m=n
19.(探索规律题)根据补角和余角的定义可知:100的补角是1700,余角为800;150的补角是1650,余角为750;400的补角是1400,余角为500;520的补角为1280,余角为380……观察以上几组数据,你能得出怎样的结论?请用任意角α代替题中的100,150,4 00,5 20,来说明你的结论.
图 l-2-2
图1―2―3
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
