沪科版(2019)高二物理选择性必修第一册《第2章机械振动》单元测试(含答案)
文档属性
| 名称 | 沪科版(2019)高二物理选择性必修第一册《第2章机械振动》单元测试(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 117.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-08-17 16:09:22 | ||
图片预览



文档简介
1122680011887200《第2章机械振动》单元测试
一、单选题
1.如图所示,振子以O点为平衡位置在A、B间做简谐运动,从振子第一次到达P点开始计时,则 (?? )
A.?振子第二次到达P点的时间间隔为一个周期
B.?振子第三次到达P点的时间间隔为一个周期
C.?振子第四次到达P点的时间间隔为一个周期
D.?振子从A点到B点或从B点到A点的时间间隔为一个周期
2.在“用单摆测定重力加速度”的实验中,用力传感器测得摆线的拉力大小F随时间t变化的图象如图所示,已知单摆的摆长为l,则重力加速度g为(??? )
A.?4π2lt2?????????????????????????????????????B.?π2lt2?????????????????????????????????????C.?4π2l9t2?????????????????????????????????????D.?π2l4t2
3.如图(甲)所示是用沙摆演示振动图象的实验装置,此装置可视为摆长为L的单摆,沙摆的运动可看作简谐运动,实验时在木板上留如图(甲)所示的结果。若用手拉木板做匀速运动,速度大小是0.20m/s。图(乙)所示的一段木板的长度是0.60m,那么这次实验所用沙摆对应的单摆长约为(?? )
A.?0.56m???????????????????????????????????B.?1.0m???????????????????????????????????C.?1.5m???????????????????????????????????D.?2.0m
4.如果把人作为一个有弹性的整体来看,在水平方向的固有频率约为3~6Hz,竖直方向的固有频率约为4~8Hz。为保障操作员的安全与健康,有关部门作出规定:用手操作的各类振动机械的频率应满足一定条件。根据以上提供的信息,下列条件规定合理的是(?? )
A.?各类振动机械的频率必须小于20Hz B.?各类振动机械的频率必须大于20Hz
C.?各类振动机械的频率应在3~6Hz D.?各类振动机械的频率应在4~8Hz
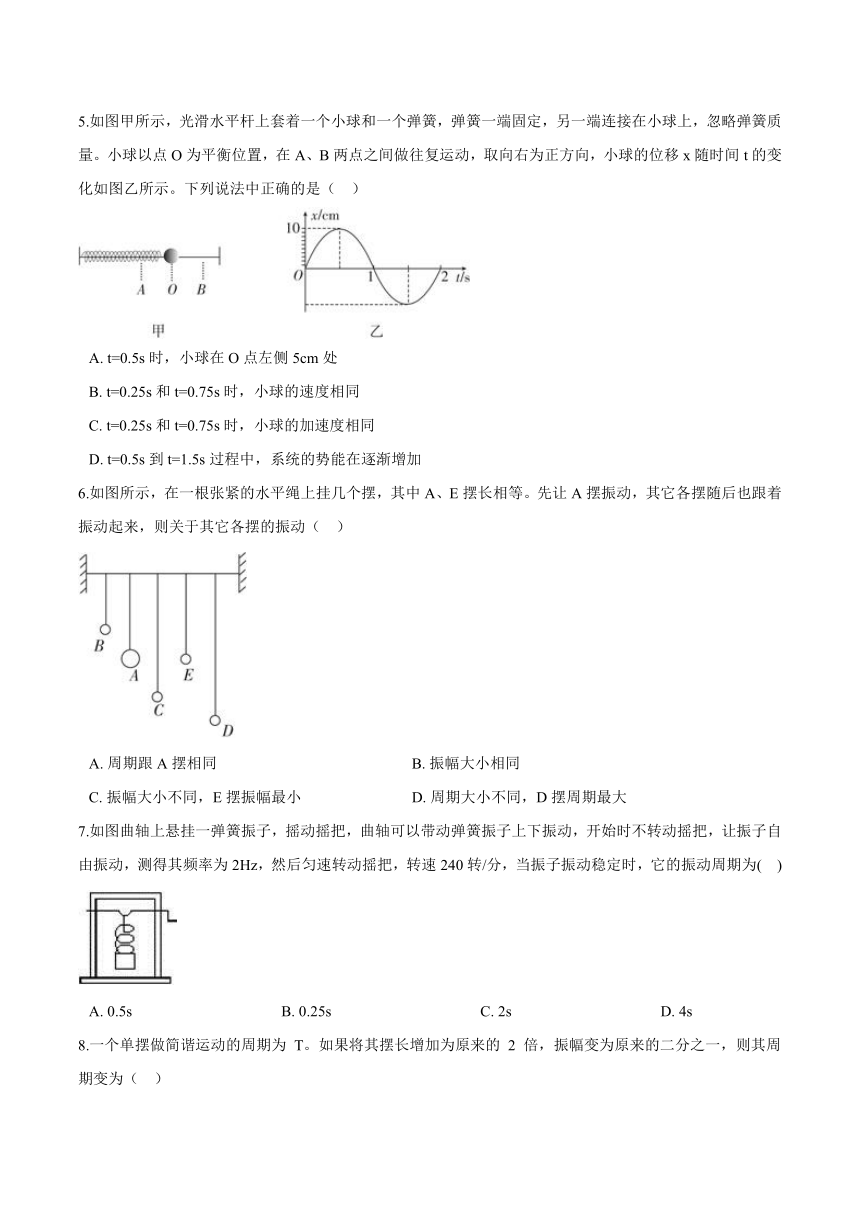
5.如图甲所示,光滑水平杆上套着一个小球和一个弹簧,弹簧一端固定,另一端连接在小球上,忽略弹簧质量。小球以点O为平衡位置,在A、B两点之间做往复运动,取向右为正方向,小球的位移x随时间t的变化如图乙所示。下列说法中正确的是(?? )
A.?t=0.5s时,小球在O点左侧5cm处
B.?t=0.25s和t=0.75s时,小球的速度相同
C.?t=0.25s和t=0.75s时,小球的加速度相同
D.?t=0.5s到t=1.5s过程中,系统的势能在逐渐增加
6.如图所示,在一根张紧的水平绳上挂几个摆,其中A、E摆长相等。先让A摆振动,其它各摆随后也跟着振动起来,则关于其它各摆的振动(?? )
A.?周期跟A摆相同 B.?振幅大小相同
C.?振幅大小不同,E摆振幅最小 D.?周期大小不同,D摆周期最大
7.如图曲轴上悬挂一弹簧振子,摇动摇把,曲轴可以带动弹簧振子上下振动,开始时不转动摇把,让振子自由振动,测得其频率为2Hz,然后匀速转动摇把,转速240转/分,当振子振动稳定时,它的振动周期为( ??)
A.?0.5s???????????????????????????????????????B.?0.25s???????????????????????????????????????C.?2s???????????????????????????????????????D.?4s
8.一个单摆做简谐运动的周期为 T。如果将其摆长增加为原来的 2 倍,振幅变为原来的二分之一,则其周期变为(?? )
A.?12T?????????????????????????????????????B.?2T2?????????????????????????????????????C.?2T?????????????????????????????????????D.?2T
9.如图甲所示,一个竖直圆盘转动时,固定在圆盘上的小圆柱带动一个T形支架在竖直方向振动,T形支架下面系着一个弹簧和小球组成的振动系统,当圆盘静止时,小球可稳定振动。改变圆盘匀速转动的周期,其共振曲线(振幅 A与驱动力的频率f的关系)如图乙所示。现使圆盘以4s的周期匀速转动,经过—段时间后,小球振动达到稳定,则下列说法正确的是(?? )
A.?此振动系统的固有频率约为0.25Hz
B.?此振动系统的振动频率约为3Hz
C.?若圆盘匀速转动的周期减小,系统的振动频率变大
D.?若圆盘匀速转动的周期增大,共振曲线的峰值将向左移动
10.如图所示为单摆在两次受迫振动中的共振曲线,下列说法正确的是(?? )
A.?若两次受迫振动分别在月球上和地球上进行,且摆长相等,则图线II是月球上的单摆共振曲线
B.?图线II若是在地球表面上完成的,则该摆摆长约为2m
C.?若摆长约为1m,则图线I是在地球表面上完成的
D.?若两次受迫振动均在地球上同一地点进行的,则两次摆长之比为l1:l2= 25:4
11.弹簧振子周期为2s,从振子通过平衡位置向右运动起,经过1.8s时,其运动情况是( )
A.?向右减速???????????????????????????B.?向右加速???????????????????????????C.?向左减速???????????????????????????D.?向左加速
12.如图所示,轻弹簧上端固定,下端连接一小物块,物块沿竖直方向做简谐运动。以竖直向上为正方向,物块做简谐运动的表达式为y=0.1sin5πt(m)。t=0时刻,一小球从距物块h 高处自由落下,t=0.3s时,小球恰好与物块处于同一高度,重力加速度g取10m/s2 , 空气阻力不计, 以下判断正确的是(?? )
A.?h=0.35 m??????????????????????????????????????????????????????????? B.?简谐运动的周期是 0.2 s
C.?0.3 s 内物块运动的路程是 0.1 m?????????????????????????D.?t=0.35s 时,物块与小球运动方向相同
二、填空题
13.如图所示,质量为m的木块放在轻弹簧上,与弹簧一起在竖直方向上做简谐运动。当振幅为A时,物体对弹簧的最大压力是物体重力的1.5 倍,则物体对弹簧的最小弹力为________; 要使物体在振动中不离开弹簧,振幅的最大值为________。
14.用单摆测定重力加速度的实验装置如图所示。
①为了减小误差,组装单摆时,应在下列器材中选用________(选填选项前的字母)
A.长度为30cm左右的细线 B.长度为1m左右的细线
C.直径为1.8cm的铁球 D.直径为1.8cm的塑料球
②测出悬点O到小球球心的距离(摆长)L及单摆完成n次全振动所用的时间t。请写出重力加速度的表达式g=________。
15.某同学利用单摆测定当地重力加速度,发现单摆静止时摆球重心在球心的正下方,他仍将从悬点到球心的距离当作摆长L,通过改变摆线的长度,测得6组L和对应的周期T,画出L一T2图线,然后在图线上选取A、B两个点,坐标如图所示.他采用恰当的数据处理方法,则计算重力加速度的表达式应为g=________.请你判断该同学得到的实验结果与摆球重心就在球心处的情况相比,将________.(填“偏大”、“偏小”或“相同”)
16.如图所示为一双线摆,它是在一水平天花板上用两根等长轻绳悬挂一小球而构成的,小球可视为质点,设图中的l和α为已知量,当小球垂直于纸面做简谐振动时,周期为________
三、解答题
17.如图所示,单摆摆长为L,摆球大小可忽略不计。现让摆球在竖直同一平面内做小角度摆动,在悬点O正下方 34L 的P处有一个小钉子。重力加速度为g,不计空气阻力,则其周期为多大?
18.一弹簧振子在水平方向上的MN之间做简谐运动,已知MN间的距离为10cm,振子在2s内完成了5次全振动。若从某时刻振子经过平衡位置时开始计时(t=0),经过 14 周期振子有负向最加速度。
(i)求振子的振幅和周期;
(ii)写出振子的振动方程。
19.一个摆长为2 m的单摆,在地球上某地振动时,测得完成100次全振动所用的时间为284 s.(计算结果保留三位有效数字)
①.求当地的重力加速度g;
②.把该单摆拿到月球上去,已知月球上的重力加速度是1.60 m/s2 , 则该单摆振动周期是多少?
答案
一、单选题
1.B 2.D 3.A 4.B 5.C 6.A 7.B 8.C 9.C 10.D 11.B 12.A
二、填空题
13.0.5mg;2A
14.BC;4π2Ln2t2
15.4π2(LB?LA)TB2?TA2;相同
16.2πlsinαg
三、解答题
17.解:该摆在通过悬点的竖直线两边的运动都可以看作简谐运动,则在碰到钉子前的周期为 T1=2πLg ,碰到钉子后摆长变为 L4 ,则周期为 T2=2πL4g=πLg
因此该摆的周期为 T=T12+T22=3π2Lg
18.解:(i)振幅 A=102cm=5cm
周期 T=52s=0.4s
(ii)设振动方程为 y=Asin(ωt+φ)
当t=0时,y=0,则 sinφ=0 得
φ=0 或 φ=π
经过 14 周期振子有负向最加速度,所以 φ=0 ,则 ω=2πT=5πrad/s
振动方程为 y=5sin(5πt)cm
19.解:①周期 T=tn=284100s=2.84s ?.
由周期公式 T=2πlg 得
g=4π2lT2=4×3.142×22.482m/s2≈9.78m/s2 ?
②由周期公式 T′=2πlg′ ??
代入数据解得 T'=2×3.14×21.60s≈7.02s
一、单选题
1.如图所示,振子以O点为平衡位置在A、B间做简谐运动,从振子第一次到达P点开始计时,则 (?? )
A.?振子第二次到达P点的时间间隔为一个周期
B.?振子第三次到达P点的时间间隔为一个周期
C.?振子第四次到达P点的时间间隔为一个周期
D.?振子从A点到B点或从B点到A点的时间间隔为一个周期
2.在“用单摆测定重力加速度”的实验中,用力传感器测得摆线的拉力大小F随时间t变化的图象如图所示,已知单摆的摆长为l,则重力加速度g为(??? )
A.?4π2lt2?????????????????????????????????????B.?π2lt2?????????????????????????????????????C.?4π2l9t2?????????????????????????????????????D.?π2l4t2
3.如图(甲)所示是用沙摆演示振动图象的实验装置,此装置可视为摆长为L的单摆,沙摆的运动可看作简谐运动,实验时在木板上留如图(甲)所示的结果。若用手拉木板做匀速运动,速度大小是0.20m/s。图(乙)所示的一段木板的长度是0.60m,那么这次实验所用沙摆对应的单摆长约为(?? )
A.?0.56m???????????????????????????????????B.?1.0m???????????????????????????????????C.?1.5m???????????????????????????????????D.?2.0m
4.如果把人作为一个有弹性的整体来看,在水平方向的固有频率约为3~6Hz,竖直方向的固有频率约为4~8Hz。为保障操作员的安全与健康,有关部门作出规定:用手操作的各类振动机械的频率应满足一定条件。根据以上提供的信息,下列条件规定合理的是(?? )
A.?各类振动机械的频率必须小于20Hz B.?各类振动机械的频率必须大于20Hz
C.?各类振动机械的频率应在3~6Hz D.?各类振动机械的频率应在4~8Hz
5.如图甲所示,光滑水平杆上套着一个小球和一个弹簧,弹簧一端固定,另一端连接在小球上,忽略弹簧质量。小球以点O为平衡位置,在A、B两点之间做往复运动,取向右为正方向,小球的位移x随时间t的变化如图乙所示。下列说法中正确的是(?? )
A.?t=0.5s时,小球在O点左侧5cm处
B.?t=0.25s和t=0.75s时,小球的速度相同
C.?t=0.25s和t=0.75s时,小球的加速度相同
D.?t=0.5s到t=1.5s过程中,系统的势能在逐渐增加
6.如图所示,在一根张紧的水平绳上挂几个摆,其中A、E摆长相等。先让A摆振动,其它各摆随后也跟着振动起来,则关于其它各摆的振动(?? )
A.?周期跟A摆相同 B.?振幅大小相同
C.?振幅大小不同,E摆振幅最小 D.?周期大小不同,D摆周期最大
7.如图曲轴上悬挂一弹簧振子,摇动摇把,曲轴可以带动弹簧振子上下振动,开始时不转动摇把,让振子自由振动,测得其频率为2Hz,然后匀速转动摇把,转速240转/分,当振子振动稳定时,它的振动周期为( ??)
A.?0.5s???????????????????????????????????????B.?0.25s???????????????????????????????????????C.?2s???????????????????????????????????????D.?4s
8.一个单摆做简谐运动的周期为 T。如果将其摆长增加为原来的 2 倍,振幅变为原来的二分之一,则其周期变为(?? )
A.?12T?????????????????????????????????????B.?2T2?????????????????????????????????????C.?2T?????????????????????????????????????D.?2T
9.如图甲所示,一个竖直圆盘转动时,固定在圆盘上的小圆柱带动一个T形支架在竖直方向振动,T形支架下面系着一个弹簧和小球组成的振动系统,当圆盘静止时,小球可稳定振动。改变圆盘匀速转动的周期,其共振曲线(振幅 A与驱动力的频率f的关系)如图乙所示。现使圆盘以4s的周期匀速转动,经过—段时间后,小球振动达到稳定,则下列说法正确的是(?? )
A.?此振动系统的固有频率约为0.25Hz
B.?此振动系统的振动频率约为3Hz
C.?若圆盘匀速转动的周期减小,系统的振动频率变大
D.?若圆盘匀速转动的周期增大,共振曲线的峰值将向左移动
10.如图所示为单摆在两次受迫振动中的共振曲线,下列说法正确的是(?? )
A.?若两次受迫振动分别在月球上和地球上进行,且摆长相等,则图线II是月球上的单摆共振曲线
B.?图线II若是在地球表面上完成的,则该摆摆长约为2m
C.?若摆长约为1m,则图线I是在地球表面上完成的
D.?若两次受迫振动均在地球上同一地点进行的,则两次摆长之比为l1:l2= 25:4
11.弹簧振子周期为2s,从振子通过平衡位置向右运动起,经过1.8s时,其运动情况是( )
A.?向右减速???????????????????????????B.?向右加速???????????????????????????C.?向左减速???????????????????????????D.?向左加速
12.如图所示,轻弹簧上端固定,下端连接一小物块,物块沿竖直方向做简谐运动。以竖直向上为正方向,物块做简谐运动的表达式为y=0.1sin5πt(m)。t=0时刻,一小球从距物块h 高处自由落下,t=0.3s时,小球恰好与物块处于同一高度,重力加速度g取10m/s2 , 空气阻力不计, 以下判断正确的是(?? )
A.?h=0.35 m??????????????????????????????????????????????????????????? B.?简谐运动的周期是 0.2 s
C.?0.3 s 内物块运动的路程是 0.1 m?????????????????????????D.?t=0.35s 时,物块与小球运动方向相同
二、填空题
13.如图所示,质量为m的木块放在轻弹簧上,与弹簧一起在竖直方向上做简谐运动。当振幅为A时,物体对弹簧的最大压力是物体重力的1.5 倍,则物体对弹簧的最小弹力为________; 要使物体在振动中不离开弹簧,振幅的最大值为________。
14.用单摆测定重力加速度的实验装置如图所示。
①为了减小误差,组装单摆时,应在下列器材中选用________(选填选项前的字母)
A.长度为30cm左右的细线 B.长度为1m左右的细线
C.直径为1.8cm的铁球 D.直径为1.8cm的塑料球
②测出悬点O到小球球心的距离(摆长)L及单摆完成n次全振动所用的时间t。请写出重力加速度的表达式g=________。
15.某同学利用单摆测定当地重力加速度,发现单摆静止时摆球重心在球心的正下方,他仍将从悬点到球心的距离当作摆长L,通过改变摆线的长度,测得6组L和对应的周期T,画出L一T2图线,然后在图线上选取A、B两个点,坐标如图所示.他采用恰当的数据处理方法,则计算重力加速度的表达式应为g=________.请你判断该同学得到的实验结果与摆球重心就在球心处的情况相比,将________.(填“偏大”、“偏小”或“相同”)
16.如图所示为一双线摆,它是在一水平天花板上用两根等长轻绳悬挂一小球而构成的,小球可视为质点,设图中的l和α为已知量,当小球垂直于纸面做简谐振动时,周期为________
三、解答题
17.如图所示,单摆摆长为L,摆球大小可忽略不计。现让摆球在竖直同一平面内做小角度摆动,在悬点O正下方 34L 的P处有一个小钉子。重力加速度为g,不计空气阻力,则其周期为多大?
18.一弹簧振子在水平方向上的MN之间做简谐运动,已知MN间的距离为10cm,振子在2s内完成了5次全振动。若从某时刻振子经过平衡位置时开始计时(t=0),经过 14 周期振子有负向最加速度。
(i)求振子的振幅和周期;
(ii)写出振子的振动方程。
19.一个摆长为2 m的单摆,在地球上某地振动时,测得完成100次全振动所用的时间为284 s.(计算结果保留三位有效数字)
①.求当地的重力加速度g;
②.把该单摆拿到月球上去,已知月球上的重力加速度是1.60 m/s2 , 则该单摆振动周期是多少?
答案
一、单选题
1.B 2.D 3.A 4.B 5.C 6.A 7.B 8.C 9.C 10.D 11.B 12.A
二、填空题
13.0.5mg;2A
14.BC;4π2Ln2t2
15.4π2(LB?LA)TB2?TA2;相同
16.2πlsinαg
三、解答题
17.解:该摆在通过悬点的竖直线两边的运动都可以看作简谐运动,则在碰到钉子前的周期为 T1=2πLg ,碰到钉子后摆长变为 L4 ,则周期为 T2=2πL4g=πLg
因此该摆的周期为 T=T12+T22=3π2Lg
18.解:(i)振幅 A=102cm=5cm
周期 T=52s=0.4s
(ii)设振动方程为 y=Asin(ωt+φ)
当t=0时,y=0,则 sinφ=0 得
φ=0 或 φ=π
经过 14 周期振子有负向最加速度,所以 φ=0 ,则 ω=2πT=5πrad/s
振动方程为 y=5sin(5πt)cm
19.解:①周期 T=tn=284100s=2.84s ?.
由周期公式 T=2πlg 得
g=4π2lT2=4×3.142×22.482m/s2≈9.78m/s2 ?
②由周期公式 T′=2πlg′ ??
代入数据解得 T'=2×3.14×21.60s≈7.02s
同课章节目录
- 第1章 碰撞与动量守恒
- 1.1 动量变化与冲量的关系
- 1.2 动量守恒定律
- 1.3 动量守恒定律的案例分析
- 1.4 美妙的守恒定律
- 第2章 机械振动
- 2.1 简谐运动
- 2.2 物体做简谐运动的原因
- 2.3 摆钟的物理原理
- 2.4 单摆振动的周期
- 2.5 受迫振动与共振
- 第3章 机械波
- 3.1 机械波的产生
- 3.2 机械波的描述
- 3.3 机械波案例分析
- 3.4 惠更斯原理 波的反射与折射
- 3.5 波的干涉与衍射
- 3.6 多普勒效应
- 第4章 光及其应用
- 4.1 光的折射
- 4.2 全反射与光导纤维
- 4.3 光的干涉
- 4.4 用双缝干涉仪测量光的波长
- 4.5 光的衍射
- 4.6 光的偏振与立体电影
- 4.7 激光
