七年级数学镶嵌
图片预览










文档简介
(共50张PPT)
欢迎走进数学世界
欢迎走进数学世界
欢迎走进数学世界
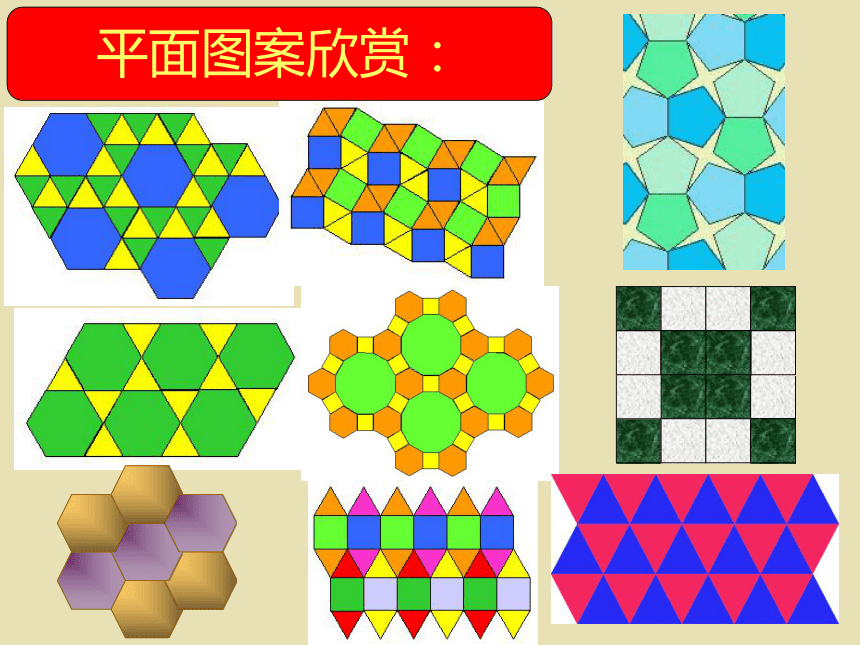
平面图案欣赏:
1、你能只用一种多边形(如正三角形,正四边形,正六边形)拼成一个地面吗?
2、你能只用一种正五边形拼成一个地面吗?
3、为什么正五边形拼不成地面?而用正三角形可以?可以拼成一个地面条件是什么?
4、试用数学知识推导,只用一种正多边形进行平面镶嵌,有几种方法?
5、任意的三角形,任意的四边形均可镶嵌成一个地面吗?
阅读课本,思考下列问题,并用纸片进行拼图试验
仔细观察以下图案,说明它们都是由哪些几何图形组成?
用形状相同或不同的平面封闭图形把一块平面既无缝隙又不重叠的全部覆盖叫平面镶嵌。
注意:镶嵌的原则是不重叠,又无空隙。
镶嵌平面图案需要的什么条件?
拼接在同一个点的各个角的和恰好等于360度
1
2
3
想一想
仅用一种正多边形镶嵌,哪几种正
多边形能镶嵌成一个平面?
探究问题(一)
要用几个形状、大小完全相同的图形不留空隙、不重叠地镶嵌一个平面,需使得拼接点处的各角之和为360°.
。
k ·
(n-2)×180
n
= 360
。
(n-2)(k-2)=4
k=6
n=3
k=4
n=4
k=3
n=6
设在一个顶点周围有 k 个正 n 边形的角,则有
∵ k 为正整数, n 为大于等于 3 的正整数
∴解为
用两种正多边形镶嵌,哪些能镶嵌成一个平面
探究问题(二)
2 m+3 n=12
m=3
n=2
m·60 +n·90 =360
。
。
。
设在一个顶点周围有 m 个正三角形的角,n 个正方形的角,
则有
∵ m,n 为正整数
∴解为
m+2 n=6
m=2
n=2
m=4
n=1
m·60 +n·120 =360
。
。
。
设在一个顶点周围有 m 个正三角形的角,n 个正六边形的角,
则有
∵ m,n 为正整数
∴解为
2 m+5 n=12
m=1
n=2
m·60 +n·150 =360
。
。
。
设在一个顶点周围有 m 个正三角形的角,n 个正十二边形
的角,则有
∵ m,n 为正整数
∴解为
2 m+3 n=8
m=1
n=2
m·90 +n·135 =360
。
。
。
设在一个顶点周围有个 m 正四边形的角,n 个正八边形
的角,则有
∵ m,n 为正整数
∴解为
设在一个顶点周围有 m 个正五边形的角,n 个正十边形的角,则有
3 m+4 n=10
m=2
n=1
m·108 +n·144 =360
。
。
。
∵ m,n 为正整数
∴解为
用三种正多边形镶嵌,哪些能
镶嵌成一个平面?
探究问题(三)
思考同一种任意三角形可否镶嵌成一个平面?
同一种任意四边形可否镶嵌成一个平面?
收 集 整 理 数 据 正n边形 拼图 每个内角的度数 使用正多边形的个数k 结论
能镶嵌
能镶嵌
不能镶嵌
不能镶嵌
能镶嵌
K= 6
K= 4
K= 3
K= 4
K= 3
60°
90°
108°
108°
120°
n =3
n =6
n =4
n =5
分 析 数 据 正n边形 拼图 每个内角的度数
与360°的关系 结论
n=3
n=4
n=5
n=6
能镶嵌
不能镶嵌
不能镶嵌
能镶嵌
6×60°= 360°
4×90°= 360°
4×108°> 360°
3×120°= 360°
3×108°< 360°
能镶嵌
练习题
1.能够用一种正多边形铺满地面的是____。
A 正五边形 B 正六边形
C 正七边形 D 正八边形
2.如果用正三角形进行镶嵌,那么在每个顶 点的周围有____个正三角形。
3.如果用正三角形和正六边形进行镶嵌,那 么在每个顶点的周围有____ 个正三角形和____个正六边形或 ____个正三角形和____ 个正六边形
B
6
2
2
4
1
1. 用一种正多边形镶嵌,哪些可以,分别是哪些正多边形?
2. 你能找到用两种正多边形镶嵌,还有哪些吗?请你设计一个用两个正多边形镶嵌的图形。
课后作业:
谢谢!
欢迎走进数学世界
欢迎走进数学世界
欢迎走进数学世界
平面图案欣赏:
1、你能只用一种多边形(如正三角形,正四边形,正六边形)拼成一个地面吗?
2、你能只用一种正五边形拼成一个地面吗?
3、为什么正五边形拼不成地面?而用正三角形可以?可以拼成一个地面条件是什么?
4、试用数学知识推导,只用一种正多边形进行平面镶嵌,有几种方法?
5、任意的三角形,任意的四边形均可镶嵌成一个地面吗?
阅读课本,思考下列问题,并用纸片进行拼图试验
仔细观察以下图案,说明它们都是由哪些几何图形组成?
用形状相同或不同的平面封闭图形把一块平面既无缝隙又不重叠的全部覆盖叫平面镶嵌。
注意:镶嵌的原则是不重叠,又无空隙。
镶嵌平面图案需要的什么条件?
拼接在同一个点的各个角的和恰好等于360度
1
2
3
想一想
仅用一种正多边形镶嵌,哪几种正
多边形能镶嵌成一个平面?
探究问题(一)
要用几个形状、大小完全相同的图形不留空隙、不重叠地镶嵌一个平面,需使得拼接点处的各角之和为360°.
。
k ·
(n-2)×180
n
= 360
。
(n-2)(k-2)=4
k=6
n=3
k=4
n=4
k=3
n=6
设在一个顶点周围有 k 个正 n 边形的角,则有
∵ k 为正整数, n 为大于等于 3 的正整数
∴解为
用两种正多边形镶嵌,哪些能镶嵌成一个平面
探究问题(二)
2 m+3 n=12
m=3
n=2
m·60 +n·90 =360
。
。
。
设在一个顶点周围有 m 个正三角形的角,n 个正方形的角,
则有
∵ m,n 为正整数
∴解为
m+2 n=6
m=2
n=2
m=4
n=1
m·60 +n·120 =360
。
。
。
设在一个顶点周围有 m 个正三角形的角,n 个正六边形的角,
则有
∵ m,n 为正整数
∴解为
2 m+5 n=12
m=1
n=2
m·60 +n·150 =360
。
。
。
设在一个顶点周围有 m 个正三角形的角,n 个正十二边形
的角,则有
∵ m,n 为正整数
∴解为
2 m+3 n=8
m=1
n=2
m·90 +n·135 =360
。
。
。
设在一个顶点周围有个 m 正四边形的角,n 个正八边形
的角,则有
∵ m,n 为正整数
∴解为
设在一个顶点周围有 m 个正五边形的角,n 个正十边形的角,则有
3 m+4 n=10
m=2
n=1
m·108 +n·144 =360
。
。
。
∵ m,n 为正整数
∴解为
用三种正多边形镶嵌,哪些能
镶嵌成一个平面?
探究问题(三)
思考同一种任意三角形可否镶嵌成一个平面?
同一种任意四边形可否镶嵌成一个平面?
收 集 整 理 数 据 正n边形 拼图 每个内角的度数 使用正多边形的个数k 结论
能镶嵌
能镶嵌
不能镶嵌
不能镶嵌
能镶嵌
K= 6
K= 4
K= 3
K= 4
K= 3
60°
90°
108°
108°
120°
n =3
n =6
n =4
n =5
分 析 数 据 正n边形 拼图 每个内角的度数
与360°的关系 结论
n=3
n=4
n=5
n=6
能镶嵌
不能镶嵌
不能镶嵌
能镶嵌
6×60°= 360°
4×90°= 360°
4×108°> 360°
3×120°= 360°
3×108°< 360°
能镶嵌
练习题
1.能够用一种正多边形铺满地面的是____。
A 正五边形 B 正六边形
C 正七边形 D 正八边形
2.如果用正三角形进行镶嵌,那么在每个顶 点的周围有____个正三角形。
3.如果用正三角形和正六边形进行镶嵌,那 么在每个顶点的周围有____ 个正三角形和____个正六边形或 ____个正三角形和____ 个正六边形
B
6
2
2
4
1
1. 用一种正多边形镶嵌,哪些可以,分别是哪些正多边形?
2. 你能找到用两种正多边形镶嵌,还有哪些吗?请你设计一个用两个正多边形镶嵌的图形。
课后作业:
谢谢!
