七年级数学数学: 3.1.2《线段、直线、射线-线段长短的比较》课件(湘教版七年级下)
文档属性
| 名称 | 七年级数学数学: 3.1.2《线段、直线、射线-线段长短的比较》课件(湘教版七年级下) |

|
|
| 格式 | zip | ||
| 文件大小 | 123.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-06-04 00:00:00 | ||
图片预览



文档简介
(共9张PPT)
义务教育课程标准实验教科书
SHUXUE 七年级下
在日常生活中,我们经常
要比较两条线段的长短,
为简单表示,我们把线段
AB的长也记作AB
两位同学要比较高矮,木工想量出黑板的长短,经常会采取什么办法呢?
把AB和CD都放到同一条直线上,使AB的一个端点A和CD的一个端点C重合,另一个端点B和D落在A和C的同侧,然后根据D点的位置来比较AB和CD:
如果D落在线段AB的延长线上,就说AB小于CD,记住AB如果B与D重合,就说AB等于CD,记住AB=CD;
如果D落在线段AB内,就说AB大于CD,记作AB>CD;
A
B
C
D
比较两条线段AB和CD长短的方法是:
A
B
C
D
A
B
C
D
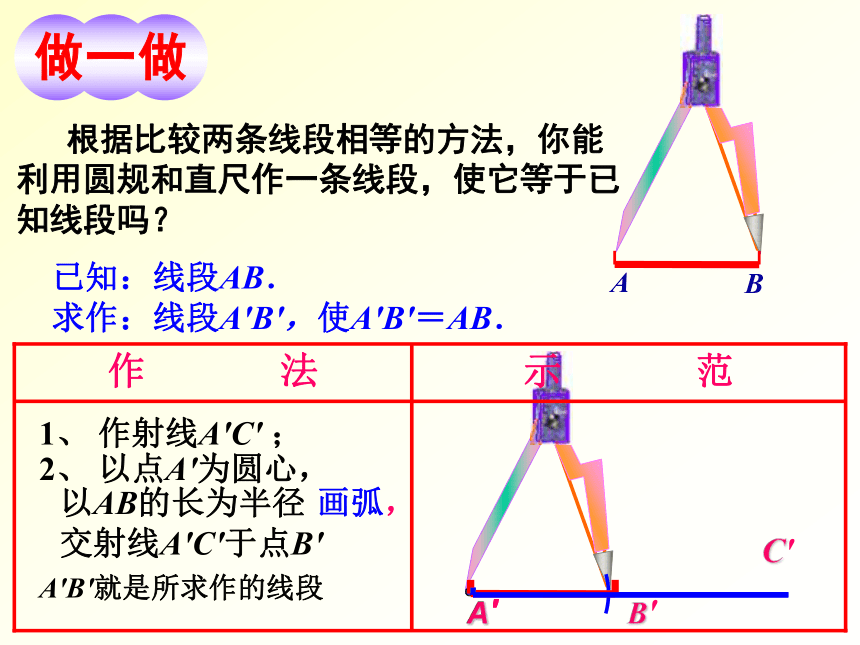
1、 作射线A′C′ ;
2、 以点A′为圆心,
以AB的长为半径
画弧,
交射线A′C′于点B′
A′
B′
A′B′就是所求作的线段
示 范
作 法
A
B
已知:线段AB.
求作:线段A′B′,使A′B′=AB.
C′
A′
根据比较两条线段相等的方法,你能利用圆规和直尺作一条线段,使它等于已知线段吗?
埃及的塞得港和苏伊士城的直线距离只有一百多千米,但是一片陆地不能行船,轮船必须绕道好望角到苏伊士城,后来人们开挖了苏伊士运河,使轮船航行路程缩短了几千千米,这是根据什么原理?
在广阔的原野上,旅行者要从A点走到B点,常常会走什么路线?
走直线路
连结两点的线段的长度,叫做这两点的距离.
A
B
人们根据长期实践经验得出:
连结两点的所有连线中,线段最短
a
已知线段a,作一条线段使它等于2a作法:
在图中B点在线段AC上,而且AB=BC,这时B点叫做线段AC的中点
则AC就是要作的线段
(1)作射线AD;
(2)在AD上相继取B点、C点,使得AB=BC=a
A
B
C
D
a
a
已知线段 a,b(a>b),作一条线段使它等于a-b
则线段AB就是求作的线段.
b
B
C
A
F
a
(1)作射线AF;
(2)在射线AF上,截取AC=a
(3)在线段CA上,截取CD=b,
作法:
a
b
任意画一条线段AB,再想办法找出它的中点M
折叠纸片,使这条线段的两个端点重合在一起,那么折痕与线段的交点就是线段的中点.
1.举出两个例子说明“连结两点的所有连线中,线段最短”这一性质在实际生活中的应用.
AB_____CD; OA_____BC; OA_____OC;
AB_____AD; AD_____BC;
O是线段__________和__________的中点.
B
C
A
D
2.量出图中线段AB,BC,CD,AD,OA,OC的长度,然后用“=、>、<”填空:
修公路取直凿隧道等
=
=
=
<
<
AC
BD
义务教育课程标准实验教科书
SHUXUE 七年级下
在日常生活中,我们经常
要比较两条线段的长短,
为简单表示,我们把线段
AB的长也记作AB
两位同学要比较高矮,木工想量出黑板的长短,经常会采取什么办法呢?
把AB和CD都放到同一条直线上,使AB的一个端点A和CD的一个端点C重合,另一个端点B和D落在A和C的同侧,然后根据D点的位置来比较AB和CD:
如果D落在线段AB的延长线上,就说AB小于CD,记住AB
如果D落在线段AB内,就说AB大于CD,记作AB>CD;
A
B
C
D
比较两条线段AB和CD长短的方法是:
A
B
C
D
A
B
C
D
1、 作射线A′C′ ;
2、 以点A′为圆心,
以AB的长为半径
画弧,
交射线A′C′于点B′
A′
B′
A′B′就是所求作的线段
示 范
作 法
A
B
已知:线段AB.
求作:线段A′B′,使A′B′=AB.
C′
A′
根据比较两条线段相等的方法,你能利用圆规和直尺作一条线段,使它等于已知线段吗?
埃及的塞得港和苏伊士城的直线距离只有一百多千米,但是一片陆地不能行船,轮船必须绕道好望角到苏伊士城,后来人们开挖了苏伊士运河,使轮船航行路程缩短了几千千米,这是根据什么原理?
在广阔的原野上,旅行者要从A点走到B点,常常会走什么路线?
走直线路
连结两点的线段的长度,叫做这两点的距离.
A
B
人们根据长期实践经验得出:
连结两点的所有连线中,线段最短
a
已知线段a,作一条线段使它等于2a作法:
在图中B点在线段AC上,而且AB=BC,这时B点叫做线段AC的中点
则AC就是要作的线段
(1)作射线AD;
(2)在AD上相继取B点、C点,使得AB=BC=a
A
B
C
D
a
a
已知线段 a,b(a>b),作一条线段使它等于a-b
则线段AB就是求作的线段.
b
B
C
A
F
a
(1)作射线AF;
(2)在射线AF上,截取AC=a
(3)在线段CA上,截取CD=b,
作法:
a
b
任意画一条线段AB,再想办法找出它的中点M
折叠纸片,使这条线段的两个端点重合在一起,那么折痕与线段的交点就是线段的中点.
1.举出两个例子说明“连结两点的所有连线中,线段最短”这一性质在实际生活中的应用.
AB_____CD; OA_____BC; OA_____OC;
AB_____AD; AD_____BC;
O是线段__________和__________的中点.
B
C
A
D
2.量出图中线段AB,BC,CD,AD,OA,OC的长度,然后用“=、>、<”填空:
修公路取直凿隧道等
=
=
=
<
<
AC
BD
