4.7.2 相似三角形的性质2 课件(共17张PPT)
文档属性
| 名称 | 4.7.2 相似三角形的性质2 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-19 08:55:24 | ||
图片预览






文档简介
(共17张PPT)
北师大版
九年级上
第四章
图形的相似
第二课时
4.7
相似三角形的性质
学
习
目
标
1.理解并熟练应用相似三角形的性质:周长比等于相似比,面积比等于相似比的平方.(重点)
2.会利用相似三角形的性质来解决简单的问题.(难点)
两个相似三角形的_______相等,_______成比例.
对应角
对应边
相似三角形对应高的比
_________________________、
____________________________、
________________________________都等于相似比.
相似三角形对应中线的比
相似三角形对应角平分线的比
相似三角形的性质:
知识回顾
1.如图所示的两个三角形相似吗?相似比是多少?周长比是多少?面积比是多少?
合作探究
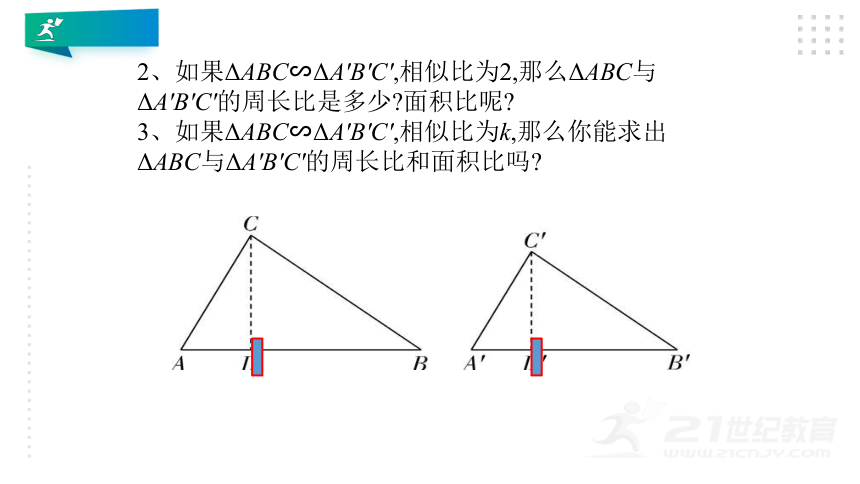
2、如果ΔABC∽ΔA'B'C',相似比为2,那么ΔABC与ΔA'B'C'的周长比是多少?面积比呢?
3、如果ΔABC∽ΔA'B'C',相似比为k,那么你能求出ΔABC与ΔA'B'C'的周长比和面积比吗?
∽
定理
(1)相似三角形的周长比等于相似比。
(2)相似三角形的面积比等于相似比的平方.
知识总结
1.已知ΔABC与ΔA′B′C′的相似比为2:3,则对
应边上中线之比
,面积之比为
.
2.
如果两个相似三角形的面积之比为1:9,
周长的比为______
.
1:3
2:3
4:9
随堂训练
例1:将△ABC沿BC方向平移得到△DEF,△ABC与△DEF重叠部分的面积是△ABC的面积的一半.已知BC=2,求△ABC平移的距离.
解:根据题意,可知EG∥AB.
∴∠GEC=∠B,∠EGC=∠A.
∴△GEC∽△ABC
即,△ABC平移的距离为
例题讲解
例2:如图所示,D、E分别是AC、AB上的点,已知△ABC的面积为100cm2
,且
求四边形BCDE的面积.
∴△ABC
∽△ADE
.
∴它们的相似比为5:3,面积比为25:9.
又∵△ABC的面积为100
cm2
,
∴△ADE的面积为36
cm2
.
∴四边形BCDE的面积为100-36=64(
cm2
)
.
解:∵∠BAD=∠DAE,且
B
A
E
D
C
相似三角形的性质2
相似三角形周长之比等于相似比
相似三角形面积之比等于相似比的平方
课堂小结
1.连结三角形两边中点的线段把三角形截成的一个小三角形与原三角形的周长比等于______,面积比等于_______.
2.两个相似三角形对应的中线长分别是6cm和18cm,若较大三角形的周长是42cm,面积是12cm2,则较小三角形的周长____cm,面积为____cm2.
1:2
1:4
14
当堂检测
3.判断:
(1)一个三角形的各边长扩大为原来的5倍,这个三角形的周长也扩大为原来的5倍.(
)
(2)一个四边形的各边长扩大为原来的9倍,这个四边形的面积也扩大为原来的9倍.(
)
√
×
4.如图,
ABCD中,E为AD的中点,若
S
ABCD=1,则图中阴影部分的面积为
(
)
A.
B.
C.
D.
B
A
E
D
C
F
B
5.
若△ABC
∽△
A′B′C′
,它们的周长分别为60cm和72cm,且AB=15cm,B′C′=24cm,求BC,AC,A′B′,A′C′的长.
B
A
C
解:∵
△ABC
∽△
A′B′C′
,它们的周长分别为60cm和72cm,
∵AB=15cm,B′C′=24cm,
∴BC
=
20cm,
AC
=
25cm,
A′B′=18cm,A′C′=30cm.
https://www.21cnjy.com/help/help_extract.php
北师大版
九年级上
第四章
图形的相似
第二课时
4.7
相似三角形的性质
学
习
目
标
1.理解并熟练应用相似三角形的性质:周长比等于相似比,面积比等于相似比的平方.(重点)
2.会利用相似三角形的性质来解决简单的问题.(难点)
两个相似三角形的_______相等,_______成比例.
对应角
对应边
相似三角形对应高的比
_________________________、
____________________________、
________________________________都等于相似比.
相似三角形对应中线的比
相似三角形对应角平分线的比
相似三角形的性质:
知识回顾
1.如图所示的两个三角形相似吗?相似比是多少?周长比是多少?面积比是多少?
合作探究
2、如果ΔABC∽ΔA'B'C',相似比为2,那么ΔABC与ΔA'B'C'的周长比是多少?面积比呢?
3、如果ΔABC∽ΔA'B'C',相似比为k,那么你能求出ΔABC与ΔA'B'C'的周长比和面积比吗?
∽
定理
(1)相似三角形的周长比等于相似比。
(2)相似三角形的面积比等于相似比的平方.
知识总结
1.已知ΔABC与ΔA′B′C′的相似比为2:3,则对
应边上中线之比
,面积之比为
.
2.
如果两个相似三角形的面积之比为1:9,
周长的比为______
.
1:3
2:3
4:9
随堂训练
例1:将△ABC沿BC方向平移得到△DEF,△ABC与△DEF重叠部分的面积是△ABC的面积的一半.已知BC=2,求△ABC平移的距离.
解:根据题意,可知EG∥AB.
∴∠GEC=∠B,∠EGC=∠A.
∴△GEC∽△ABC
即,△ABC平移的距离为
例题讲解
例2:如图所示,D、E分别是AC、AB上的点,已知△ABC的面积为100cm2
,且
求四边形BCDE的面积.
∴△ABC
∽△ADE
.
∴它们的相似比为5:3,面积比为25:9.
又∵△ABC的面积为100
cm2
,
∴△ADE的面积为36
cm2
.
∴四边形BCDE的面积为100-36=64(
cm2
)
.
解:∵∠BAD=∠DAE,且
B
A
E
D
C
相似三角形的性质2
相似三角形周长之比等于相似比
相似三角形面积之比等于相似比的平方
课堂小结
1.连结三角形两边中点的线段把三角形截成的一个小三角形与原三角形的周长比等于______,面积比等于_______.
2.两个相似三角形对应的中线长分别是6cm和18cm,若较大三角形的周长是42cm,面积是12cm2,则较小三角形的周长____cm,面积为____cm2.
1:2
1:4
14
当堂检测
3.判断:
(1)一个三角形的各边长扩大为原来的5倍,这个三角形的周长也扩大为原来的5倍.(
)
(2)一个四边形的各边长扩大为原来的9倍,这个四边形的面积也扩大为原来的9倍.(
)
√
×
4.如图,
ABCD中,E为AD的中点,若
S
ABCD=1,则图中阴影部分的面积为
(
)
A.
B.
C.
D.
B
A
E
D
C
F
B
5.
若△ABC
∽△
A′B′C′
,它们的周长分别为60cm和72cm,且AB=15cm,B′C′=24cm,求BC,AC,A′B′,A′C′的长.
B
A
C
解:∵
△ABC
∽△
A′B′C′
,它们的周长分别为60cm和72cm,
∵AB=15cm,B′C′=24cm,
∴BC
=
20cm,
AC
=
25cm,
A′B′=18cm,A′C′=30cm.
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
