4.8.1 位似图形及其画法 课件(共19张PPT)
文档属性
| 名称 | 4.8.1 位似图形及其画法 课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-19 08:56:33 | ||
图片预览



文档简介
(共19张PPT)
北师大版
九年级上
第四章
图形的相似
第一课时
位似图形及其画法
4.8
图形的位似
学
习
目
标
1.
了解图形位似的定义和相关性质;(重点)
2.
理解相似多边形与位似多边形的联系与区别;(重点)
3.
初步掌握利用位似把多边形按照一定比例放大或缩小的绘图方法。(难点)
九年级(1)班的同学们筹备一次班会,为了活跃气氛,他们想把下面两个图样放大,使放大前后对应线段的比为1︰2,然后制成各种彩纸图片,请你帮助他们找到放大图样的方法。
下面我们就一起来学习一种把图形放大或缩小的方法。
新课导入
知识讲解
位似图形的定义
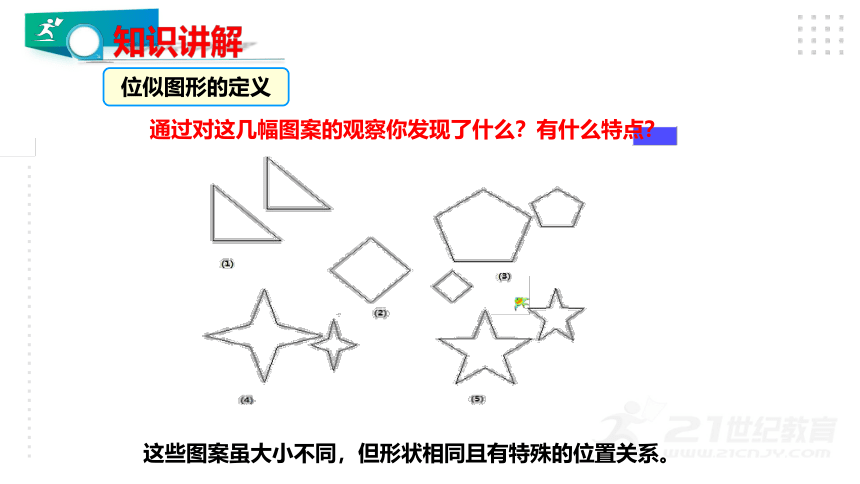
通过对这几幅图案的观察你发现了什么?有什么特点?
这些图案虽大小不同,但形状相同且有特殊的位置关系。
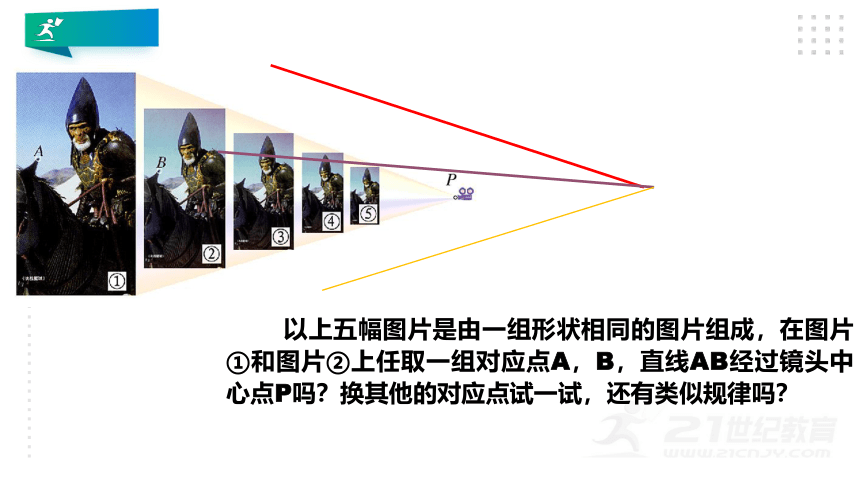
以上五幅图片是由一组形状相同的图片组成,在图片①和图片②上任取一组对应点A,B,直线AB经过镜头中心点P吗?换其他的对应点试一试,还有类似规律吗?
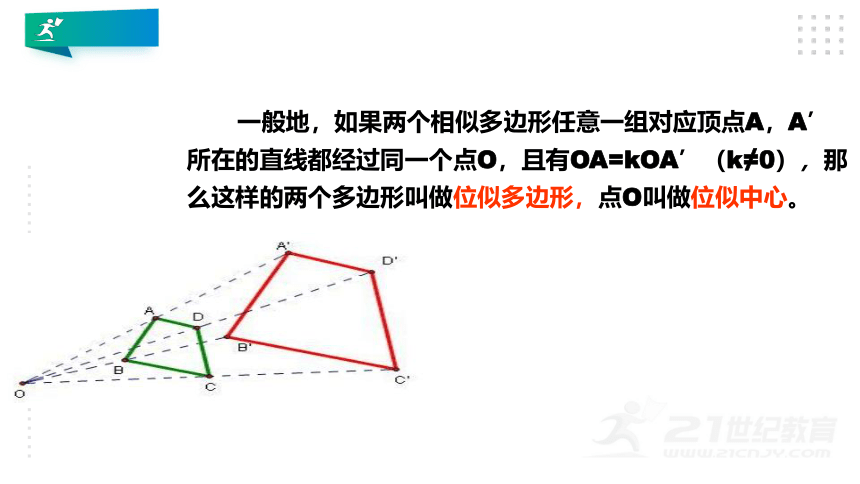
一般地,如果两个相似多边形任意一组对应顶点A,A’所在的直线都经过同一个点O,且有OA=kOA’(k≠0),那么这样的两个多边形叫做位似多边形,点O叫做位似中心。
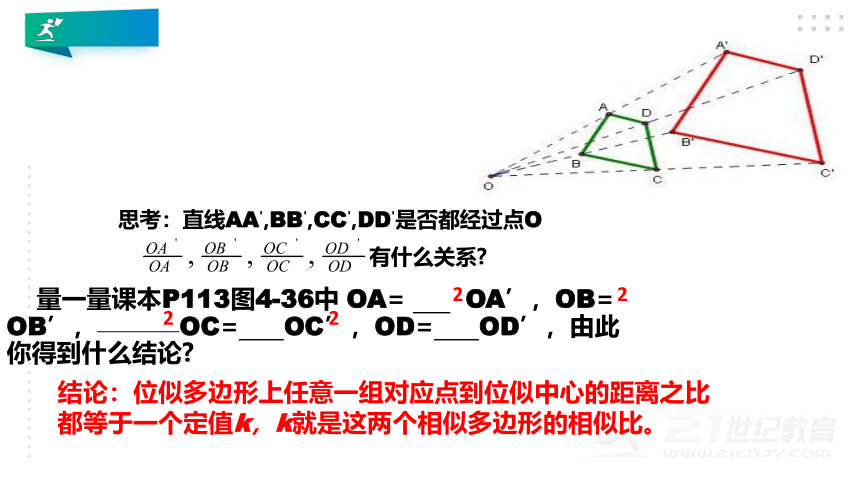
量一量课本P113图4-36中
OA=
OA’,OB=
OB’,
OC=
OC’,OD=
OD’,由此你得到什么结论?
有什么关系?
结论:位似多边形上任意一组对应点到位似中心的距离之比都等于一个定值k,k就是这两个相似多边形的相似比。
思考:直线AA',BB',CC',DD'是否都经过点O
2
2
2
2
1.
以下每组位似图形中的位似中心在哪里?
2.
两个位似的图形具有什么特征?
图(2)(3)(5)中对应点在位似中心的同侧,
图(1)(4)(6)中对应点在位似中心的异侧。
位似图形的性质
归纳总结
5.
位似多边形是具有特殊位置关系的相似多边形。
1.
位似图形的对应线段有可能平行,也有可能共线.
2.
两图形可能出现在位似中心的同侧或者异侧.
3.
位似中心可能位于两个图形的内部,也可能在两图形的公共顶点上,还可能在两个图形的外部.
4.
每一组对应点到位似中心的距离之比都等于相似比.
例1:如图,已知△ABC,以点O为位似中心画△DEF,使其与△ABC位似,且位似比为2.
解:画射线OA,OB,OC;在射线OA,OB,OC上分别取点D,E,F,使OD
=
2OA,OE
=
2OB,OF
=
2OC;顺序连接D,E,F,使△DEF与△ABC位似,相似比为2.
A
B
C
F
E
D
O
想一想:你还有其他的画法吗?
位似图形的画法
A
B
C
画法二:△ABC与△DEF异侧
解:画射线OA,OB,OC;沿着射线OA,OB,OC反方向上分别取点D,E,F,OD
=
2OA,OE
=
2OB,OF
=
2OC;顺序连接D,E,F,使△DEF与△ABC位似,相似比为2.
O
E
F
D
下列关于位似图形的表述:
1.
相似图形一定是位似图形,位似图形一定是相似图形;
2.
位似图形一定有位似中心;
3.
如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,那么,这两个图形是位似图形;
4.
位似图形上任意两点与位似中心的距离之比等于位似比.
其中正确命题的序号是( )
A.②③
B.①②
C.③④
D.②③④
A
随堂训练
用以下方法可以近似地把一个图形放大:
1.
将两根长短相同的橡皮筋系在一起,联接处形成一个结点
;
2.
选一个图形,在图形外取一个定点
;
4.
拉动铅笔,使结点沿所选图形的边缘运动,当结点在已知图形上运动一圈时,铅笔就画出一个新的图形。
3.
将系在一起的橡皮筋的一端固定在定点,把铅笔固定在橡皮筋的另一端
;
拓展延伸
位似图形
定义
性质:位似图形上对应点到位似中心的距
离之比等于相似比
课堂小结
画位似图形的步骤
确定位似中心
画出两位似图形对应点到位似中心的相似比的线段
顺次连接位似图形的各点
1.如图,A′B′∥AB,B′C′∥BC,且OA′∶A′A=
4∶3,则△ABC与
是位似图形,位似比为
;△OAB与
是位似图形,位似比为
.
2.如图,图中两个四边形是位似图形,它们的位似中心是(
)
A.点M
B.点N
C.点O
D.点P
第1题图
第2题图
△A′B′C′
7∶4
△OA′B′
7∶4
D
当堂检测
3.下列相似图形是否是位似图形?如果是请指出位似中心,如果不是请说明理由。
B
A
C
E
D
F
E
D
C
B
A
H
G
4.
判断下列各对图形是不是位似图形.
(1)正五边形ABCDE与正五边形A′B′C′D′E′;
(2)等边三角形ABC与等边三角形A′B′C′.
是
是
5.若△ABC与△A’B’C’的相似比为:1:2,
则OA:OA’=
.
O
A
A’
B
C
B’
C’
1:2
https://www.21cnjy.com/help/help_extract.php
北师大版
九年级上
第四章
图形的相似
第一课时
位似图形及其画法
4.8
图形的位似
学
习
目
标
1.
了解图形位似的定义和相关性质;(重点)
2.
理解相似多边形与位似多边形的联系与区别;(重点)
3.
初步掌握利用位似把多边形按照一定比例放大或缩小的绘图方法。(难点)
九年级(1)班的同学们筹备一次班会,为了活跃气氛,他们想把下面两个图样放大,使放大前后对应线段的比为1︰2,然后制成各种彩纸图片,请你帮助他们找到放大图样的方法。
下面我们就一起来学习一种把图形放大或缩小的方法。
新课导入
知识讲解
位似图形的定义
通过对这几幅图案的观察你发现了什么?有什么特点?
这些图案虽大小不同,但形状相同且有特殊的位置关系。
以上五幅图片是由一组形状相同的图片组成,在图片①和图片②上任取一组对应点A,B,直线AB经过镜头中心点P吗?换其他的对应点试一试,还有类似规律吗?
一般地,如果两个相似多边形任意一组对应顶点A,A’所在的直线都经过同一个点O,且有OA=kOA’(k≠0),那么这样的两个多边形叫做位似多边形,点O叫做位似中心。
量一量课本P113图4-36中
OA=
OA’,OB=
OB’,
OC=
OC’,OD=
OD’,由此你得到什么结论?
有什么关系?
结论:位似多边形上任意一组对应点到位似中心的距离之比都等于一个定值k,k就是这两个相似多边形的相似比。
思考:直线AA',BB',CC',DD'是否都经过点O
2
2
2
2
1.
以下每组位似图形中的位似中心在哪里?
2.
两个位似的图形具有什么特征?
图(2)(3)(5)中对应点在位似中心的同侧,
图(1)(4)(6)中对应点在位似中心的异侧。
位似图形的性质
归纳总结
5.
位似多边形是具有特殊位置关系的相似多边形。
1.
位似图形的对应线段有可能平行,也有可能共线.
2.
两图形可能出现在位似中心的同侧或者异侧.
3.
位似中心可能位于两个图形的内部,也可能在两图形的公共顶点上,还可能在两个图形的外部.
4.
每一组对应点到位似中心的距离之比都等于相似比.
例1:如图,已知△ABC,以点O为位似中心画△DEF,使其与△ABC位似,且位似比为2.
解:画射线OA,OB,OC;在射线OA,OB,OC上分别取点D,E,F,使OD
=
2OA,OE
=
2OB,OF
=
2OC;顺序连接D,E,F,使△DEF与△ABC位似,相似比为2.
A
B
C
F
E
D
O
想一想:你还有其他的画法吗?
位似图形的画法
A
B
C
画法二:△ABC与△DEF异侧
解:画射线OA,OB,OC;沿着射线OA,OB,OC反方向上分别取点D,E,F,OD
=
2OA,OE
=
2OB,OF
=
2OC;顺序连接D,E,F,使△DEF与△ABC位似,相似比为2.
O
E
F
D
下列关于位似图形的表述:
1.
相似图形一定是位似图形,位似图形一定是相似图形;
2.
位似图形一定有位似中心;
3.
如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,那么,这两个图形是位似图形;
4.
位似图形上任意两点与位似中心的距离之比等于位似比.
其中正确命题的序号是( )
A.②③
B.①②
C.③④
D.②③④
A
随堂训练
用以下方法可以近似地把一个图形放大:
1.
将两根长短相同的橡皮筋系在一起,联接处形成一个结点
;
2.
选一个图形,在图形外取一个定点
;
4.
拉动铅笔,使结点沿所选图形的边缘运动,当结点在已知图形上运动一圈时,铅笔就画出一个新的图形。
3.
将系在一起的橡皮筋的一端固定在定点,把铅笔固定在橡皮筋的另一端
;
拓展延伸
位似图形
定义
性质:位似图形上对应点到位似中心的距
离之比等于相似比
课堂小结
画位似图形的步骤
确定位似中心
画出两位似图形对应点到位似中心的相似比的线段
顺次连接位似图形的各点
1.如图,A′B′∥AB,B′C′∥BC,且OA′∶A′A=
4∶3,则△ABC与
是位似图形,位似比为
;△OAB与
是位似图形,位似比为
.
2.如图,图中两个四边形是位似图形,它们的位似中心是(
)
A.点M
B.点N
C.点O
D.点P
第1题图
第2题图
△A′B′C′
7∶4
△OA′B′
7∶4
D
当堂检测
3.下列相似图形是否是位似图形?如果是请指出位似中心,如果不是请说明理由。
B
A
C
E
D
F
E
D
C
B
A
H
G
4.
判断下列各对图形是不是位似图形.
(1)正五边形ABCDE与正五边形A′B′C′D′E′;
(2)等边三角形ABC与等边三角形A′B′C′.
是
是
5.若△ABC与△A’B’C’的相似比为:1:2,
则OA:OA’=
.
O
A
A’
B
C
B’
C’
1:2
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
