4.3 相似多边形 课件(共29张PPT)
文档属性
| 名称 | 4.3 相似多边形 课件(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-19 08:43:31 | ||
图片预览



文档简介
(共29张PPT)
北师大版
九年级上
第四章
图形的相似
4.3相似多边形
学
习
目
标
1.了解相似多边形和相似比的概念.
2.会根据条件判断两个多边形是否为相似多边形.(重点)
3.掌握相似多边形的性质,能根据相似比进行相关的计算.(难点)
B
C
A
D
E
F
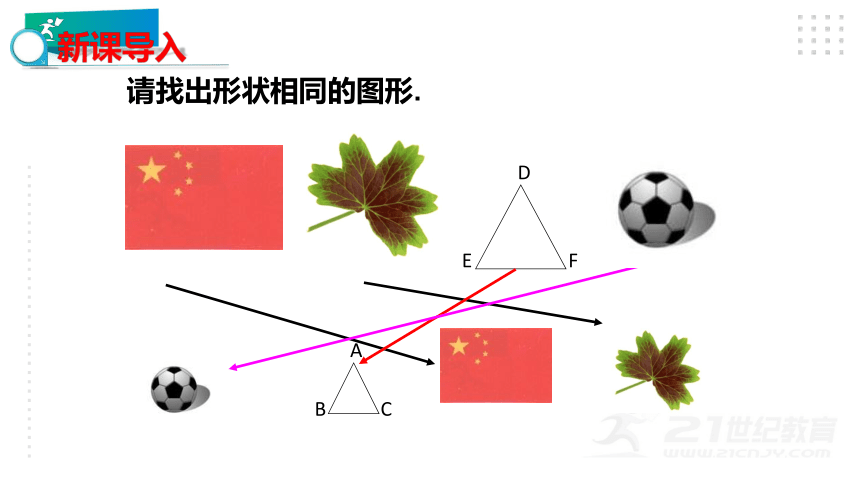
请找出形状相同的图形.
新课导入
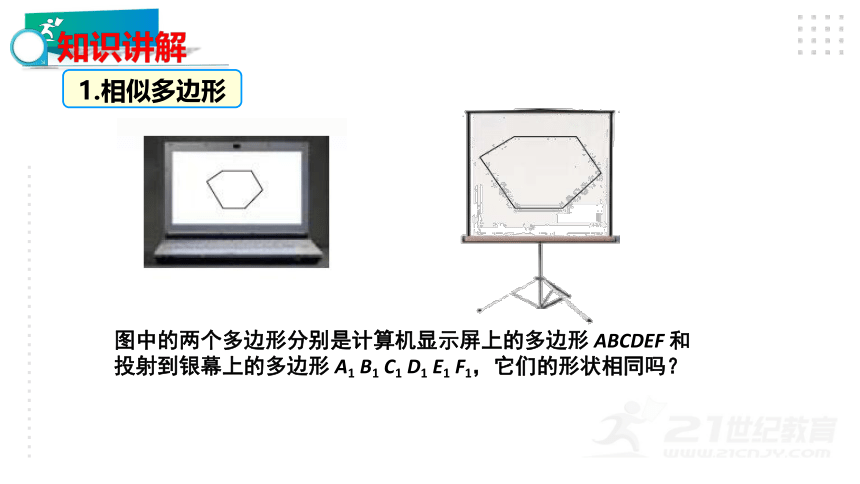
图中的两个多边形分别是计算机显示屏上的多边形
ABCDEF
和投射到银幕上的多边形
A1
B1
C1
D1
E1
F1,它们的形状相同吗?
知识讲解
1.相似多边形
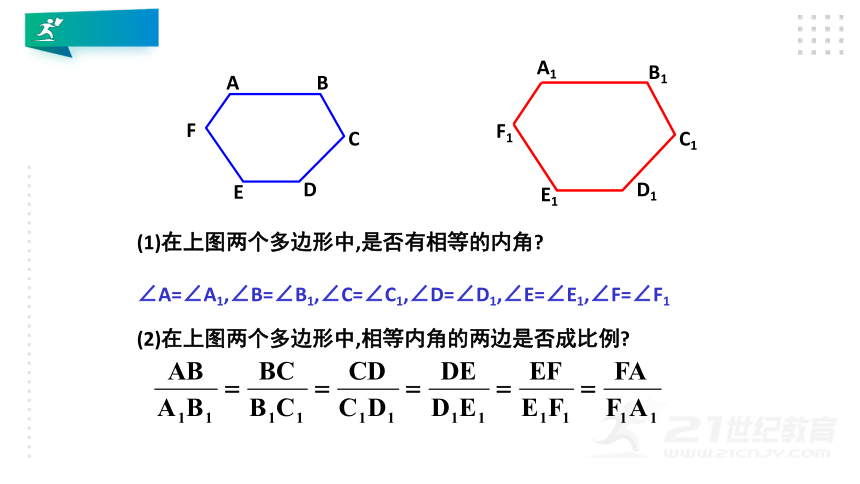
(1)在上图两个多边形中,是否有相等的内角?
(2)在上图两个多边形中,相等内角的两边是否成比例?
∠A=∠A1,∠B=∠B1,∠C=∠C1,∠D=∠D1,∠E=∠E1,∠F=∠F1
A
B
C
D
E
F
A1
B1
C1
D1
E1
F1
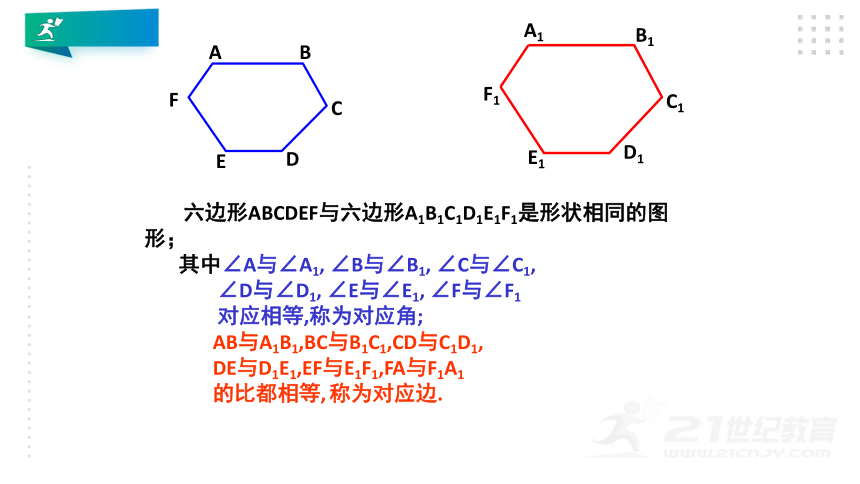
六边形ABCDEF与六边形A1B1C1D1E1F1是形状相同的图形;
其中∠A与∠A1,
∠B与∠B1,
∠C与∠C1,
∠D与∠D1,
∠E与∠E1,
∠F与∠F1
对应相等,称为对应角;
AB与A1B1,BC与B1C1,CD与C1D1,
DE与D1E1,EF与E1F1,FA与F1A1
的比都相等,
称为对应边.
A
B
C
D
E
F
A1
B1
C1
D1
E1
F1
相似多边形概念:
各角分别相等、各边成比例的两个多边形叫做相似多边形。
如:六边形ABCDEF与六边形A1B1C1D1E1F1相似,
记作六边形ABCDEF
∽六边形A1B1C1D1E1F1,
2、在记两个多边形相似时,要把表示对应角顶点的字母写在对应的位置上。
注:1、相似符号“∽
”读作“相似于”
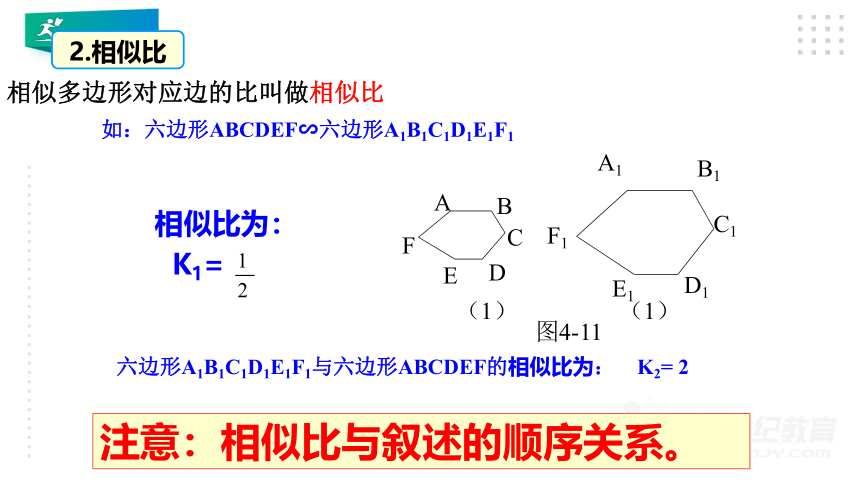
相似多边形对应边的比叫做相似比
注意:相似比与叙述的顺序关系。
(1)
B
C
D
E
F
A
B1
C1
D1
E1
F1
A1
(1)
图4-11
如:六边形ABCDEF∽六边形A1B1C1D1E1F1
六边形A1B1C1D1E1F1与六边形ABCDEF的相似比为:
K2=
2
相似比为:
K1=
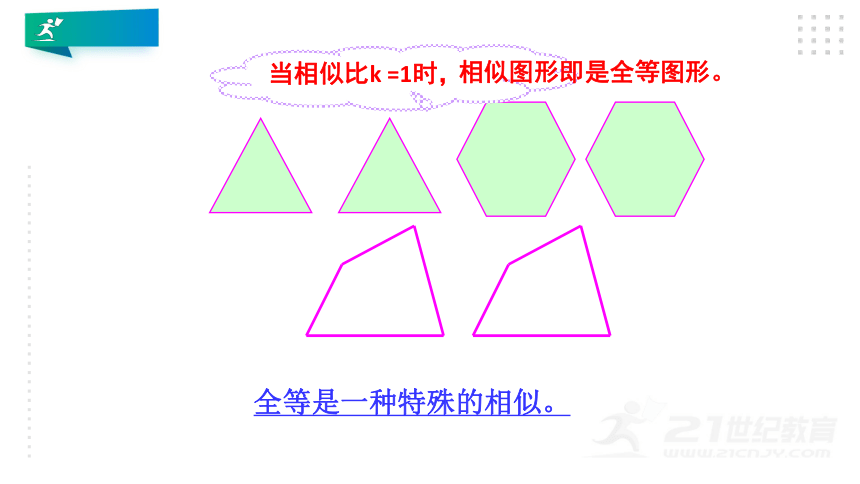
2.相似比
全等是一种特殊的相似。
当相似比k
=1时,
相似图形即是全等图形。
A
B
C
F
E
D
A1
B1
C1
F1
E1
D1
六边形ABCDEF与六边形A1B1C1D1E1F1的相似比为
k1=
2
:
1,
对应边
AB:A1B1=
2
:
1
。
A1
B1
C1
F1
E1
D1
A
B
C
F
E
D
六边形ABCDEF与六边形A1B1C1D1E1F1的相似比为
k2=
1
:
2,
对应边
AB:A1B1=
1
:
2
。
相似比与叙述的顺序有关。
例
1.
下列每组图形形状相同,它们的对应角有怎样的关系?对应边呢?
(1)正三角形ABC与正三角形DEF
(1)由于正三角形每个角等于
,
所以
由于正三角形三边相等,
所以
解:
A
B
C
D
E
F
(2)正方形ABCD与正方形EFGH
(2)由于正方形的每个角都是直角,
所以
由于正方形四边相等,
所以
解:
A
B
D
C
E
F
G
H
正六边形
放大
(1)对应角有什么关系?
135°
135°
∠A
=∠A1,
∠B
=∠B1,
∠C
=∠C1
对应角相等
A
B
C
A1
B1
C1
F
E
D
F1
E1
D1
∠D
=∠D1,
∠E
=∠E1,
∠F
=∠F1
3.相似多边形的性质
正六边形
放大
(2)对应边有什么关系?
A
B
C
A1
B1
C1
F
E
D
F1
E1
D1
AB
=
BC
=
CD
=
DE
=
EF
=
FA
,
A1B1
=
B1C1
=
C1D1
=
D1E1
=
E1F1
=
F1A1
对应边成比例
A1B1
AB
B1C1
BC
=
C1D1
CD
D1E1
DE
=
E1F1
EF
F1A1
FA
=
=
=
(3)任意两个菱形相似吗?
对应边成比例,但对应角不一定相等。
任意两个菱形不一定相似。
1.如果两个多边形相似,那么它们的对应角有什么关系?
对应边呢?
答:如果两个多边形相似,它们的对应角都相等,对应边成比例。
合作探究
如果两个多边形不相似,那么它们的对应角可能都相等吗?
对应边可能都成比例吗?
答:如果两个多边形不相似,它们的对应角可能都相等;如果两个多边形不相似,对应边也可能成比例。
但如果两个多边形不相似,那么它们不可能各角对应相等且各边对应成比例.
一块长3m、宽1.5m的矩形黑板如下图所示,镶在其外围的木质边框宽7.5cm。边框的内外边缘所成的矩形相似吗?为什么?
3m
1.5m
A
B
C
D
E
F
G
H
(3+0.075×2)m
(1.5+0.075×2)m
直观有时是不可靠的
1.5︰3≠1.65︰3.15
做一做
例1.
判断两个多边形是否相似
3
正方形
3
4
4
菱形
解:
∵
正方形,菱形的四条边都相等.
∴
它们的对应边成比例,k
=
3
:
4.
∵
正方形的四个内角均为直角,而菱形的内角有钝角有锐角.
∴
它们的对应角不相等.
∴
这一组图形不相似.
例题讲解
3
正方形
3
6
8
长方形
解:∵
正方形和矩形的四个内角都是直角.
∴
它们的对应角相等.
∵
对应边
3
:
6
≠
3
:
8.
∴
它们的对应边不成比例.
∴
这一组图形不相似.
1、判断:
(1)任意两个矩形都是相似图形(
)
(2)任意两个圆形是相似图形(
)
(3)对应角相等的两个四边形是相似多边形(
)
(4)两个正五边形是相似多边形(
)
(5)两个全等三角形是相似多边形(
)
(6)两菱形是相似多边形(
)
(7)两个相似多边形,对应边成比例(
)
√
√
√
×
√
×
×
随堂训练
2、五边形ABCDE∽五边形
A?B?C?D?E?,则
∠
E=____,∠
A?=____,
C?D?=____
五边形A?B?C?D?E?与五边形ABCDE的相似比为_____.
118°
A
E
D
C
B
3
2
6
80°
A?
E?
D?
C?
B?
E
F
G
H
.
80°
118°
4
2:1
定义:各角分别相等、各边成比例的两个多边形叫做
相似多边形.
性质:相似多边形的对应角相等,对应边成比例.
相似比:相似多边形对应边的比叫做相似比.
课堂小结
1.下列命题中,正确的是(
)
A.所有的等腰三角形都相似
B.所有的直角三角形都相似
C.所有的等边三角形都相似
D.所有的矩形都相似
C
当堂检测
2、若△ABC∽△
A′B′C′,且AB:A′B′=1:2
则△ABC与△
A′B′C′相似比是
,
△
A′B′C′与△ABC的相似比是 .
2
解:
∵
△
ADE
∽△
ABC,
3.已知△ADE∽△ABC,点A、D、E分别与点
A、B、C对应,且相似比为
,若DE=
4cm,
求BC的长.
https://www.21cnjy.com/help/help_extract.php
北师大版
九年级上
第四章
图形的相似
4.3相似多边形
学
习
目
标
1.了解相似多边形和相似比的概念.
2.会根据条件判断两个多边形是否为相似多边形.(重点)
3.掌握相似多边形的性质,能根据相似比进行相关的计算.(难点)
B
C
A
D
E
F
请找出形状相同的图形.
新课导入
图中的两个多边形分别是计算机显示屏上的多边形
ABCDEF
和投射到银幕上的多边形
A1
B1
C1
D1
E1
F1,它们的形状相同吗?
知识讲解
1.相似多边形
(1)在上图两个多边形中,是否有相等的内角?
(2)在上图两个多边形中,相等内角的两边是否成比例?
∠A=∠A1,∠B=∠B1,∠C=∠C1,∠D=∠D1,∠E=∠E1,∠F=∠F1
A
B
C
D
E
F
A1
B1
C1
D1
E1
F1
六边形ABCDEF与六边形A1B1C1D1E1F1是形状相同的图形;
其中∠A与∠A1,
∠B与∠B1,
∠C与∠C1,
∠D与∠D1,
∠E与∠E1,
∠F与∠F1
对应相等,称为对应角;
AB与A1B1,BC与B1C1,CD与C1D1,
DE与D1E1,EF与E1F1,FA与F1A1
的比都相等,
称为对应边.
A
B
C
D
E
F
A1
B1
C1
D1
E1
F1
相似多边形概念:
各角分别相等、各边成比例的两个多边形叫做相似多边形。
如:六边形ABCDEF与六边形A1B1C1D1E1F1相似,
记作六边形ABCDEF
∽六边形A1B1C1D1E1F1,
2、在记两个多边形相似时,要把表示对应角顶点的字母写在对应的位置上。
注:1、相似符号“∽
”读作“相似于”
相似多边形对应边的比叫做相似比
注意:相似比与叙述的顺序关系。
(1)
B
C
D
E
F
A
B1
C1
D1
E1
F1
A1
(1)
图4-11
如:六边形ABCDEF∽六边形A1B1C1D1E1F1
六边形A1B1C1D1E1F1与六边形ABCDEF的相似比为:
K2=
2
相似比为:
K1=
2.相似比
全等是一种特殊的相似。
当相似比k
=1时,
相似图形即是全等图形。
A
B
C
F
E
D
A1
B1
C1
F1
E1
D1
六边形ABCDEF与六边形A1B1C1D1E1F1的相似比为
k1=
2
:
1,
对应边
AB:A1B1=
2
:
1
。
A1
B1
C1
F1
E1
D1
A
B
C
F
E
D
六边形ABCDEF与六边形A1B1C1D1E1F1的相似比为
k2=
1
:
2,
对应边
AB:A1B1=
1
:
2
。
相似比与叙述的顺序有关。
例
1.
下列每组图形形状相同,它们的对应角有怎样的关系?对应边呢?
(1)正三角形ABC与正三角形DEF
(1)由于正三角形每个角等于
,
所以
由于正三角形三边相等,
所以
解:
A
B
C
D
E
F
(2)正方形ABCD与正方形EFGH
(2)由于正方形的每个角都是直角,
所以
由于正方形四边相等,
所以
解:
A
B
D
C
E
F
G
H
正六边形
放大
(1)对应角有什么关系?
135°
135°
∠A
=∠A1,
∠B
=∠B1,
∠C
=∠C1
对应角相等
A
B
C
A1
B1
C1
F
E
D
F1
E1
D1
∠D
=∠D1,
∠E
=∠E1,
∠F
=∠F1
3.相似多边形的性质
正六边形
放大
(2)对应边有什么关系?
A
B
C
A1
B1
C1
F
E
D
F1
E1
D1
AB
=
BC
=
CD
=
DE
=
EF
=
FA
,
A1B1
=
B1C1
=
C1D1
=
D1E1
=
E1F1
=
F1A1
对应边成比例
A1B1
AB
B1C1
BC
=
C1D1
CD
D1E1
DE
=
E1F1
EF
F1A1
FA
=
=
=
(3)任意两个菱形相似吗?
对应边成比例,但对应角不一定相等。
任意两个菱形不一定相似。
1.如果两个多边形相似,那么它们的对应角有什么关系?
对应边呢?
答:如果两个多边形相似,它们的对应角都相等,对应边成比例。
合作探究
如果两个多边形不相似,那么它们的对应角可能都相等吗?
对应边可能都成比例吗?
答:如果两个多边形不相似,它们的对应角可能都相等;如果两个多边形不相似,对应边也可能成比例。
但如果两个多边形不相似,那么它们不可能各角对应相等且各边对应成比例.
一块长3m、宽1.5m的矩形黑板如下图所示,镶在其外围的木质边框宽7.5cm。边框的内外边缘所成的矩形相似吗?为什么?
3m
1.5m
A
B
C
D
E
F
G
H
(3+0.075×2)m
(1.5+0.075×2)m
直观有时是不可靠的
1.5︰3≠1.65︰3.15
做一做
例1.
判断两个多边形是否相似
3
正方形
3
4
4
菱形
解:
∵
正方形,菱形的四条边都相等.
∴
它们的对应边成比例,k
=
3
:
4.
∵
正方形的四个内角均为直角,而菱形的内角有钝角有锐角.
∴
它们的对应角不相等.
∴
这一组图形不相似.
例题讲解
3
正方形
3
6
8
长方形
解:∵
正方形和矩形的四个内角都是直角.
∴
它们的对应角相等.
∵
对应边
3
:
6
≠
3
:
8.
∴
它们的对应边不成比例.
∴
这一组图形不相似.
1、判断:
(1)任意两个矩形都是相似图形(
)
(2)任意两个圆形是相似图形(
)
(3)对应角相等的两个四边形是相似多边形(
)
(4)两个正五边形是相似多边形(
)
(5)两个全等三角形是相似多边形(
)
(6)两菱形是相似多边形(
)
(7)两个相似多边形,对应边成比例(
)
√
√
√
×
√
×
×
随堂训练
2、五边形ABCDE∽五边形
A?B?C?D?E?,则
∠
E=____,∠
A?=____,
C?D?=____
五边形A?B?C?D?E?与五边形ABCDE的相似比为_____.
118°
A
E
D
C
B
3
2
6
80°
A?
E?
D?
C?
B?
E
F
G
H
.
80°
118°
4
2:1
定义:各角分别相等、各边成比例的两个多边形叫做
相似多边形.
性质:相似多边形的对应角相等,对应边成比例.
相似比:相似多边形对应边的比叫做相似比.
课堂小结
1.下列命题中,正确的是(
)
A.所有的等腰三角形都相似
B.所有的直角三角形都相似
C.所有的等边三角形都相似
D.所有的矩形都相似
C
当堂检测
2、若△ABC∽△
A′B′C′,且AB:A′B′=1:2
则△ABC与△
A′B′C′相似比是
,
△
A′B′C′与△ABC的相似比是 .
2
解:
∵
△
ADE
∽△
ABC,
3.已知△ADE∽△ABC,点A、D、E分别与点
A、B、C对应,且相似比为
,若DE=
4cm,
求BC的长.
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
