4.6 利用相似三角形测高 课件(共23张PPT)
文档属性
| 名称 | 4.6 利用相似三角形测高 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-19 00:00:00 | ||
图片预览








文档简介
(共23张PPT)
北师大版
九年级上
第四章
图形的相似
4.6
利用相似三角形测高
学
习
目
标
1.通过测量旗杆的高度的活动,并复习巩固相似三角形有关知识.(重点)
2.灵活运用三角形相似的知识解决实际问题.(难点)
每个星期一早晨学校都会举行升旗仪式,同学们站在五星红旗下有没有想过我们学校的旗杆有多高呢?怎样利用已学知识测量旗杆的高度?
活动课题:利用相似三角形的有关知识测量旗杆的高度.
活动方式:分组活动、全班交流研讨.
活动工具:小镜子、标杆、皮尺等测量工具.
新课导入
方法1:利用阳光下的影子
方案:如图,选一名同学直立于旗杆影子的顶端处.
知识讲解
(1)能否构建相似的三角形?说明理由.
C
A
E
B
D
方法1:利用阳光下的影子
①同学的身高AB:
②同学的影长BE:
③旗杆的影长DB:
1.6m
0.8m
10m
(2)需要测出哪些长度?
测量工具:皮尺
方法1:利用阳光下的影子
C
A
E
B
D
方法要点:可以把太阳光近似地看成平行光线,计算时用到观测者的身高.
(3)如何求旗杆CD的高?
如果是阴天怎么办呢?
方法1:利用阳光下的影子
C
A
E
B
D
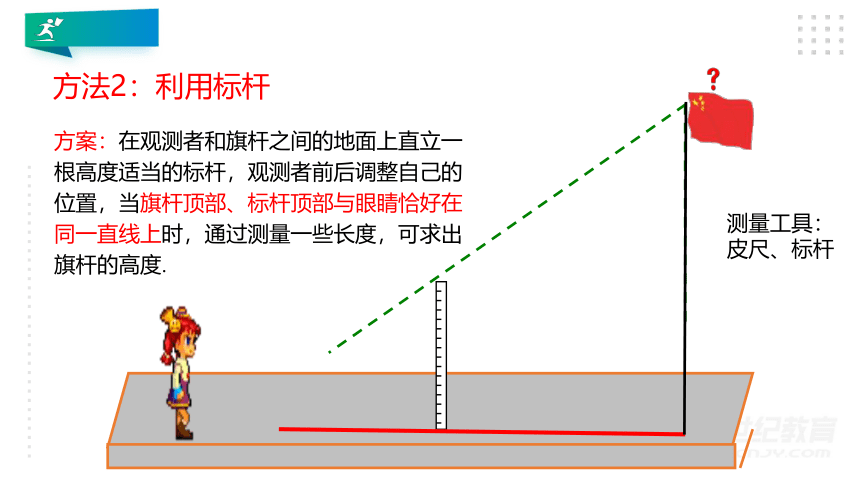
方案:在观测者和旗杆之间的地面上直立一根高度适当的标杆,观测者前后调整自己的位置,当旗杆顶部、标杆顶部与眼睛恰好在同一直线上时,通过测量一些长度,可求出旗杆的高度.
测量工具:
皮尺、标杆
方法2:利用标杆
(1)能否构建相似的三角形呢?说明理由.
N
M
A
C
E
B
F
D
测量工具:皮尺、标杆
方法2:利用标杆
①同学眼睛到地面距离AB:
②标杆的高EF:
③同学到标杆的距离BF:
④同学到旗杆的距离BD:
1.6m
2m
4m
144m
A
N
C
E
M
B
F
D
(2)需要测出哪些长度?
方法2:利用标杆
方法要点:眼睛与标杆的顶端和旗杆的顶端“三点共线”,标杆与地面要垂直,在计算时还要用到观测者的眼睛离地面的高度.
(3)如何求旗杆CD的高?
方法2:利用标杆
A
N
C
E
M
B
F
D
A
C
D
E
B
方案:选一名学生作为观测者,在她与旗杆之间的地面上平放一面镜子,固定镜子的位置,观测者看着镜子来回调整自己的位置,使自己能够通过镜子看到旗杆顶端,测出一些长度就能求出旗杆的高度.
方法3:利用镜子反射
测量工具:
皮尺、镜子
(1)图中的两个三角形是否相似?说明理由.
(2)需要测出哪些长度?
B
D
C
A
E
②同学到镜子中标记的距离BE:
③镜子到旗杆的距离DE:
1.6m
2m
20m
①同学眼睛到地面距离AB:
测量工具:皮尺、镜子
方法3:利用镜子反射
(3)如何求旗杆CD的高?
方法要点:光线的反射角等于入射角.
方法3:利用镜子反射
B
D
C
A
E
1.
上述三种测量方法的基本思路是什么?
(1)测量数据较少,结果较准确;但需要有阳光即影子.
(2)不依靠影子,结果准确;但测量数据较多.
(3)测量数据较少,不依靠影子;但镜子角度有一点误差,结果就会误差很大.
2.
上述几种测量方法各有哪些优缺点?
综合运用三角形相似的判定和性质解决问题,其方法是:
(1)将实际问题转化为相似三角形问题;
(2)想方设法找出一对相似三角形;
(3)根据相似三角形性质,建立比例式,求出相应的量.
1、高4m的旗杆在水平面上的影子长6m,此时测得附近一个建筑物的影子长24m,则该建筑物的高度为
m.
16
随堂训练
2、旗杆的影子长6m,同时测得旗杆顶端到其影子顶端的距离是10m,如果此时附近一纪念塔的影子长30m,那么这座纪念塔的高度为
m.
40
利用相似三角形测高
当被测物体的高度无法直接测量时,我们往往利用相似三角形来测量物体的高度.
利用这三种测量方法,测量的结果允许有误差.
利用阳光下的影子、标杆和镜子反射,测量旗杆的高度.
课堂小结
1.
小明为测量一棵树CD的高度,他在距树24m的点F处直立了一根高为2m的标杆EF,然后小明前后调整自己的位置,当他与树的距离BD为27m时,他的眼睛、标杆的顶端和树顶端在同一直线上,已知小明眼睛到地面的距离AB为1.6m,求树的高度.
A
N
C
E
F
B
D
过点A作AN∥BD交CD于点N,交EF于点M.
∵
∠EMA=∠CNA,∠1=∠1,
∴△AEM∽△ACN,
∴
解:如图,由题意得:AB=1.6m,EF=2m,
BD=27m,FD=24m,
∴
CN=3.6m,CD=3.6+1.6=5.2m
即树高为5.2m.
M
1
当堂检测
解:设树高xm.
∵
∠D=∠B,∠CED=∠AEB,
∴△ABE∽△CDE,
∴
解得
x=12.
答:树高12
m.
3.
如图,在距离树
18m的地面上平放着一面镜子E,人退后到距镜子2.1m的D处,在镜子里恰看见树顶,若人眼距地面1.4m,求树高.
18m
1.4m
2.1m
D
B
C
E
A
https://www.21cnjy.com/help/help_extract.php
北师大版
九年级上
第四章
图形的相似
4.6
利用相似三角形测高
学
习
目
标
1.通过测量旗杆的高度的活动,并复习巩固相似三角形有关知识.(重点)
2.灵活运用三角形相似的知识解决实际问题.(难点)
每个星期一早晨学校都会举行升旗仪式,同学们站在五星红旗下有没有想过我们学校的旗杆有多高呢?怎样利用已学知识测量旗杆的高度?
活动课题:利用相似三角形的有关知识测量旗杆的高度.
活动方式:分组活动、全班交流研讨.
活动工具:小镜子、标杆、皮尺等测量工具.
新课导入
方法1:利用阳光下的影子
方案:如图,选一名同学直立于旗杆影子的顶端处.
知识讲解
(1)能否构建相似的三角形?说明理由.
C
A
E
B
D
方法1:利用阳光下的影子
①同学的身高AB:
②同学的影长BE:
③旗杆的影长DB:
1.6m
0.8m
10m
(2)需要测出哪些长度?
测量工具:皮尺
方法1:利用阳光下的影子
C
A
E
B
D
方法要点:可以把太阳光近似地看成平行光线,计算时用到观测者的身高.
(3)如何求旗杆CD的高?
如果是阴天怎么办呢?
方法1:利用阳光下的影子
C
A
E
B
D
方案:在观测者和旗杆之间的地面上直立一根高度适当的标杆,观测者前后调整自己的位置,当旗杆顶部、标杆顶部与眼睛恰好在同一直线上时,通过测量一些长度,可求出旗杆的高度.
测量工具:
皮尺、标杆
方法2:利用标杆
(1)能否构建相似的三角形呢?说明理由.
N
M
A
C
E
B
F
D
测量工具:皮尺、标杆
方法2:利用标杆
①同学眼睛到地面距离AB:
②标杆的高EF:
③同学到标杆的距离BF:
④同学到旗杆的距离BD:
1.6m
2m
4m
144m
A
N
C
E
M
B
F
D
(2)需要测出哪些长度?
方法2:利用标杆
方法要点:眼睛与标杆的顶端和旗杆的顶端“三点共线”,标杆与地面要垂直,在计算时还要用到观测者的眼睛离地面的高度.
(3)如何求旗杆CD的高?
方法2:利用标杆
A
N
C
E
M
B
F
D
A
C
D
E
B
方案:选一名学生作为观测者,在她与旗杆之间的地面上平放一面镜子,固定镜子的位置,观测者看着镜子来回调整自己的位置,使自己能够通过镜子看到旗杆顶端,测出一些长度就能求出旗杆的高度.
方法3:利用镜子反射
测量工具:
皮尺、镜子
(1)图中的两个三角形是否相似?说明理由.
(2)需要测出哪些长度?
B
D
C
A
E
②同学到镜子中标记的距离BE:
③镜子到旗杆的距离DE:
1.6m
2m
20m
①同学眼睛到地面距离AB:
测量工具:皮尺、镜子
方法3:利用镜子反射
(3)如何求旗杆CD的高?
方法要点:光线的反射角等于入射角.
方法3:利用镜子反射
B
D
C
A
E
1.
上述三种测量方法的基本思路是什么?
(1)测量数据较少,结果较准确;但需要有阳光即影子.
(2)不依靠影子,结果准确;但测量数据较多.
(3)测量数据较少,不依靠影子;但镜子角度有一点误差,结果就会误差很大.
2.
上述几种测量方法各有哪些优缺点?
综合运用三角形相似的判定和性质解决问题,其方法是:
(1)将实际问题转化为相似三角形问题;
(2)想方设法找出一对相似三角形;
(3)根据相似三角形性质,建立比例式,求出相应的量.
1、高4m的旗杆在水平面上的影子长6m,此时测得附近一个建筑物的影子长24m,则该建筑物的高度为
m.
16
随堂训练
2、旗杆的影子长6m,同时测得旗杆顶端到其影子顶端的距离是10m,如果此时附近一纪念塔的影子长30m,那么这座纪念塔的高度为
m.
40
利用相似三角形测高
当被测物体的高度无法直接测量时,我们往往利用相似三角形来测量物体的高度.
利用这三种测量方法,测量的结果允许有误差.
利用阳光下的影子、标杆和镜子反射,测量旗杆的高度.
课堂小结
1.
小明为测量一棵树CD的高度,他在距树24m的点F处直立了一根高为2m的标杆EF,然后小明前后调整自己的位置,当他与树的距离BD为27m时,他的眼睛、标杆的顶端和树顶端在同一直线上,已知小明眼睛到地面的距离AB为1.6m,求树的高度.
A
N
C
E
F
B
D
过点A作AN∥BD交CD于点N,交EF于点M.
∵
∠EMA=∠CNA,∠1=∠1,
∴△AEM∽△ACN,
∴
解:如图,由题意得:AB=1.6m,EF=2m,
BD=27m,FD=24m,
∴
CN=3.6m,CD=3.6+1.6=5.2m
即树高为5.2m.
M
1
当堂检测
解:设树高xm.
∵
∠D=∠B,∠CED=∠AEB,
∴△ABE∽△CDE,
∴
解得
x=12.
答:树高12
m.
3.
如图,在距离树
18m的地面上平放着一面镜子E,人退后到距镜子2.1m的D处,在镜子里恰看见树顶,若人眼距地面1.4m,求树高.
18m
1.4m
2.1m
D
B
C
E
A
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
