【人教版八上高频易错必刷题】11.1 与三角形有关的线段(含解析)
文档属性
| 名称 | 【人教版八上高频易错必刷题】11.1 与三角形有关的线段(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-18 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
11.1
与三角形有关的线段
高频易错必刷题汇编
一、选择题
1.(2021?滨州模拟)三角形按边分类可以用集合来表示,如图所示,图中小椭圆圈里的A表示( )
(?http:?/??/?www.21cnjy.com?)
A.直角三角形
B.锐角三角形
C.钝角三角形
D.等边三角形
2.(2021?长沙模拟)下列长度的三条线段,能组成三角形的是( )
A.4cm,5cm,9cm
B.8cm,8cm,15cm
C.5cm,5cm,10cm
D.6cm,7cm,14cm
3.(2021?柳州模拟)如图,图中直角三角形共有( )
(?http:?/??/?www.21cnjy.com?)
A.1个
B.2个
C.3个
D.4个
4.(2021?成都模拟)已知锐角三角形的边长是2,3,x,那么第三边x的取值范围是( )
A.1<x<
B.
C.
D.
5.(2021?邵阳模拟)如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是( )
A.
(?http:?/??/?www.21cnjy.com?)
B.
(?http:?/??/?www.21cnjy.com?)
C.
(?http:?/??/?www.21cnjy.com?)
D.
(?http:?/??/?www.21cnjy.com?)
6.(2021?无锡模拟)三角形的周长小于13,且各边长为互不相等的整数,则这样的三角形共有( )
A.2个
B.3个
C.4个
D.5个
7.(2021?临沂模拟)如图,工人师傅
(?http:?/??/?www.21cnjy.com?)做了一个长方形窗框ABCD,E、F、G、H分别是四条边上的中点,为了使它稳固,需要在窗框上钉一根木条,这根木条不应钉在( )21教育网
(?http:?/??/?www.21cnjy.com?)
A.A、C两点之间
B.E、G两点之间
C.B、F两点之间
D.G、H两点之间
8.(2021?重庆模拟)如图,CD,CE,CF分别是△ABC的高、角平分线、中线,则下列各式中错误的是( )
(?http:?/??/?www.21cnjy.com?)
A.AB=2BF
B.∠ACE=∠ACB
C.AE=BE
D.CD⊥BE
9.(2021?绍兴模拟)用三角板作△ABC的边BC上的高,下列三角板的摆放位置正确的是( )
A.
(?http:?/??/?www.21cnjy.com?)
B.
(?http:?/??/?www.21cnjy.com?)
C.
(?http:?/??/?www.21cnjy.com?)
D.
(?http:?/??/?www.21cnjy.com?)
10.(2021?贵阳模拟)如图,在△ABC中有四条线段DE,BE,EF,FG,其中有一条线段是△ABC的中线,则该线段是( )www.21-cn-jy.com
(?http:?/??/?www.21cnjy.com?)
A.线段DE
B.线段BE
C.线段EF
D.线段FG
二、填空题
11.(2021?大庆)三个数3,1﹣a,
(?http:?/??/?www.21cnjy.com?)1﹣2a在数轴上从左到右依次排列,且以这三个数为边长能构成三角形,则a的取值范围为
.2·1·c·n·j·y
12.(2021?泰州模拟)若△ABC三条边长为a,b,c,化简:|a+b﹣c|﹣|a﹣c﹣b|=
.
13.(2021?焦作模拟)若有一条公共边的两个三角形称为一对“共边三角形”,则图中以BC为公共边的“共边三角形”有
对.【来源:21·世纪·教育·网】
(?http:?/??/?www.21cnjy.com?)
14.(2021?唐山模拟)如图,AD是△ABC的中线,AE是△ABD的中线,若DE=3cm,则EC=
cm.
(?http:?/??/?www.21cnjy.com?)
15.(2021?厦门模拟)已知:如图所示
(?http:?/??/?www.21cnjy.com?),在△ABC中,点D,E,F分别为BC,AD,CE的中点,且S△ABC=4cm2,则阴影部分的面积为
cm2.21
cnjy
com
(?http:?/??/?www.21cnjy.com?)
16.(2021?成都模拟)原三角形如图所示,如图1,原三角形内部有1个点时,原三角形可被分成3个三角形;
如图2,原三角形内部有2个不同点时,原三角形可被分成5个三角形;
如图3,原三角形内部有3个不同点时,原三角形可被分成7个三角形;
…
以此类推,原三角形内部有n个不同点时,原三角形可被分成
个三角形.
(?http:?/??/?www.21cnjy.com?)
三、解答题
17.(2021?黔东南州
(?http:?/??/?www.21cnjy.com?)模拟)如图,学校有一块三角形空地(即△ABC),现准备将它分成面积相等的两块地,栽种不同的花草,请你把它分出来.(作图题要求:尺规作图,保留作图痕迹,不写作法,不要求证明).
(?http:?/??/?www.21cnjy.com?)
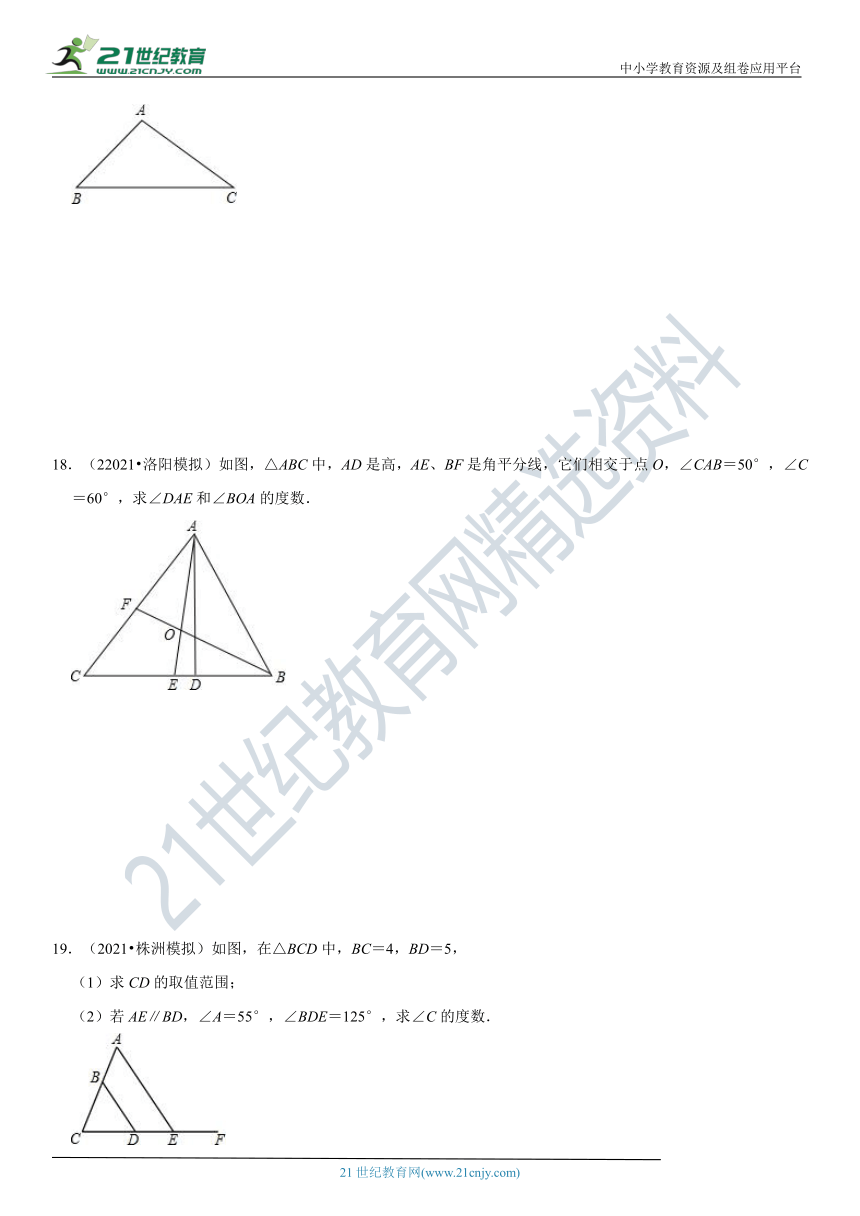
18.(22021?洛阳模拟)如图,△
(?http:?/??/?www.21cnjy.com?)ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠CAB=50°,∠C=60°,求∠DAE和∠BOA的度数.【来源:21cnj
y.co
m】
(?http:?/??/?www.21cnjy.com?)
19.(2021?株洲模拟)如图,在△BCD中,BC=4,BD=5,
(1)求CD的取值范围;
(2)若AE∥BD,∠A=55°,∠BDE=125°,求∠C的度数.
(?http:?/??/?www.21cnjy.com?)
20.(2021?南阳模拟)已知a,b,c是△ABC的三边长,a=4,b=6,设三角形的周长是x.
(1)直接写出c及x的取值范围;
(2)若x是小于18的偶数
①求c的长;
②判断△ABC的形状.
11.1
与三角形有关的线段
高频易错必刷题汇编
一、选择题
1.(2021?滨州模拟)三角形按边分类可以用集合来表示,如图所示,图中小椭圆圈里的A表示( )
(?http:?/??/?www.21cnjy.com?)
A.直角三角形
B.锐角三角形
C.钝角三角形
D.等边三角形
解:三角形根据边分类
(?http:?/??/?www.21cnjy.com?),
∴图中小椭圆圈里的A表示等边三角形.
答案:D.
2.(2021?长沙模拟)下列长度的三条线段,能组成三角形的是( )
A.4cm,5cm,9cm
B.8cm,8cm,15cm
C.5cm,5cm,10cm
D.6cm,7cm,14cm
解:A、∵5+4=9,9=9,
∴该三边不能组成三角形,故此选项错误;
B、8+8=16,16>15,
∴该三边能组成三角形,故此选项正确;
C、5+5=10,10=10,
∴该三边不能组成三角形,故此选项错误;
D、6+7=13,13<14,
∴该三边不能组成三角形,故此选项错误;
答案:B.
3.(2021?柳州模拟)如图,图中直角三角形共有( )
(?http:?/??/?www.21cnjy.com?)
A.1个
B.2个
C.3个
D.4个
解:如图,图中直角三角形有Rt△ABD、Rt△BDC、Rt△ABC,共有3个,
答案:C.
(?http:?/??/?www.21cnjy.com?)
4.(2021?成都模拟)已知锐角三角形的边长是2,3,x,那么第三边x的取值范围是( )
A.1<x<
B.
C.
D.
解:首先要能组成三角形,易得
1<x<5
下面求该三角形为直角三角形的边长情
(?http:?/??/?www.21cnjy.com?)况(此为临界情况),显然长度为2的边对应的角必为锐角(2<3,短边对小角)则只要考虑3或者x为斜边的情况.21cnjy.com
3为斜边时,由勾股定理,22+x2
(?http:?/??/?www.21cnjy.com?)=32,得x=√5
作出图形,固定2边,旋转3边易知当1<x<√5
时,该三角形是以3为最大边的钝角三角形;21·cn·jy·com
x
为斜边时,由勾股定理,22+32=x2,得x=√13,同样作图可得
当√13<x<5时,该三角形是以x为最大边的钝角三角形.【出处:21教育名师】
综上可知,当√5<x<√13
时,原三角形为锐角三角形.
答案:B.
5.(2021?邵阳模拟)如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是( )
A.
(?http:?/??/?www.21cnjy.com?)
B.
(?http:?/??/?www.21cnjy.com?)
C.
(?http:?/??/?www.21cnjy.com?)
D.
(?http:?/??/?www.21cnjy.com?)
解:为△ABC中BC边上的高的是A选项.
答案:A.
6.(2021?无锡模拟)三角形的周长小于13,且各边长为互不相等的整数,则这样的三角形共有( )
A.2个
B.3个
C.4个
D.5个
解:根据三角形的两边之和大于第三边以及三角形的周长小于13,则其中的任何一边不能超过5;
所有的情况有:1、1、1;1、2、2;1、3
(?http:?/??/?www.21cnjy.com?)、3;1、4、4;1、5、5;2、2、2;2、2、3;2、3、3;2、3、4;2、4、4;2、4、5;2、5、5;3、3、3;3、3、4;3、3、5;3、4、4;3、4、5;4、4、4,
再根据两边之差小于第三边,则这样的三角形共有3,4,2;4,5,2;3,4,5三个.
答案:B.
7.(2021?临沂模拟)
(?http:?/??/?www.21cnjy.com?)如图,工人师傅做了一个长方形窗框ABCD,E、F、G、H分别是四条边上的中点,为了使它稳固,需要在窗框上钉一根木条,这根木条不应钉在( )【版权所有:21教育】
(?http:?/??/?www.21cnjy.com?)
A.A、C两点之间
B.E、G两点之间
C.B、F两点之间
D.G、H两点之间
解:工人师傅做了一个长方
(?http:?/??/?www.21cnjy.com?)形窗框ABCD,工人师傅为了使它稳固,需要在窗框上钉一根木条,这根木条不应钉在E、G两点之间(没有构成三角形),这种做法根据的是三角形的稳定性.21教育名师原创作品
答案:B.
8.(2021?重庆模拟)如图,CD,CE,CF分别是△ABC的高、角平分线、中线,则下列各式中错误的是( )
(?http:?/??/?www.21cnjy.com?)
A.AB=2BF
B.∠ACE=∠ACB
C.AE=BE
D.CD⊥BE
解:∵CD,CE,CF分别是△ABC的高、角平分线、中线,
∴CD⊥BE,∠ACE=∠ACB,AB=2BF,无法确定AE=BE.
答案:C.
9.(2021?绍兴模拟)用三角板作△ABC的边BC上的高,下列三角板的摆放位置正确的是( )
A.
(?http:?/??/?www.21cnjy.com?)
B.
(?http:?/??/?www.21cnjy.com?)
C.
(?http:?/??/?www.21cnjy.com?)
D.
(?http:?/??/?www.21cnjy.com?)
解:B,C,D都不是△ABC的边BC上的高,
答案:A.
10.(2021?贵阳模拟)如图,在△ABC中有四条线段DE,BE,EF,FG,其中有一条线段是△ABC的中线,则该线段是( )21世纪教育网版权所有
(?http:?/??/?www.21cnjy.com?)
A.线段DE
B.线段BE
C.线段EF
D.线段FG
解:根据三角形中线的定义知线段BE是△ABC的中线,
答案:B.
二、填空题
11.(2021?大庆)三个数3,1﹣
(?http:?/??/?www.21cnjy.com?)a,1﹣2a在数轴上从左到右依次排列,且以这三个数为边长能构成三角形,则a的取值范围为
﹣3<a<﹣2 .www-2-1-cnjy-com
解:∵3,1﹣a,1﹣2a在数轴上从左到右依次排列,
∴3<1﹣a<1﹣2a,
∴a<﹣2,
∵这三个数为边长能构成三角形,
∴3+(1﹣a)>1﹣2a,
∴a>﹣3,
∴﹣3<a<﹣2,
答案:﹣3<a<﹣2.
12.(2021?泰州模拟)若△ABC三条边长为a,b,c,化简:|a+b﹣c|﹣|a﹣c﹣b|= 2a﹣2c .
解:∵a、b、c为△ABC的三条边长,
∴a+b﹣c>0,a﹣c﹣b<0,
∴原式=a+b﹣c+a﹣c﹣b=2a﹣2c.
答案:2a﹣2c.
13.(2021?焦作模拟)若有一条公共边的两个三角形称为一对“共边三角形”,则图中以BC为公共边的“共边三角形”有 3 对.21·世纪
教育网
(?http:?/??/?www.21cnjy.com?)
解:△BDC与△BEC、△BDC与△BAC、△BEC与△BAC共三对.
答案:3.
14.(2021?唐山模拟)如图,AD是△ABC的中线,AE是△ABD的中线,若DE=3cm,则EC= 9
cm.
(?http:?/??/?www.21cnjy.com?)
解:∵AD是△ABC的中线,AE是△ABD的中线,
∴BD=BC,DE=BE=BD=×BC=BC=3cm,
∴BE=3cm,BC=12cm,
∴EC=BC﹣BE=12﹣3=9cm.
答案:9.
15.(2021?厦门模拟)已知:如图
(?http:?/??/?www.21cnjy.com?)所示,在△ABC中,点D,E,F分别为BC,AD,CE的中点,且S△ABC=4cm2,则阴影部分的面积为 1 cm2.2-1-c-n-j-y
(?http:?/??/?www.21cnjy.com?)
解:∵D为BC中点,根据同底等高的三角形面积相等,
∴S△ABD=S△ACD=S△ABC=×4=2(cm2),
同理S△BDE=S△CDE=S△BCE=×2=1(cm2),
∴S△BCE=2(cm2),
∵F为EC中点,
∴S△BEF=S△BCE=×2=1(cm2).
答案:1.
16.(2021?成都模拟)原三角形如图所示,如图1,原三角形内部有1个点时,原三角形可被分成3个三角形;
如图2,原三角形内部有2个不同点时,原三角形可被分成5个三角形;
如图3,原三角形内部有3个不同点时,原三角形可被分成7个三角形;
…
以此类推,原三角形内部有n个不同点时,原三角形可被分成 2n+1 个三角形.
(?http:?/??/?www.21cnjy.com?)
解:三角形内部每增加一个点,得到三角形的个数正好是比点的个数的2倍还多1个.
答案:2n+1.
三、解答题
17.(2021?黔东南州模拟)如
(?http:?/??/?www.21cnjy.com?)图,学校有一块三角形空地(即△ABC),现准备将它分成面积相等的两块地,栽种不同的花草,请你把它分出来.(作图题要求:尺规作图,保留作图痕迹,不写作法,不要求证明).
(?http:?/??/?www.21cnjy.com?)
解:作图如下:
(?http:?/??/?www.21cnjy.com?).
18.(22021?洛阳模拟)如图,△A
(?http:?/??/?www.21cnjy.com?)BC中,AD是高,AE、BF是角平分线,它们相交于点O,∠CAB=50°,∠C=60°,求∠DAE和∠BOA的度数.21
cnjy
com
(?http:?/??/?www.21cnjy.com?)
解:∵∠CAB=50°,∠C=60°
∴∠ABC=180°﹣50°﹣60°=70°,
又∵AD是高,
∴∠ADC=90°,
∴∠DAC=180°﹣90°﹣∠C=30°,
∵AE、BF是角平分线,
∴∠CBF=∠ABF=35°,∠EAF=25°,
∴∠DAE=∠DAC﹣∠EAF=5°,
∠AFB=∠C+∠CBF=60°+35°=95°,
∴∠BOA=∠EAF+∠AFB=25°+95°=120°,
∴∠DAC=30°,∠BOA=120°.
故∠DAE=5°,∠BOA=120°.
19.(2021?株洲模拟)如图,在△BCD中,BC=4,BD=5,
(1)求CD的取值范围;
(2)若AE∥BD,∠A=55°,∠BDE=125°,求∠C的度数.
(?http:?/??/?www.21cnjy.com?)
解:(1)∵在△BCD中,BC=4,BD=5,
∴1<DC<9;
(2)∵AE∥BD,∠BDE=125°,
∴∠AEC=55°,
又∵∠A=55°,
∴∠C=70°.
20.(2021?南阳模拟)已知a,b,c是△ABC的三边长,a=4,b=6,设三角形的周长是x.
(1)直接写出c及x的取值范围;
(2)若x是小于18的偶数
①求c的长;
②判断△ABC的形状.
解:(1)因为a=4,b=6,
所以2<c<10.
故周长x的范围为12<x<20.
(2)①因为周长为小于18的偶数,
所以x=16或x=14.
当x为16时,c=6;
当x为14时,c=4.
②当c=6时,b=c,△ABC为等腰三角形;
当c=4时,a=c,△ABC为等腰三角形.
综上,△ABC是等腰三角形.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
11.1
与三角形有关的线段
高频易错必刷题汇编
一、选择题
1.(2021?滨州模拟)三角形按边分类可以用集合来表示,如图所示,图中小椭圆圈里的A表示( )
(?http:?/??/?www.21cnjy.com?)
A.直角三角形
B.锐角三角形
C.钝角三角形
D.等边三角形
2.(2021?长沙模拟)下列长度的三条线段,能组成三角形的是( )
A.4cm,5cm,9cm
B.8cm,8cm,15cm
C.5cm,5cm,10cm
D.6cm,7cm,14cm
3.(2021?柳州模拟)如图,图中直角三角形共有( )
(?http:?/??/?www.21cnjy.com?)
A.1个
B.2个
C.3个
D.4个
4.(2021?成都模拟)已知锐角三角形的边长是2,3,x,那么第三边x的取值范围是( )
A.1<x<
B.
C.
D.
5.(2021?邵阳模拟)如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是( )
A.
(?http:?/??/?www.21cnjy.com?)
B.
(?http:?/??/?www.21cnjy.com?)
C.
(?http:?/??/?www.21cnjy.com?)
D.
(?http:?/??/?www.21cnjy.com?)
6.(2021?无锡模拟)三角形的周长小于13,且各边长为互不相等的整数,则这样的三角形共有( )
A.2个
B.3个
C.4个
D.5个
7.(2021?临沂模拟)如图,工人师傅
(?http:?/??/?www.21cnjy.com?)做了一个长方形窗框ABCD,E、F、G、H分别是四条边上的中点,为了使它稳固,需要在窗框上钉一根木条,这根木条不应钉在( )21教育网
(?http:?/??/?www.21cnjy.com?)
A.A、C两点之间
B.E、G两点之间
C.B、F两点之间
D.G、H两点之间
8.(2021?重庆模拟)如图,CD,CE,CF分别是△ABC的高、角平分线、中线,则下列各式中错误的是( )
(?http:?/??/?www.21cnjy.com?)
A.AB=2BF
B.∠ACE=∠ACB
C.AE=BE
D.CD⊥BE
9.(2021?绍兴模拟)用三角板作△ABC的边BC上的高,下列三角板的摆放位置正确的是( )
A.
(?http:?/??/?www.21cnjy.com?)
B.
(?http:?/??/?www.21cnjy.com?)
C.
(?http:?/??/?www.21cnjy.com?)
D.
(?http:?/??/?www.21cnjy.com?)
10.(2021?贵阳模拟)如图,在△ABC中有四条线段DE,BE,EF,FG,其中有一条线段是△ABC的中线,则该线段是( )www.21-cn-jy.com
(?http:?/??/?www.21cnjy.com?)
A.线段DE
B.线段BE
C.线段EF
D.线段FG
二、填空题
11.(2021?大庆)三个数3,1﹣a,
(?http:?/??/?www.21cnjy.com?)1﹣2a在数轴上从左到右依次排列,且以这三个数为边长能构成三角形,则a的取值范围为
.2·1·c·n·j·y
12.(2021?泰州模拟)若△ABC三条边长为a,b,c,化简:|a+b﹣c|﹣|a﹣c﹣b|=
.
13.(2021?焦作模拟)若有一条公共边的两个三角形称为一对“共边三角形”,则图中以BC为公共边的“共边三角形”有
对.【来源:21·世纪·教育·网】
(?http:?/??/?www.21cnjy.com?)
14.(2021?唐山模拟)如图,AD是△ABC的中线,AE是△ABD的中线,若DE=3cm,则EC=
cm.
(?http:?/??/?www.21cnjy.com?)
15.(2021?厦门模拟)已知:如图所示
(?http:?/??/?www.21cnjy.com?),在△ABC中,点D,E,F分别为BC,AD,CE的中点,且S△ABC=4cm2,则阴影部分的面积为
cm2.21
cnjy
com
(?http:?/??/?www.21cnjy.com?)
16.(2021?成都模拟)原三角形如图所示,如图1,原三角形内部有1个点时,原三角形可被分成3个三角形;
如图2,原三角形内部有2个不同点时,原三角形可被分成5个三角形;
如图3,原三角形内部有3个不同点时,原三角形可被分成7个三角形;
…
以此类推,原三角形内部有n个不同点时,原三角形可被分成
个三角形.
(?http:?/??/?www.21cnjy.com?)
三、解答题
17.(2021?黔东南州
(?http:?/??/?www.21cnjy.com?)模拟)如图,学校有一块三角形空地(即△ABC),现准备将它分成面积相等的两块地,栽种不同的花草,请你把它分出来.(作图题要求:尺规作图,保留作图痕迹,不写作法,不要求证明).
(?http:?/??/?www.21cnjy.com?)
18.(22021?洛阳模拟)如图,△
(?http:?/??/?www.21cnjy.com?)ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠CAB=50°,∠C=60°,求∠DAE和∠BOA的度数.【来源:21cnj
y.co
m】
(?http:?/??/?www.21cnjy.com?)
19.(2021?株洲模拟)如图,在△BCD中,BC=4,BD=5,
(1)求CD的取值范围;
(2)若AE∥BD,∠A=55°,∠BDE=125°,求∠C的度数.
(?http:?/??/?www.21cnjy.com?)
20.(2021?南阳模拟)已知a,b,c是△ABC的三边长,a=4,b=6,设三角形的周长是x.
(1)直接写出c及x的取值范围;
(2)若x是小于18的偶数
①求c的长;
②判断△ABC的形状.
11.1
与三角形有关的线段
高频易错必刷题汇编
一、选择题
1.(2021?滨州模拟)三角形按边分类可以用集合来表示,如图所示,图中小椭圆圈里的A表示( )
(?http:?/??/?www.21cnjy.com?)
A.直角三角形
B.锐角三角形
C.钝角三角形
D.等边三角形
解:三角形根据边分类
(?http:?/??/?www.21cnjy.com?),
∴图中小椭圆圈里的A表示等边三角形.
答案:D.
2.(2021?长沙模拟)下列长度的三条线段,能组成三角形的是( )
A.4cm,5cm,9cm
B.8cm,8cm,15cm
C.5cm,5cm,10cm
D.6cm,7cm,14cm
解:A、∵5+4=9,9=9,
∴该三边不能组成三角形,故此选项错误;
B、8+8=16,16>15,
∴该三边能组成三角形,故此选项正确;
C、5+5=10,10=10,
∴该三边不能组成三角形,故此选项错误;
D、6+7=13,13<14,
∴该三边不能组成三角形,故此选项错误;
答案:B.
3.(2021?柳州模拟)如图,图中直角三角形共有( )
(?http:?/??/?www.21cnjy.com?)
A.1个
B.2个
C.3个
D.4个
解:如图,图中直角三角形有Rt△ABD、Rt△BDC、Rt△ABC,共有3个,
答案:C.
(?http:?/??/?www.21cnjy.com?)
4.(2021?成都模拟)已知锐角三角形的边长是2,3,x,那么第三边x的取值范围是( )
A.1<x<
B.
C.
D.
解:首先要能组成三角形,易得
1<x<5
下面求该三角形为直角三角形的边长情
(?http:?/??/?www.21cnjy.com?)况(此为临界情况),显然长度为2的边对应的角必为锐角(2<3,短边对小角)则只要考虑3或者x为斜边的情况.21cnjy.com
3为斜边时,由勾股定理,22+x2
(?http:?/??/?www.21cnjy.com?)=32,得x=√5
作出图形,固定2边,旋转3边易知当1<x<√5
时,该三角形是以3为最大边的钝角三角形;21·cn·jy·com
x
为斜边时,由勾股定理,22+32=x2,得x=√13,同样作图可得
当√13<x<5时,该三角形是以x为最大边的钝角三角形.【出处:21教育名师】
综上可知,当√5<x<√13
时,原三角形为锐角三角形.
答案:B.
5.(2021?邵阳模拟)如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是( )
A.
(?http:?/??/?www.21cnjy.com?)
B.
(?http:?/??/?www.21cnjy.com?)
C.
(?http:?/??/?www.21cnjy.com?)
D.
(?http:?/??/?www.21cnjy.com?)
解:为△ABC中BC边上的高的是A选项.
答案:A.
6.(2021?无锡模拟)三角形的周长小于13,且各边长为互不相等的整数,则这样的三角形共有( )
A.2个
B.3个
C.4个
D.5个
解:根据三角形的两边之和大于第三边以及三角形的周长小于13,则其中的任何一边不能超过5;
所有的情况有:1、1、1;1、2、2;1、3
(?http:?/??/?www.21cnjy.com?)、3;1、4、4;1、5、5;2、2、2;2、2、3;2、3、3;2、3、4;2、4、4;2、4、5;2、5、5;3、3、3;3、3、4;3、3、5;3、4、4;3、4、5;4、4、4,
再根据两边之差小于第三边,则这样的三角形共有3,4,2;4,5,2;3,4,5三个.
答案:B.
7.(2021?临沂模拟)
(?http:?/??/?www.21cnjy.com?)如图,工人师傅做了一个长方形窗框ABCD,E、F、G、H分别是四条边上的中点,为了使它稳固,需要在窗框上钉一根木条,这根木条不应钉在( )【版权所有:21教育】
(?http:?/??/?www.21cnjy.com?)
A.A、C两点之间
B.E、G两点之间
C.B、F两点之间
D.G、H两点之间
解:工人师傅做了一个长方
(?http:?/??/?www.21cnjy.com?)形窗框ABCD,工人师傅为了使它稳固,需要在窗框上钉一根木条,这根木条不应钉在E、G两点之间(没有构成三角形),这种做法根据的是三角形的稳定性.21教育名师原创作品
答案:B.
8.(2021?重庆模拟)如图,CD,CE,CF分别是△ABC的高、角平分线、中线,则下列各式中错误的是( )
(?http:?/??/?www.21cnjy.com?)
A.AB=2BF
B.∠ACE=∠ACB
C.AE=BE
D.CD⊥BE
解:∵CD,CE,CF分别是△ABC的高、角平分线、中线,
∴CD⊥BE,∠ACE=∠ACB,AB=2BF,无法确定AE=BE.
答案:C.
9.(2021?绍兴模拟)用三角板作△ABC的边BC上的高,下列三角板的摆放位置正确的是( )
A.
(?http:?/??/?www.21cnjy.com?)
B.
(?http:?/??/?www.21cnjy.com?)
C.
(?http:?/??/?www.21cnjy.com?)
D.
(?http:?/??/?www.21cnjy.com?)
解:B,C,D都不是△ABC的边BC上的高,
答案:A.
10.(2021?贵阳模拟)如图,在△ABC中有四条线段DE,BE,EF,FG,其中有一条线段是△ABC的中线,则该线段是( )21世纪教育网版权所有
(?http:?/??/?www.21cnjy.com?)
A.线段DE
B.线段BE
C.线段EF
D.线段FG
解:根据三角形中线的定义知线段BE是△ABC的中线,
答案:B.
二、填空题
11.(2021?大庆)三个数3,1﹣
(?http:?/??/?www.21cnjy.com?)a,1﹣2a在数轴上从左到右依次排列,且以这三个数为边长能构成三角形,则a的取值范围为
﹣3<a<﹣2 .www-2-1-cnjy-com
解:∵3,1﹣a,1﹣2a在数轴上从左到右依次排列,
∴3<1﹣a<1﹣2a,
∴a<﹣2,
∵这三个数为边长能构成三角形,
∴3+(1﹣a)>1﹣2a,
∴a>﹣3,
∴﹣3<a<﹣2,
答案:﹣3<a<﹣2.
12.(2021?泰州模拟)若△ABC三条边长为a,b,c,化简:|a+b﹣c|﹣|a﹣c﹣b|= 2a﹣2c .
解:∵a、b、c为△ABC的三条边长,
∴a+b﹣c>0,a﹣c﹣b<0,
∴原式=a+b﹣c+a﹣c﹣b=2a﹣2c.
答案:2a﹣2c.
13.(2021?焦作模拟)若有一条公共边的两个三角形称为一对“共边三角形”,则图中以BC为公共边的“共边三角形”有 3 对.21·世纪
教育网
(?http:?/??/?www.21cnjy.com?)
解:△BDC与△BEC、△BDC与△BAC、△BEC与△BAC共三对.
答案:3.
14.(2021?唐山模拟)如图,AD是△ABC的中线,AE是△ABD的中线,若DE=3cm,则EC= 9
cm.
(?http:?/??/?www.21cnjy.com?)
解:∵AD是△ABC的中线,AE是△ABD的中线,
∴BD=BC,DE=BE=BD=×BC=BC=3cm,
∴BE=3cm,BC=12cm,
∴EC=BC﹣BE=12﹣3=9cm.
答案:9.
15.(2021?厦门模拟)已知:如图
(?http:?/??/?www.21cnjy.com?)所示,在△ABC中,点D,E,F分别为BC,AD,CE的中点,且S△ABC=4cm2,则阴影部分的面积为 1 cm2.2-1-c-n-j-y
(?http:?/??/?www.21cnjy.com?)
解:∵D为BC中点,根据同底等高的三角形面积相等,
∴S△ABD=S△ACD=S△ABC=×4=2(cm2),
同理S△BDE=S△CDE=S△BCE=×2=1(cm2),
∴S△BCE=2(cm2),
∵F为EC中点,
∴S△BEF=S△BCE=×2=1(cm2).
答案:1.
16.(2021?成都模拟)原三角形如图所示,如图1,原三角形内部有1个点时,原三角形可被分成3个三角形;
如图2,原三角形内部有2个不同点时,原三角形可被分成5个三角形;
如图3,原三角形内部有3个不同点时,原三角形可被分成7个三角形;
…
以此类推,原三角形内部有n个不同点时,原三角形可被分成 2n+1 个三角形.
(?http:?/??/?www.21cnjy.com?)
解:三角形内部每增加一个点,得到三角形的个数正好是比点的个数的2倍还多1个.
答案:2n+1.
三、解答题
17.(2021?黔东南州模拟)如
(?http:?/??/?www.21cnjy.com?)图,学校有一块三角形空地(即△ABC),现准备将它分成面积相等的两块地,栽种不同的花草,请你把它分出来.(作图题要求:尺规作图,保留作图痕迹,不写作法,不要求证明).
(?http:?/??/?www.21cnjy.com?)
解:作图如下:
(?http:?/??/?www.21cnjy.com?).
18.(22021?洛阳模拟)如图,△A
(?http:?/??/?www.21cnjy.com?)BC中,AD是高,AE、BF是角平分线,它们相交于点O,∠CAB=50°,∠C=60°,求∠DAE和∠BOA的度数.21
cnjy
com
(?http:?/??/?www.21cnjy.com?)
解:∵∠CAB=50°,∠C=60°
∴∠ABC=180°﹣50°﹣60°=70°,
又∵AD是高,
∴∠ADC=90°,
∴∠DAC=180°﹣90°﹣∠C=30°,
∵AE、BF是角平分线,
∴∠CBF=∠ABF=35°,∠EAF=25°,
∴∠DAE=∠DAC﹣∠EAF=5°,
∠AFB=∠C+∠CBF=60°+35°=95°,
∴∠BOA=∠EAF+∠AFB=25°+95°=120°,
∴∠DAC=30°,∠BOA=120°.
故∠DAE=5°,∠BOA=120°.
19.(2021?株洲模拟)如图,在△BCD中,BC=4,BD=5,
(1)求CD的取值范围;
(2)若AE∥BD,∠A=55°,∠BDE=125°,求∠C的度数.
(?http:?/??/?www.21cnjy.com?)
解:(1)∵在△BCD中,BC=4,BD=5,
∴1<DC<9;
(2)∵AE∥BD,∠BDE=125°,
∴∠AEC=55°,
又∵∠A=55°,
∴∠C=70°.
20.(2021?南阳模拟)已知a,b,c是△ABC的三边长,a=4,b=6,设三角形的周长是x.
(1)直接写出c及x的取值范围;
(2)若x是小于18的偶数
①求c的长;
②判断△ABC的形状.
解:(1)因为a=4,b=6,
所以2<c<10.
故周长x的范围为12<x<20.
(2)①因为周长为小于18的偶数,
所以x=16或x=14.
当x为16时,c=6;
当x为14时,c=4.
②当c=6时,b=c,△ABC为等腰三角形;
当c=4时,a=c,△ABC为等腰三角形.
综上,△ABC是等腰三角形.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
