【人教版八上高频易错必刷题】11.2 与三角形有关的角(含解析)
文档属性
| 名称 | 【人教版八上高频易错必刷题】11.2 与三角形有关的角(含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-18 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
11.2
与三角形有关的角
高频易错必刷题汇编
一、选择题
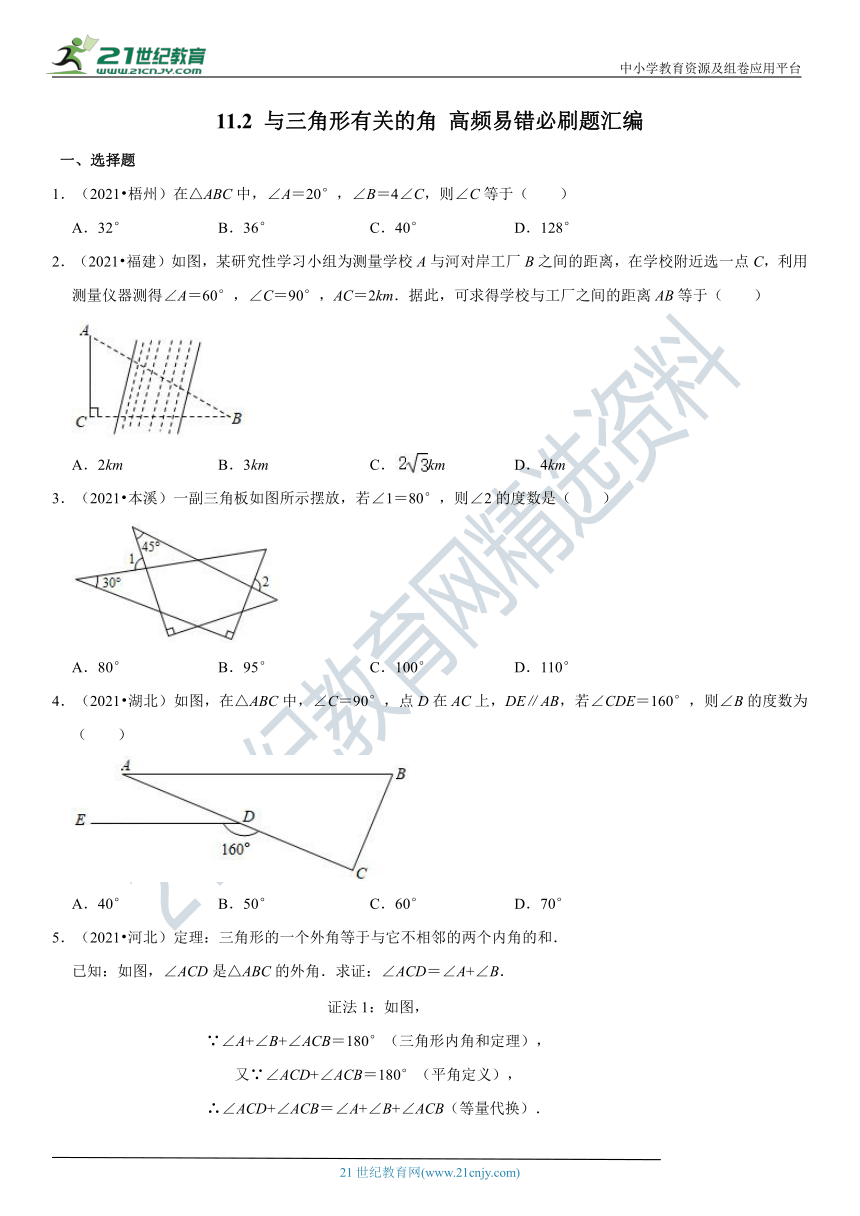
1.(2021?梧州)在△ABC中,∠A=20°,∠B=4∠C,则∠C等于( )
A.32°
B.36°
C.40°
D.128°
2.(2021?福建)如图,
(?http:?/??/?www.21cnjy.com?)某研究性学习小组为测量学校A与河对岸工厂B之间的距离,在学校附近选一点C,利用测量仪器测得∠A=60°,∠C=90°,AC=2km.据此,可求得学校与工厂之间的距离AB等于( )
(?http:?/??/?www.21cnjy.com?)
A.2km
B.3km
C.km
D.4km
3.(2021?本溪)一副三角板如图所示摆放,若∠1=80°,则∠2的度数是( )
(?http:?/??/?www.21cnjy.com?)
A.80°
B.95°
C.100°
D.110°
4.(2021?湖北)如图,在△ABC中,∠C=90°,点D在AC上,DE∥AB,若∠CDE=160°,则∠B的度数为( )21·cn·jy·com
(?http:?/??/?www.21cnjy.com?)
A.40°
B.50°
C.60°
D.70°
5.(2021?河北)定理:三角形的一个外角等于与它不相邻的两个内角的和.
已知:如图,∠ACD是△ABC的外角.求证:∠ACD=∠A+∠B.
证法1:如图,∵∠A+∠B+∠ACB=180°(三角形内角和定理),又∵∠ACD+∠ACB=180°(平角定义),∴∠ACD+∠ACB=∠A+∠B+∠ACB(等量代换).∴∠ACD=∠A+∠B(等式性质).
证法2:如图,∵∠A=76°,∠B=59°,且∠ACD=135°(量角器测量所得)又∵135°=76°+59°(计算所得)∴∠ACD=∠A+∠B(等量代换).
下列说法正确的是( )
(?http:?/??/?www.21cnjy.com?)
A.证法1还需证明其他形状的三角形,该定理的证明才完整
B.证法1用严谨的推理证明了该定理
C.证法2用特殊到一般法证明了该定理
D.证法2只要测量够一百个三角形进行验证,就能证明该定理
6.(2021?宿迁)如图
(?http:?/??/?www.21cnjy.com?),在△ABC中,∠A=70°,∠C=30°,BD平分∠ABC交AC于点D,DE∥AB,交BC于点E,则∠BDE的度数是( )2·1·c·n·j·y
(?http:?/??/?www.21cnjy.com?)
A.30°
B.40°
C.50°
D.60°
7.(2021?陕西)如图,点D、E分别在
(?http:?/??/?www.21cnjy.com?)线段BC、AC上,连接AD、BE.若∠A=35°,∠B=25°,∠C=50°,则∠1的大小为( )21·世纪
教育网
(?http:?/??/?www.21cnjy.com?)
A.60°
B.70°
C.75°
D.85°
8.(2021?乐山)如图,已知直线l1、l2、l3两两相交,且l1⊥l3,若α=50°,则β的度数为( )
(?http:?/??/?www.21cnjy.com?)
A.120°
B.130°
C.140°
D.150°
9.(2020?锦州)如图,在△ABC中,∠A=30°,∠B=50°,CD平分∠ACB,则∠ADC的度数是( )
(?http:?/??/?www.21cnjy.com?)
A.80°
B.90°
C.100°
D.110°
10.(2020?淄博)如图,在四边形ABCD中,CD∥AB,AC⊥BC,若∠B=50°,则∠DCA等于( )
(?http:?/??/?www.21cnjy.com?)
A.30°
B.35°
C.40°
D.45°
二、填空题
11.(2021?常州)如图,在△ABC中,
(?http:?/??/?www.21cnjy.com?)点D、E分别在BC、AC上,∠B=40°,∠C=60°,若DE∥AB,则∠AED=
°.【版权所有:21教育】
(?http:?/??/?www.21cnjy.com?)
12.(2020?泰州)如图,将分别含有30
(?http:?/??/?www.21cnjy.com?)°、45°角的一副三角板重叠,使直角顶点重合,若两直角重叠形成的角为65°,则图中角α的度数为
.21
cnjy
com
(?http:?/??/?www.21cnjy.com?)
13.(2021?绵阳模拟)如图,在△ABC中,BO、CO分别平分∠ABC、∠ACB.若∠BOC=110°,则∠A=
.
(?http:?/??/?www.21cnjy.com?)
14.(2021?枣庄模拟)如图,平面上直线a,b分别经过线段OK两端点(数据如图),则a,b相交所成的锐角是
.
(?http:?/??/?www.21cnjy.com?)
15.(2021?常德模拟)如图,在△ABC中,∠B=40°,三角形的外角∠DAC和∠ACF的平分线交于点E,则∠AEC=
.
(?http:?/??/?www.21cnjy.com?)
16.(2021?河北)如图
(?http:?/??/?www.21cnjy.com?)是可调躺椅示意图(数据如图),AE与BD的交点为C,且∠A,∠B,∠E保持不变.为了舒适,需调整∠D的大小,使∠EFD=110°,则图中∠D应
(填“增加”或“减少”)
度.
(?http:?/??/?www.21cnjy.com?)
三、解答题
17.(2021?淄博模拟)已知:如图,△ABC是任意一个三角形,求证:∠A+∠B+∠C=180°.
(?http:?/??/?www.21cnjy.com?)
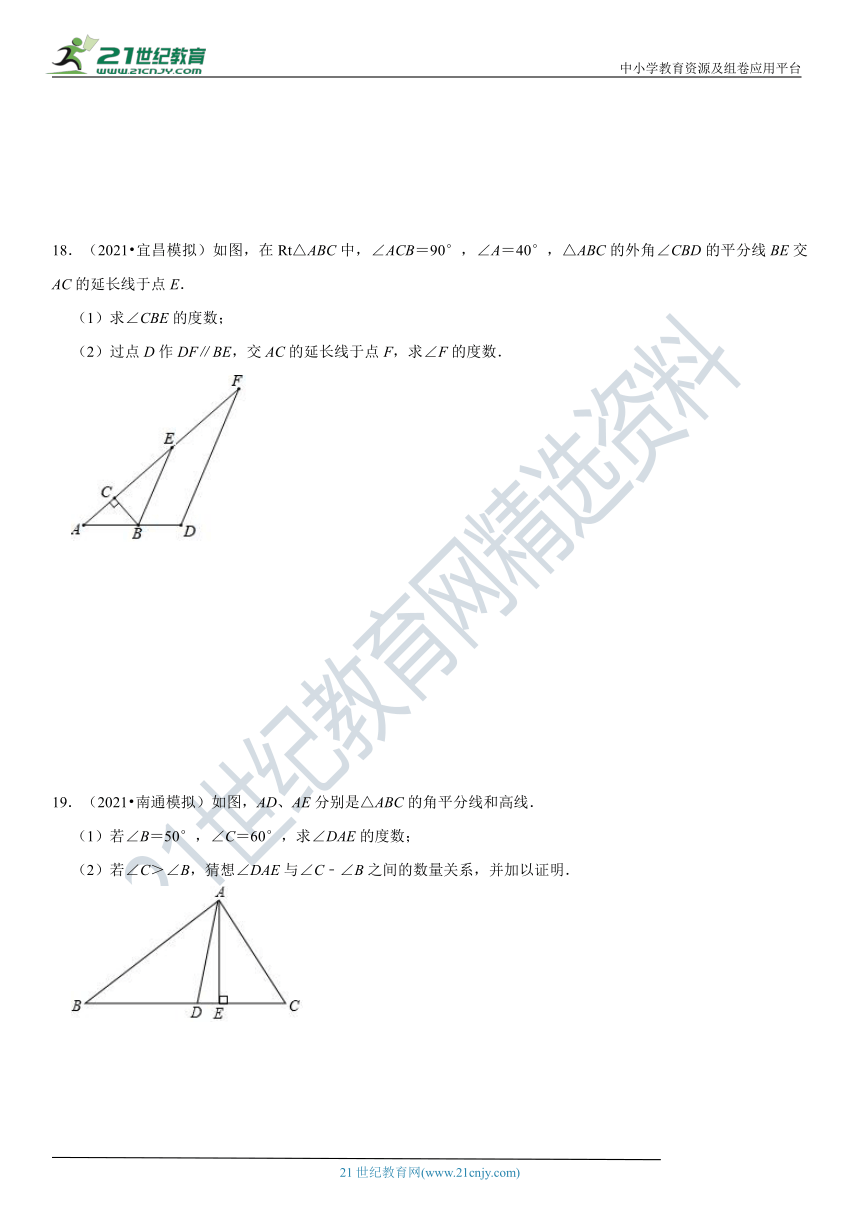
18.(2021?宜昌模拟)如图
(?http:?/??/?www.21cnjy.com?),在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.
(1)求∠CBE的度数;
(2)过点D作DF∥BE,交AC的延长线于点F,求∠F的度数.
(?http:?/??/?www.21cnjy.com?)
19.(2021?南通模拟)如图,AD、AE分别是△ABC的角平分线和高线.
(1)若∠B=50°,∠C=60°,求∠DAE的度数;
(2)若∠C>∠B,猜想∠DAE与∠C﹣∠B之间的数量关系,并加以证明.
(?http:?/??/?www.21cnjy.com?)
20.(2021?青海模拟)认真阅读下面关于三角形内外角平分线所夹角的探究片段,完成所提出的问题.
探究1:如图1,在△ABC中,O是∠ABC与∠ACB的平分线BO和CO的交点,通过分析发现∠BOC=90°+,理由如下:21cnjy.com
∵BO和CO分别是∠ABC和∠ACB的角平分线
∴
∴
又∵∠ABC+∠ACB=180°﹣∠A
∴
∴∠BOC=180°﹣(∠1+∠2)=180°﹣(90°﹣∠A)
=
探究2:如图2中,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?请说明理由.www-2-1-cnjy-com
探究3:如图3中,O是外角∠DBC与外角∠ECB的平分线BO和CO的交点,则∠BOC与∠A有怎样的关系?(只写结论,不需证明)21
cnjy
com
结论:
.
(?http:?/??/?www.21cnjy.com?)
11.2
与三角形有关的角
高频易错必刷题汇编
一、选择题
1.(2021?梧州)在△ABC中,∠A=20°,∠B=4∠C,则∠C等于( )
A.32°
B.36°
C.40°
D.128°
解:∵∠A=20°,∠B=4∠C,
∴在△ABC中,∠A+∠B+∠C=180°,
20°+4∠C+∠C=180°,
5∠C=160°,
∠C=32°.
答案:A.
2.(2021?福建)如图,某研究性学习小
(?http:?/??/?www.21cnjy.com?)组为测量学校A与河对岸工厂B之间的距离,在学校附近选一点C,利用测量仪器测得∠A=60°,∠C=90°,AC=2km.据此,可求得学校与工厂之间的距离AB等于( )
(?http:?/??/?www.21cnjy.com?)
A.2km
B.3km
C.km
D.4km
解:∵∠A=60°,∠C=90°,AC=2km,
∴∠B=30°,
∴AB=2AC=4(km).
答案:D.
3.(2021?本溪)一副三角板如图所示摆放,若∠1=80°,则∠2的度数是( )
(?http:?/??/?www.21cnjy.com?)
A.80°
B.95°
C.100°
D.110°
解:如图,∠5=90°﹣30°=60°,∠3=∠1﹣45°=35°,
∴∠4=∠3=35°,
∴∠2=∠4+∠5=95°,
答案:B.
(?http:?/??/?www.21cnjy.com?)
4.(2021?湖北)如图,在△ABC中,∠C=90°,点D在AC上,DE∥AB,若∠CDE=160°,则∠B的度数为( )
(?http:?/??/?www.21cnjy.com?)
A.40°
B.50°
C.60°
D.70°
解:∵∠CDE=160°,
∴∠ADE=20°,
∵DE∥AB,
∴∠A=∠ADE=20°,
∴∠B=180°﹣∠A﹣∠C=180°﹣20°﹣90°=70°.
答案:D.
5.(2021?河北)定理:三角形的一个外角等于与它不相邻的两个内角的和.
已知:如图,∠ACD是△ABC的外角.求证:∠ACD=∠A+∠B.
证法1:如图,∵∠A+∠B+∠ACB=180°(三角形内角和定理),又∵∠ACD+∠ACB=180°(平角定义),∴∠ACD+∠ACB=∠A+∠B+∠ACB(等量代换).∴∠ACD=∠A+∠B(等式性质).
证法2:如图,∵∠A=76°,∠B=59°,且∠ACD=135°(量角器测量所得)又∵135°=76°+59°(计算所得)∴∠ACD=∠A+∠B(等量代换).
下列说法正确的是( )
(?http:?/??/?www.21cnjy.com?)
A.证法1还需证明其他形状的三角形,该定理的证明才完整
B.证法1用严谨的推理证明了该定理
C.证法2用特殊到一般法证明了该定理
D.证法2只要测量够一百个三角形进行验证,就能证明该定理
解:∵证法1按照定理证明的一般步骤,从已知出发经过严谨的推理论证,得出结论的正确,具有一般性,无需再证明其他形状的三角形,
∴A的说法不正确,不符合题意;
∵证法1按照定理证明的一般步骤,从已知出发经过严谨的推理论证,得出结论的正确,
∴B的说法正确,符合题意;
∵定理的证明必须经过严谨的推理论证,不能用特殊情形来说明,
∴C的说法不正确,不符合题意;
∵定理的证明必须经过严谨的推理论证,与测量次数的多少无关,
∴D的说法不正确,不符合题意;
综上,B的说法正确.
答案:B.
6.(2021?宿迁)如图,在△ABC
(?http:?/??/?www.21cnjy.com?)中,∠A=70°,∠C=30°,BD平分∠ABC交AC于点D,DE∥AB,交BC于点E,则∠BDE的度数是( )21世纪教育网版权所有
(?http:?/??/?www.21cnjy.com?)
A.30°
B.40°
C.50°
D.60°
解:在△ABC中,∠A=70°,∠C=30°,
∴∠ABC=180°﹣∠A﹣∠C=80°,
∵BD平分∠ABC,
∴∠ABD=∠ABC=40°,
∵DE∥AB,
∴∠BDE=∠ABD=40°,
答案:B.
7.(2021?陕西)如图,点D、
(?http:?/??/?www.21cnjy.com?)E分别在线段BC、AC上,连接AD、BE.若∠A=35°,∠B=25°,∠C=50°,则∠1的大小为( )www.21-cn-jy.com
(?http:?/??/?www.21cnjy.com?)
A.60°
B.70°
C.75°
D.85°
解:∵∠1=180﹣(∠B+∠ADB),∠ADB=∠A+∠C,
∴∠1=180°﹣(∠B+∠A+∠C),
∴∠1=180°﹣(25°+35°+50°),
∴∠1=180°﹣110°,
∴∠1=70°,
答案:B.
8.(2021?乐山)如图,已知直线l1、l2、l3两两相交,且l1⊥l3,若α=50°,则β的度数为( )
(?http:?/??/?www.21cnjy.com?)
A.120°
B.130°
C.140°
D.150°
解:如图,根据对顶角相等得:∠1=∠α=50°,
∵l1⊥l3,
∴∠2=90°.
∵∠β是三角形的外角,
∴∠β=∠1+∠2=50°+90°=140°,
答案:C.
(?http:?/??/?www.21cnjy.com?)
9.(2020?锦州)如图,在△ABC中,∠A=30°,∠B=50°,CD平分∠ACB,则∠ADC的度数是( )
(?http:?/??/?www.21cnjy.com?)
A.80°
B.90°
C.100°
D.110°
解:∵∠A=30°,∠B=50°,
∴∠ACB=180°﹣30°﹣50°=100°(三角形内角和定义).
∵CD平分∠ACB,
∴∠BCD=∠ACB=×100°=50°,
∴∠ADC=∠BCD+∠B=50°+50°=100°.
答案:C.
10.(2020?淄博)如图,在四边形ABCD中,CD∥AB,AC⊥BC,若∠B=50°,则∠DCA等于( )
(?http:?/??/?www.21cnjy.com?)
A.30°
B.35°
C.40°
D.45°
解:∵AC⊥BC,
∴∠ACB=90°,
又∵∠B=50°,
∴∠CAB=90°﹣∠B=40°,
∵CD∥AB,
∴∠DCA=∠CAB=40°.
答案:C.
二、填空题
11.(2021?常州)如图,在
(?http:?/??/?www.21cnjy.com?)△ABC中,点D、E分别在BC、AC上,∠B=40°,∠C=60°,若DE∥AB,则∠AED= 100 °.21教育网
(?http:?/??/?www.21cnjy.com?)
解:在△ABC中,∠BAC+∠B+∠C=180°,
∵∠B=40°,∠C=60°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣40°﹣60°=80°,
∵DE∥AB,
∴∠A+∠AED=180°,
∴∠AED=180°﹣80°=100°.
答案:100.
12.(2020?泰州)如图,将分别含
(?http:?/??/?www.21cnjy.com?)有30°、45°角的一副三角板重叠,使直角顶点重合,若两直角重叠形成的角为65°,则图中角α的度数为 140° .2-1-c-n-j-y
(?http:?/??/?www.21cnjy.com?)
解:如图,
(?http:?/??/?www.21cnjy.com?)
∵∠B=30°,∠DCB=65°,
∴∠DFB=∠B+∠DCB=30°+65°=95°,
∴∠α=∠D+∠DFB=45°+95°=140°,
答案:140°.
13.(2021?绵阳模拟)如图,在△ABC中,BO、CO分别平分∠ABC、∠ACB.若∠BOC=110°,则∠A= 40° .
(?http:?/??/?www.21cnjy.com?)
解:∵BO、CO分别平分∠ABC、∠ACB,
∴∠OBC=∠ABC,∠OCB=∠ACB,
而∠BOC+∠OBC+∠OCB=180°,
∴∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣(∠ABC+∠ACB),
∵∠A+∠ABC+∠ACB=180°,
∴∠ABC+∠ACB=180°﹣∠A,
∴∠BOC=180°﹣(180°﹣∠A)=90°+∠A,
而∠BOC=110°,
∴90°+∠A=110°
∴∠A=40°.
故答案为40°.
14.(2021?枣庄模拟)如图,平面上直线a,b分别经过线段OK两端点(数据如图),则a,b相交所成的锐角是 30° .【来源:21cnj
y.co
m】
(?http:?/??/?www.21cnjy.com?)
解:由三角形的外角性质得,a,b相交所成的锐角的度数是100°﹣70°=30°.
答案:30°.
(?http:?/??/?www.21cnjy.com?)
15.(2021?常德模拟)如图,在△ABC中,∠B=40°,三角形的外角∠DAC和∠ACF的平分线交于点E,则∠AEC= 70° .【出处:21教育名师】
(?http:?/??/?www.21cnjy.com?)
解:∵三角形的外角∠DAC和∠ACF的平分线交于点E,
∴∠EAC=∠DAC,∠ECA=∠ACF;
又∵∠B=40°(已知),∠B+∠1+∠2=180°(三角形内角和定理),
∴∠DAC+∠ACF=(∠B+∠2)+(∠B+∠1)=(∠B+∠B+∠1+∠2)=110°(外角定理),
∴∠AEC=180°﹣(∠DAC+∠ACF)=70°.
答案:70°.
(?http:?/??/?www.21cnjy.com?)
16.(2021?河北)如图是可调
(?http:?/??/?www.21cnjy.com?)躺椅示意图(数据如图),AE与BD的交点为C,且∠A,∠B,∠E保持不变.为了舒适,需调整∠D的大小,使∠EFD=110°,则图中∠D应
减少 (填“增加”或“减少”)
10 度.
(?http:?/??/?www.21cnjy.com?)
解:延长EF,交CD于点G,如图:
(?http:?/??/?www.21cnjy.com?)
∵∠ACB=180°﹣50°﹣60°=70°,
∴∠ECD=∠ACB=70°.
∵∠DGF=∠DCE+∠E,
∴∠DGF=70°+30°=100°.
∵∠EFD=110°,∠EFD=∠DGF+∠D,
∴∠D=10°.
而图中∠D=20°,
∴∠D应减少10°.
答案:减少,10.
三、解答题
17.(2021?淄博模拟)已知:如图,△ABC是任意一个三角形,求证:∠A+∠B+∠C=180°.
(?http:?/??/?www.21cnjy.com?)
证明:过点A作EF∥BC,
(?http:?/??/?www.21cnjy.com?)
∵EF∥BC
∴∠1=∠B,∠2=∠C,
∵∠1+∠2+∠BAC=180°,
∴∠BAC+∠B+∠C=180°,
即∠A+∠B+∠C=180°.
18.(2021?宜昌模拟)如图,在
(?http:?/??/?www.21cnjy.com?)Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.21教育名师原创作品
(1)求∠CBE的度数;
(2)过点D作DF∥BE,交AC的延长线于点F,求∠F的度数.
(?http:?/??/?www.21cnjy.com?)
解:(1)∵在Rt△ABC中,∠ACB=90°,∠A=40°,
∴∠ABC=90°﹣∠A=50°,
∴∠CBD=130°.
∵BE是∠CBD的平分线,
∴∠CBE=∠CBD=65°;
(2)∵∠ACB=90°,∠CBE=65°,
∴∠CEB=90°﹣65°=25°.
∵DF∥BE,
∴∠F=∠CEB=25°.
19.(2021?南通模拟)如图,AD、AE分别是△ABC的角平分线和高线.
(1)若∠B=50°,∠C=60°,求∠DAE的度数;
(2)若∠C>∠B,猜想∠DAE与∠C﹣∠B之间的数量关系,并加以证明.
(?http:?/??/?www.21cnjy.com?)
解:(1)在△ABC中,∵∠B=50°,∠C=60°,
∴∠BAC=180°﹣50°﹣60°=70°.
∵AD是∠BAC的角平分线,
∴∠BAD=∠DAC=∠BAC=35°.
又∵AE是BC上的高,
∴∠AEB=90°.
在△BAE中,∠BAE=90°﹣∠B=90°﹣50°=40°,
∴∠DAE=∠BAE﹣∠BAD=40°﹣35°=5°.
(2)∠DAE=(∠C﹣∠B),证明如下:
∵AE是△ABC的高,
∴∠AEC=90°,
∴∠EAC=90°﹣∠C,
∵AD是△ABC的角平分线,
∴∠DAC=∠BAC.
∵∠BAC=180°﹣∠B﹣∠C,
∴∠DAC=(180°﹣∠B﹣∠C),
∴∠DAE=∠DAC﹣∠EAC
=(180°﹣∠B﹣∠C)﹣(90°﹣∠C)
=(∠C﹣∠B).
20.(2021?青海模拟)认真阅读下面关于三角形内外角平分线所夹角的探究片段,完成所提出的问题.
探究1:如图1,在△ABC中,O是∠ABC与∠ACB的平分线BO和CO的交点,通过分析发现∠BOC=90°+,理由如下:【来源:21·世纪·教育·网】
∵BO和CO分别是∠ABC和∠ACB的角平分线
∴
∴
又∵∠ABC+∠ACB=180°﹣∠A
∴
∴∠BOC=180°﹣(∠1+∠2)=180°﹣(90°﹣∠A)
=
探究2:如图2中,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?请说明理由.
探究3:如图3中,O是外角∠DBC与外角∠ECB的平分线BO和CO的交点,则∠BOC与∠A有怎样的关系?(只写结论,不需证明)
结论: ∠BOC=90°﹣∠A .
(?http:?/??/?www.21cnjy.com?)
解:(1)探究2结论:∠BOC=∠A,
理由如下:
∵BO和CO分别是∠ABC和∠ACD的角平分线,
∴∠1=∠ABC,∠2=∠ACD,
又∵∠ACD是△ABC的一外角,
∴∠ACD=∠A+∠ABC,
∴∠2=(∠A+∠ABC)=∠A+∠1,
∵∠2是△BOC的一外角,
∴∠BOC=∠2﹣∠1=∠A+∠1﹣∠1=∠A;
(2)探究3:∠OBC=(∠A+∠ACB),∠OCB=(∠A+∠ABC),
∠BOC=180°﹣∠0BC﹣∠OCB,
=180°﹣(∠A+∠ACB)﹣(∠A+∠ABC),
=180°﹣∠A﹣(∠A+∠ABC+∠ACB),
结论∠BOC=90°﹣∠A.
(?http:?/??/?www.21cnjy.com?)
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
11.2
与三角形有关的角
高频易错必刷题汇编
一、选择题
1.(2021?梧州)在△ABC中,∠A=20°,∠B=4∠C,则∠C等于( )
A.32°
B.36°
C.40°
D.128°
2.(2021?福建)如图,
(?http:?/??/?www.21cnjy.com?)某研究性学习小组为测量学校A与河对岸工厂B之间的距离,在学校附近选一点C,利用测量仪器测得∠A=60°,∠C=90°,AC=2km.据此,可求得学校与工厂之间的距离AB等于( )
(?http:?/??/?www.21cnjy.com?)
A.2km
B.3km
C.km
D.4km
3.(2021?本溪)一副三角板如图所示摆放,若∠1=80°,则∠2的度数是( )
(?http:?/??/?www.21cnjy.com?)
A.80°
B.95°
C.100°
D.110°
4.(2021?湖北)如图,在△ABC中,∠C=90°,点D在AC上,DE∥AB,若∠CDE=160°,则∠B的度数为( )21·cn·jy·com
(?http:?/??/?www.21cnjy.com?)
A.40°
B.50°
C.60°
D.70°
5.(2021?河北)定理:三角形的一个外角等于与它不相邻的两个内角的和.
已知:如图,∠ACD是△ABC的外角.求证:∠ACD=∠A+∠B.
证法1:如图,∵∠A+∠B+∠ACB=180°(三角形内角和定理),又∵∠ACD+∠ACB=180°(平角定义),∴∠ACD+∠ACB=∠A+∠B+∠ACB(等量代换).∴∠ACD=∠A+∠B(等式性质).
证法2:如图,∵∠A=76°,∠B=59°,且∠ACD=135°(量角器测量所得)又∵135°=76°+59°(计算所得)∴∠ACD=∠A+∠B(等量代换).
下列说法正确的是( )
(?http:?/??/?www.21cnjy.com?)
A.证法1还需证明其他形状的三角形,该定理的证明才完整
B.证法1用严谨的推理证明了该定理
C.证法2用特殊到一般法证明了该定理
D.证法2只要测量够一百个三角形进行验证,就能证明该定理
6.(2021?宿迁)如图
(?http:?/??/?www.21cnjy.com?),在△ABC中,∠A=70°,∠C=30°,BD平分∠ABC交AC于点D,DE∥AB,交BC于点E,则∠BDE的度数是( )2·1·c·n·j·y
(?http:?/??/?www.21cnjy.com?)
A.30°
B.40°
C.50°
D.60°
7.(2021?陕西)如图,点D、E分别在
(?http:?/??/?www.21cnjy.com?)线段BC、AC上,连接AD、BE.若∠A=35°,∠B=25°,∠C=50°,则∠1的大小为( )21·世纪
教育网
(?http:?/??/?www.21cnjy.com?)
A.60°
B.70°
C.75°
D.85°
8.(2021?乐山)如图,已知直线l1、l2、l3两两相交,且l1⊥l3,若α=50°,则β的度数为( )
(?http:?/??/?www.21cnjy.com?)
A.120°
B.130°
C.140°
D.150°
9.(2020?锦州)如图,在△ABC中,∠A=30°,∠B=50°,CD平分∠ACB,则∠ADC的度数是( )
(?http:?/??/?www.21cnjy.com?)
A.80°
B.90°
C.100°
D.110°
10.(2020?淄博)如图,在四边形ABCD中,CD∥AB,AC⊥BC,若∠B=50°,则∠DCA等于( )
(?http:?/??/?www.21cnjy.com?)
A.30°
B.35°
C.40°
D.45°
二、填空题
11.(2021?常州)如图,在△ABC中,
(?http:?/??/?www.21cnjy.com?)点D、E分别在BC、AC上,∠B=40°,∠C=60°,若DE∥AB,则∠AED=
°.【版权所有:21教育】
(?http:?/??/?www.21cnjy.com?)
12.(2020?泰州)如图,将分别含有30
(?http:?/??/?www.21cnjy.com?)°、45°角的一副三角板重叠,使直角顶点重合,若两直角重叠形成的角为65°,则图中角α的度数为
.21
cnjy
com
(?http:?/??/?www.21cnjy.com?)
13.(2021?绵阳模拟)如图,在△ABC中,BO、CO分别平分∠ABC、∠ACB.若∠BOC=110°,则∠A=
.
(?http:?/??/?www.21cnjy.com?)
14.(2021?枣庄模拟)如图,平面上直线a,b分别经过线段OK两端点(数据如图),则a,b相交所成的锐角是
.
(?http:?/??/?www.21cnjy.com?)
15.(2021?常德模拟)如图,在△ABC中,∠B=40°,三角形的外角∠DAC和∠ACF的平分线交于点E,则∠AEC=
.
(?http:?/??/?www.21cnjy.com?)
16.(2021?河北)如图
(?http:?/??/?www.21cnjy.com?)是可调躺椅示意图(数据如图),AE与BD的交点为C,且∠A,∠B,∠E保持不变.为了舒适,需调整∠D的大小,使∠EFD=110°,则图中∠D应
(填“增加”或“减少”)
度.
(?http:?/??/?www.21cnjy.com?)
三、解答题
17.(2021?淄博模拟)已知:如图,△ABC是任意一个三角形,求证:∠A+∠B+∠C=180°.
(?http:?/??/?www.21cnjy.com?)
18.(2021?宜昌模拟)如图
(?http:?/??/?www.21cnjy.com?),在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.
(1)求∠CBE的度数;
(2)过点D作DF∥BE,交AC的延长线于点F,求∠F的度数.
(?http:?/??/?www.21cnjy.com?)
19.(2021?南通模拟)如图,AD、AE分别是△ABC的角平分线和高线.
(1)若∠B=50°,∠C=60°,求∠DAE的度数;
(2)若∠C>∠B,猜想∠DAE与∠C﹣∠B之间的数量关系,并加以证明.
(?http:?/??/?www.21cnjy.com?)
20.(2021?青海模拟)认真阅读下面关于三角形内外角平分线所夹角的探究片段,完成所提出的问题.
探究1:如图1,在△ABC中,O是∠ABC与∠ACB的平分线BO和CO的交点,通过分析发现∠BOC=90°+,理由如下:21cnjy.com
∵BO和CO分别是∠ABC和∠ACB的角平分线
∴
∴
又∵∠ABC+∠ACB=180°﹣∠A
∴
∴∠BOC=180°﹣(∠1+∠2)=180°﹣(90°﹣∠A)
=
探究2:如图2中,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?请说明理由.www-2-1-cnjy-com
探究3:如图3中,O是外角∠DBC与外角∠ECB的平分线BO和CO的交点,则∠BOC与∠A有怎样的关系?(只写结论,不需证明)21
cnjy
com
结论:
.
(?http:?/??/?www.21cnjy.com?)
11.2
与三角形有关的角
高频易错必刷题汇编
一、选择题
1.(2021?梧州)在△ABC中,∠A=20°,∠B=4∠C,则∠C等于( )
A.32°
B.36°
C.40°
D.128°
解:∵∠A=20°,∠B=4∠C,
∴在△ABC中,∠A+∠B+∠C=180°,
20°+4∠C+∠C=180°,
5∠C=160°,
∠C=32°.
答案:A.
2.(2021?福建)如图,某研究性学习小
(?http:?/??/?www.21cnjy.com?)组为测量学校A与河对岸工厂B之间的距离,在学校附近选一点C,利用测量仪器测得∠A=60°,∠C=90°,AC=2km.据此,可求得学校与工厂之间的距离AB等于( )
(?http:?/??/?www.21cnjy.com?)
A.2km
B.3km
C.km
D.4km
解:∵∠A=60°,∠C=90°,AC=2km,
∴∠B=30°,
∴AB=2AC=4(km).
答案:D.
3.(2021?本溪)一副三角板如图所示摆放,若∠1=80°,则∠2的度数是( )
(?http:?/??/?www.21cnjy.com?)
A.80°
B.95°
C.100°
D.110°
解:如图,∠5=90°﹣30°=60°,∠3=∠1﹣45°=35°,
∴∠4=∠3=35°,
∴∠2=∠4+∠5=95°,
答案:B.
(?http:?/??/?www.21cnjy.com?)
4.(2021?湖北)如图,在△ABC中,∠C=90°,点D在AC上,DE∥AB,若∠CDE=160°,则∠B的度数为( )
(?http:?/??/?www.21cnjy.com?)
A.40°
B.50°
C.60°
D.70°
解:∵∠CDE=160°,
∴∠ADE=20°,
∵DE∥AB,
∴∠A=∠ADE=20°,
∴∠B=180°﹣∠A﹣∠C=180°﹣20°﹣90°=70°.
答案:D.
5.(2021?河北)定理:三角形的一个外角等于与它不相邻的两个内角的和.
已知:如图,∠ACD是△ABC的外角.求证:∠ACD=∠A+∠B.
证法1:如图,∵∠A+∠B+∠ACB=180°(三角形内角和定理),又∵∠ACD+∠ACB=180°(平角定义),∴∠ACD+∠ACB=∠A+∠B+∠ACB(等量代换).∴∠ACD=∠A+∠B(等式性质).
证法2:如图,∵∠A=76°,∠B=59°,且∠ACD=135°(量角器测量所得)又∵135°=76°+59°(计算所得)∴∠ACD=∠A+∠B(等量代换).
下列说法正确的是( )
(?http:?/??/?www.21cnjy.com?)
A.证法1还需证明其他形状的三角形,该定理的证明才完整
B.证法1用严谨的推理证明了该定理
C.证法2用特殊到一般法证明了该定理
D.证法2只要测量够一百个三角形进行验证,就能证明该定理
解:∵证法1按照定理证明的一般步骤,从已知出发经过严谨的推理论证,得出结论的正确,具有一般性,无需再证明其他形状的三角形,
∴A的说法不正确,不符合题意;
∵证法1按照定理证明的一般步骤,从已知出发经过严谨的推理论证,得出结论的正确,
∴B的说法正确,符合题意;
∵定理的证明必须经过严谨的推理论证,不能用特殊情形来说明,
∴C的说法不正确,不符合题意;
∵定理的证明必须经过严谨的推理论证,与测量次数的多少无关,
∴D的说法不正确,不符合题意;
综上,B的说法正确.
答案:B.
6.(2021?宿迁)如图,在△ABC
(?http:?/??/?www.21cnjy.com?)中,∠A=70°,∠C=30°,BD平分∠ABC交AC于点D,DE∥AB,交BC于点E,则∠BDE的度数是( )21世纪教育网版权所有
(?http:?/??/?www.21cnjy.com?)
A.30°
B.40°
C.50°
D.60°
解:在△ABC中,∠A=70°,∠C=30°,
∴∠ABC=180°﹣∠A﹣∠C=80°,
∵BD平分∠ABC,
∴∠ABD=∠ABC=40°,
∵DE∥AB,
∴∠BDE=∠ABD=40°,
答案:B.
7.(2021?陕西)如图,点D、
(?http:?/??/?www.21cnjy.com?)E分别在线段BC、AC上,连接AD、BE.若∠A=35°,∠B=25°,∠C=50°,则∠1的大小为( )www.21-cn-jy.com
(?http:?/??/?www.21cnjy.com?)
A.60°
B.70°
C.75°
D.85°
解:∵∠1=180﹣(∠B+∠ADB),∠ADB=∠A+∠C,
∴∠1=180°﹣(∠B+∠A+∠C),
∴∠1=180°﹣(25°+35°+50°),
∴∠1=180°﹣110°,
∴∠1=70°,
答案:B.
8.(2021?乐山)如图,已知直线l1、l2、l3两两相交,且l1⊥l3,若α=50°,则β的度数为( )
(?http:?/??/?www.21cnjy.com?)
A.120°
B.130°
C.140°
D.150°
解:如图,根据对顶角相等得:∠1=∠α=50°,
∵l1⊥l3,
∴∠2=90°.
∵∠β是三角形的外角,
∴∠β=∠1+∠2=50°+90°=140°,
答案:C.
(?http:?/??/?www.21cnjy.com?)
9.(2020?锦州)如图,在△ABC中,∠A=30°,∠B=50°,CD平分∠ACB,则∠ADC的度数是( )
(?http:?/??/?www.21cnjy.com?)
A.80°
B.90°
C.100°
D.110°
解:∵∠A=30°,∠B=50°,
∴∠ACB=180°﹣30°﹣50°=100°(三角形内角和定义).
∵CD平分∠ACB,
∴∠BCD=∠ACB=×100°=50°,
∴∠ADC=∠BCD+∠B=50°+50°=100°.
答案:C.
10.(2020?淄博)如图,在四边形ABCD中,CD∥AB,AC⊥BC,若∠B=50°,则∠DCA等于( )
(?http:?/??/?www.21cnjy.com?)
A.30°
B.35°
C.40°
D.45°
解:∵AC⊥BC,
∴∠ACB=90°,
又∵∠B=50°,
∴∠CAB=90°﹣∠B=40°,
∵CD∥AB,
∴∠DCA=∠CAB=40°.
答案:C.
二、填空题
11.(2021?常州)如图,在
(?http:?/??/?www.21cnjy.com?)△ABC中,点D、E分别在BC、AC上,∠B=40°,∠C=60°,若DE∥AB,则∠AED= 100 °.21教育网
(?http:?/??/?www.21cnjy.com?)
解:在△ABC中,∠BAC+∠B+∠C=180°,
∵∠B=40°,∠C=60°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣40°﹣60°=80°,
∵DE∥AB,
∴∠A+∠AED=180°,
∴∠AED=180°﹣80°=100°.
答案:100.
12.(2020?泰州)如图,将分别含
(?http:?/??/?www.21cnjy.com?)有30°、45°角的一副三角板重叠,使直角顶点重合,若两直角重叠形成的角为65°,则图中角α的度数为 140° .2-1-c-n-j-y
(?http:?/??/?www.21cnjy.com?)
解:如图,
(?http:?/??/?www.21cnjy.com?)
∵∠B=30°,∠DCB=65°,
∴∠DFB=∠B+∠DCB=30°+65°=95°,
∴∠α=∠D+∠DFB=45°+95°=140°,
答案:140°.
13.(2021?绵阳模拟)如图,在△ABC中,BO、CO分别平分∠ABC、∠ACB.若∠BOC=110°,则∠A= 40° .
(?http:?/??/?www.21cnjy.com?)
解:∵BO、CO分别平分∠ABC、∠ACB,
∴∠OBC=∠ABC,∠OCB=∠ACB,
而∠BOC+∠OBC+∠OCB=180°,
∴∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣(∠ABC+∠ACB),
∵∠A+∠ABC+∠ACB=180°,
∴∠ABC+∠ACB=180°﹣∠A,
∴∠BOC=180°﹣(180°﹣∠A)=90°+∠A,
而∠BOC=110°,
∴90°+∠A=110°
∴∠A=40°.
故答案为40°.
14.(2021?枣庄模拟)如图,平面上直线a,b分别经过线段OK两端点(数据如图),则a,b相交所成的锐角是 30° .【来源:21cnj
y.co
m】
(?http:?/??/?www.21cnjy.com?)
解:由三角形的外角性质得,a,b相交所成的锐角的度数是100°﹣70°=30°.
答案:30°.
(?http:?/??/?www.21cnjy.com?)
15.(2021?常德模拟)如图,在△ABC中,∠B=40°,三角形的外角∠DAC和∠ACF的平分线交于点E,则∠AEC= 70° .【出处:21教育名师】
(?http:?/??/?www.21cnjy.com?)
解:∵三角形的外角∠DAC和∠ACF的平分线交于点E,
∴∠EAC=∠DAC,∠ECA=∠ACF;
又∵∠B=40°(已知),∠B+∠1+∠2=180°(三角形内角和定理),
∴∠DAC+∠ACF=(∠B+∠2)+(∠B+∠1)=(∠B+∠B+∠1+∠2)=110°(外角定理),
∴∠AEC=180°﹣(∠DAC+∠ACF)=70°.
答案:70°.
(?http:?/??/?www.21cnjy.com?)
16.(2021?河北)如图是可调
(?http:?/??/?www.21cnjy.com?)躺椅示意图(数据如图),AE与BD的交点为C,且∠A,∠B,∠E保持不变.为了舒适,需调整∠D的大小,使∠EFD=110°,则图中∠D应
减少 (填“增加”或“减少”)
10 度.
(?http:?/??/?www.21cnjy.com?)
解:延长EF,交CD于点G,如图:
(?http:?/??/?www.21cnjy.com?)
∵∠ACB=180°﹣50°﹣60°=70°,
∴∠ECD=∠ACB=70°.
∵∠DGF=∠DCE+∠E,
∴∠DGF=70°+30°=100°.
∵∠EFD=110°,∠EFD=∠DGF+∠D,
∴∠D=10°.
而图中∠D=20°,
∴∠D应减少10°.
答案:减少,10.
三、解答题
17.(2021?淄博模拟)已知:如图,△ABC是任意一个三角形,求证:∠A+∠B+∠C=180°.
(?http:?/??/?www.21cnjy.com?)
证明:过点A作EF∥BC,
(?http:?/??/?www.21cnjy.com?)
∵EF∥BC
∴∠1=∠B,∠2=∠C,
∵∠1+∠2+∠BAC=180°,
∴∠BAC+∠B+∠C=180°,
即∠A+∠B+∠C=180°.
18.(2021?宜昌模拟)如图,在
(?http:?/??/?www.21cnjy.com?)Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.21教育名师原创作品
(1)求∠CBE的度数;
(2)过点D作DF∥BE,交AC的延长线于点F,求∠F的度数.
(?http:?/??/?www.21cnjy.com?)
解:(1)∵在Rt△ABC中,∠ACB=90°,∠A=40°,
∴∠ABC=90°﹣∠A=50°,
∴∠CBD=130°.
∵BE是∠CBD的平分线,
∴∠CBE=∠CBD=65°;
(2)∵∠ACB=90°,∠CBE=65°,
∴∠CEB=90°﹣65°=25°.
∵DF∥BE,
∴∠F=∠CEB=25°.
19.(2021?南通模拟)如图,AD、AE分别是△ABC的角平分线和高线.
(1)若∠B=50°,∠C=60°,求∠DAE的度数;
(2)若∠C>∠B,猜想∠DAE与∠C﹣∠B之间的数量关系,并加以证明.
(?http:?/??/?www.21cnjy.com?)
解:(1)在△ABC中,∵∠B=50°,∠C=60°,
∴∠BAC=180°﹣50°﹣60°=70°.
∵AD是∠BAC的角平分线,
∴∠BAD=∠DAC=∠BAC=35°.
又∵AE是BC上的高,
∴∠AEB=90°.
在△BAE中,∠BAE=90°﹣∠B=90°﹣50°=40°,
∴∠DAE=∠BAE﹣∠BAD=40°﹣35°=5°.
(2)∠DAE=(∠C﹣∠B),证明如下:
∵AE是△ABC的高,
∴∠AEC=90°,
∴∠EAC=90°﹣∠C,
∵AD是△ABC的角平分线,
∴∠DAC=∠BAC.
∵∠BAC=180°﹣∠B﹣∠C,
∴∠DAC=(180°﹣∠B﹣∠C),
∴∠DAE=∠DAC﹣∠EAC
=(180°﹣∠B﹣∠C)﹣(90°﹣∠C)
=(∠C﹣∠B).
20.(2021?青海模拟)认真阅读下面关于三角形内外角平分线所夹角的探究片段,完成所提出的问题.
探究1:如图1,在△ABC中,O是∠ABC与∠ACB的平分线BO和CO的交点,通过分析发现∠BOC=90°+,理由如下:【来源:21·世纪·教育·网】
∵BO和CO分别是∠ABC和∠ACB的角平分线
∴
∴
又∵∠ABC+∠ACB=180°﹣∠A
∴
∴∠BOC=180°﹣(∠1+∠2)=180°﹣(90°﹣∠A)
=
探究2:如图2中,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?请说明理由.
探究3:如图3中,O是外角∠DBC与外角∠ECB的平分线BO和CO的交点,则∠BOC与∠A有怎样的关系?(只写结论,不需证明)
结论: ∠BOC=90°﹣∠A .
(?http:?/??/?www.21cnjy.com?)
解:(1)探究2结论:∠BOC=∠A,
理由如下:
∵BO和CO分别是∠ABC和∠ACD的角平分线,
∴∠1=∠ABC,∠2=∠ACD,
又∵∠ACD是△ABC的一外角,
∴∠ACD=∠A+∠ABC,
∴∠2=(∠A+∠ABC)=∠A+∠1,
∵∠2是△BOC的一外角,
∴∠BOC=∠2﹣∠1=∠A+∠1﹣∠1=∠A;
(2)探究3:∠OBC=(∠A+∠ACB),∠OCB=(∠A+∠ABC),
∠BOC=180°﹣∠0BC﹣∠OCB,
=180°﹣(∠A+∠ACB)﹣(∠A+∠ABC),
=180°﹣∠A﹣(∠A+∠ABC+∠ACB),
结论∠BOC=90°﹣∠A.
(?http:?/??/?www.21cnjy.com?)
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
