【人教版八上高频易错必刷题】11.3 多边形及其内角和(含解析)
文档属性
| 名称 | 【人教版八上高频易错必刷题】11.3 多边形及其内角和(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-18 18:22:58 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
11.3
多边形及其内角和
高频易错必刷题汇编
一、选择题
1.(2021?北京)下列多边形中,内角和最大的是( )
A.
B.
C.
D.
2.(2021?眉山)正八边形中,每个内角与每个外角的度数之比为( )
A.1:3
B.1:2
C.2:1
D.3:1
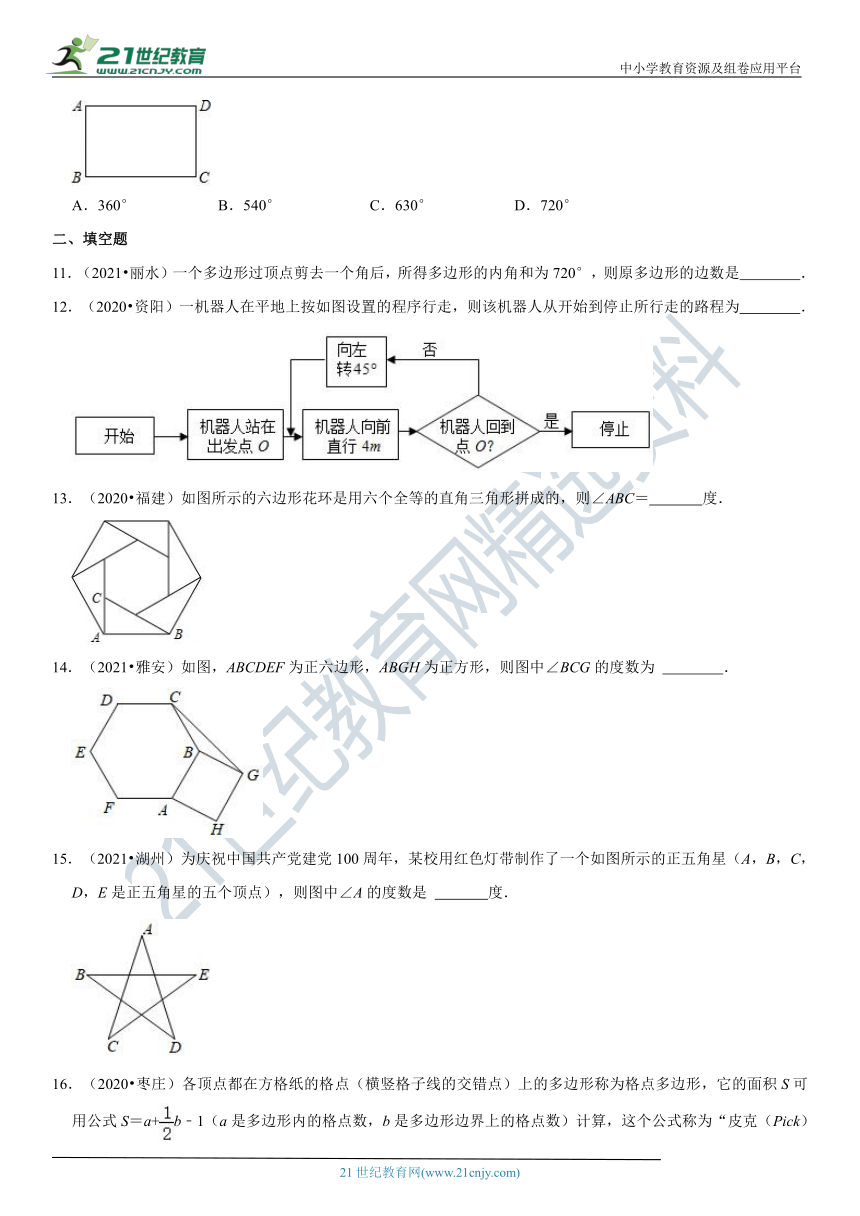
3.(2021?济宁)如图,正五边形ABCDE中,∠CAD的度数为( )
(?http:?/??/?www.21cnjy.com?)
A.72°
B.45°
C.36°
D.35°
4.(2021?福州模拟)如图,∠A+∠B+∠C+∠D+∠E+∠F的值是( )
(?http:?/??/?www.21cnjy.com?)
A.360°
B.480°
C.540°
D.720°
5.(2021?扬州)如图,点A、B、
(?http:?/??/?www.21cnjy.com?)C、D、E在同一平面内,连接AB、BC、CD、DE、EA,若∠BCD=100°,则∠A+∠B+∠D+∠E=( )www-2-1-cnjy-com
(?http:?/??/?www.21cnjy.com?)
A.220°
B.240°
C.260°
D.280°
6.(2021?江西模拟)如图,将正五边形ABCDE绕其顶点A沿逆时针方向旋转,若使点C落在AE边所在的直线上,则旋转的角度可以是( )21世纪教育网版权所有
(?http:?/??/?www.21cnjy.com?)
A.54°
B.72°
C.108°
D.144°
7.(2021?株洲)如图所示,在正六边形ABCDEF内,以AB为边作正五边形ABGHI,则∠FAI=( )
(?http:?/??/?www.21cnjy.com?)
A.10°
B.12°
C.14°
D.15°
8.(2020?广安)如图,在五边形ABCDE中,若去掉一个30°的角后得到一个六边形BCDEMN,则∠1+∠2的度数为( )21
cnjy
com
(?http:?/??/?www.21cnjy.com?)
A.210°
B.110°
C.150°
D.100°
9.(2020?扬州)如图,小明从点A出发沿
(?http:?/??/?www.21cnjy.com?)直线前进10米到达点B,向左转45°后又沿直线前进10米到达点C,再向左转45°后沿直线前进10米到达点D…照这样走下去,小明第一次回到出发点A时所走的路程为( )
(?http:?/??/?www.21cnjy.com?)
A.100米
B.80米
C.60米
D.40米
10.(2021?铜仁模拟)如
(?http:?/??/?www.21cnjy.com?)图为矩形ABCD,一条直线将该矩形分割成两个多边形,若这两个多边形的内角和分别为a和b,则a+b不可能是( )【来源:21cnj
y.co
m】
(?http:?/??/?www.21cnjy.com?)
A.360°
B.540°
C.630°
D.720°
二、填空题
11.(2021?丽水)一个多边形过顶点剪去一个角后,所得多边形的内角和为720°,则原多边形的边数是
.
12.(2020?资阳)一机器人在平地上按如图设置的程序行走,则该机器人从开始到停止所行走的路程为
.
(?http:?/??/?www.21cnjy.com?)
13.(2020?福建)如图所示的六边形花环是用六个全等的直角三角形拼成的,则∠ABC=
度.
(?http:?/??/?www.21cnjy.com?)
14.(2021?雅安)如图,ABCDEF为正六边形,ABGH为正方形,则图中∠BCG的度数为
.
(?http:?/??/?www.21cnjy.com?)
15.(2021?湖州)为庆祝中国
(?http:?/??/?www.21cnjy.com?)共产党建党100周年,某校用红色灯带制作了一个如图所示的正五角星(A,B,C,D,E是正五角星的五个顶点),则图中∠A的度数是
度.21
cnjy
com
(?http:?/??/?www.21cnjy.com?)
16.(2020?枣庄)各顶点都在方格纸的格点(横竖格子线的交错点)上的多边形称为格点多边形,它的面积S可用公式S=a+b﹣1(a是多边形内的格点数,b是多边形边界上的格点数)计算,这个公式称为“皮克(Pick)定理”.如图给出了一个格点五边形,则该五边形的面积S=
.
(?http:?/??/?www.21cnjy.com?)
三、解答题
17.(2021?唐山模拟)在一个多边形中,一个内角相邻的外角与其他各内角的和为600°.
(1)如果这个多边形是五边形,请求出这个外角的度数;
(2)是否存在符合题意的其他多边形?如果存在,请求出边数及这个外角的度数;如果不存在,请说明理由.
18.(2021?衡水模拟)
(?http:?/??/?www.21cnjy.com?)如图,在五边形ABCDE中,∠C=100°,∠D=75°,∠E=135°,AP平分∠EAB,BP平分∠ABC,求∠P的度数.
(?http:?/??/?www.21cnjy.com?)
19.(2021?安徽模拟)如图,一定数量的
(?http:?/??/?www.21cnjy.com?)石子可以摆成如图所示的三角形和四边形,古希腊科学家把数1,3,6,10,15,21,……称为“三角形数“;把1,4,9,16,25,……称为“正方形数“.同样,可以把数1,5,12,22,……,称为“五边形数”,21教育名师原创作品
(?http:?/??/?www.21cnjy.com?)
将三角形、正方形、五边形都整齐的由左到右填在所示表格里:
三角形数
1
3
6
10
15
21
a
…
正方形数
1
4
9
16
25
b
49
…
五边形数
1
5
12
22
c
51
70
…
(1)按照规律,表格中a=
,b=
,c=
;
(2)观察表中规律,第n个“五边形数”是
.
20.(2021?重庆模拟)如图,四边形ABCD中,∠A=∠C=90°,DE平分∠ADC交AB边于点E,BF平分∠ABC交DC边于点F.
求证:DE∥BF.
(?http:?/??/?www.21cnjy.com?)
11.3
多边形及其内角和
高频易错必刷题汇编
一、选择题
1.(2021?北京)下列多边形中,内角和最大的是( )
A.
B.
C.
D.
解:A.三角形的内角和为180°;
B.四边形的内角和为360°;
C.五边形的内角和为:(5﹣2)×180°=540°;
D.六边形的内角和为:(6﹣2)×180°=720°;
答案:D.
2.(2021?眉山)正八边形中,每个内角与每个外角的度数之比为( )
A.1:3
B.1:2
C.2:1
D.3:1
解:这个八边形的内角和为:
(8﹣2)×180°=1080°;
这个八边形的每个内角的度数为:
1080°÷8=135°;
这个八边形的每个外角的度数为:
360°÷8=45°;
∴这个八边形每个内角与每个外角的度数之比为:
135:45=3:1.
答案:D.
3.(2021?济宁)如图,正五边形ABCDE中,∠CAD的度数为( )
(?http:?/??/?www.21cnjy.com?)
A.72°
B.45°
C.36°
D.35°
解:根据正多边形内角和公式可得,
正五边形ABCDE的内角和=180°×(5﹣2)=540°,
则∠BAE=∠B=∠E==108°,
根据正五边形的性质,△ABC≌△AED,
∴∠CAB=∠DAE=(180°﹣108°)=36°,
∴∠CAD=108°﹣36°﹣36°=36°,
答案:C.
4.(2021?福州模拟)如图,∠A+∠B+∠C+∠D+∠E+∠F的值是( )
(?http:?/??/?www.21cnjy.com?)
A.360°
B.480°
C.540°
D.720°
解:如图,AC、DF与BE分别相交于点M、N,
(?http:?/??/?www.21cnjy.com?)
在四边形NMCD中,∠MND+∠CMN+∠C+∠D=360°,
∵∠CMN=∠A+∠E,∠MND=∠B+∠F,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°,
答案:A.
5.(2021?扬州)如图,点A、B、C、
(?http:?/??/?www.21cnjy.com?)D、E在同一平面内,连接AB、BC、CD、DE、EA,若∠BCD=100°,则∠A+∠B+∠D+∠E=( )2·1·c·n·j·y
(?http:?/??/?www.21cnjy.com?)
A.220°
B.240°
C.260°
D.280°
解:连接BD,
(?http:?/??/?www.21cnjy.com?)
∵∠BCD=100°,
∴∠CBD+∠CDB=180°﹣100°=80°,
∴∠A+∠ABC+∠E+∠CDE=360°﹣∠CBD﹣∠CDB=360°﹣80°=280°,
答案:D.
6.(2021?江西模拟)如图,将正五边形ABCDE绕其顶点A沿逆时针方向旋转,若使点C落在AE边所在的直线上,则旋转的角度可以是( )21·世纪
教育网
(?http:?/??/?www.21cnjy.com?)
A.54°
B.72°
C.108°
D.144°
解:连结AC,
(?http:?/??/?www.21cnjy.com?)
∵在正五边形ABCDE中,如右图所示,
∴∠B=∠BAE==108°,
∵BC=BA,
∴∠BCA=∠BAC==36°,
∴∠CAE=∠BAE﹣∠BAC=108°﹣36°=72°,
∴∠CAF=180°﹣∠CAE=180°﹣72°=108°,
∴若点C落在AE边所在的直线上,则旋转的角度可以是108°,
答案:C.
7.(2021?株洲)如图所示,在正六边形ABCDEF内,以AB为边作正五边形ABGHI,则∠FAI=( )
(?http:?/??/?www.21cnjy.com?)
A.10°
B.12°
C.14°
D.15°
解:在正六边形ABCDEF内,正五边形ABGHI中,∠FAB=120°,∠IAB=108°,
∴∠FAI=∠FAB﹣∠IAB=120°﹣108°=12°,
答案:B.
8.(2020?广安)如图,在五边形ABCDE中,若去掉一个30°的角后得到一个六边形BCDEMN,则∠1+∠2的度数为( )2-1-c-n-j-y
(?http:?/??/?www.21cnjy.com?)
A.210°
B.110°
C.150°
D.100°
解:解法一:
∵∠A+∠B+∠C+∠D+∠E=(5﹣2)×180°=540°,∠A=30°,
∴∠B+∠C+∠D+∠E=510°,
∵∠1+∠2+∠B+∠C+∠D+∠E=(6﹣2)×180°=720°,
∴∠1+∠2=720°﹣510°=210°,
解法二:在△ANM中,∠ANM+∠AMN=180°﹣∠A=180°﹣30°=150°,
∴∠1+∠2=360°﹣(∠AMN+∠ANM)=360°﹣150°=210°
答案:A.
9.(2020?扬州)如图,小明从点A出发沿
(?http:?/??/?www.21cnjy.com?)直线前进10米到达点B,向左转45°后又沿直线前进10米到达点C,再向左转45°后沿直线前进10米到达点D…照这样走下去,小明第一次回到出发点A时所走的路程为( )
(?http:?/??/?www.21cnjy.com?)
A.100米
B.80米
C.60米
D.40米
解:∵小明每次都是沿直线前进10米后向左转45度,
∴他走过的图形是正多边形,
∴边数n=360°÷45°=8,
∴他第一次回到出发点A时,一共走了8×10=80(m).
答案:B.
10.(2021?铜仁模拟)如
(?http:?/??/?www.21cnjy.com?)图为矩形ABCD,一条直线将该矩形分割成两个多边形,若这两个多边形的内角和分别为a和b,则a+b不可能是( )21cnjy.com
(?http:?/??/?www.21cnjy.com?)
A.360°
B.540°
C.630°
D.720°
解:一条直线将该矩形ABCD分割成两个多边形,每一个多边形的内角和都是180°的倍数,都能被180整除,分析四个答案,【版权所有:21教育】
只有630不能被180整除,所以a+b不可能是630°.
答案:C.
二、填空题
11.(2021?丽水)一个多边形过顶点剪去一个角后,所得多边形的内角和为720°,则原多边形的边数是 6或7 .
解:设内角和为720°的多边形的边数是n,则(n﹣2)?180=720,
解得:n=6.
∵多边形过顶点截去一个角后边数不变或减少1,
∴原多边形的边数为6或7,
答案:6或7.
12.(2020?资阳)一机器人在平地上按如图设置的程序行走,则该机器人从开始到停止所行走的路程为 32m .
(?http:?/??/?www.21cnjy.com?)
解:该机器人所经过的路径是一个正多边形,
360°÷45°=8,
则所走的路程是:4×8=32(m).
答案:32m.
13.(2020?福建)如图所示的六边形花环是用六个全等的直角三角形拼成的,则∠ABC= 30 度.
(?http:?/??/?www.21cnjy.com?)
解:正六边形的每个内角的度数为:=120°,
所以∠ABC=120°﹣90°=30°,
答案:30.
14.(2021?雅安)如图,ABCDEF为正六边形,ABGH为正方形,则图中∠BCG的度数为
15° .
(?http:?/??/?www.21cnjy.com?)
解:∵ABCDEF为正六边形,ABGH为正方形,
∴AB=BC=BG,
∴∠BCG=∠BGC,
∵正六边形ABCDEF的每一个内角是4×180°÷6=120°,
正方形ABGH的每个内角是90°,
∴∠CBG=360°﹣120°﹣90°=150°,
∴∠BCG+∠BGC=180°﹣150°=30°,
∴∠BCG=15°.
答案:15°.
15.(2021?湖州)为庆祝中国共产党建党
(?http:?/??/?www.21cnjy.com?)100周年,某校用红色灯带制作了一个如图所示的正五角星(A,B,C,D,E是正五角星的五个顶点),则图中∠A的度数是
36 度.【来源:21·世纪·教育·网】
(?http:?/??/?www.21cnjy.com?)
解:如图,
(?http:?/??/?www.21cnjy.com?)
∵正五角星中,五边形FGHMN是正五边形,
∴∠GFN=∠FNM==108°,
∴∠AFN=∠ANF=180°﹣∠GFN=180°﹣108°=72°,
∴∠A=180°﹣∠AFN﹣∠ANF=180°﹣72°﹣72°=36°.
答案:36.
16.(2020?枣庄)各顶点都在方格纸的格点(横竖格子线的交错点)上的多边形称为格点多边形,它的面积S可用公式S=a+b﹣1(a是多边形内的格点数,b是多边形边界上的格点数)计算,这个公式称为“皮克(Pick)定理”.如图给出了一个格点五边形,则该五边形的面积S= 6 .21·cn·jy·com
(?http:?/??/?www.21cnjy.com?)
解:a表示多边形内部的格点数,b表示多边形边界上的格点数,S表示多边形的面积,
通过图象可知a=4,b=6,
∴该五边形的面积S=4+×6﹣1=6,
答案:6.
三、解答题
17.(2021?唐山模拟)在一个多边形中,一个内角相邻的外角与其他各内角的和为600°.
(1)如果这个多边形是五边形,请求出这个外角的度数;
(2)是否存在符合题意的其他多边形?如果存在,请求出边数及这个外角的度数;如果不存在,请说明理由.
解:
(1)设这个外角的度数是x°,则
(5﹣2)×180﹣(180﹣x)+x=600,
解得x=120.
故这个外角的度数是120°.
(2)存在.
设边数为n,这个外角的度数是x°,则
(n﹣2)×180﹣(180﹣x)+x=600,
整理得x=570﹣90n,
∵0<x<180,
即0<570﹣90n<180,并且n为正整数,
∴n=5或n=6.
故这个多边形的边数是6,这个外角的度数为30°.
18.(2021?衡水模拟
(?http:?/??/?www.21cnjy.com?))如图,在五边形ABCDE中,∠C=100°,∠D=75°,∠E=135°,AP平分∠EAB,BP平分∠ABC,求∠P的度数.【出处:21教育名师】
(?http:?/??/?www.21cnjy.com?)
解:∵∠EAB+∠ABC+∠C+∠D+∠E=540°,∠C=100°,∠D=75°,∠E=135°
∴∠EAB+∠ABC=540°﹣∠C﹣∠D﹣∠E=230°,
∵AP平分∠EAB
∴,
同理可得,,
∵∠P+∠PAB+∠PBA=180°,
∴∠P=180°﹣∠PAB﹣∠PBA====65°.
19.(2021?安徽模拟
(?http:?/??/?www.21cnjy.com?))如图,一定数量的石子可以摆成如图所示的三角形和四边形,古希腊科学家把数1,3,6,10,15,21,……称为“三角形数“;把1,4,9,16,25,……称为“正方形数“.同样,可以把数1,5,12,22,……,称为“五边形数”,www.21-cn-jy.com
(?http:?/??/?www.21cnjy.com?)
将三角形、正方形、五边形都整齐的由左到右填在所示表格里:
三角形数
1
3
6
10
15
21
a
…
正方形数
1
4
9
16
25
b
49
…
五边形数
1
5
12
22
c
51
70
…
(1)按照规律,表格中a= 28 ,b= 36 ,c= 35 ;
(2)观察表中规律,第n个“五边形数”是 .
解:(1)∵前6个“三角形数”分别是:
1=、3=、6=、10=、15=、21=,
∴第n个“三角形数”是,
∴a==28.
∵前5个“正方形数”分别是:
1=12,4=22,9=32,16=42,25=52,
∴第n个“正方形数”是n2,
∴b=62=36.
∵前4个“五边形数”分别是:
1=,5=,12=,22=,
∴c==35.
(2)根据(1)中的规律得出:第n个“五边形数”是;
答案:.
20.(2021?重庆模拟)如图,四边形ABCD中,∠A=∠C=90°,DE平分∠ADC交AB边于点E,BF平分∠ABC交DC边于点F.21教育网
求证:DE∥BF.
(?http:?/??/?www.21cnjy.com?)
证明:∵四边形ABCD中,∠A=∠C=90°,
∴∠ADC+∠ABC=180°,
∵DE平分∠ADC交AB边于点E,BF平分∠ABC交DC边于点F,
∴∠ADE=∠EDC,∠ABF=∠CBF,
∴∠ADE+∠FBC=90°,
∵∠AED+∠ADE=90°,∠ADE=∠EDC,
∴∠AED=∠ABF,
∴DE∥BF.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
11.3
多边形及其内角和
高频易错必刷题汇编
一、选择题
1.(2021?北京)下列多边形中,内角和最大的是( )
A.
B.
C.
D.
2.(2021?眉山)正八边形中,每个内角与每个外角的度数之比为( )
A.1:3
B.1:2
C.2:1
D.3:1
3.(2021?济宁)如图,正五边形ABCDE中,∠CAD的度数为( )
(?http:?/??/?www.21cnjy.com?)
A.72°
B.45°
C.36°
D.35°
4.(2021?福州模拟)如图,∠A+∠B+∠C+∠D+∠E+∠F的值是( )
(?http:?/??/?www.21cnjy.com?)
A.360°
B.480°
C.540°
D.720°
5.(2021?扬州)如图,点A、B、
(?http:?/??/?www.21cnjy.com?)C、D、E在同一平面内,连接AB、BC、CD、DE、EA,若∠BCD=100°,则∠A+∠B+∠D+∠E=( )www-2-1-cnjy-com
(?http:?/??/?www.21cnjy.com?)
A.220°
B.240°
C.260°
D.280°
6.(2021?江西模拟)如图,将正五边形ABCDE绕其顶点A沿逆时针方向旋转,若使点C落在AE边所在的直线上,则旋转的角度可以是( )21世纪教育网版权所有
(?http:?/??/?www.21cnjy.com?)
A.54°
B.72°
C.108°
D.144°
7.(2021?株洲)如图所示,在正六边形ABCDEF内,以AB为边作正五边形ABGHI,则∠FAI=( )
(?http:?/??/?www.21cnjy.com?)
A.10°
B.12°
C.14°
D.15°
8.(2020?广安)如图,在五边形ABCDE中,若去掉一个30°的角后得到一个六边形BCDEMN,则∠1+∠2的度数为( )21
cnjy
com
(?http:?/??/?www.21cnjy.com?)
A.210°
B.110°
C.150°
D.100°
9.(2020?扬州)如图,小明从点A出发沿
(?http:?/??/?www.21cnjy.com?)直线前进10米到达点B,向左转45°后又沿直线前进10米到达点C,再向左转45°后沿直线前进10米到达点D…照这样走下去,小明第一次回到出发点A时所走的路程为( )
(?http:?/??/?www.21cnjy.com?)
A.100米
B.80米
C.60米
D.40米
10.(2021?铜仁模拟)如
(?http:?/??/?www.21cnjy.com?)图为矩形ABCD,一条直线将该矩形分割成两个多边形,若这两个多边形的内角和分别为a和b,则a+b不可能是( )【来源:21cnj
y.co
m】
(?http:?/??/?www.21cnjy.com?)
A.360°
B.540°
C.630°
D.720°
二、填空题
11.(2021?丽水)一个多边形过顶点剪去一个角后,所得多边形的内角和为720°,则原多边形的边数是
.
12.(2020?资阳)一机器人在平地上按如图设置的程序行走,则该机器人从开始到停止所行走的路程为
.
(?http:?/??/?www.21cnjy.com?)
13.(2020?福建)如图所示的六边形花环是用六个全等的直角三角形拼成的,则∠ABC=
度.
(?http:?/??/?www.21cnjy.com?)
14.(2021?雅安)如图,ABCDEF为正六边形,ABGH为正方形,则图中∠BCG的度数为
.
(?http:?/??/?www.21cnjy.com?)
15.(2021?湖州)为庆祝中国
(?http:?/??/?www.21cnjy.com?)共产党建党100周年,某校用红色灯带制作了一个如图所示的正五角星(A,B,C,D,E是正五角星的五个顶点),则图中∠A的度数是
度.21
cnjy
com
(?http:?/??/?www.21cnjy.com?)
16.(2020?枣庄)各顶点都在方格纸的格点(横竖格子线的交错点)上的多边形称为格点多边形,它的面积S可用公式S=a+b﹣1(a是多边形内的格点数,b是多边形边界上的格点数)计算,这个公式称为“皮克(Pick)定理”.如图给出了一个格点五边形,则该五边形的面积S=
.
(?http:?/??/?www.21cnjy.com?)
三、解答题
17.(2021?唐山模拟)在一个多边形中,一个内角相邻的外角与其他各内角的和为600°.
(1)如果这个多边形是五边形,请求出这个外角的度数;
(2)是否存在符合题意的其他多边形?如果存在,请求出边数及这个外角的度数;如果不存在,请说明理由.
18.(2021?衡水模拟)
(?http:?/??/?www.21cnjy.com?)如图,在五边形ABCDE中,∠C=100°,∠D=75°,∠E=135°,AP平分∠EAB,BP平分∠ABC,求∠P的度数.
(?http:?/??/?www.21cnjy.com?)
19.(2021?安徽模拟)如图,一定数量的
(?http:?/??/?www.21cnjy.com?)石子可以摆成如图所示的三角形和四边形,古希腊科学家把数1,3,6,10,15,21,……称为“三角形数“;把1,4,9,16,25,……称为“正方形数“.同样,可以把数1,5,12,22,……,称为“五边形数”,21教育名师原创作品
(?http:?/??/?www.21cnjy.com?)
将三角形、正方形、五边形都整齐的由左到右填在所示表格里:
三角形数
1
3
6
10
15
21
a
…
正方形数
1
4
9
16
25
b
49
…
五边形数
1
5
12
22
c
51
70
…
(1)按照规律,表格中a=
,b=
,c=
;
(2)观察表中规律,第n个“五边形数”是
.
20.(2021?重庆模拟)如图,四边形ABCD中,∠A=∠C=90°,DE平分∠ADC交AB边于点E,BF平分∠ABC交DC边于点F.
求证:DE∥BF.
(?http:?/??/?www.21cnjy.com?)
11.3
多边形及其内角和
高频易错必刷题汇编
一、选择题
1.(2021?北京)下列多边形中,内角和最大的是( )
A.
B.
C.
D.
解:A.三角形的内角和为180°;
B.四边形的内角和为360°;
C.五边形的内角和为:(5﹣2)×180°=540°;
D.六边形的内角和为:(6﹣2)×180°=720°;
答案:D.
2.(2021?眉山)正八边形中,每个内角与每个外角的度数之比为( )
A.1:3
B.1:2
C.2:1
D.3:1
解:这个八边形的内角和为:
(8﹣2)×180°=1080°;
这个八边形的每个内角的度数为:
1080°÷8=135°;
这个八边形的每个外角的度数为:
360°÷8=45°;
∴这个八边形每个内角与每个外角的度数之比为:
135:45=3:1.
答案:D.
3.(2021?济宁)如图,正五边形ABCDE中,∠CAD的度数为( )
(?http:?/??/?www.21cnjy.com?)
A.72°
B.45°
C.36°
D.35°
解:根据正多边形内角和公式可得,
正五边形ABCDE的内角和=180°×(5﹣2)=540°,
则∠BAE=∠B=∠E==108°,
根据正五边形的性质,△ABC≌△AED,
∴∠CAB=∠DAE=(180°﹣108°)=36°,
∴∠CAD=108°﹣36°﹣36°=36°,
答案:C.
4.(2021?福州模拟)如图,∠A+∠B+∠C+∠D+∠E+∠F的值是( )
(?http:?/??/?www.21cnjy.com?)
A.360°
B.480°
C.540°
D.720°
解:如图,AC、DF与BE分别相交于点M、N,
(?http:?/??/?www.21cnjy.com?)
在四边形NMCD中,∠MND+∠CMN+∠C+∠D=360°,
∵∠CMN=∠A+∠E,∠MND=∠B+∠F,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°,
答案:A.
5.(2021?扬州)如图,点A、B、C、
(?http:?/??/?www.21cnjy.com?)D、E在同一平面内,连接AB、BC、CD、DE、EA,若∠BCD=100°,则∠A+∠B+∠D+∠E=( )2·1·c·n·j·y
(?http:?/??/?www.21cnjy.com?)
A.220°
B.240°
C.260°
D.280°
解:连接BD,
(?http:?/??/?www.21cnjy.com?)
∵∠BCD=100°,
∴∠CBD+∠CDB=180°﹣100°=80°,
∴∠A+∠ABC+∠E+∠CDE=360°﹣∠CBD﹣∠CDB=360°﹣80°=280°,
答案:D.
6.(2021?江西模拟)如图,将正五边形ABCDE绕其顶点A沿逆时针方向旋转,若使点C落在AE边所在的直线上,则旋转的角度可以是( )21·世纪
教育网
(?http:?/??/?www.21cnjy.com?)
A.54°
B.72°
C.108°
D.144°
解:连结AC,
(?http:?/??/?www.21cnjy.com?)
∵在正五边形ABCDE中,如右图所示,
∴∠B=∠BAE==108°,
∵BC=BA,
∴∠BCA=∠BAC==36°,
∴∠CAE=∠BAE﹣∠BAC=108°﹣36°=72°,
∴∠CAF=180°﹣∠CAE=180°﹣72°=108°,
∴若点C落在AE边所在的直线上,则旋转的角度可以是108°,
答案:C.
7.(2021?株洲)如图所示,在正六边形ABCDEF内,以AB为边作正五边形ABGHI,则∠FAI=( )
(?http:?/??/?www.21cnjy.com?)
A.10°
B.12°
C.14°
D.15°
解:在正六边形ABCDEF内,正五边形ABGHI中,∠FAB=120°,∠IAB=108°,
∴∠FAI=∠FAB﹣∠IAB=120°﹣108°=12°,
答案:B.
8.(2020?广安)如图,在五边形ABCDE中,若去掉一个30°的角后得到一个六边形BCDEMN,则∠1+∠2的度数为( )2-1-c-n-j-y
(?http:?/??/?www.21cnjy.com?)
A.210°
B.110°
C.150°
D.100°
解:解法一:
∵∠A+∠B+∠C+∠D+∠E=(5﹣2)×180°=540°,∠A=30°,
∴∠B+∠C+∠D+∠E=510°,
∵∠1+∠2+∠B+∠C+∠D+∠E=(6﹣2)×180°=720°,
∴∠1+∠2=720°﹣510°=210°,
解法二:在△ANM中,∠ANM+∠AMN=180°﹣∠A=180°﹣30°=150°,
∴∠1+∠2=360°﹣(∠AMN+∠ANM)=360°﹣150°=210°
答案:A.
9.(2020?扬州)如图,小明从点A出发沿
(?http:?/??/?www.21cnjy.com?)直线前进10米到达点B,向左转45°后又沿直线前进10米到达点C,再向左转45°后沿直线前进10米到达点D…照这样走下去,小明第一次回到出发点A时所走的路程为( )
(?http:?/??/?www.21cnjy.com?)
A.100米
B.80米
C.60米
D.40米
解:∵小明每次都是沿直线前进10米后向左转45度,
∴他走过的图形是正多边形,
∴边数n=360°÷45°=8,
∴他第一次回到出发点A时,一共走了8×10=80(m).
答案:B.
10.(2021?铜仁模拟)如
(?http:?/??/?www.21cnjy.com?)图为矩形ABCD,一条直线将该矩形分割成两个多边形,若这两个多边形的内角和分别为a和b,则a+b不可能是( )21cnjy.com
(?http:?/??/?www.21cnjy.com?)
A.360°
B.540°
C.630°
D.720°
解:一条直线将该矩形ABCD分割成两个多边形,每一个多边形的内角和都是180°的倍数,都能被180整除,分析四个答案,【版权所有:21教育】
只有630不能被180整除,所以a+b不可能是630°.
答案:C.
二、填空题
11.(2021?丽水)一个多边形过顶点剪去一个角后,所得多边形的内角和为720°,则原多边形的边数是 6或7 .
解:设内角和为720°的多边形的边数是n,则(n﹣2)?180=720,
解得:n=6.
∵多边形过顶点截去一个角后边数不变或减少1,
∴原多边形的边数为6或7,
答案:6或7.
12.(2020?资阳)一机器人在平地上按如图设置的程序行走,则该机器人从开始到停止所行走的路程为 32m .
(?http:?/??/?www.21cnjy.com?)
解:该机器人所经过的路径是一个正多边形,
360°÷45°=8,
则所走的路程是:4×8=32(m).
答案:32m.
13.(2020?福建)如图所示的六边形花环是用六个全等的直角三角形拼成的,则∠ABC= 30 度.
(?http:?/??/?www.21cnjy.com?)
解:正六边形的每个内角的度数为:=120°,
所以∠ABC=120°﹣90°=30°,
答案:30.
14.(2021?雅安)如图,ABCDEF为正六边形,ABGH为正方形,则图中∠BCG的度数为
15° .
(?http:?/??/?www.21cnjy.com?)
解:∵ABCDEF为正六边形,ABGH为正方形,
∴AB=BC=BG,
∴∠BCG=∠BGC,
∵正六边形ABCDEF的每一个内角是4×180°÷6=120°,
正方形ABGH的每个内角是90°,
∴∠CBG=360°﹣120°﹣90°=150°,
∴∠BCG+∠BGC=180°﹣150°=30°,
∴∠BCG=15°.
答案:15°.
15.(2021?湖州)为庆祝中国共产党建党
(?http:?/??/?www.21cnjy.com?)100周年,某校用红色灯带制作了一个如图所示的正五角星(A,B,C,D,E是正五角星的五个顶点),则图中∠A的度数是
36 度.【来源:21·世纪·教育·网】
(?http:?/??/?www.21cnjy.com?)
解:如图,
(?http:?/??/?www.21cnjy.com?)
∵正五角星中,五边形FGHMN是正五边形,
∴∠GFN=∠FNM==108°,
∴∠AFN=∠ANF=180°﹣∠GFN=180°﹣108°=72°,
∴∠A=180°﹣∠AFN﹣∠ANF=180°﹣72°﹣72°=36°.
答案:36.
16.(2020?枣庄)各顶点都在方格纸的格点(横竖格子线的交错点)上的多边形称为格点多边形,它的面积S可用公式S=a+b﹣1(a是多边形内的格点数,b是多边形边界上的格点数)计算,这个公式称为“皮克(Pick)定理”.如图给出了一个格点五边形,则该五边形的面积S= 6 .21·cn·jy·com
(?http:?/??/?www.21cnjy.com?)
解:a表示多边形内部的格点数,b表示多边形边界上的格点数,S表示多边形的面积,
通过图象可知a=4,b=6,
∴该五边形的面积S=4+×6﹣1=6,
答案:6.
三、解答题
17.(2021?唐山模拟)在一个多边形中,一个内角相邻的外角与其他各内角的和为600°.
(1)如果这个多边形是五边形,请求出这个外角的度数;
(2)是否存在符合题意的其他多边形?如果存在,请求出边数及这个外角的度数;如果不存在,请说明理由.
解:
(1)设这个外角的度数是x°,则
(5﹣2)×180﹣(180﹣x)+x=600,
解得x=120.
故这个外角的度数是120°.
(2)存在.
设边数为n,这个外角的度数是x°,则
(n﹣2)×180﹣(180﹣x)+x=600,
整理得x=570﹣90n,
∵0<x<180,
即0<570﹣90n<180,并且n为正整数,
∴n=5或n=6.
故这个多边形的边数是6,这个外角的度数为30°.
18.(2021?衡水模拟
(?http:?/??/?www.21cnjy.com?))如图,在五边形ABCDE中,∠C=100°,∠D=75°,∠E=135°,AP平分∠EAB,BP平分∠ABC,求∠P的度数.【出处:21教育名师】
(?http:?/??/?www.21cnjy.com?)
解:∵∠EAB+∠ABC+∠C+∠D+∠E=540°,∠C=100°,∠D=75°,∠E=135°
∴∠EAB+∠ABC=540°﹣∠C﹣∠D﹣∠E=230°,
∵AP平分∠EAB
∴,
同理可得,,
∵∠P+∠PAB+∠PBA=180°,
∴∠P=180°﹣∠PAB﹣∠PBA====65°.
19.(2021?安徽模拟
(?http:?/??/?www.21cnjy.com?))如图,一定数量的石子可以摆成如图所示的三角形和四边形,古希腊科学家把数1,3,6,10,15,21,……称为“三角形数“;把1,4,9,16,25,……称为“正方形数“.同样,可以把数1,5,12,22,……,称为“五边形数”,www.21-cn-jy.com
(?http:?/??/?www.21cnjy.com?)
将三角形、正方形、五边形都整齐的由左到右填在所示表格里:
三角形数
1
3
6
10
15
21
a
…
正方形数
1
4
9
16
25
b
49
…
五边形数
1
5
12
22
c
51
70
…
(1)按照规律,表格中a= 28 ,b= 36 ,c= 35 ;
(2)观察表中规律,第n个“五边形数”是 .
解:(1)∵前6个“三角形数”分别是:
1=、3=、6=、10=、15=、21=,
∴第n个“三角形数”是,
∴a==28.
∵前5个“正方形数”分别是:
1=12,4=22,9=32,16=42,25=52,
∴第n个“正方形数”是n2,
∴b=62=36.
∵前4个“五边形数”分别是:
1=,5=,12=,22=,
∴c==35.
(2)根据(1)中的规律得出:第n个“五边形数”是;
答案:.
20.(2021?重庆模拟)如图,四边形ABCD中,∠A=∠C=90°,DE平分∠ADC交AB边于点E,BF平分∠ABC交DC边于点F.21教育网
求证:DE∥BF.
(?http:?/??/?www.21cnjy.com?)
证明:∵四边形ABCD中,∠A=∠C=90°,
∴∠ADC+∠ABC=180°,
∵DE平分∠ADC交AB边于点E,BF平分∠ABC交DC边于点F,
∴∠ADE=∠EDC,∠ABF=∠CBF,
∴∠ADE+∠FBC=90°,
∵∠AED+∠ADE=90°,∠ADE=∠EDC,
∴∠AED=∠ABF,
∴DE∥BF.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
