【人教版八上高频易错必刷题】12.1 全等三角形(含解析)
文档属性
| 名称 | 【人教版八上高频易错必刷题】12.1 全等三角形(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-18 18:23:34 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
12.1
全等三角形
高频易错必刷题汇编
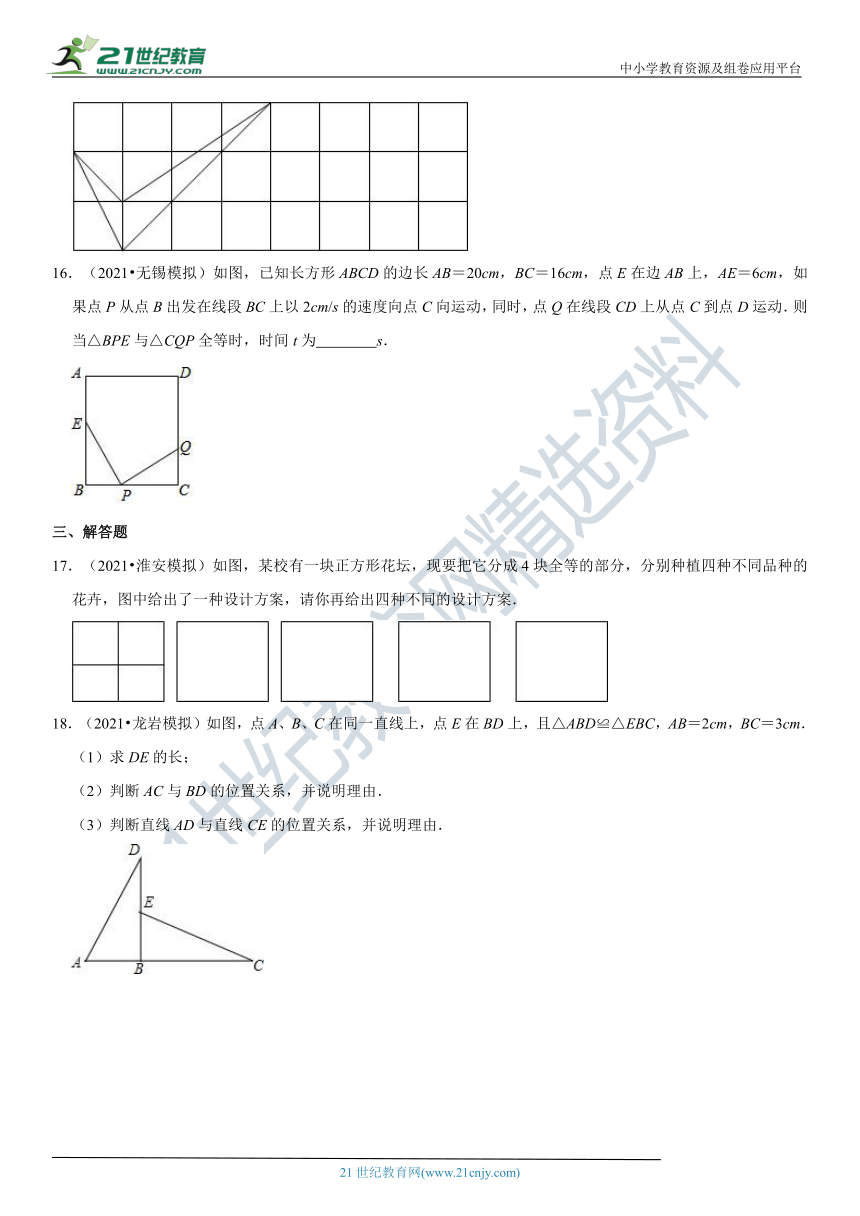
一、选择题
1.(2021?西安模拟)如图,在下列4个正方形图案中,与左边正方形图案全等的图案是( )
A.
B.
C.
D.
2.(2021?哈尔滨)如图,△A
(?http:?/??/?www.21cnjy.com?)BC≌△DEC,点A和点D是对应顶点,点B和点E是对应顶点,过点A作AF⊥CD,垂足为点F,若∠BCE=65°,则∠CAF的度数为( )21世纪教育网版权所有
(?http:?/??/?www.21cnjy.com?)
A.30°
B.25°
C.35°
D.65°
3.(2021?上海模拟)在平面直角坐
(?http:?/??/?www.21cnjy.com?)标系xOy中,点A(﹣3,0),B(2,0),C(﹣1,2),E(4,2),如果△ABC与△EFB全等,那么点F的坐标可以是( )21
cnjy
com
A.(6,0)
B.(4,0)
C.(4,﹣2)
D.(4,﹣3)
4.(2021?济南模拟)如图是由4个相同的小正方形组成的网格图,其中∠1+∠2等于( )
(?http:?/??/?www.21cnjy.com?)
A.150°
B.180°
C.210°
D.225°
5.(2021?常州模拟)如图,
(?http:?/??/?www.21cnjy.com?)△AOB≌△ADC,点B和点C是对应顶点,∠O=∠D=90°,记∠OAD=α,∠ABO=β,当BC∥OA时,α与β之间的数量关系为( )【出处:21教育名师】
(?http:?/??/?www.21cnjy.com?)
A.α=β
B.α=2β
C.α+β=90°
D.α+β=180°
6.(2021?石家庄模拟)三个全等三角形按如图的形式摆放,则∠1+∠2+∠3的度数是( )
(?http:?/??/?www.21cnjy.com?)
A.90°
B.120°
C.135°
D.180°
7.(2021?鞍山模拟
(?http:?/??/?www.21cnjy.com?))如图,两个全等的等边三角形的边长为1m,一个微型机器人由A点开始按ABCDBEA的顺序沿等边三角形的边循环运动,行走2010m停下,则这个微型机器人停在( )【版权所有:21教育】
(?http:?/??/?www.21cnjy.com?)
A.点A处
B.点B处
C.点C处
D.点E处
8.(2021?宁波模拟)如图,△ABC≌△AED,点E在线段BC上,∠1=40°,则∠AED的度数是( )
(?http:?/??/?www.21cnjy.com?)
A.70°
B.68°
C.65°
D.60°
9.(2021?南通模拟)如图,已知△ABC≌△ADE,且∠CAD=10°,∠B=∠D=25°,∠EAB=120°,则∠EGF=( )21
cnjy
com
(?http:?/??/?www.21cnjy.com?)
A.120°
B.135°
C.115°
D.125°
10.(2021?达州模拟)如图,锐角△
(?http:?/??/?www.21cnjy.com?)ABC中,D、E分别是AB、AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且C′D∥EB′∥BC,BE、CD交于点F.若∠BAC=35°,则∠BFC的大小是( )
(?http:?/??/?www.21cnjy.com?)
A.105°
B.110°
C.100°
D.120°
二、填空题
11.(2021?绵阳模拟)如图
(?http:?/??/?www.21cnjy.com?),△ABC≌△ADE,线段BC的延长线过点E,与线段AD交于点F,∠ACB=∠AED=108°,∠CAD=12°,∠B=48°,则∠DEF的度数
.
(?http:?/??/?www.21cnjy.com?)
12.(2021?上海模拟)在△
(?http:?/??/?www.21cnjy.com?)ABC和△A1B1C1中,已知∠C=∠C1=90°,AC=A1C1=3,BC=4,B1C1=2,点D、D1分别在边AB、A1B1上,且△ACD≌△C1A1D1,那么AD的长是
.
13.(2021?牡丹江
(?http:?/??/?www.21cnjy.com?)模拟)如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到△DEF的位置,AB=10,DO=4,平移距离为6,则阴影部分面积为
.
(?http:?/??/?www.21cnjy.com?)
14.(2021?四平模拟)如
(?http:?/??/?www.21cnjy.com?)图,A、C、N三点在同一直线上,在△ABC中,∠A:∠ABC:∠ACB=3:5:10,若△MNC≌△ABC,则∠BCM:∠BCN=
.
(?http:?/??/?www.21cnjy.com?)
15.(2021?盐城模拟)如
(?http:?/??/?www.21cnjy.com?)图,在由边长为1cm的小正方形组成的网格中,画如图所示的燕尾形工件,现要求最大限度的裁剪出10个与它全等的燕尾形工件,则这个网格的长至少为(接缝不计)
.
(?http:?/??/?www.21cnjy.com?)
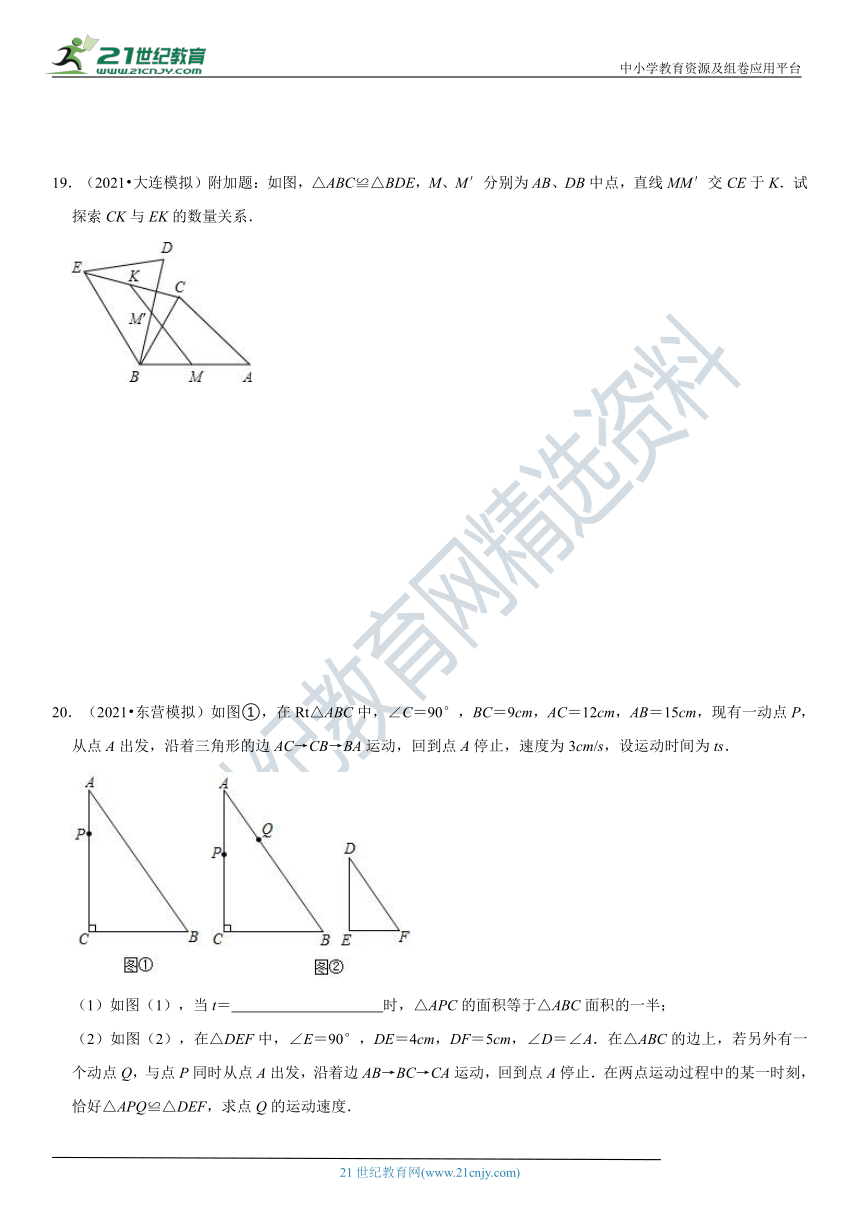
16.(2021?无锡模拟)如图,
(?http:?/??/?www.21cnjy.com?)已知长方形ABCD的边长AB=20cm,BC=16cm,点E在边AB上,AE=6cm,如果点P从点B出发在线段BC上以2cm/s的速度向点C向运动,同时,点Q在线段CD上从点C到点D运动.则当△BPE与△CQP全等时,时间t为
s.
(?http:?/??/?www.21cnjy.com?)
三、解答题
17.(2021?淮安模拟)如图,某校有
(?http:?/??/?www.21cnjy.com?)一块正方形花坛,现要把它分成4块全等的部分,分别种植四种不同品种的花卉,图中给出了一种设计方案,请你再给出四种不同的设计方案.21·cn·jy·com
(?http:?/??/?www.21cnjy.com?)
18.(2021?龙岩模拟)如图,点A、B、C在同一直线上,点E在BD上,且△ABD≌△EBC,AB=2cm,BC=3cm.
(1)求DE的长;
(2)判断AC与BD的位置关系,并说明理由.
(3)判断直线AD与直线CE的位置关系,并说明理由.
(?http:?/??/?www.21cnjy.com?)
19.(2021?大连模拟)附加
(?http:?/??/?www.21cnjy.com?)题:如图,△ABC≌△BDE,M、M′分别为AB、DB中点,直线MM′交CE于K.试探索CK与EK的数量关系.
(?http:?/??/?www.21cnjy.com?)
20.(2021?东营模拟)如图①,在
(?http:?/??/?www.21cnjy.com?)Rt△ABC中,∠C=90°,BC=9cm,AC=12cm,AB=15cm,现有一动点P,从点A出发,沿着三角形的边AC→CB→BA运动,回到点A停止,速度为3cm/s,设运动时间为ts.
(?http:?/??/?www.21cnjy.com?)
(1)如图(1),当t=
时,△APC的面积等于△ABC面积的一半;
(2)如图(2),在△DEF中,∠E=9
(?http:?/??/?www.21cnjy.com?)0°,DE=4cm,DF=5cm,∠D=∠A.在△ABC的边上,若另外有一个动点Q,与点P同时从点A出发,沿着边AB→BC→CA运动,回到点A停止.在两点运动过程中的某一时刻,恰好△APQ≌△DEF,求点Q的运动速度.2-1-c-n-j-y
12.1
全等三角形
高频易错必刷题汇编
一、选择题
1.(2021?西安模拟)如图,在下列4个正方形图案中,与左边正方形图案全等的图案是( )
A.
B.
C.
D.
解:能够完全重合的两个图形叫做全等形.
A、B、D图案均与题干中的图形不重合,所以不属于全等的图案,
C中的图案旋转180°后与题干中的图形重合.
答案:C.
2.(2021?哈尔滨)如图
(?http:?/??/?www.21cnjy.com?),△ABC≌△DEC,点A和点D是对应顶点,点B和点E是对应顶点,过点A作AF⊥CD,垂足为点F,若∠BCE=65°,则∠CAF的度数为( )
(?http:?/??/?www.21cnjy.com?)
A.30°
B.25°
C.35°
D.65°
解:∵△ABC≌△DEC,
∴∠ACB=∠DCE,
∵∠BCE=65°,
∴∠ACD=∠BCE=65°,
∵AF⊥CD,
∴∠AFC=90°,
∴∠CAF+∠ACD=90°,
∴∠CAF=90°﹣65°=25°,
答案:B.
3.(2021?上海模拟
(?http:?/??/?www.21cnjy.com?))在平面直角坐标系xOy中,点A(﹣3,0),B(2,0),C(﹣1,2),E(4,2),如果△ABC与△EFB全等,那么点F的坐标可以是( )
A.(6,0)
B.(4,0)
C.(4,﹣2)
D.(4,﹣3)
解:如图所示:△ABC与△EFB全等,点F的坐标可以是:(4,﹣3).
答案:D.
(?http:?/??/?www.21cnjy.com?)
4.(2021?济南模拟)如图是由4个相同的小正方形组成的网格图,其中∠1+∠2等于( )
(?http:?/??/?www.21cnjy.com?)
A.150°
B.180°
C.210°
D.225°
解:
由题意得:AB=ED,BC=DC,∠D=∠B=90°,
∴△ABC≌△EDC(SAS),
∴∠BAC=∠1,
∠1+∠2=180°.
答案:B.
(?http:?/??/?www.21cnjy.com?)
5.(2021?常州模拟)如图,△AOB
(?http:?/??/?www.21cnjy.com?)≌△ADC,点B和点C是对应顶点,∠O=∠D=90°,记∠OAD=α,∠ABO=β,当BC∥OA时,α与β之间的数量关系为( )www.21-cn-jy.com
(?http:?/??/?www.21cnjy.com?)
A.α=β
B.α=2β
C.α+β=90°
D.α+β=180°
解:∵△AOB≌△ADC,
∴AB=AC,∠BAO=∠CAD,
∴∠BAC=∠OAD=α,
在△ABC中,∠ABC=(180°﹣α),
∵BC∥OA,
∴∠OBC=180°﹣∠O=180°﹣90°=90°,
∴β+(180°﹣α)=90°,
整理得,α=2β.
答案:B.
6.(2021?石家庄模拟)三个全等三角形按如图的形式摆放,则∠1+∠2+∠3的度数是( )
(?http:?/??/?www.21cnjy.com?)
A.90°
B.120°
C.135°
D.180°
解:如图所示:
由图形可得:∠1+∠4+∠5+∠8+∠6+∠2+∠3+∠9+∠7=540°,
∵三个全等三角形,
∴∠4+∠9+∠6=180°,
又∵∠5+∠7+∠8=180°,
∴∠1+∠2+∠3+180°+180°=540°,
∴∠1+∠2+∠3的度数是180°.
答案:D.
(?http:?/??/?www.21cnjy.com?)
7.(2021?鞍山模拟)如图,两个全
(?http:?/??/?www.21cnjy.com?)等的等边三角形的边长为1m,一个微型机器人由A点开始按ABCDBEA的顺序沿等边三角形的边循环运动,行走2010m停下,则这个微型机器人停在( )www-2-1-cnjy-com
(?http:?/??/?www.21cnjy.com?)
A.点A处
B.点B处
C.点C处
D.点E处
解:∵两个全等的等边三角形的边长为1m,
∴机器人由A点开始按ABCDBEA的顺序沿等边三角形的边循环运动一圈,即为6m,
∵2010÷6=335,即正好行走了335圈,回到出发点,
∴行走2010m停下,则这个微型机器人停在A点.
答案:A.
8.(2021?宁波模拟)如图,△ABC≌△AED,点E在线段BC上,∠1=40°,则∠AED的度数是( )
(?http:?/??/?www.21cnjy.com?)
A.70°
B.68°
C.65°
D.60°
解:∵△ABC≌△AED,
∴∠AED=∠B,AE=AB,∠BAC=∠EAD,
∴∠1=∠BAE=40°,
∴△ABE中,∠B==70°,
∴∠AED=70°,
答案:A.
9.(2021?南通模拟)如图,已知△ABC≌△ADE,且∠CAD=10°,∠B=∠D=25°,∠EAB=120°,则∠EGF=( )2·1·c·n·j·y
(?http:?/??/?www.21cnjy.com?)
A.120°
B.135°
C.115°
D.125°
解:∵△ABC≌△ADE,∠CAD=10°,∠EAB=120°,
∴∠EAD=∠CAB=(∠EAB﹣∠CAD)=55°,
∵∠FAB=∠CAD+∠CAB,
∴∠FAB=65°,
∵∠AFB+∠FAB+∠B=180°,
∴∠AFB=180°﹣65°﹣25°=90°,
∵∠GFD=∠AFB,
∴∠GFD=90°,
∵∠EGF=∠D+∠GFD,
∴∠EGF=90°+25°=115°.
答案:C.
10.(2021?达州模拟)如图,锐角
(?http:?/??/?www.21cnjy.com?)△ABC中,D、E分别是AB、AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且C′D∥EB′∥BC,BE、CD交于点F.若∠BAC=35°,则∠BFC的大小是( )
(?http:?/??/?www.21cnjy.com?)
A.105°
B.110°
C.100°
D.120°
解:设∠C′=α,∠B′=β,
∵△ADC≌△ADC′,△AEB≌△AEB′,
∴∠ACD=∠C′=α,∠ABE=∠B′=β,∠BAE=∠B′AE=35°,
∴∠C′DB=∠BAC′+AC′D=35°+α,∠CEB′=35°+β.
∵C′D∥EB′∥BC,
∴∠ABC=∠C′DB=35°+α,∠ACB=∠CEB′=35°+β,
∴∠BAC+∠ABC+∠ACB=180°,即105°+α+β=180°.
则α+β=75°.
∵∠BFC=∠BDC+∠DBE,
∴∠BFC=35°+α+β=35°+75°=110°.
答案:B.
(?http:?/??/?www.21cnjy.com?)
二、填空题
11.(2021?绵阳模拟)如图
(?http:?/??/?www.21cnjy.com?),△ABC≌△ADE,线段BC的延长线过点E,与线段AD交于点F,∠ACB=∠AED=108°,∠CAD=12°,∠B=48°,则∠DEF的度数 36° .21·世纪
教育网
(?http:?/??/?www.21cnjy.com?)
解:∵∠ACB=108°,∠B=48°,
∴∠CAB=180°﹣∠B﹣∠ACB=180°﹣48°﹣108°=24°.
又∵△ABC≌△ADE,
∴∠EAD=∠CAB=24°.
又∵∠EAB=∠EAD+∠CAD+∠CAB,∠CAD=12°,
∴∠EAB=24°+12°+24°=60°,
∴∠AEB=180°﹣∠EAB﹣∠B=180°﹣60°﹣48°=72°,
∴∠DEF=∠AED﹣∠AEB=108°﹣72°=36°.
答案:36°
12.(2021?上海模拟)在△ABC和△A1B1C1中,已知∠C=∠C1=90°,AC=A1C1=3,BC=4,B1C1=2,点D、D1分别在边AB、A1B1上,且△ACD≌△C1A1D1,那么AD的长是 .21教育名师原创作品
解:∵△ACD≌△C1A1D1,可以将△C1A1D1与△ACD重合,如图,
∵∠ACB=∠A1C1B1=90°,
∴BC∥B1C1,
∴=,
∵AC=3,BC=4,
∴AB==5,
∴=,
解得AD=,
∴AD的长为,
答案:.
(?http:?/??/?www.21cnjy.com?)
13.(2021?牡丹江模
(?http:?/??/?www.21cnjy.com?)拟)如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到△DEF的位置,AB=10,DO=4,平移距离为6,则阴影部分面积为 48 .21cnjy.com
(?http:?/??/?www.21cnjy.com?)
解:由平移的性质知,BE=6,DE=AB=10,
∴OE=DE﹣DO=10﹣4=6,
∴S四边形ODFC=S梯形ABEO=(AB+OE)?BE=(10+6)×6=48.
答案:48.
14.(2021?四平模拟)如图,
(?http:?/??/?www.21cnjy.com?)A、C、N三点在同一直线上,在△ABC中,∠A:∠ABC:∠ACB=3:5:10,若△MNC≌△ABC,则∠BCM:∠BCN= 1:4 .
(?http:?/??/?www.21cnjy.com?)
解:∵∠A:∠ABC:∠ACB=3:5:10,∠A+∠ABC+∠ACB=180°,
∴∠A=30°,∠ABC=50°,∠ACB=100°,
∵△MNC≌△ABC,
∴∠N=∠ABC=50°,∠M=∠A=30°,
∴∠MCA=∠M+∠N=80°,
∴∠BCM=20°,∠BCN=80°,
∴∠BCM:∠BCN=1:4,
答案:1:4.
15.(2021?盐城模拟)
(?http:?/??/?www.21cnjy.com?)如图,在由边长为1cm的小正方形组成的网格中,画如图所示的燕尾形工件,现要求最大限度的裁剪出10个与它全等的燕尾形工件,则这个网格的长至少为(接缝不计) 21 .
(?http:?/??/?www.21cnjy.com?)
解:∵后面画出的图形与第一个图形完全一样
(?http:?/??/?www.21cnjy.com?)
∴画第二个图形的时候,需往右用1个格,画第三个图的时候,需要再往右用三个格,画第四个图的时候,需要再往右走1个格…【来源:21cnj
y.co
m】
∴画第10个图时,网格的长为4+(1+3+1+3+1+3+1+3+1)=21个.
16.(2021?无锡模拟)如图,已知
(?http:?/??/?www.21cnjy.com?)长方形ABCD的边长AB=20cm,BC=16cm,点E在边AB上,AE=6cm,如果点P从点B出发在线段BC上以2cm/s的速度向点C向运动,同时,点Q在线段CD上从点C到点D运动.则当△BPE与△CQP全等时,时间t为 1或4 s.
(?http:?/??/?www.21cnjy.com?)
解:
∵AB=20cm,AE=6cm,BC=16cm,
∴BE=14cm,BP=2tcm,PC=(16﹣2t)cm,
当△BPE≌△CQP时,则有BE=PC,即14=16﹣2t,解得t=1,
当△BPE≌△CPQ时,则有BP=PC,即2t=16﹣2t,解得t=4,
答案:1或4.
三、解答题
17.(2021?淮安模拟)如图,某校有一
(?http:?/??/?www.21cnjy.com?)块正方形花坛,现要把它分成4块全等的部分,分别种植四种不同品种的花卉,图中给出了一种设计方案,请你再给出四种不同的设计方案.
(?http:?/??/?www.21cnjy.com?)
解:设计方案如下:
(?http:?/??/?www.21cnjy.com?)
18.(2021?龙岩模拟)如图,点A、B、C在同一直线上,点E在BD上,且△ABD≌△EBC,AB=2cm,BC=3cm.
(1)求DE的长;
(2)判断AC与BD的位置关系,并说明理由.
(3)判断直线AD与直线CE的位置关系,并说明理由.
(?http:?/??/?www.21cnjy.com?)
解:(1)∵△ABD≌△EBC,
∴BD=BC=3cm,BE=AB=2cm,
∴DE=BD﹣BE=1cm;
(2)DB与AC垂直,
理由:∵△ABD≌△EBC,
∴∠ABD=∠EBC,
又A、B、C在一条直线上,
∴∠EBC=90°,
∴DB与AC垂直.
(3)直线AD与直线CE垂直.
理由:如图,延长CE交AD于F,
(?http:?/??/?www.21cnjy.com?)
∵△ABD≌△EBC,
∴∠D=∠C,
∵Rt△ABD中,∠A+∠D=90°,
∴∠A+∠C=90°,
∴∠AFC=90°,即CE⊥AD.
19.(2021?大连模
(?http:?/??/?www.21cnjy.com?)拟)附加题:如图,△ABC≌△BDE,M、M′分别为AB、DB中点,直线MM′交CE于K.试探索CK与EK的数量关系.21教育网
(?http:?/??/?www.21cnjy.com?)
解:CK与EK的数量关系为相等,理由如下:
延长MK到N,使得NK=MM',连接EM′、CM、EN,如图,
可得NK+KM'=MM'+M'K,即NM'=MK,
∵△ABC≌△BDE,M、M′分别为AB、DB中点,
∴EM'=CM,BM'=BM,∠EM'D=∠CMB,
由BM'=BM得:∠BM'M=∠BMM'=∠KM'D,
∴∠NM'E=∠CMK,
在△EM'N和△CMK中,
,
∴△EM'N≌△CMK,(SAS)
∴CK=EN,∠N=∠CKM=∠NKE,
∴EK=EN,
∴CK=EK.
(?http:?/??/?www.21cnjy.com?)
20.(2021?东营模拟)如图①,在Rt△
(?http:?/??/?www.21cnjy.com?)ABC中,∠C=90°,BC=9cm,AC=12cm,AB=15cm,现有一动点P,从点A出发,沿着三角形的边AC→CB→BA运动,回到点A停止,速度为3cm/s,设运动时间为ts.
(?http:?/??/?www.21cnjy.com?)
(1)如图(1),当t= 或 时,△APC的面积等于△ABC面积的一半;
(2)如图(2),在△DEF中
(?http:?/??/?www.21cnjy.com?),∠E=90°,DE=4cm,DF=5cm,∠D=∠A.在△ABC的边上,若另外有一个动点Q,与点P同时从点A出发,沿着边AB→BC→CA运动,回到点A停止.在两点运动过程中的某一时刻,恰好△APQ≌△DEF,求点Q的运动速度.【来源:21·世纪·教育·网】
解:(1)①当点P在BC上时,如图①﹣1,
若△APC的面积等于△ABC面积的一半;则CP=BC=cm,
此时,点P移动的距离为AC+CP=12+=,
移动的时间为:÷3=秒,
②当点P在BA上时,如图①﹣2
若△APC的面积等于△ABC面积的一半;则PD=BC,即点P为BA中点,
此时,点P移动的距离为AC+CB+BP=12+9+=cm,
移动的时间为:÷3=秒,
答案:或;
(2)△APQ≌△DEF,即,对应顶点为A与D,P与E,Q与F;
①当点P在AC上,如图②﹣1所示:
此时,AP=4,AQ=5,
∴点Q移动的速度为5÷(4÷3)=cm/s,
②当点P在AB上,如图②﹣2所示:
此时,AP=4,AQ=5,
即,点P移动的距离为9+12+15﹣4=32cm,点Q移动的距离为9+12+15﹣5=31cm,
∴点Q移动的速度为31÷(32÷3)=cm/s,
综上所述,两点运动过程中的某一时刻,恰好△APQ≌△DEF,
点Q的运动速为cm/s或cm/s.
(?http:?/??/?www.21cnjy.com?)
(?http:?/??/?www.21cnjy.com?)
(?http:?/??/?www.21cnjy.com?)
(?http:?/??/?www.21cnjy.com?)
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
12.1
全等三角形
高频易错必刷题汇编
一、选择题
1.(2021?西安模拟)如图,在下列4个正方形图案中,与左边正方形图案全等的图案是( )
A.
B.
C.
D.
2.(2021?哈尔滨)如图,△A
(?http:?/??/?www.21cnjy.com?)BC≌△DEC,点A和点D是对应顶点,点B和点E是对应顶点,过点A作AF⊥CD,垂足为点F,若∠BCE=65°,则∠CAF的度数为( )21世纪教育网版权所有
(?http:?/??/?www.21cnjy.com?)
A.30°
B.25°
C.35°
D.65°
3.(2021?上海模拟)在平面直角坐
(?http:?/??/?www.21cnjy.com?)标系xOy中,点A(﹣3,0),B(2,0),C(﹣1,2),E(4,2),如果△ABC与△EFB全等,那么点F的坐标可以是( )21
cnjy
com
A.(6,0)
B.(4,0)
C.(4,﹣2)
D.(4,﹣3)
4.(2021?济南模拟)如图是由4个相同的小正方形组成的网格图,其中∠1+∠2等于( )
(?http:?/??/?www.21cnjy.com?)
A.150°
B.180°
C.210°
D.225°
5.(2021?常州模拟)如图,
(?http:?/??/?www.21cnjy.com?)△AOB≌△ADC,点B和点C是对应顶点,∠O=∠D=90°,记∠OAD=α,∠ABO=β,当BC∥OA时,α与β之间的数量关系为( )【出处:21教育名师】
(?http:?/??/?www.21cnjy.com?)
A.α=β
B.α=2β
C.α+β=90°
D.α+β=180°
6.(2021?石家庄模拟)三个全等三角形按如图的形式摆放,则∠1+∠2+∠3的度数是( )
(?http:?/??/?www.21cnjy.com?)
A.90°
B.120°
C.135°
D.180°
7.(2021?鞍山模拟
(?http:?/??/?www.21cnjy.com?))如图,两个全等的等边三角形的边长为1m,一个微型机器人由A点开始按ABCDBEA的顺序沿等边三角形的边循环运动,行走2010m停下,则这个微型机器人停在( )【版权所有:21教育】
(?http:?/??/?www.21cnjy.com?)
A.点A处
B.点B处
C.点C处
D.点E处
8.(2021?宁波模拟)如图,△ABC≌△AED,点E在线段BC上,∠1=40°,则∠AED的度数是( )
(?http:?/??/?www.21cnjy.com?)
A.70°
B.68°
C.65°
D.60°
9.(2021?南通模拟)如图,已知△ABC≌△ADE,且∠CAD=10°,∠B=∠D=25°,∠EAB=120°,则∠EGF=( )21
cnjy
com
(?http:?/??/?www.21cnjy.com?)
A.120°
B.135°
C.115°
D.125°
10.(2021?达州模拟)如图,锐角△
(?http:?/??/?www.21cnjy.com?)ABC中,D、E分别是AB、AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且C′D∥EB′∥BC,BE、CD交于点F.若∠BAC=35°,则∠BFC的大小是( )
(?http:?/??/?www.21cnjy.com?)
A.105°
B.110°
C.100°
D.120°
二、填空题
11.(2021?绵阳模拟)如图
(?http:?/??/?www.21cnjy.com?),△ABC≌△ADE,线段BC的延长线过点E,与线段AD交于点F,∠ACB=∠AED=108°,∠CAD=12°,∠B=48°,则∠DEF的度数
.
(?http:?/??/?www.21cnjy.com?)
12.(2021?上海模拟)在△
(?http:?/??/?www.21cnjy.com?)ABC和△A1B1C1中,已知∠C=∠C1=90°,AC=A1C1=3,BC=4,B1C1=2,点D、D1分别在边AB、A1B1上,且△ACD≌△C1A1D1,那么AD的长是
.
13.(2021?牡丹江
(?http:?/??/?www.21cnjy.com?)模拟)如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到△DEF的位置,AB=10,DO=4,平移距离为6,则阴影部分面积为
.
(?http:?/??/?www.21cnjy.com?)
14.(2021?四平模拟)如
(?http:?/??/?www.21cnjy.com?)图,A、C、N三点在同一直线上,在△ABC中,∠A:∠ABC:∠ACB=3:5:10,若△MNC≌△ABC,则∠BCM:∠BCN=
.
(?http:?/??/?www.21cnjy.com?)
15.(2021?盐城模拟)如
(?http:?/??/?www.21cnjy.com?)图,在由边长为1cm的小正方形组成的网格中,画如图所示的燕尾形工件,现要求最大限度的裁剪出10个与它全等的燕尾形工件,则这个网格的长至少为(接缝不计)
.
(?http:?/??/?www.21cnjy.com?)
16.(2021?无锡模拟)如图,
(?http:?/??/?www.21cnjy.com?)已知长方形ABCD的边长AB=20cm,BC=16cm,点E在边AB上,AE=6cm,如果点P从点B出发在线段BC上以2cm/s的速度向点C向运动,同时,点Q在线段CD上从点C到点D运动.则当△BPE与△CQP全等时,时间t为
s.
(?http:?/??/?www.21cnjy.com?)
三、解答题
17.(2021?淮安模拟)如图,某校有
(?http:?/??/?www.21cnjy.com?)一块正方形花坛,现要把它分成4块全等的部分,分别种植四种不同品种的花卉,图中给出了一种设计方案,请你再给出四种不同的设计方案.21·cn·jy·com
(?http:?/??/?www.21cnjy.com?)
18.(2021?龙岩模拟)如图,点A、B、C在同一直线上,点E在BD上,且△ABD≌△EBC,AB=2cm,BC=3cm.
(1)求DE的长;
(2)判断AC与BD的位置关系,并说明理由.
(3)判断直线AD与直线CE的位置关系,并说明理由.
(?http:?/??/?www.21cnjy.com?)
19.(2021?大连模拟)附加
(?http:?/??/?www.21cnjy.com?)题:如图,△ABC≌△BDE,M、M′分别为AB、DB中点,直线MM′交CE于K.试探索CK与EK的数量关系.
(?http:?/??/?www.21cnjy.com?)
20.(2021?东营模拟)如图①,在
(?http:?/??/?www.21cnjy.com?)Rt△ABC中,∠C=90°,BC=9cm,AC=12cm,AB=15cm,现有一动点P,从点A出发,沿着三角形的边AC→CB→BA运动,回到点A停止,速度为3cm/s,设运动时间为ts.
(?http:?/??/?www.21cnjy.com?)
(1)如图(1),当t=
时,△APC的面积等于△ABC面积的一半;
(2)如图(2),在△DEF中,∠E=9
(?http:?/??/?www.21cnjy.com?)0°,DE=4cm,DF=5cm,∠D=∠A.在△ABC的边上,若另外有一个动点Q,与点P同时从点A出发,沿着边AB→BC→CA运动,回到点A停止.在两点运动过程中的某一时刻,恰好△APQ≌△DEF,求点Q的运动速度.2-1-c-n-j-y
12.1
全等三角形
高频易错必刷题汇编
一、选择题
1.(2021?西安模拟)如图,在下列4个正方形图案中,与左边正方形图案全等的图案是( )
A.
B.
C.
D.
解:能够完全重合的两个图形叫做全等形.
A、B、D图案均与题干中的图形不重合,所以不属于全等的图案,
C中的图案旋转180°后与题干中的图形重合.
答案:C.
2.(2021?哈尔滨)如图
(?http:?/??/?www.21cnjy.com?),△ABC≌△DEC,点A和点D是对应顶点,点B和点E是对应顶点,过点A作AF⊥CD,垂足为点F,若∠BCE=65°,则∠CAF的度数为( )
(?http:?/??/?www.21cnjy.com?)
A.30°
B.25°
C.35°
D.65°
解:∵△ABC≌△DEC,
∴∠ACB=∠DCE,
∵∠BCE=65°,
∴∠ACD=∠BCE=65°,
∵AF⊥CD,
∴∠AFC=90°,
∴∠CAF+∠ACD=90°,
∴∠CAF=90°﹣65°=25°,
答案:B.
3.(2021?上海模拟
(?http:?/??/?www.21cnjy.com?))在平面直角坐标系xOy中,点A(﹣3,0),B(2,0),C(﹣1,2),E(4,2),如果△ABC与△EFB全等,那么点F的坐标可以是( )
A.(6,0)
B.(4,0)
C.(4,﹣2)
D.(4,﹣3)
解:如图所示:△ABC与△EFB全等,点F的坐标可以是:(4,﹣3).
答案:D.
(?http:?/??/?www.21cnjy.com?)
4.(2021?济南模拟)如图是由4个相同的小正方形组成的网格图,其中∠1+∠2等于( )
(?http:?/??/?www.21cnjy.com?)
A.150°
B.180°
C.210°
D.225°
解:
由题意得:AB=ED,BC=DC,∠D=∠B=90°,
∴△ABC≌△EDC(SAS),
∴∠BAC=∠1,
∠1+∠2=180°.
答案:B.
(?http:?/??/?www.21cnjy.com?)
5.(2021?常州模拟)如图,△AOB
(?http:?/??/?www.21cnjy.com?)≌△ADC,点B和点C是对应顶点,∠O=∠D=90°,记∠OAD=α,∠ABO=β,当BC∥OA时,α与β之间的数量关系为( )www.21-cn-jy.com
(?http:?/??/?www.21cnjy.com?)
A.α=β
B.α=2β
C.α+β=90°
D.α+β=180°
解:∵△AOB≌△ADC,
∴AB=AC,∠BAO=∠CAD,
∴∠BAC=∠OAD=α,
在△ABC中,∠ABC=(180°﹣α),
∵BC∥OA,
∴∠OBC=180°﹣∠O=180°﹣90°=90°,
∴β+(180°﹣α)=90°,
整理得,α=2β.
答案:B.
6.(2021?石家庄模拟)三个全等三角形按如图的形式摆放,则∠1+∠2+∠3的度数是( )
(?http:?/??/?www.21cnjy.com?)
A.90°
B.120°
C.135°
D.180°
解:如图所示:
由图形可得:∠1+∠4+∠5+∠8+∠6+∠2+∠3+∠9+∠7=540°,
∵三个全等三角形,
∴∠4+∠9+∠6=180°,
又∵∠5+∠7+∠8=180°,
∴∠1+∠2+∠3+180°+180°=540°,
∴∠1+∠2+∠3的度数是180°.
答案:D.
(?http:?/??/?www.21cnjy.com?)
7.(2021?鞍山模拟)如图,两个全
(?http:?/??/?www.21cnjy.com?)等的等边三角形的边长为1m,一个微型机器人由A点开始按ABCDBEA的顺序沿等边三角形的边循环运动,行走2010m停下,则这个微型机器人停在( )www-2-1-cnjy-com
(?http:?/??/?www.21cnjy.com?)
A.点A处
B.点B处
C.点C处
D.点E处
解:∵两个全等的等边三角形的边长为1m,
∴机器人由A点开始按ABCDBEA的顺序沿等边三角形的边循环运动一圈,即为6m,
∵2010÷6=335,即正好行走了335圈,回到出发点,
∴行走2010m停下,则这个微型机器人停在A点.
答案:A.
8.(2021?宁波模拟)如图,△ABC≌△AED,点E在线段BC上,∠1=40°,则∠AED的度数是( )
(?http:?/??/?www.21cnjy.com?)
A.70°
B.68°
C.65°
D.60°
解:∵△ABC≌△AED,
∴∠AED=∠B,AE=AB,∠BAC=∠EAD,
∴∠1=∠BAE=40°,
∴△ABE中,∠B==70°,
∴∠AED=70°,
答案:A.
9.(2021?南通模拟)如图,已知△ABC≌△ADE,且∠CAD=10°,∠B=∠D=25°,∠EAB=120°,则∠EGF=( )2·1·c·n·j·y
(?http:?/??/?www.21cnjy.com?)
A.120°
B.135°
C.115°
D.125°
解:∵△ABC≌△ADE,∠CAD=10°,∠EAB=120°,
∴∠EAD=∠CAB=(∠EAB﹣∠CAD)=55°,
∵∠FAB=∠CAD+∠CAB,
∴∠FAB=65°,
∵∠AFB+∠FAB+∠B=180°,
∴∠AFB=180°﹣65°﹣25°=90°,
∵∠GFD=∠AFB,
∴∠GFD=90°,
∵∠EGF=∠D+∠GFD,
∴∠EGF=90°+25°=115°.
答案:C.
10.(2021?达州模拟)如图,锐角
(?http:?/??/?www.21cnjy.com?)△ABC中,D、E分别是AB、AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且C′D∥EB′∥BC,BE、CD交于点F.若∠BAC=35°,则∠BFC的大小是( )
(?http:?/??/?www.21cnjy.com?)
A.105°
B.110°
C.100°
D.120°
解:设∠C′=α,∠B′=β,
∵△ADC≌△ADC′,△AEB≌△AEB′,
∴∠ACD=∠C′=α,∠ABE=∠B′=β,∠BAE=∠B′AE=35°,
∴∠C′DB=∠BAC′+AC′D=35°+α,∠CEB′=35°+β.
∵C′D∥EB′∥BC,
∴∠ABC=∠C′DB=35°+α,∠ACB=∠CEB′=35°+β,
∴∠BAC+∠ABC+∠ACB=180°,即105°+α+β=180°.
则α+β=75°.
∵∠BFC=∠BDC+∠DBE,
∴∠BFC=35°+α+β=35°+75°=110°.
答案:B.
(?http:?/??/?www.21cnjy.com?)
二、填空题
11.(2021?绵阳模拟)如图
(?http:?/??/?www.21cnjy.com?),△ABC≌△ADE,线段BC的延长线过点E,与线段AD交于点F,∠ACB=∠AED=108°,∠CAD=12°,∠B=48°,则∠DEF的度数 36° .21·世纪
教育网
(?http:?/??/?www.21cnjy.com?)
解:∵∠ACB=108°,∠B=48°,
∴∠CAB=180°﹣∠B﹣∠ACB=180°﹣48°﹣108°=24°.
又∵△ABC≌△ADE,
∴∠EAD=∠CAB=24°.
又∵∠EAB=∠EAD+∠CAD+∠CAB,∠CAD=12°,
∴∠EAB=24°+12°+24°=60°,
∴∠AEB=180°﹣∠EAB﹣∠B=180°﹣60°﹣48°=72°,
∴∠DEF=∠AED﹣∠AEB=108°﹣72°=36°.
答案:36°
12.(2021?上海模拟)在△ABC和△A1B1C1中,已知∠C=∠C1=90°,AC=A1C1=3,BC=4,B1C1=2,点D、D1分别在边AB、A1B1上,且△ACD≌△C1A1D1,那么AD的长是 .21教育名师原创作品
解:∵△ACD≌△C1A1D1,可以将△C1A1D1与△ACD重合,如图,
∵∠ACB=∠A1C1B1=90°,
∴BC∥B1C1,
∴=,
∵AC=3,BC=4,
∴AB==5,
∴=,
解得AD=,
∴AD的长为,
答案:.
(?http:?/??/?www.21cnjy.com?)
13.(2021?牡丹江模
(?http:?/??/?www.21cnjy.com?)拟)如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到△DEF的位置,AB=10,DO=4,平移距离为6,则阴影部分面积为 48 .21cnjy.com
(?http:?/??/?www.21cnjy.com?)
解:由平移的性质知,BE=6,DE=AB=10,
∴OE=DE﹣DO=10﹣4=6,
∴S四边形ODFC=S梯形ABEO=(AB+OE)?BE=(10+6)×6=48.
答案:48.
14.(2021?四平模拟)如图,
(?http:?/??/?www.21cnjy.com?)A、C、N三点在同一直线上,在△ABC中,∠A:∠ABC:∠ACB=3:5:10,若△MNC≌△ABC,则∠BCM:∠BCN= 1:4 .
(?http:?/??/?www.21cnjy.com?)
解:∵∠A:∠ABC:∠ACB=3:5:10,∠A+∠ABC+∠ACB=180°,
∴∠A=30°,∠ABC=50°,∠ACB=100°,
∵△MNC≌△ABC,
∴∠N=∠ABC=50°,∠M=∠A=30°,
∴∠MCA=∠M+∠N=80°,
∴∠BCM=20°,∠BCN=80°,
∴∠BCM:∠BCN=1:4,
答案:1:4.
15.(2021?盐城模拟)
(?http:?/??/?www.21cnjy.com?)如图,在由边长为1cm的小正方形组成的网格中,画如图所示的燕尾形工件,现要求最大限度的裁剪出10个与它全等的燕尾形工件,则这个网格的长至少为(接缝不计) 21 .
(?http:?/??/?www.21cnjy.com?)
解:∵后面画出的图形与第一个图形完全一样
(?http:?/??/?www.21cnjy.com?)
∴画第二个图形的时候,需往右用1个格,画第三个图的时候,需要再往右用三个格,画第四个图的时候,需要再往右走1个格…【来源:21cnj
y.co
m】
∴画第10个图时,网格的长为4+(1+3+1+3+1+3+1+3+1)=21个.
16.(2021?无锡模拟)如图,已知
(?http:?/??/?www.21cnjy.com?)长方形ABCD的边长AB=20cm,BC=16cm,点E在边AB上,AE=6cm,如果点P从点B出发在线段BC上以2cm/s的速度向点C向运动,同时,点Q在线段CD上从点C到点D运动.则当△BPE与△CQP全等时,时间t为 1或4 s.
(?http:?/??/?www.21cnjy.com?)
解:
∵AB=20cm,AE=6cm,BC=16cm,
∴BE=14cm,BP=2tcm,PC=(16﹣2t)cm,
当△BPE≌△CQP时,则有BE=PC,即14=16﹣2t,解得t=1,
当△BPE≌△CPQ时,则有BP=PC,即2t=16﹣2t,解得t=4,
答案:1或4.
三、解答题
17.(2021?淮安模拟)如图,某校有一
(?http:?/??/?www.21cnjy.com?)块正方形花坛,现要把它分成4块全等的部分,分别种植四种不同品种的花卉,图中给出了一种设计方案,请你再给出四种不同的设计方案.
(?http:?/??/?www.21cnjy.com?)
解:设计方案如下:
(?http:?/??/?www.21cnjy.com?)
18.(2021?龙岩模拟)如图,点A、B、C在同一直线上,点E在BD上,且△ABD≌△EBC,AB=2cm,BC=3cm.
(1)求DE的长;
(2)判断AC与BD的位置关系,并说明理由.
(3)判断直线AD与直线CE的位置关系,并说明理由.
(?http:?/??/?www.21cnjy.com?)
解:(1)∵△ABD≌△EBC,
∴BD=BC=3cm,BE=AB=2cm,
∴DE=BD﹣BE=1cm;
(2)DB与AC垂直,
理由:∵△ABD≌△EBC,
∴∠ABD=∠EBC,
又A、B、C在一条直线上,
∴∠EBC=90°,
∴DB与AC垂直.
(3)直线AD与直线CE垂直.
理由:如图,延长CE交AD于F,
(?http:?/??/?www.21cnjy.com?)
∵△ABD≌△EBC,
∴∠D=∠C,
∵Rt△ABD中,∠A+∠D=90°,
∴∠A+∠C=90°,
∴∠AFC=90°,即CE⊥AD.
19.(2021?大连模
(?http:?/??/?www.21cnjy.com?)拟)附加题:如图,△ABC≌△BDE,M、M′分别为AB、DB中点,直线MM′交CE于K.试探索CK与EK的数量关系.21教育网
(?http:?/??/?www.21cnjy.com?)
解:CK与EK的数量关系为相等,理由如下:
延长MK到N,使得NK=MM',连接EM′、CM、EN,如图,
可得NK+KM'=MM'+M'K,即NM'=MK,
∵△ABC≌△BDE,M、M′分别为AB、DB中点,
∴EM'=CM,BM'=BM,∠EM'D=∠CMB,
由BM'=BM得:∠BM'M=∠BMM'=∠KM'D,
∴∠NM'E=∠CMK,
在△EM'N和△CMK中,
,
∴△EM'N≌△CMK,(SAS)
∴CK=EN,∠N=∠CKM=∠NKE,
∴EK=EN,
∴CK=EK.
(?http:?/??/?www.21cnjy.com?)
20.(2021?东营模拟)如图①,在Rt△
(?http:?/??/?www.21cnjy.com?)ABC中,∠C=90°,BC=9cm,AC=12cm,AB=15cm,现有一动点P,从点A出发,沿着三角形的边AC→CB→BA运动,回到点A停止,速度为3cm/s,设运动时间为ts.
(?http:?/??/?www.21cnjy.com?)
(1)如图(1),当t= 或 时,△APC的面积等于△ABC面积的一半;
(2)如图(2),在△DEF中
(?http:?/??/?www.21cnjy.com?),∠E=90°,DE=4cm,DF=5cm,∠D=∠A.在△ABC的边上,若另外有一个动点Q,与点P同时从点A出发,沿着边AB→BC→CA运动,回到点A停止.在两点运动过程中的某一时刻,恰好△APQ≌△DEF,求点Q的运动速度.【来源:21·世纪·教育·网】
解:(1)①当点P在BC上时,如图①﹣1,
若△APC的面积等于△ABC面积的一半;则CP=BC=cm,
此时,点P移动的距离为AC+CP=12+=,
移动的时间为:÷3=秒,
②当点P在BA上时,如图①﹣2
若△APC的面积等于△ABC面积的一半;则PD=BC,即点P为BA中点,
此时,点P移动的距离为AC+CB+BP=12+9+=cm,
移动的时间为:÷3=秒,
答案:或;
(2)△APQ≌△DEF,即,对应顶点为A与D,P与E,Q与F;
①当点P在AC上,如图②﹣1所示:
此时,AP=4,AQ=5,
∴点Q移动的速度为5÷(4÷3)=cm/s,
②当点P在AB上,如图②﹣2所示:
此时,AP=4,AQ=5,
即,点P移动的距离为9+12+15﹣4=32cm,点Q移动的距离为9+12+15﹣5=31cm,
∴点Q移动的速度为31÷(32÷3)=cm/s,
综上所述,两点运动过程中的某一时刻,恰好△APQ≌△DEF,
点Q的运动速为cm/s或cm/s.
(?http:?/??/?www.21cnjy.com?)
(?http:?/??/?www.21cnjy.com?)
(?http:?/??/?www.21cnjy.com?)
(?http:?/??/?www.21cnjy.com?)
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
