【人教版八上高频易错必刷题】12.2 三角形全等的判定(含解析)
文档属性
| 名称 | 【人教版八上高频易错必刷题】12.2 三角形全等的判定(含解析) | 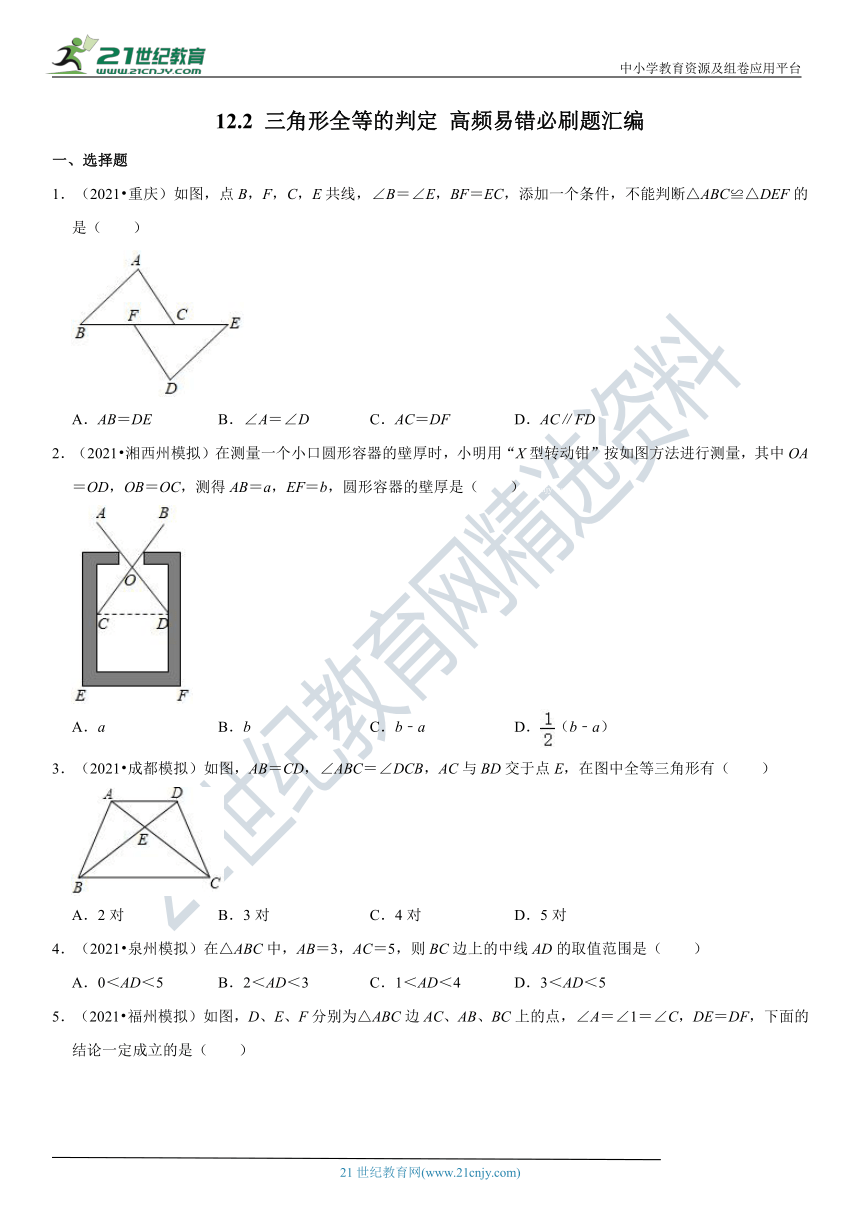 | |
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-18 18:23:44 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
12.2
三角形全等的判定
高频易错必刷题汇编
一、选择题
1.(2021?重庆)如图,点B,F,C,E共线,∠B=∠E,BF=EC,添加一个条件,不能判断△ABC≌△DEF的是( )www.21-cn-jy.com
(?http:?/??/?www.21cnjy.com?)
A.AB=DE
B.∠A=∠D
C.AC=DF
D.AC∥FD
2.(2021?湘西州模拟)在测量一个小口圆
(?http:?/??/?www.21cnjy.com?)形容器的壁厚时,小明用“X型转动钳”按如图方法进行测量,其中OA=OD,OB=OC,测得AB=a,EF=b,圆形容器的壁厚是( )21
cnjy
com
(?http:?/??/?www.21cnjy.com?)
A.a
B.b
C.b﹣a
D.(b﹣a)
3.(2021?成都模拟)如图,AB=CD,∠ABC=∠DCB,AC与BD交于点E,在图中全等三角形有( )
(?http:?/??/?www.21cnjy.com?)
A.2对
B.3对
C.4对
D.5对
4.(2021?泉州模拟)在△ABC中,AB=3,AC=5,则BC边上的中线AD的取值范围是( )
A.0<AD<5
B.2<AD<3
C.1<AD<4
D.3<AD<5
5.(2021?福州模拟)如图,D、E
(?http:?/??/?www.21cnjy.com?)、F分别为△ABC边AC、AB、BC上的点,∠A=∠1=∠C,DE=DF,下面的结论一定成立的是( )
(?http:?/??/?www.21cnjy.com?)
A.AE=FC
B.AE=DE
C.AE+FC=AC
D.AD+FC=AB
6.(2021?衡水模拟)如图,已知点C是
(?http:?/??/?www.21cnjy.com?)∠AOB的平分线上一点,点P、P′分别在边OA、OB上.如果要得到OP=OP′,需要添加以下条件中的某一个即可,请你写出所有可能的结果的序号为( )
①∠OCP=∠OCP′;
②∠OPC=∠OP′C;
③PC=P′C;
④PP′⊥OC.
(?http:?/??/?www.21cnjy.com?)
A.①②
B.④③
C.①②④
D.①④③
7.(2021?唐山模拟)如图,有一张三角形
(?http:?/??/?www.21cnjy.com?)纸片ABC,已知∠B=∠C=x°,按下列方案用剪刀沿着箭头方向剪开,可能得不到全等三角形纸片的是( )
A.
(?http:?/??/?www.21cnjy.com?)
B.
(?http:?/??/?www.21cnjy.com?)
C.
(?http:?/??/?www.21cnjy.com?)
D.
(?http:?/??/?www.21cnjy.com?)
8.(2021?合肥模拟)如图,∠O=
(?http:?/??/?www.21cnjy.com?)60°,∠ACB的两边与∠O的两边分别交于点A,B,且∠ACB=120°,CA=CB,点P在射线OA上,OP=20,则CP的最小值是( )
(?http:?/??/?www.21cnjy.com?)
A.10
B.
C.
D.15
9.(2021?长沙模拟
(?http:?/??/?www.21cnjy.com?))如图,菱形ABCD中,E在边AB上,F在射线BC上,DE与AF交于点G,DE=AF,其中∠B=45°,∠AED=30°,AE=2,则EG的长度为( )
(?http:?/??/?www.21cnjy.com?)
A.
B.4
C.
D.
10.(2020?湖北)如图,已知△A
(?http:?/??/?www.21cnjy.com?)BC和△ADE都是等腰三角形,∠BAC=∠DAE=90°,BD,CE交于点F,连接AF.下列结论:①BD=CE;②BF⊥CF;③AF平分∠CAD;④∠AFE=45°.其中正确结论的个数有( )
(?http:?/??/?www.21cnjy.com?)
A.1个
B.2个
C.3个
D.4个
二、填空题
11.(2021?昆明模拟)
(?http:?/??/?www.21cnjy.com?)小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、3、4的四块),你认为将其中的
块带去,就能配一块大小和形状与原来都一样的三角形.
(?http:?/??/?www.21cnjy.com?)
12.(2021?石家庄
(?http:?/??/?www.21cnjy.com?)模拟)如图,△ABC中,∠ABC=2∠C,AP和BQ分别为∠BAC和∠ABC的角平分线,若△ABQ的周长为20,BP=4,则AB的长为
.
(?http:?/??/?www.21cnjy.com?)
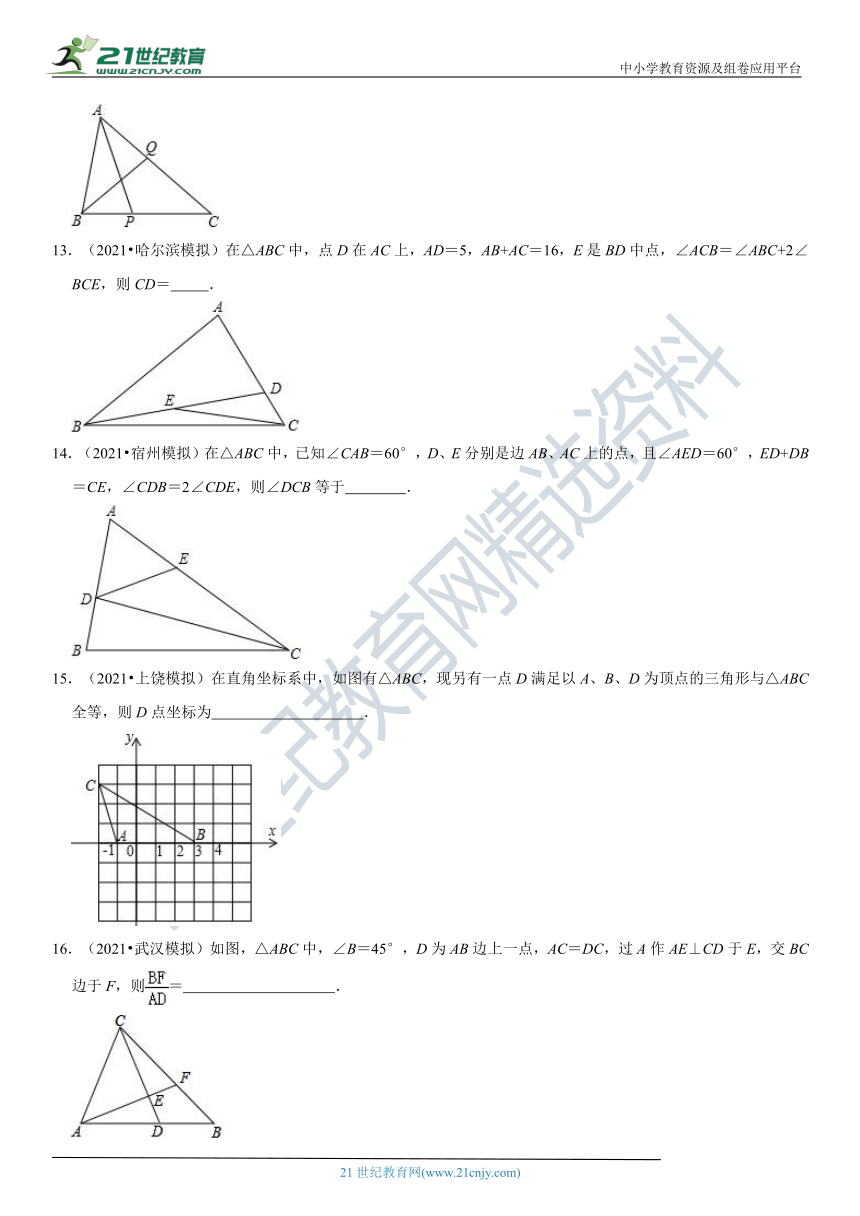
13.(2021?哈尔滨
(?http:?/??/?www.21cnjy.com?)模拟)在△ABC中,点D在AC上,AD=5,AB+AC=16,E是BD中点,∠ACB=∠ABC+2∠BCE,则CD=
.
(?http:?/??/?www.21cnjy.com?)
14.(2021?宿州模拟)在△ABC中,已
(?http:?/??/?www.21cnjy.com?)知∠CAB=60°,D、E分别是边AB、AC上的点,且∠AED=60°,ED+DB=CE,∠CDB=2∠CDE,则∠DCB等于
.【出处:21教育名师】
(?http:?/??/?www.21cnjy.com?)
15.(2021?上饶模拟)在直角坐标
(?http:?/??/?www.21cnjy.com?)系中,如图有△ABC,现另有一点D满足以A、B、D为顶点的三角形与△ABC全等,则D点坐标为
.
(?http:?/??/?www.21cnjy.com?)
16.(2021?武汉模拟)如图,△ABC中,∠B=45°,D为AB边上一点,AC=DC,过A作AE⊥CD于E,交BC边于F,则=
.
(?http:?/??/?www.21cnjy.com?)
三、解答题
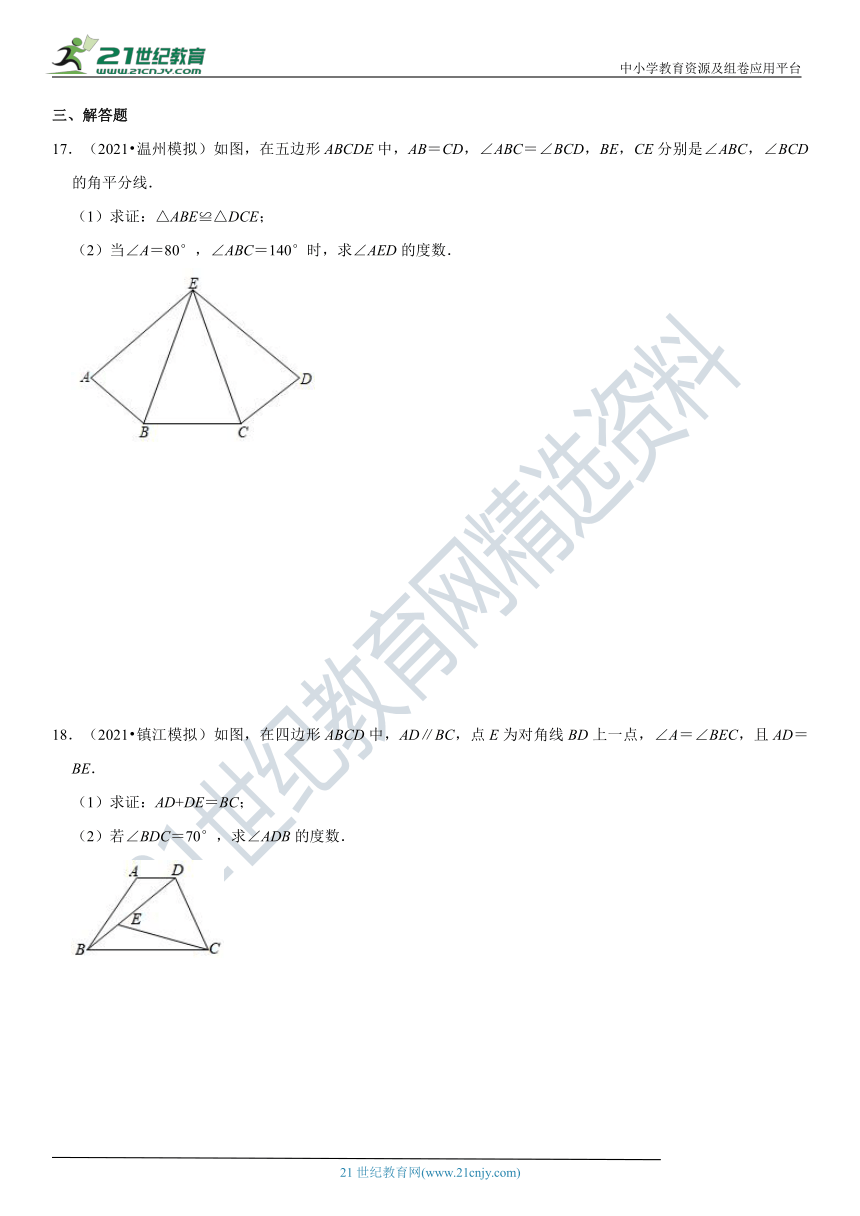
17.(2021?温州模拟)如图,在五边形ABCDE中,AB=CD,∠ABC=∠BCD,BE,CE分别是∠ABC,∠BCD的角平分线.【来源:21·世纪·教育·网】
(1)求证:△ABE≌△DCE;
(2)当∠A=80°,∠ABC=140°时,求∠AED的度数.
(?http:?/??/?www.21cnjy.com?)
18.(2021?镇江模拟)如图,在四边形ABCD中,AD∥BC,点E为对角线BD上一点,∠A=∠BEC,且AD=BE.
(1)求证:AD+DE=BC;
(2)若∠BDC=70°,求∠ADB的度数.
(?http:?/??/?www.21cnjy.com?)
19.(2021?北京模拟)如图,四边形AB
(?http:?/??/?www.21cnjy.com?)CD中,AB∥CD,CD=AD,∠ADC=60°,对角线BD平分∠ABC交AC于点P.CE是∠ACB的角平分线,交BD于点O.21教育名师原创作品
(1)请求出∠BAC的度数;
(2)试用等式表示线段BE、BC、CP之间的数量关系,并说明理由.
(?http:?/??/?www.21cnjy.com?)
20.(2021?杭州)在①AD=AE,②∠ABE=∠ACD,③FB=FC这三个条件中选择其中一个,补充在下面的问题中,并完成问题的解答.21cnjy.com
问题:如图,在△ABC中,
(?http:?/??/?www.21cnjy.com?)∠ABC=∠ACB,点D在AB边上(不与点A,点B重合),点E在AC边上(不与点A,点C重合),连接BE,CD,BE与CD相交于点F.若
,求证:BE=CD.
注:如果选择多个条件分别作答,按第一个解答计分.
(?http:?/??/?www.21cnjy.com?)
12.2
三角形全等的判定
高频易错必刷题汇编
一、选择题
1.(2021?重庆)如图,点B,F,C,E共线,∠B=∠E,BF=EC,添加一个条件,不能判断△ABC≌△DEF的是( )
(?http:?/??/?www.21cnjy.com?)
A.AB=DE
B.∠A=∠D
C.AC=DF
D.AC∥FD
解:∵BF=EC,
∴BF+FC=EC+FC,
∴BC=EF,
又∵∠B=∠E,
∴当添加条件AB=DE时,△ABC≌△DEF(SAS),故选项A不符合题意;
当添加条件∠A=∠D时,△ABC≌△DEF(AAS),故选项B不符合题意;
当添加条件AC=DF时,无法判断△ABC≌△DEF,故选项C符合题意;
当添加条件AC∥FD时,则∠ACB=∠DFE,故△ABC≌△DEF(ASA),故选项D不符合题意;
答案:C.
2.(2021?湘西州模拟
(?http:?/??/?www.21cnjy.com?))在测量一个小口圆形容器的壁厚时,小明用“X型转动钳”按如图方法进行测量,其中OA=OD,OB=OC,测得AB=a,EF=b,圆形容器的壁厚是( )21·cn·jy·com
(?http:?/??/?www.21cnjy.com?)
A.a
B.b
C.b﹣a
D.(b﹣a)
解:连接AB.
在△AOB和△DOC中,
,
∴△AOB≌△DOC(SAS),
∴AB=CD=a,
∵EF=b,
∴圆柱形容器的壁厚是(b﹣a),
答案:D.
(?http:?/??/?www.21cnjy.com?)
3.(2021?成都模拟)如图,AB=CD,∠ABC=∠DCB,AC与BD交于点E,在图中全等三角形有( )
(?http:?/??/?www.21cnjy.com?)
A.2对
B.3对
C.4对
D.5对
解:①△ABC≌△DCB;
∵AB=CD,∠ABC=∠DCB,
∵BC=CB,
∴△ABC≌△DCB;
②△ABE≌△DCE,
∵△ABC≌△DCB,
∴∠BAC=∠CDB,
∵AB=CD,∠AEB=∠DEC,
∴△ABE≌△CDE;
③△ABD≌△DCA,
∵∠BAC=∠CDB,∠AEB=∠DEC,
∴∠ABD=∠DCA,
∵AB=CD,BD=AC,
∴△ABD≌△DCA;
答案:B.
(?http:?/??/?www.21cnjy.com?)
4.(2021?泉州模拟)在△ABC中,AB=3,AC=5,则BC边上的中线AD的取值范围是( )
A.0<AD<5
B.2<AD<3
C.1<AD<4
D.3<AD<5
解:如图,延长AD至E,使DE=AD,连接CE,
∵AD是BC边上的中线,
∴BD=CD,
∠ADB=∠CDE,
∴△ABD≌△ECD,
∴CE=AB,
在△ACE中,AC﹣CE<AE<AC+CE,
而AB=3,AC=5,
∴5﹣3<AE<5+3,
∴2<2AD<8,
即1<AD<4.
答案:C.
(?http:?/??/?www.21cnjy.com?)
5.(2021?福州模拟)如图,D、E、F分
(?http:?/??/?www.21cnjy.com?)别为△ABC边AC、AB、BC上的点,∠A=∠1=∠C,DE=DF,下面的结论一定成立的是( )21·世纪
教育网
(?http:?/??/?www.21cnjy.com?)
A.AE=FC
B.AE=DE
C.AE+FC=AC
D.AD+FC=AB
解:∵∠A=∠1,∠CDE=∠1+∠CDF=∠A+∠AED,
∴∠CDF=∠AED,
在△ADE和△CFD中,,
∴△ADE≌△CFD(AAS),
∴AE=CD,AD=CF,
∴AE+FC=CD+AD=AC,
答案:C.
6.(2021?衡水模拟)如图,已知点C是
(?http:?/??/?www.21cnjy.com?)∠AOB的平分线上一点,点P、P′分别在边OA、OB上.如果要得到OP=OP′,需要添加以下条件中的某一个即可,请你写出所有可能的结果的序号为( )
①∠OCP=∠OCP′;
②∠OPC=∠OP′C;
③PC=P′C;
④PP′⊥OC.
(?http:?/??/?www.21cnjy.com?)
A.①②
B.④③
C.①②④
D.①④③
解:①若加∠OCP=∠OCP′,则根据ASA可证明△OPC≌△OP′C,得OP=OP′;
②若加∠OPC=∠OP′C,则根据AAS可证明△OPC≌△OP′C,得OP=OP′;
③若加PC=P′C,则不能证明△OPC≌△OP′C,不能得到OP=OP′;
④若加PP′⊥OC,则根据ASA可证明△OPD≌△OP′D,得OP=OP′.
答案:C.
(?http:?/??/?www.21cnjy.com?)
7.(2021?唐山模拟)如图,有一张三角
(?http:?/??/?www.21cnjy.com?)形纸片ABC,已知∠B=∠C=x°,按下列方案用剪刀沿着箭头方向剪开,可能得不到全等三角形纸片的是( )2·1·c·n·j·y
A.
(?http:?/??/?www.21cnjy.com?)
B.
(?http:?/??/?www.21cnjy.com?)
C.
(?http:?/??/?www.21cnjy.com?)
D.
(?http:?/??/?www.21cnjy.com?)
解:A、由全等三角形的判定定理SAS证得图中两个小三角形全等,
故本选项不符合题意;
B、由全等三角形的判定定理SAS证得图中两个小三角形全等,
故本选项不符合题意;
C、如图1,∵∠DEC=∠B+∠BDE,
∴x°+∠FEC=x°+∠BDE,
∴∠FEC=∠BDE,
所以其对应边应该是BE和CF,而已知给的是BD=FC=3,
所以不能判定两个小三角形全等,故本选项符合题意;
D、如图2,∵∠DEC=∠B+∠BDE,
∴x°+∠FEC=x°+∠BDE,
∴∠FEC=∠BDE,
∵BD=EC=2,∠B=∠C,
∴△BDE≌△CEF,
所以能判定两个小三角形全等,故本选项不符合题意;
由于本题选择可能得不到全等三角形纸片的图形,
答案:C.
(?http:?/??/?www.21cnjy.com?)
(?http:?/??/?www.21cnjy.com?)
8.(2021?合肥模拟)如图,∠O=60
(?http:?/??/?www.21cnjy.com?)°,∠ACB的两边与∠O的两边分别交于点A,B,且∠ACB=120°,CA=CB,点P在射线OA上,OP=20,则CP的最小值是( )21教育网
(?http:?/??/?www.21cnjy.com?)
A.10
B.
C.
D.15
解:如图,过点C作CM⊥OA,CN⊥OB,M,N为垂足,
(?http:?/??/?www.21cnjy.com?)
在四边形CMON中,∠MCN=360°﹣60°﹣90°﹣90°=120°,
∵∠ACM=∠BCA﹣∠BCM=120°﹣∠BCM,∠BCN=∠MCN﹣∠BCM=120°﹣∠BCM,
∴∠ACM=∠BCN,
在Rt△CAM与Rt△CBN中,
,
∴△CAM≌△CBN(AAS),
∴CM=CN,
根据到角的两边距离相等的点在角平分线上,可得,点C一定在∠AOB的平分线上,
过点P作PC'⊥OC交OC于点C',
在Rt△OPC'中,OP=20,∠POC'=30°,
则PC'=PO=10,
即CP的最小值为10,
答案:A.
9.(2021?长沙模拟)如图,菱形
(?http:?/??/?www.21cnjy.com?)ABCD中,E在边AB上,F在射线BC上,DE与AF交于点G,DE=AF,其中∠B=45°,∠AED=30°,AE=2,则EG的长度为( )【版权所有:21教育】
(?http:?/??/?www.21cnjy.com?)
A.
B.4
C.
D.
解:如图,作AN⊥BF于N,AH⊥DE于H,DM⊥BA交BA的延长线于M.
(?http:?/??/?www.21cnjy.com?)
∵四边形ABCD是菱形,
∴AB=AD,AD∥BC,
∴∠MAD=∠B=45°,
∵∠ANB=∠M=90°,
∴△ANB≌△AMD(AAS),
∴AN=DM,
∵∠M=∠ANF=90°,DE=AF.DM=AN,
∴Rt△ANF≌Rt△DME(HL),
∴∠MED=∠F=30°,
∴MAF=∠B+∠F=75°,
∵∠MAF=∠AEG+∠AGE,
∴∠AGE=45°,
在Rt△AEH中,∵AE=2,∠AEH=30°,
∴AH=AE=1,EH=AH=,
在Rt△AHG中,∵∠AGH=45°,
∴AH=GH=1,
∴EG=+1,
答案:D.
10.(2020?湖北)如图,已知△
(?http:?/??/?www.21cnjy.com?)ABC和△ADE都是等腰三角形,∠BAC=∠DAE=90°,BD,CE交于点F,连接AF.下列结论:①BD=CE;②BF⊥CF;③AF平分∠CAD;④∠AFE=45°.其中正确结论的个数有( )
(?http:?/??/?www.21cnjy.com?)
A.1个
B.2个
C.3个
D.4个
解:如图,作AM⊥BD于M,AN⊥EC于N,设AD交EF于O.
(?http:?/??/?www.21cnjy.com?)
∵∠BAC=∠DAE=90°,
∴∠BAD=∠CAE,
∵AB=AC,AD=AE,
∴△BAD≌△CAE(SAS),
∴EC=BD,∠BDA=∠AEC,故①正确
∵∠DOF=∠AOE,
∴∠DFO=∠EAO=90°,
∴BD⊥EC,故②正确,
∵△BAD≌△CAE,AM⊥BD,AN⊥EC,
∴AM=AN,
∴FA平分∠EFB,
∴∠AFE=45°,故④正确,
若③成立,则∠EAF=∠BAF,
∵∠AFE=∠AFB,
∴∠AEF=∠ABD=∠ADB,推出AB=AD,由题意知,AB不一定等于AD,
所以AF不一定平分∠CAD,故③错误,
答案:C.
二、填空题
11.(2021?昆明模拟
(?http:?/??/?www.21cnjy.com?))小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、3、4的四块),你认为将其中的 2 块带去,就能配一块大小和形状与原来都一样的三角形.
(?http:?/??/?www.21cnjy.com?)
解:1、3、4块玻璃不同时具备包括一完整边在内的三个证明全等的要素,所以不能带它们去,
只有第2块有完整的两角及夹边,符合ASA,满足题目要求的条件,是符合题意的.
答案:2.
12.(2021?石家庄模拟)如图,△
(?http:?/??/?www.21cnjy.com?)ABC中,∠ABC=2∠C,AP和BQ分别为∠BAC和∠ABC的角平分线,若△ABQ的周长为20,BP=4,则AB的长为 8 .
(?http:?/??/?www.21cnjy.com?)
解:∵BQ平分∠ABC,
∴∠CBQ=∠ABC,
∵∠ABC=2∠C,
∴∠CBQ=∠C,
∴BQ=CQ,
∴BQ+AQ=CQ+AQ=AC…①,
过点P作PD∥BQ交CQ于点D,如图所示:
则∠CPD=∠CBQ,∠ADP=∠AQB,
∵∠AQB=∠C+∠CBQ=2∠C,
∴∠ADP=2∠C,
∴∠ABC=∠ADP,
∵AP平分∠BAC,
∴∠BAP=∠CAP,
在△ABP与△ADP中,,
∴△ABP≌△ADP(AAS),
∴AB=AD,BP=PD,
∴AB+BP=AD+PD=AD+CD=AC…②,
由①②可得,BQ+AQ=AB+BP;
∵△ABQ的周长为20,BP=4,
∴AB+BQ+AQ=AB+BP+AB=20,
∴AB=8;
答案:8.
(?http:?/??/?www.21cnjy.com?)
13.(2021?哈尔滨模拟)在△ABC中
(?http:?/??/?www.21cnjy.com?),点D在AC上,AD=5,AB+AC=16,E是BD中点,∠ACB=∠ABC+2∠BCE,则CD= 2 .
(?http:?/??/?www.21cnjy.com?)
解:延长CE于F,使CE=EF,交AB于点G,
(?http:?/??/?www.21cnjy.com?)
∵E是BD的中点,
∴BE=DE,
在△BEF与△DEC中,
,
∴△BEF≌△DEC(SAS),
∴∠F=∠DCE,BF=DC,
∵∠ACB=∠ABC+2∠BCE,
∴∠DCE=∠ACB﹣∠BCE=∠ABC+∠BCE,
∵∠AGC=∠ABC+∠BCE,
∴∠AGC=∠DCE,
∴∠F=∠DCE=∠AGC=∠BGF,AG=AC,
∴BF=BG=CD,
设BF=BG=CD=x,
∵AD=5,AB+AC=16,
∴,
解得:x=2,
∴CD=2,
答案:2.
14.(2021?宿州模拟)在△ABC中,
(?http:?/??/?www.21cnjy.com?)已知∠CAB=60°,D、E分别是边AB、AC上的点,且∠AED=60°,ED+DB=CE,∠CDB=2∠CDE,则∠DCB等于 20° .
(?http:?/??/?www.21cnjy.com?)
解:延长AB到F使BF=AD,连接CF,如图,
∵∠CAD=60°,∠AED=60°,
∴△ADE为等边三角形,
∴AD=DE=AE,∠ADE=60°,
∴∠BDE=180°﹣∠ADE=120°,
∵∠CDB=2∠CDE,
∴3∠CDE=120°,解得∠CDE=40°,
∴∠CDB=2∠CDE=80°,
∵BF=AD,
∴BF=DE,
∵DE+BD=CE,
∴BF+BD=CE,即DF=CE,
∵AF=AD+DF,AC=AE+CE,
∴AF=AC,
而∠BAC=60°,
∴△AFC为等边三角形,
∴CF=AC,∠F=60°,
在△ACD和△FCB
中
,
∴△ACD≌△FCB
(SAS),
∴CB=CD,
∴∠CBD=∠CDB=80°,
∴∠DCB=180﹣(∠CBD+∠CDB)=20°.
(?http:?/??/?www.21cnjy.com?)
15.(2021?上饶模拟)在直角坐标
(?http:?/??/?www.21cnjy.com?)系中,如图有△ABC,现另有一点D满足以A、B、D为顶点的三角形与△ABC全等,则D点坐标为 (﹣2,﹣3)、(4,3)、(4,﹣3) .2-1-c-n-j-y
(?http:?/??/?www.21cnjy.com?)
解:点D的可能位置如下图所示:
(?http:?/??/?www.21cnjy.com?),
则可得点D的坐标为:(﹣2,﹣3)、(4,3)、(4,﹣3).
答案:(﹣2,﹣3)、(4,3)、(4,﹣3).
16.(2021?武汉模拟)如图,△ABC中,∠B=45°,D为AB边上一点,AC=DC,过A作AE⊥CD于E,交BC边于F,则= .
(?http:?/??/?www.21cnjy.com?)
解:过点C作CG⊥AD于点G,过点F作FH⊥AB于点H,
(?http:?/??/?www.21cnjy.com?)
∵AC=CD,
∴AG=GD,∠ACG=∠DCG,
∵∠AED=90°,
∴∠GAE=∠DCG,
∵∠B=45°,
∴FH=BH,∠GCB=45°,
∵∠AFC=45°+∠FAB,∠ACF=45°+∠ACG,
∴∠ACF=∠AFC,
∴AF=AC,
∴CD=AF,
∵∠CGD=∠AHF=90°,
∴△AFH≌△CDG(AAS),
∴GD=FH,
∵,AD=2GD,
∴.
答案:.
三、解答题
17.(2021?温州模拟)如图,在五边形ABCDE中,AB=CD,∠ABC=∠BCD,BE,CE分别是∠ABC,∠BCD的角平分线.
(1)求证:△ABE≌△DCE;
(2)当∠A=80°,∠ABC=140°时,求∠AED的度数.
(?http:?/??/?www.21cnjy.com?)
(1)证明:∵BE,CE分别是∠ABC,∠BCD的角平分线.
∴∠ABE=∠CBE,∠BCE=∠DCE,
∵∠ABC=∠BCD,
∴∠ABE=∠DCE,∠EBC=∠ECB,
∴BE=CE,
在△ABE和△DCE中,
,
∴△ABE≌△DCE(SAS);
(2)解:∵△ABE≌△DCE,
∴∠A=∠D=80°,
∵∠ABC=140°,
∴∠ABC=∠BCD=140°,
∵五边形ABCDE的内角和是540°,
∴∠AED=540°﹣∠A﹣∠D﹣∠ABC﹣∠BCD=540°﹣80°﹣80°﹣140°﹣140°=100°.
18.(2021?镇江模拟)如图,在四边形ABCD中,AD∥BC,点E为对角线BD上一点,∠A=∠BEC,且AD=BE.21世纪教育网版权所有
(1)求证:AD+DE=BC;
(2)若∠BDC=70°,求∠ADB的度数.
(?http:?/??/?www.21cnjy.com?)
证明:(1)∵AD∥BC,
∴∠ADB=∠CBE,
在△ADB和△EBC中,
,
∴△ADB≌△EBC(ASA),
∴BC=BD,
∵BE+DE=DB,
∴AD+DE=BC;
(2)∵BC=BD,
∴∠BDC=∠BCD=70°,
∴∠DBC=40°,
∴∠ADB=40°.
19.(2021?北京模拟)如图,
(?http:?/??/?www.21cnjy.com?)四边形ABCD中,AB∥CD,CD=AD,∠ADC=60°,对角线BD平分∠ABC交AC于点P.CE是∠ACB的角平分线,交BD于点O.【来源:21cnj
y.co
m】
(1)请求出∠BAC的度数;
(2)试用等式表示线段BE、BC、CP之间的数量关系,并说明理由.
(?http:?/??/?www.21cnjy.com?)
(1)解:∵CD=AD,∠ADC=60°,
∴△ACD为等边三角形,
∴∠ACD=60°,
∵AB∥CD,
∴∠BAC=∠ACD=60°;
(2)证明:在BC上截取BF=BE,
(?http:?/??/?www.21cnjy.com?)
∵BD平分∠ABC,
∴∠EBO=∠OBF,
∵OB=OB,
∴△BEO≌△BFO(SAS),
∴∠BOE=∠BOF,
∵∠BAC=60°,CE是∠ACB的角平分线,
∴∠OBC+∠OCB=60°,
∴∠POC=∠BOE=60°,
∴∠COF=60°,
∴∠COF=∠POC,
又∵OC=OC,∠OCP=∠OCF,
∴△CPO≌△CFO(ASA),
∴CP=CF,
∴BC=BF+CF=BE+CP.
20.(2021?杭州)在①AD=AE,②∠ABE=∠ACD,③FB=FC这三个条件中选择其中一个,补充在下面的问题中,并完成问题的解答.www-2-1-cnjy-com
问题:如图,在△ABC中,∠ABC=∠A
(?http:?/??/?www.21cnjy.com?)CB,点D在AB边上(不与点A,点B重合),点E在AC边上(不与点A,点C重合),连接BE,CD,BE与CD相交于点F.若
①AD=AE(②∠ABE=∠ACD或③FB=FC) ,求证:BE=CD.21
cnjy
com
注:如果选择多个条件分别作答,按第一个解答计分.
(?http:?/??/?www.21cnjy.com?)
证明:选择条件①的证明为:
∵∠ABC=∠ACB,
∴AB=AC,
在△ABE和△ACD中,
,
∴△ABE≌△ACD(SAS),
∴BE=CD;
选择条件②的证明为:
∵∠ABC=∠ACB,
∴AB=AC,
在△ABE和△ACD中,
,
∴△ABE≌△ACD(ASA),
∴BE=CD;
选择条件③的证明为:
∵∠ABC=∠ACB,
∴AB=AC,
∵FB=FC,
∴∠FBC=∠FCB,
∴∠ABC﹣∠FBC=∠ACB﹣∠FCB,
即∠ABE=∠ACD,
在△ABE和△ACD中,
,
∴△ABE≌△ACD(ASA),
∴BE=CD.
所以,①AD=AE(②∠ABE=∠ACD或③FB=FC)
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
12.2
三角形全等的判定
高频易错必刷题汇编
一、选择题
1.(2021?重庆)如图,点B,F,C,E共线,∠B=∠E,BF=EC,添加一个条件,不能判断△ABC≌△DEF的是( )www.21-cn-jy.com
(?http:?/??/?www.21cnjy.com?)
A.AB=DE
B.∠A=∠D
C.AC=DF
D.AC∥FD
2.(2021?湘西州模拟)在测量一个小口圆
(?http:?/??/?www.21cnjy.com?)形容器的壁厚时,小明用“X型转动钳”按如图方法进行测量,其中OA=OD,OB=OC,测得AB=a,EF=b,圆形容器的壁厚是( )21
cnjy
com
(?http:?/??/?www.21cnjy.com?)
A.a
B.b
C.b﹣a
D.(b﹣a)
3.(2021?成都模拟)如图,AB=CD,∠ABC=∠DCB,AC与BD交于点E,在图中全等三角形有( )
(?http:?/??/?www.21cnjy.com?)
A.2对
B.3对
C.4对
D.5对
4.(2021?泉州模拟)在△ABC中,AB=3,AC=5,则BC边上的中线AD的取值范围是( )
A.0<AD<5
B.2<AD<3
C.1<AD<4
D.3<AD<5
5.(2021?福州模拟)如图,D、E
(?http:?/??/?www.21cnjy.com?)、F分别为△ABC边AC、AB、BC上的点,∠A=∠1=∠C,DE=DF,下面的结论一定成立的是( )
(?http:?/??/?www.21cnjy.com?)
A.AE=FC
B.AE=DE
C.AE+FC=AC
D.AD+FC=AB
6.(2021?衡水模拟)如图,已知点C是
(?http:?/??/?www.21cnjy.com?)∠AOB的平分线上一点,点P、P′分别在边OA、OB上.如果要得到OP=OP′,需要添加以下条件中的某一个即可,请你写出所有可能的结果的序号为( )
①∠OCP=∠OCP′;
②∠OPC=∠OP′C;
③PC=P′C;
④PP′⊥OC.
(?http:?/??/?www.21cnjy.com?)
A.①②
B.④③
C.①②④
D.①④③
7.(2021?唐山模拟)如图,有一张三角形
(?http:?/??/?www.21cnjy.com?)纸片ABC,已知∠B=∠C=x°,按下列方案用剪刀沿着箭头方向剪开,可能得不到全等三角形纸片的是( )
A.
(?http:?/??/?www.21cnjy.com?)
B.
(?http:?/??/?www.21cnjy.com?)
C.
(?http:?/??/?www.21cnjy.com?)
D.
(?http:?/??/?www.21cnjy.com?)
8.(2021?合肥模拟)如图,∠O=
(?http:?/??/?www.21cnjy.com?)60°,∠ACB的两边与∠O的两边分别交于点A,B,且∠ACB=120°,CA=CB,点P在射线OA上,OP=20,则CP的最小值是( )
(?http:?/??/?www.21cnjy.com?)
A.10
B.
C.
D.15
9.(2021?长沙模拟
(?http:?/??/?www.21cnjy.com?))如图,菱形ABCD中,E在边AB上,F在射线BC上,DE与AF交于点G,DE=AF,其中∠B=45°,∠AED=30°,AE=2,则EG的长度为( )
(?http:?/??/?www.21cnjy.com?)
A.
B.4
C.
D.
10.(2020?湖北)如图,已知△A
(?http:?/??/?www.21cnjy.com?)BC和△ADE都是等腰三角形,∠BAC=∠DAE=90°,BD,CE交于点F,连接AF.下列结论:①BD=CE;②BF⊥CF;③AF平分∠CAD;④∠AFE=45°.其中正确结论的个数有( )
(?http:?/??/?www.21cnjy.com?)
A.1个
B.2个
C.3个
D.4个
二、填空题
11.(2021?昆明模拟)
(?http:?/??/?www.21cnjy.com?)小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、3、4的四块),你认为将其中的
块带去,就能配一块大小和形状与原来都一样的三角形.
(?http:?/??/?www.21cnjy.com?)
12.(2021?石家庄
(?http:?/??/?www.21cnjy.com?)模拟)如图,△ABC中,∠ABC=2∠C,AP和BQ分别为∠BAC和∠ABC的角平分线,若△ABQ的周长为20,BP=4,则AB的长为
.
(?http:?/??/?www.21cnjy.com?)
13.(2021?哈尔滨
(?http:?/??/?www.21cnjy.com?)模拟)在△ABC中,点D在AC上,AD=5,AB+AC=16,E是BD中点,∠ACB=∠ABC+2∠BCE,则CD=
.
(?http:?/??/?www.21cnjy.com?)
14.(2021?宿州模拟)在△ABC中,已
(?http:?/??/?www.21cnjy.com?)知∠CAB=60°,D、E分别是边AB、AC上的点,且∠AED=60°,ED+DB=CE,∠CDB=2∠CDE,则∠DCB等于
.【出处:21教育名师】
(?http:?/??/?www.21cnjy.com?)
15.(2021?上饶模拟)在直角坐标
(?http:?/??/?www.21cnjy.com?)系中,如图有△ABC,现另有一点D满足以A、B、D为顶点的三角形与△ABC全等,则D点坐标为
.
(?http:?/??/?www.21cnjy.com?)
16.(2021?武汉模拟)如图,△ABC中,∠B=45°,D为AB边上一点,AC=DC,过A作AE⊥CD于E,交BC边于F,则=
.
(?http:?/??/?www.21cnjy.com?)
三、解答题
17.(2021?温州模拟)如图,在五边形ABCDE中,AB=CD,∠ABC=∠BCD,BE,CE分别是∠ABC,∠BCD的角平分线.【来源:21·世纪·教育·网】
(1)求证:△ABE≌△DCE;
(2)当∠A=80°,∠ABC=140°时,求∠AED的度数.
(?http:?/??/?www.21cnjy.com?)
18.(2021?镇江模拟)如图,在四边形ABCD中,AD∥BC,点E为对角线BD上一点,∠A=∠BEC,且AD=BE.
(1)求证:AD+DE=BC;
(2)若∠BDC=70°,求∠ADB的度数.
(?http:?/??/?www.21cnjy.com?)
19.(2021?北京模拟)如图,四边形AB
(?http:?/??/?www.21cnjy.com?)CD中,AB∥CD,CD=AD,∠ADC=60°,对角线BD平分∠ABC交AC于点P.CE是∠ACB的角平分线,交BD于点O.21教育名师原创作品
(1)请求出∠BAC的度数;
(2)试用等式表示线段BE、BC、CP之间的数量关系,并说明理由.
(?http:?/??/?www.21cnjy.com?)
20.(2021?杭州)在①AD=AE,②∠ABE=∠ACD,③FB=FC这三个条件中选择其中一个,补充在下面的问题中,并完成问题的解答.21cnjy.com
问题:如图,在△ABC中,
(?http:?/??/?www.21cnjy.com?)∠ABC=∠ACB,点D在AB边上(不与点A,点B重合),点E在AC边上(不与点A,点C重合),连接BE,CD,BE与CD相交于点F.若
,求证:BE=CD.
注:如果选择多个条件分别作答,按第一个解答计分.
(?http:?/??/?www.21cnjy.com?)
12.2
三角形全等的判定
高频易错必刷题汇编
一、选择题
1.(2021?重庆)如图,点B,F,C,E共线,∠B=∠E,BF=EC,添加一个条件,不能判断△ABC≌△DEF的是( )
(?http:?/??/?www.21cnjy.com?)
A.AB=DE
B.∠A=∠D
C.AC=DF
D.AC∥FD
解:∵BF=EC,
∴BF+FC=EC+FC,
∴BC=EF,
又∵∠B=∠E,
∴当添加条件AB=DE时,△ABC≌△DEF(SAS),故选项A不符合题意;
当添加条件∠A=∠D时,△ABC≌△DEF(AAS),故选项B不符合题意;
当添加条件AC=DF时,无法判断△ABC≌△DEF,故选项C符合题意;
当添加条件AC∥FD时,则∠ACB=∠DFE,故△ABC≌△DEF(ASA),故选项D不符合题意;
答案:C.
2.(2021?湘西州模拟
(?http:?/??/?www.21cnjy.com?))在测量一个小口圆形容器的壁厚时,小明用“X型转动钳”按如图方法进行测量,其中OA=OD,OB=OC,测得AB=a,EF=b,圆形容器的壁厚是( )21·cn·jy·com
(?http:?/??/?www.21cnjy.com?)
A.a
B.b
C.b﹣a
D.(b﹣a)
解:连接AB.
在△AOB和△DOC中,
,
∴△AOB≌△DOC(SAS),
∴AB=CD=a,
∵EF=b,
∴圆柱形容器的壁厚是(b﹣a),
答案:D.
(?http:?/??/?www.21cnjy.com?)
3.(2021?成都模拟)如图,AB=CD,∠ABC=∠DCB,AC与BD交于点E,在图中全等三角形有( )
(?http:?/??/?www.21cnjy.com?)
A.2对
B.3对
C.4对
D.5对
解:①△ABC≌△DCB;
∵AB=CD,∠ABC=∠DCB,
∵BC=CB,
∴△ABC≌△DCB;
②△ABE≌△DCE,
∵△ABC≌△DCB,
∴∠BAC=∠CDB,
∵AB=CD,∠AEB=∠DEC,
∴△ABE≌△CDE;
③△ABD≌△DCA,
∵∠BAC=∠CDB,∠AEB=∠DEC,
∴∠ABD=∠DCA,
∵AB=CD,BD=AC,
∴△ABD≌△DCA;
答案:B.
(?http:?/??/?www.21cnjy.com?)
4.(2021?泉州模拟)在△ABC中,AB=3,AC=5,则BC边上的中线AD的取值范围是( )
A.0<AD<5
B.2<AD<3
C.1<AD<4
D.3<AD<5
解:如图,延长AD至E,使DE=AD,连接CE,
∵AD是BC边上的中线,
∴BD=CD,
∠ADB=∠CDE,
∴△ABD≌△ECD,
∴CE=AB,
在△ACE中,AC﹣CE<AE<AC+CE,
而AB=3,AC=5,
∴5﹣3<AE<5+3,
∴2<2AD<8,
即1<AD<4.
答案:C.
(?http:?/??/?www.21cnjy.com?)
5.(2021?福州模拟)如图,D、E、F分
(?http:?/??/?www.21cnjy.com?)别为△ABC边AC、AB、BC上的点,∠A=∠1=∠C,DE=DF,下面的结论一定成立的是( )21·世纪
教育网
(?http:?/??/?www.21cnjy.com?)
A.AE=FC
B.AE=DE
C.AE+FC=AC
D.AD+FC=AB
解:∵∠A=∠1,∠CDE=∠1+∠CDF=∠A+∠AED,
∴∠CDF=∠AED,
在△ADE和△CFD中,,
∴△ADE≌△CFD(AAS),
∴AE=CD,AD=CF,
∴AE+FC=CD+AD=AC,
答案:C.
6.(2021?衡水模拟)如图,已知点C是
(?http:?/??/?www.21cnjy.com?)∠AOB的平分线上一点,点P、P′分别在边OA、OB上.如果要得到OP=OP′,需要添加以下条件中的某一个即可,请你写出所有可能的结果的序号为( )
①∠OCP=∠OCP′;
②∠OPC=∠OP′C;
③PC=P′C;
④PP′⊥OC.
(?http:?/??/?www.21cnjy.com?)
A.①②
B.④③
C.①②④
D.①④③
解:①若加∠OCP=∠OCP′,则根据ASA可证明△OPC≌△OP′C,得OP=OP′;
②若加∠OPC=∠OP′C,则根据AAS可证明△OPC≌△OP′C,得OP=OP′;
③若加PC=P′C,则不能证明△OPC≌△OP′C,不能得到OP=OP′;
④若加PP′⊥OC,则根据ASA可证明△OPD≌△OP′D,得OP=OP′.
答案:C.
(?http:?/??/?www.21cnjy.com?)
7.(2021?唐山模拟)如图,有一张三角
(?http:?/??/?www.21cnjy.com?)形纸片ABC,已知∠B=∠C=x°,按下列方案用剪刀沿着箭头方向剪开,可能得不到全等三角形纸片的是( )2·1·c·n·j·y
A.
(?http:?/??/?www.21cnjy.com?)
B.
(?http:?/??/?www.21cnjy.com?)
C.
(?http:?/??/?www.21cnjy.com?)
D.
(?http:?/??/?www.21cnjy.com?)
解:A、由全等三角形的判定定理SAS证得图中两个小三角形全等,
故本选项不符合题意;
B、由全等三角形的判定定理SAS证得图中两个小三角形全等,
故本选项不符合题意;
C、如图1,∵∠DEC=∠B+∠BDE,
∴x°+∠FEC=x°+∠BDE,
∴∠FEC=∠BDE,
所以其对应边应该是BE和CF,而已知给的是BD=FC=3,
所以不能判定两个小三角形全等,故本选项符合题意;
D、如图2,∵∠DEC=∠B+∠BDE,
∴x°+∠FEC=x°+∠BDE,
∴∠FEC=∠BDE,
∵BD=EC=2,∠B=∠C,
∴△BDE≌△CEF,
所以能判定两个小三角形全等,故本选项不符合题意;
由于本题选择可能得不到全等三角形纸片的图形,
答案:C.
(?http:?/??/?www.21cnjy.com?)
(?http:?/??/?www.21cnjy.com?)
8.(2021?合肥模拟)如图,∠O=60
(?http:?/??/?www.21cnjy.com?)°,∠ACB的两边与∠O的两边分别交于点A,B,且∠ACB=120°,CA=CB,点P在射线OA上,OP=20,则CP的最小值是( )21教育网
(?http:?/??/?www.21cnjy.com?)
A.10
B.
C.
D.15
解:如图,过点C作CM⊥OA,CN⊥OB,M,N为垂足,
(?http:?/??/?www.21cnjy.com?)
在四边形CMON中,∠MCN=360°﹣60°﹣90°﹣90°=120°,
∵∠ACM=∠BCA﹣∠BCM=120°﹣∠BCM,∠BCN=∠MCN﹣∠BCM=120°﹣∠BCM,
∴∠ACM=∠BCN,
在Rt△CAM与Rt△CBN中,
,
∴△CAM≌△CBN(AAS),
∴CM=CN,
根据到角的两边距离相等的点在角平分线上,可得,点C一定在∠AOB的平分线上,
过点P作PC'⊥OC交OC于点C',
在Rt△OPC'中,OP=20,∠POC'=30°,
则PC'=PO=10,
即CP的最小值为10,
答案:A.
9.(2021?长沙模拟)如图,菱形
(?http:?/??/?www.21cnjy.com?)ABCD中,E在边AB上,F在射线BC上,DE与AF交于点G,DE=AF,其中∠B=45°,∠AED=30°,AE=2,则EG的长度为( )【版权所有:21教育】
(?http:?/??/?www.21cnjy.com?)
A.
B.4
C.
D.
解:如图,作AN⊥BF于N,AH⊥DE于H,DM⊥BA交BA的延长线于M.
(?http:?/??/?www.21cnjy.com?)
∵四边形ABCD是菱形,
∴AB=AD,AD∥BC,
∴∠MAD=∠B=45°,
∵∠ANB=∠M=90°,
∴△ANB≌△AMD(AAS),
∴AN=DM,
∵∠M=∠ANF=90°,DE=AF.DM=AN,
∴Rt△ANF≌Rt△DME(HL),
∴∠MED=∠F=30°,
∴MAF=∠B+∠F=75°,
∵∠MAF=∠AEG+∠AGE,
∴∠AGE=45°,
在Rt△AEH中,∵AE=2,∠AEH=30°,
∴AH=AE=1,EH=AH=,
在Rt△AHG中,∵∠AGH=45°,
∴AH=GH=1,
∴EG=+1,
答案:D.
10.(2020?湖北)如图,已知△
(?http:?/??/?www.21cnjy.com?)ABC和△ADE都是等腰三角形,∠BAC=∠DAE=90°,BD,CE交于点F,连接AF.下列结论:①BD=CE;②BF⊥CF;③AF平分∠CAD;④∠AFE=45°.其中正确结论的个数有( )
(?http:?/??/?www.21cnjy.com?)
A.1个
B.2个
C.3个
D.4个
解:如图,作AM⊥BD于M,AN⊥EC于N,设AD交EF于O.
(?http:?/??/?www.21cnjy.com?)
∵∠BAC=∠DAE=90°,
∴∠BAD=∠CAE,
∵AB=AC,AD=AE,
∴△BAD≌△CAE(SAS),
∴EC=BD,∠BDA=∠AEC,故①正确
∵∠DOF=∠AOE,
∴∠DFO=∠EAO=90°,
∴BD⊥EC,故②正确,
∵△BAD≌△CAE,AM⊥BD,AN⊥EC,
∴AM=AN,
∴FA平分∠EFB,
∴∠AFE=45°,故④正确,
若③成立,则∠EAF=∠BAF,
∵∠AFE=∠AFB,
∴∠AEF=∠ABD=∠ADB,推出AB=AD,由题意知,AB不一定等于AD,
所以AF不一定平分∠CAD,故③错误,
答案:C.
二、填空题
11.(2021?昆明模拟
(?http:?/??/?www.21cnjy.com?))小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、3、4的四块),你认为将其中的 2 块带去,就能配一块大小和形状与原来都一样的三角形.
(?http:?/??/?www.21cnjy.com?)
解:1、3、4块玻璃不同时具备包括一完整边在内的三个证明全等的要素,所以不能带它们去,
只有第2块有完整的两角及夹边,符合ASA,满足题目要求的条件,是符合题意的.
答案:2.
12.(2021?石家庄模拟)如图,△
(?http:?/??/?www.21cnjy.com?)ABC中,∠ABC=2∠C,AP和BQ分别为∠BAC和∠ABC的角平分线,若△ABQ的周长为20,BP=4,则AB的长为 8 .
(?http:?/??/?www.21cnjy.com?)
解:∵BQ平分∠ABC,
∴∠CBQ=∠ABC,
∵∠ABC=2∠C,
∴∠CBQ=∠C,
∴BQ=CQ,
∴BQ+AQ=CQ+AQ=AC…①,
过点P作PD∥BQ交CQ于点D,如图所示:
则∠CPD=∠CBQ,∠ADP=∠AQB,
∵∠AQB=∠C+∠CBQ=2∠C,
∴∠ADP=2∠C,
∴∠ABC=∠ADP,
∵AP平分∠BAC,
∴∠BAP=∠CAP,
在△ABP与△ADP中,,
∴△ABP≌△ADP(AAS),
∴AB=AD,BP=PD,
∴AB+BP=AD+PD=AD+CD=AC…②,
由①②可得,BQ+AQ=AB+BP;
∵△ABQ的周长为20,BP=4,
∴AB+BQ+AQ=AB+BP+AB=20,
∴AB=8;
答案:8.
(?http:?/??/?www.21cnjy.com?)
13.(2021?哈尔滨模拟)在△ABC中
(?http:?/??/?www.21cnjy.com?),点D在AC上,AD=5,AB+AC=16,E是BD中点,∠ACB=∠ABC+2∠BCE,则CD= 2 .
(?http:?/??/?www.21cnjy.com?)
解:延长CE于F,使CE=EF,交AB于点G,
(?http:?/??/?www.21cnjy.com?)
∵E是BD的中点,
∴BE=DE,
在△BEF与△DEC中,
,
∴△BEF≌△DEC(SAS),
∴∠F=∠DCE,BF=DC,
∵∠ACB=∠ABC+2∠BCE,
∴∠DCE=∠ACB﹣∠BCE=∠ABC+∠BCE,
∵∠AGC=∠ABC+∠BCE,
∴∠AGC=∠DCE,
∴∠F=∠DCE=∠AGC=∠BGF,AG=AC,
∴BF=BG=CD,
设BF=BG=CD=x,
∵AD=5,AB+AC=16,
∴,
解得:x=2,
∴CD=2,
答案:2.
14.(2021?宿州模拟)在△ABC中,
(?http:?/??/?www.21cnjy.com?)已知∠CAB=60°,D、E分别是边AB、AC上的点,且∠AED=60°,ED+DB=CE,∠CDB=2∠CDE,则∠DCB等于 20° .
(?http:?/??/?www.21cnjy.com?)
解:延长AB到F使BF=AD,连接CF,如图,
∵∠CAD=60°,∠AED=60°,
∴△ADE为等边三角形,
∴AD=DE=AE,∠ADE=60°,
∴∠BDE=180°﹣∠ADE=120°,
∵∠CDB=2∠CDE,
∴3∠CDE=120°,解得∠CDE=40°,
∴∠CDB=2∠CDE=80°,
∵BF=AD,
∴BF=DE,
∵DE+BD=CE,
∴BF+BD=CE,即DF=CE,
∵AF=AD+DF,AC=AE+CE,
∴AF=AC,
而∠BAC=60°,
∴△AFC为等边三角形,
∴CF=AC,∠F=60°,
在△ACD和△FCB
中
,
∴△ACD≌△FCB
(SAS),
∴CB=CD,
∴∠CBD=∠CDB=80°,
∴∠DCB=180﹣(∠CBD+∠CDB)=20°.
(?http:?/??/?www.21cnjy.com?)
15.(2021?上饶模拟)在直角坐标
(?http:?/??/?www.21cnjy.com?)系中,如图有△ABC,现另有一点D满足以A、B、D为顶点的三角形与△ABC全等,则D点坐标为 (﹣2,﹣3)、(4,3)、(4,﹣3) .2-1-c-n-j-y
(?http:?/??/?www.21cnjy.com?)
解:点D的可能位置如下图所示:
(?http:?/??/?www.21cnjy.com?),
则可得点D的坐标为:(﹣2,﹣3)、(4,3)、(4,﹣3).
答案:(﹣2,﹣3)、(4,3)、(4,﹣3).
16.(2021?武汉模拟)如图,△ABC中,∠B=45°,D为AB边上一点,AC=DC,过A作AE⊥CD于E,交BC边于F,则= .
(?http:?/??/?www.21cnjy.com?)
解:过点C作CG⊥AD于点G,过点F作FH⊥AB于点H,
(?http:?/??/?www.21cnjy.com?)
∵AC=CD,
∴AG=GD,∠ACG=∠DCG,
∵∠AED=90°,
∴∠GAE=∠DCG,
∵∠B=45°,
∴FH=BH,∠GCB=45°,
∵∠AFC=45°+∠FAB,∠ACF=45°+∠ACG,
∴∠ACF=∠AFC,
∴AF=AC,
∴CD=AF,
∵∠CGD=∠AHF=90°,
∴△AFH≌△CDG(AAS),
∴GD=FH,
∵,AD=2GD,
∴.
答案:.
三、解答题
17.(2021?温州模拟)如图,在五边形ABCDE中,AB=CD,∠ABC=∠BCD,BE,CE分别是∠ABC,∠BCD的角平分线.
(1)求证:△ABE≌△DCE;
(2)当∠A=80°,∠ABC=140°时,求∠AED的度数.
(?http:?/??/?www.21cnjy.com?)
(1)证明:∵BE,CE分别是∠ABC,∠BCD的角平分线.
∴∠ABE=∠CBE,∠BCE=∠DCE,
∵∠ABC=∠BCD,
∴∠ABE=∠DCE,∠EBC=∠ECB,
∴BE=CE,
在△ABE和△DCE中,
,
∴△ABE≌△DCE(SAS);
(2)解:∵△ABE≌△DCE,
∴∠A=∠D=80°,
∵∠ABC=140°,
∴∠ABC=∠BCD=140°,
∵五边形ABCDE的内角和是540°,
∴∠AED=540°﹣∠A﹣∠D﹣∠ABC﹣∠BCD=540°﹣80°﹣80°﹣140°﹣140°=100°.
18.(2021?镇江模拟)如图,在四边形ABCD中,AD∥BC,点E为对角线BD上一点,∠A=∠BEC,且AD=BE.21世纪教育网版权所有
(1)求证:AD+DE=BC;
(2)若∠BDC=70°,求∠ADB的度数.
(?http:?/??/?www.21cnjy.com?)
证明:(1)∵AD∥BC,
∴∠ADB=∠CBE,
在△ADB和△EBC中,
,
∴△ADB≌△EBC(ASA),
∴BC=BD,
∵BE+DE=DB,
∴AD+DE=BC;
(2)∵BC=BD,
∴∠BDC=∠BCD=70°,
∴∠DBC=40°,
∴∠ADB=40°.
19.(2021?北京模拟)如图,
(?http:?/??/?www.21cnjy.com?)四边形ABCD中,AB∥CD,CD=AD,∠ADC=60°,对角线BD平分∠ABC交AC于点P.CE是∠ACB的角平分线,交BD于点O.【来源:21cnj
y.co
m】
(1)请求出∠BAC的度数;
(2)试用等式表示线段BE、BC、CP之间的数量关系,并说明理由.
(?http:?/??/?www.21cnjy.com?)
(1)解:∵CD=AD,∠ADC=60°,
∴△ACD为等边三角形,
∴∠ACD=60°,
∵AB∥CD,
∴∠BAC=∠ACD=60°;
(2)证明:在BC上截取BF=BE,
(?http:?/??/?www.21cnjy.com?)
∵BD平分∠ABC,
∴∠EBO=∠OBF,
∵OB=OB,
∴△BEO≌△BFO(SAS),
∴∠BOE=∠BOF,
∵∠BAC=60°,CE是∠ACB的角平分线,
∴∠OBC+∠OCB=60°,
∴∠POC=∠BOE=60°,
∴∠COF=60°,
∴∠COF=∠POC,
又∵OC=OC,∠OCP=∠OCF,
∴△CPO≌△CFO(ASA),
∴CP=CF,
∴BC=BF+CF=BE+CP.
20.(2021?杭州)在①AD=AE,②∠ABE=∠ACD,③FB=FC这三个条件中选择其中一个,补充在下面的问题中,并完成问题的解答.www-2-1-cnjy-com
问题:如图,在△ABC中,∠ABC=∠A
(?http:?/??/?www.21cnjy.com?)CB,点D在AB边上(不与点A,点B重合),点E在AC边上(不与点A,点C重合),连接BE,CD,BE与CD相交于点F.若
①AD=AE(②∠ABE=∠ACD或③FB=FC) ,求证:BE=CD.21
cnjy
com
注:如果选择多个条件分别作答,按第一个解答计分.
(?http:?/??/?www.21cnjy.com?)
证明:选择条件①的证明为:
∵∠ABC=∠ACB,
∴AB=AC,
在△ABE和△ACD中,
,
∴△ABE≌△ACD(SAS),
∴BE=CD;
选择条件②的证明为:
∵∠ABC=∠ACB,
∴AB=AC,
在△ABE和△ACD中,
,
∴△ABE≌△ACD(ASA),
∴BE=CD;
选择条件③的证明为:
∵∠ABC=∠ACB,
∴AB=AC,
∵FB=FC,
∴∠FBC=∠FCB,
∴∠ABC﹣∠FBC=∠ACB﹣∠FCB,
即∠ABE=∠ACD,
在△ABE和△ACD中,
,
∴△ABE≌△ACD(ASA),
∴BE=CD.
所以,①AD=AE(②∠ABE=∠ACD或③FB=FC)
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
