【人教版八上高频易错必刷题】12.3 角的平分线的性质(含解析)
文档属性
| 名称 | 【人教版八上高频易错必刷题】12.3 角的平分线的性质(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-18 18:23:56 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
12.3
角的平分线的性质
高频易错必刷题汇编
一、选择题
1.(2020?牡丹江)
(?http:?/??/?www.21cnjy.com?)如图,直线l1、l2、l3表示三条相互交叉的公路,现要建一个货物中转站,要求它的三条公路的距离相等,则可供选择的地址有( )21教育网
(?http:?/??/?www.21cnjy.com?)
A.一处
B.二处
C.三处
D.四处
2.(2021?青海)如图,在四边形ABCD中,∠A=90°,AD=3,BC=5,对角线BD平分∠ABC,则△BCD的面积为( )21cnjy.com
(?http:?/??/?www.21cnjy.com?)
A.8
B.7.5
C.15
D.无法确定
3.(2021?贵阳模拟
(?http:?/??/?www.21cnjy.com?))如图,在△ABC中,∠C=90°,BC=1,AC=2,BD是∠ABC的平分线,设△ABD,△BCD的面积分别是S1,S2,则S1:S2等于( )
(?http:?/??/?www.21cnjy.com?)
A.2:1
B.:1
C.3:2
D.2:
4.(2021?茂名模拟)如图,已知点O为
(?http:?/??/?www.21cnjy.com?)△ABC的两条角平分线的交点,过点O作OD⊥BC,垂足为D,且OD=4.若△ABC的面积是34,则△ABC的周长为( )
(?http:?/??/?www.21cnjy.com?)
A.8.5
B.15
C.17
D.34
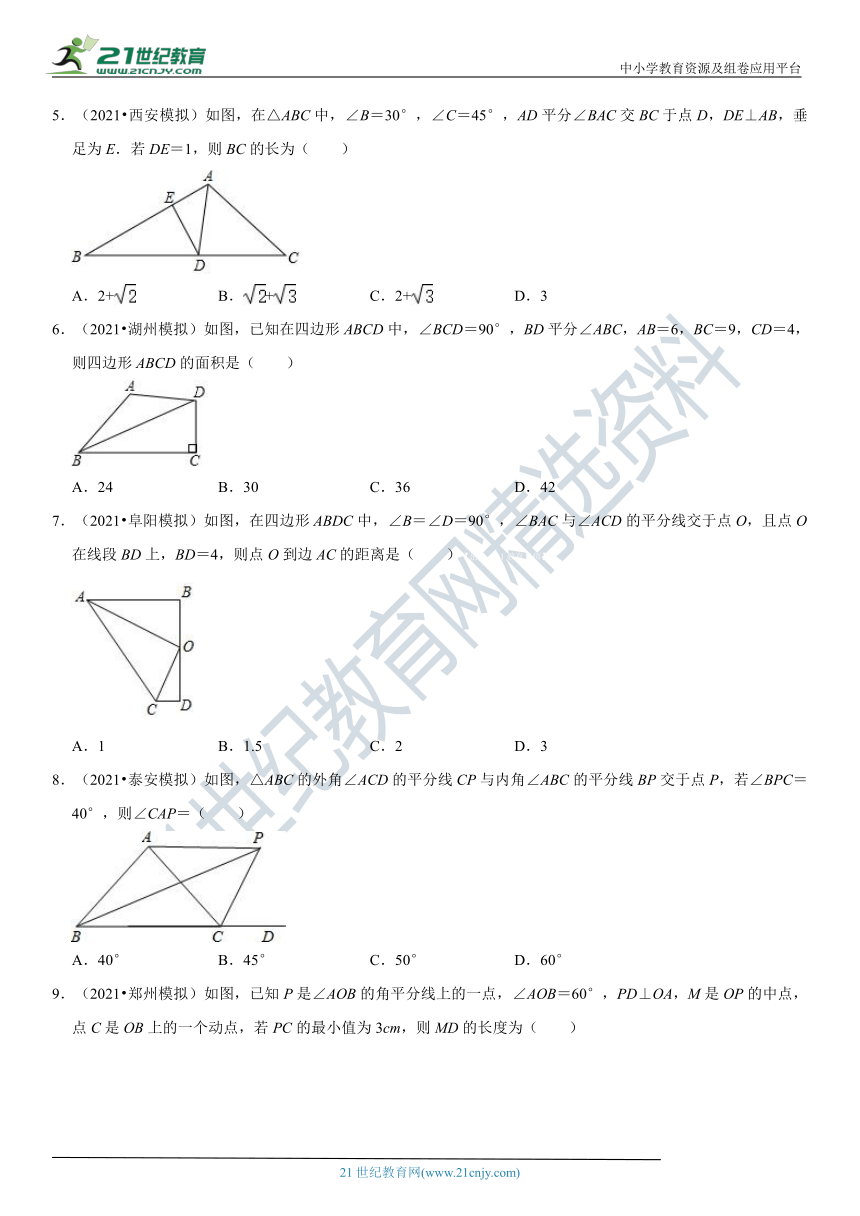
5.(2021?西安模拟)如图,在△ABC
(?http:?/??/?www.21cnjy.com?)中,∠B=30°,∠C=45°,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E.若DE=1,则BC的长为( )21·cn·jy·com
(?http:?/??/?www.21cnjy.com?)
A.2+
B.+
C.2+
D.3
6.(2021?湖州模拟)如图,
(?http:?/??/?www.21cnjy.com?)已知在四边形ABCD中,∠BCD=90°,BD平分∠ABC,AB=6,BC=9,CD=4,则四边形ABCD的面积是( )
(?http:?/??/?www.21cnjy.com?)
A.24
B.30
C.36
D.42
7.(2021?阜阳模拟)如图,在四边形A
(?http:?/??/?www.21cnjy.com?)BDC中,∠B=∠D=90°,∠BAC与∠ACD的平分线交于点O,且点O在线段BD上,BD=4,则点O到边AC的距离是( )【出处:21教育名师】
(?http:?/??/?www.21cnjy.com?)
A.1
B.1.5
C.2
D.3
8.(2021?泰安模拟)如图,△ABC
(?http:?/??/?www.21cnjy.com?)的外角∠ACD的平分线CP与内角∠ABC的平分线BP交于点P,若∠BPC=40°,则∠CAP=( )
(?http:?/??/?www.21cnjy.com?)
A.40°
B.45°
C.50°
D.60°
9.(2021?郑州模拟)如图,已知P
(?http:?/??/?www.21cnjy.com?)是∠AOB的角平分线上的一点,∠AOB=60°,PD⊥OA,M是OP的中点,点C是OB上的一个动点,若PC的最小值为3cm,则MD的长度为( )
(?http:?/??/?www.21cnjy.com?)
A.3cm
B.3cm
C.2cm
D.2cm
10.(2021?西安模拟)如图,在△AB
(?http:?/??/?www.21cnjy.com?)C中,∠BAC=90°,AD是BC边上的高,BE是AC边的中线,CF是∠ACB的角平分线,CF交AD于点G,交BE于点H,下面说法正确的是( )
①△ABE的面积=△BCE的面积;②∠FAG=∠FCB;③AF=AG;④BH=CH.
(?http:?/??/?www.21cnjy.com?)
A.①②③④
B.①②③
C.②④
D.①③
二、填空题
11.(2021?襄阳模拟)如
(?http:?/??/?www.21cnjy.com?)图,已知△ABC的周长是32,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=6,△ABC的面积是
.2·1·c·n·j·y
(?http:?/??/?www.21cnjy.com?)
12.(2021?合肥模拟)如图
(?http:?/??/?www.21cnjy.com?),四边形ABCD中,AB⊥AD,点E是BC边的中点,DA平分对角线BD与CD边延长线的夹角,若BD=5,CD=7,则AE=
.
(?http:?/??/?www.21cnjy.com?)
13.(2021?株洲模拟)在△ABC中,若
(?http:?/??/?www.21cnjy.com?)其内部的点P满足∠APB=∠BPC=∠CPA=120°,则称P为△ABC的费马点.如图所示,在△ABC中,已知∠BAC=45°,设P为△ABC的费马点,且满足∠PBA=45°,PA=4,则△PAC的面积为
.
(?http:?/??/?www.21cnjy.com?)
14.(2021?衡水模拟)如图,
(?http:?/??/?www.21cnjy.com?)△ABC中,BD平分∠ABC,交AC于D,DE⊥AB于点E,△ABC的面积是42cm2,AB=10cm,BC=14cm,则DE=
cm.
(?http:?/??/?www.21cnjy.com?)
15.(2020?牡丹江)已知如图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC,∠CED=35°,则∠EAB是
度.
(?http:?/??/?www.21cnjy.com?)
16.(2021?贵阳模拟)如图,在△BCD
(?http:?/??/?www.21cnjy.com?)中,∠BDC=90°,以BD为斜边,向外作Rt△ABD.若AD=4,∠ADB=∠C.且P是BC边上一动点,则DP长的最小值为
.
(?http:?/??/?www.21cnjy.com?)
三、解答题
17.(2021?上海模拟)如图,△ABC中
(?http:?/??/?www.21cnjy.com?),∠B的平分线BD与∠C的外角平分线CE交于点P.求证:点P到三边AB、BC、CA所在的直线的距离相等.
(?http:?/??/?www.21cnjy.com?)
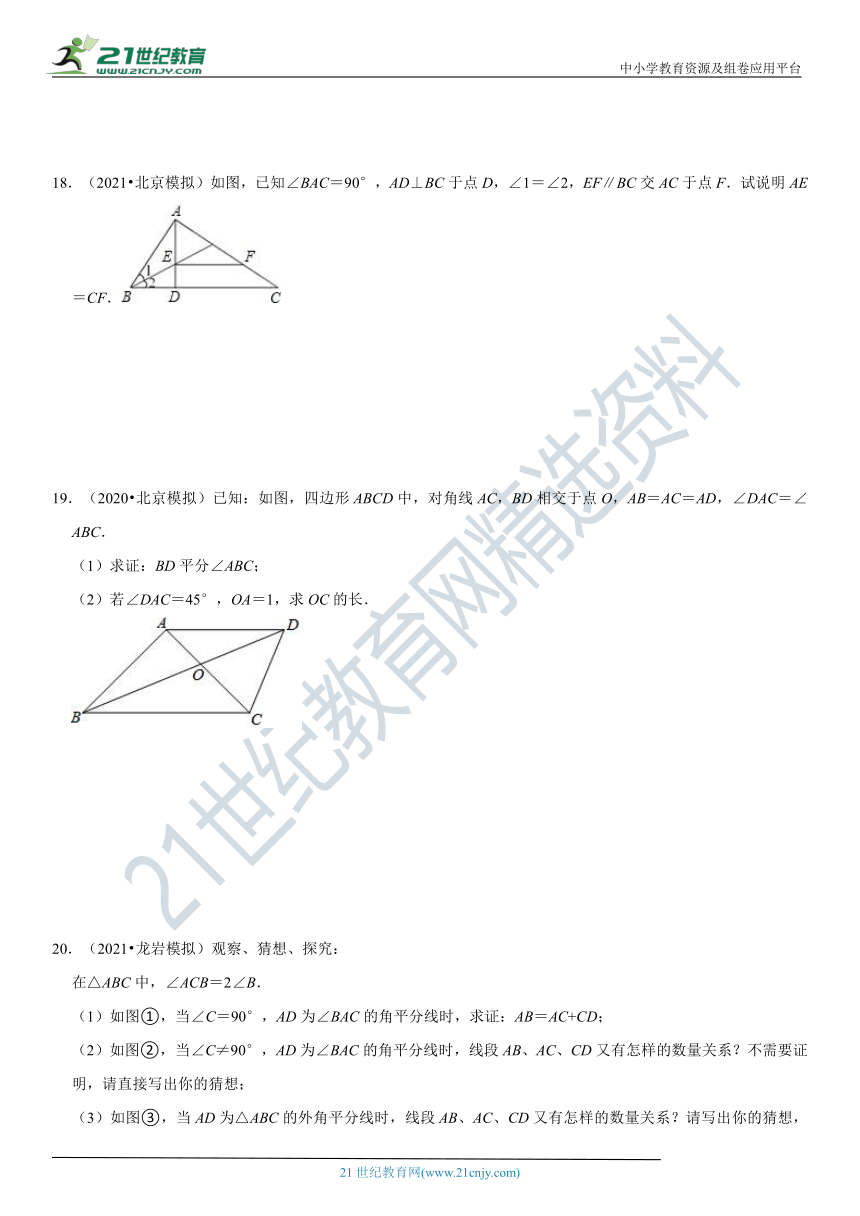
18.(2021?北京模拟)如图,已知∠BAC=90°,AD⊥BC于点D,∠1=∠2,EF∥BC交AC于点F.试说明AE=CF.
(?http:?/??/?www.21cnjy.com?)
19.(2020?北京模拟)已知:如图,四边形ABCD中,对角线AC,BD相交于点O,AB=AC=AD,∠DAC=∠ABC.
(1)求证:BD平分∠ABC;
(2)若∠DAC=45°,OA=1,求OC的长.
(?http:?/??/?www.21cnjy.com?)
20.(2021?龙岩模拟)观察、猜想、探究:
在△ABC中,∠ACB=2∠B.
(1)如图①,当∠C=90°,AD为∠BAC的角平分线时,求证:AB=AC+CD;
(2)如图②,当∠C≠90°,AD为∠BAC的角平分线时,线段AB、AC、CD又有怎样的数量关系?不需要证明,请直接写出你的猜想;www-2-1-cnjy-com
(3)如图③,当AD为△ABC的外角平分线时,线段AB、AC、CD又有怎样的数量关系?请写出你的猜想,并对你的猜想给予证明.
(?http:?/??/?www.21cnjy.com?)
12.3
角的平分线的性质
高频易错必刷题汇编
一、选择题
1.(2020?牡丹江)如图,直线l1、
(?http:?/??/?www.21cnjy.com?)l2、l3表示三条相互交叉的公路,现要建一个货物中转站,要求它的三条公路的距离相等,则可供选择的地址有( )www.21-cn-jy.com
(?http:?/??/?www.21cnjy.com?)
A.一处
B.二处
C.三处
D.四处
解:作直线l1、l2、l3所围成的三角形的外
(?http:?/??/?www.21cnjy.com?)角平分线和内角平分线,外角平分线相交于点P1、P2、P3,内角平分线相交于点P4,根据角平分线的性质可得到这4个点到三条公路的距离分别相等.
答案:D.
(?http:?/??/?www.21cnjy.com?)
2.(2021?青海)如图,在四边形ABCD中,∠A=90°,AD=3,BC=5,对角线BD平分∠ABC,则△BCD的面积为( )
(?http:?/??/?www.21cnjy.com?)
A.8
B.7.5
C.15
D.无法确定
解:过D点作DE⊥BC于E,如图,
∵BD平分∠ABC,DE⊥BC,DA⊥AB,
∴DE=DA=3,
∴△BCD的面积=×5×3=7.5.
答案:B.
(?http:?/??/?www.21cnjy.com?)
3.(2021?贵阳模拟)如图,在△ABC
(?http:?/??/?www.21cnjy.com?)中,∠C=90°,BC=1,AC=2,BD是∠ABC的平分线,设△ABD,△BCD的面积分别是S1,S2,则S1:S2等于( )
(?http:?/??/?www.21cnjy.com?)
A.2:1
B.:1
C.3:2
D.2:
解:过D作DE⊥AB于E,则DE=DC
(?http:?/??/?www.21cnjy.com?)
又∠C=90°,BC=1,AC=2,
∴AB==,
∴S1:S2=AB:BC=:1.
答案:B.
4.(2021?茂名模拟)
(?http:?/??/?www.21cnjy.com?)如图,已知点O为△ABC的两条角平分线的交点,过点O作OD⊥BC,垂足为D,且OD=4.若△ABC的面积是34,则△ABC的周长为( )
(?http:?/??/?www.21cnjy.com?)
A.8.5
B.15
C.17
D.34
解:∵点O为△ABC的两条角平分线的交点,
∴点O到△ABC各边的距离相等,
而OD⊥BC,OD=4,
∴点O到△ABC各边的距离为4,
∵S△ABC=S△AOB+S△BOC+S△AOC,
∴×AB×4+×AC×4+×BC×4=34,
∴AB+AC+BC=17,
即△ABC的周长为17.
答案:C.
5.(2021?西安模拟)如图,在△ABC中
(?http:?/??/?www.21cnjy.com?),∠B=30°,∠C=45°,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E.若DE=1,则BC的长为( )
(?http:?/??/?www.21cnjy.com?)
A.2+
B.+
C.2+
D.3
解:过点D作DF⊥AC于F,如图所示,
∵AD为∠BAC的平分线,且DE⊥AB于E,DF⊥AC于F,
∴DE=DF=1,
在Rt△BED中,∠B=30°,
∴BD=2DE=2,
在Rt△CDF中,∠C=45°,
∴△CDF为等腰直角三角形,
∴CD=DF=,
∴BC=BD+CD=2,
答案:A.
(?http:?/??/?www.21cnjy.com?)
6.(2021?湖州模拟)如图,已知
(?http:?/??/?www.21cnjy.com?)在四边形ABCD中,∠BCD=90°,BD平分∠ABC,AB=6,BC=9,CD=4,则四边形ABCD的面积是( )21·世纪
教育网
(?http:?/??/?www.21cnjy.com?)
A.24
B.30
C.36
D.42
解:过D作DH⊥AB交BA的延长线于H,
∵BD平分∠ABC,∠BCD=90°,
∴DH=CD=4,
∴四边形ABCD的面积=S△ABD+S△BCD=AB?DH+BC?CD=×6×4+×9×4=30,
答案:B.
(?http:?/??/?www.21cnjy.com?)
7.(2021?阜阳模拟)如图,在四边形AB
(?http:?/??/?www.21cnjy.com?)DC中,∠B=∠D=90°,∠BAC与∠ACD的平分线交于点O,且点O在线段BD上,BD=4,则点O到边AC的距离是( )【来源:21·世纪·教育·网】
(?http:?/??/?www.21cnjy.com?)
A.1
B.1.5
C.2
D.3
解:过O作OE⊥AC于E,
∵∠B=∠D=90°,∠BAC与∠ACD的平分线交于点O,
∴OB=OE=OD,
∵BD=4,
∴OB=OE=OD=2,
∴点O到边AC的距离是2,
答案:C.
(?http:?/??/?www.21cnjy.com?)
8.(2021?泰安模拟)如图,△ABC的外
(?http:?/??/?www.21cnjy.com?)角∠ACD的平分线CP与内角∠ABC的平分线BP交于点P,若∠BPC=40°,则∠CAP=( )21
cnjy
com
(?http:?/??/?www.21cnjy.com?)
A.40°
B.45°
C.50°
D.60°
解:延长BA,作PN⊥BD,PF⊥BA,PM⊥AC,
设∠PCD=x°,
∵CP平分∠ACD,
∴∠ACP=∠PCD=x°,PM=PN,
∵BP平分∠ABC,
∴∠ABP=∠PBC,PF=PN,
∴PF=PM,
∵∠BPC=40°,
∴∠ABP=∠PBC=∠PCD﹣∠BPC=(x﹣40)°,
∴∠BAC=∠ACD﹣∠ABC=2x°﹣(x°﹣40°)﹣(x°﹣40°)=80°,
∴∠CAF=100°,
在Rt△PFA和Rt△PMA中,
,
∴Rt△PFA≌Rt△PMA(HL),
∴∠FAP=∠PAC=50°.
答案:C.
(?http:?/??/?www.21cnjy.com?)
9.(2021?郑州模拟)如图,已知P是∠
(?http:?/??/?www.21cnjy.com?)AOB的角平分线上的一点,∠AOB=60°,PD⊥OA,M是OP的中点,点C是OB上的一个动点,若PC的最小值为3cm,则MD的长度为( )
(?http:?/??/?www.21cnjy.com?)
A.3cm
B.3cm
C.2cm
D.2cm
解:作PC⊥OB于C,则此时PC最小,
∵P是∠AOB的角平分线上的一点,PD⊥OA,PC⊥OB,
∴PD=PC=3,∠AOP=30°,
∴OP=2PD=6,
∵PD⊥OA,M是OP的中点,
∴DM=OP=3,
答案:A.
(?http:?/??/?www.21cnjy.com?)
10.(2021?西安模拟)如图
(?http:?/??/?www.21cnjy.com?),在△ABC中,∠BAC=90°,AD是BC边上的高,BE是AC边的中线,CF是∠ACB的角平分线,CF交AD于点G,交BE于点H,下面说法正确的是( )
①△ABE的面积=△BCE的面积;②∠FAG=∠FCB;③AF=AG;④BH=CH.
(?http:?/??/?www.21cnjy.com?)
A.①②③④
B.①②③
C.②④
D.①③
解:∵BE是AC边的中线,
∴AE=CE,
∵△ABE的面积=,△BCE的面积=AB,
∴△ABE的面积=△BCE的面积,故①正确;
∵AD是BC边上的高,
∴∠ADC=90°,
∵∠BAC=90°,
∴∠DAC+∠ACB=90°,∠FAG+∠DAC=90°,
∴∠FAG=∠ACB,
∵CF是∠ACB的角平分线,
∴∠ACF=∠FCB,∠ACB=2∠FCB,
∴∠FAG=2∠FCB,故②错误;
∵在△ACF和△DGC中,∠BAC=∠ADC=90°,∠ACF=∠FCB,
∴∠AFG=180°﹣∠BAC﹣∠ACF,∠AGF=∠DGC=180°﹣∠ADC﹣∠FCB,
∴∠AFG=∠AGF,
∴AF=AG,故③正确;
根据已知不能推出∠HBC=∠HCB,即不能推出HB=HC,故④错误;
即正确的为①③,
答案:D.
(?http:?/??/?www.21cnjy.com?)
二、填空题
11.(2021?襄阳模拟)如图
(?http:?/??/?www.21cnjy.com?),已知△ABC的周长是32,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=6,△ABC的面积是 96 .
(?http:?/??/?www.21cnjy.com?)
解:过O作OM⊥AB,ON⊥AC,连接AO,
∵OB,OC分别平分∠ABC和∠ACB,
∴OM=ON=OD=6,
∴△ABC的面积为:×AB×OM+BC×DO+NO=(AB+BC+AC)×DO=32×6=96.
答案:96.
(?http:?/??/?www.21cnjy.com?)
12.(2021?合肥模拟)如图,
(?http:?/??/?www.21cnjy.com?)四边形ABCD中,AB⊥AD,点E是BC边的中点,DA平分对角线BD与CD边延长线的夹角,若BD=5,CD=7,则AE= 6 .
(?http:?/??/?www.21cnjy.com?)
解:如图,
(?http:?/??/?www.21cnjy.com?)
取BD中点H,连AH、EH,
∵AB⊥AD,
∴AH=DH=BH=BD=2.5,
∴∠HDA=∠HAD,
∵DA平分∠FDB,
∴∠FDA=∠HDA,
∴∠FDA=∠HAD,
∴AH∥DF,
∵点E是BC边的中点,点H是BD的中点,
∴EH∥CD,EH=CD=3.5,
∴A、H、E三点共线,
∴AE=AH+EH=2.5+3.5=6.
13.(2021?株洲模拟)在△ABC中,若其内部的点P满足∠APB=∠BPC=∠CPA=120°,则称P为△ABC的费马点.如图所示,在△ABC中,已知∠BAC=45°,设P为△ABC的费马点,且满足∠PBA=45°,PA=4,则△PAC的面积为 4 .2-1-c-n-j-y
(?http:?/??/?www.21cnjy.com?)
解:如图,延长BP交AC于D,
(?http:?/??/?www.21cnjy.com?)
∵∠BAC=∠PBA=45°,
∴∠ADB=90°,AD=BD,
∵P为△ABC的费马点,
∴∠APB=∠CPA=120°,
∴∠BAP=180°﹣120°﹣45°=15°,
∴∠PAC=45°﹣15°=30°,
∴∠APD=60°,
Rt△PAD中,∵PA=4,
∴PD=2,AD=2,
∵∠APC=120°,
∴∠CPD=120°﹣60°=60°,
Rt△PDC中,∠PCD=30°,
∴CD=2,
∴AC=AD+CD=2+2=4,
∴△PAC的面积为==4.
答案:4.
14.(2021?衡水模拟)如图,△ABC中,BD平分∠ABC,交AC于D,DE⊥AB于点E,△ABC的面积是42cm2,AB=10cm,BC=14cm,则DE= cm.21教育名师原创作品
(?http:?/??/?www.21cnjy.com?)
解:作DF⊥BC于F,如图,
∵BD平分∠ABC,DE⊥AB,DF⊥BC,
∴DE=DF,
∵S△ADB+S△BCD=S△ABC,
∴×10×DE+×14×DF=42,
∴5DE+7DE=42,
∴DE=(cm).
答案:.
(?http:?/??/?www.21cnjy.com?)
15.(2020?牡丹江)已知如图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC,∠CED=35°,则∠EAB是 35 度.
(?http:?/??/?www.21cnjy.com?)
解:过点E作EF⊥AD,
∵DE平分∠ADC,且E是BC的中点,
∴CE=EB=EF,
又∵∠B=90°,且AE=AE,
∴△ABE≌△AFE,
∴∠EAB=∠EAF.
又∵∠CED=35°,∠C=90°,
∴∠CDE=90°﹣35°=55°,
∴∠CDA=110°,
∵∠B=∠C=90°,
∴DC∥AB,
∴∠CDA+∠DAB=180°,
∴∠DAB=70°,
∴∠EAB=35°.
答案:35.
(?http:?/??/?www.21cnjy.com?)
16.(2021?贵阳模拟)如图,在△B
(?http:?/??/?www.21cnjy.com?)CD中,∠BDC=90°,以BD为斜边,向外作Rt△ABD.若AD=4,∠ADB=∠C.且P是BC边上一动点,则DP长的最小值为 4 .21世纪教育网版权所有
(?http:?/??/?www.21cnjy.com?)
解:∵∠BDC=90°,∠A=90°,
∴∠ABD+∠ADB=90°,
∠C+∠CBD=90°,
∵∠ADB=∠C,
∴∠ABD=∠CBD,
由垂线段最短可知DP⊥BC时DP的长度最小,
此时,DP=AD,
∵AD=4,
∴DP的最小值为4.
答案:4.
(?http:?/??/?www.21cnjy.com?)
三、解答题
17.(2021?上海模拟)
(?http:?/??/?www.21cnjy.com?)如图,△ABC中,∠B的平分线BD与∠C的外角平分线CE交于点P.求证:点P到三边AB、BC、CA所在的直线的距离相等.【来源:21cnj
y.co
m】
(?http:?/??/?www.21cnjy.com?)
证明:如图,过点P作三边AB、BC、CA所在直线的垂线,垂足分别是Q、M、N.
则垂线段PQ、PM、PN,即为P点到三边AB、BC、CA所在直线的距离.
∵P是∠ABC的平分线BD上的一点,
∴PM=PQ.
∵P是∠ACM的平分线CE上的一点,
∴PM=PN.
∴PQ=PM=PN.
∴P点到三边AB、BC、CA所在直线的距离相等.
(?http:?/??/?www.21cnjy.com?)
18.(2021?北京模拟)如图,已知∠BAC=90°,AD⊥BC于点D,∠1=∠2,EF∥BC交AC于点F.试说明AE=CF.
(?http:?/??/?www.21cnjy.com?)【版权所有:21教育】
解:作EH⊥AB于H,作FG⊥BC于G,
∵∠1=∠2,AD⊥BC,
∴EH=ED(角平分线的性质)
∵EF∥BC,AD⊥BC,FG⊥BC,
∴四边形EFGD是矩形,
∴ED=FG,
∴EH=FG,
∵∠BAD+∠CAD=90°,∠C+∠CAD=90°,
∴∠BAD=∠C,
又∵∠AHE=∠FGC=90°,
∴△AEH≌△CFG(AAS)
∴AE=CF.
(?http:?/??/?www.21cnjy.com?)
19.(2020?北京模拟)已知:如图,四边形ABCD中,对角线AC,BD相交于点O,AB=AC=AD,∠DAC=∠ABC.21
cnjy
com
(1)求证:BD平分∠ABC;
(2)若∠DAC=45°,OA=1,求OC的长.
(?http:?/??/?www.21cnjy.com?)
(1)证明:∵AB=AC,
∴∠ABC=∠ACB,
∵∠DAC=∠ABC,
∴∠DAC=∠ACB.
∴AD∥BC,
∴∠ADB=∠CBD.
又∵AB=AD,
∴∠ADB=∠ABD.
∴∠ABD=∠CBD.
∴BD平分∠ABC;
(2)解:过点O作OE⊥BC于E,
∵∠DAC=45°,∠DAC=∠ABC,
∴∠ABC=∠ACB=45°,
∴∠B
AC=90°,
∵BD平分∠ABC,
∴OE=OA=1.
在Rt△OEC中,∠ACB=45°,OE=1,
∴OC=.
(?http:?/??/?www.21cnjy.com?)
20.(2021?龙岩模拟)观察、猜想、探究:
在△ABC中,∠ACB=2∠B.
(1)如图①,当∠C=90°,AD为∠BAC的角平分线时,求证:AB=AC+CD;
(2)如图②,当∠C≠90°,AD为∠BAC的角平分线时,线段AB、AC、CD又有怎样的数量关系?不需要证明,请直接写出你的猜想;
(3)如图③,当AD为△ABC的外角平分线时,线段AB、AC、CD又有怎样的数量关系?请写出你的猜想,并对你的猜想给予证明.
(?http:?/??/?www.21cnjy.com?)
(?http:?/??/?www.21cnjy.com?)
解:(1)过D作DE⊥AB,交AB于点E,如图1所示,
∵AD为∠BAC的平分线,DC⊥AC,DE⊥AB,
∴DE=DC,
在Rt△ACD和Rt△AED中,
AD=AD,DE=DC,
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE,∠ACB=∠AED,
∵∠ACB=2∠B,
∴∠AED=2∠B,
又∵∠AED=∠B+∠EDB,
∴∠B=∠EDB,
∴BE=DE=DC,
则AB=BE+AE=CD+AC;
(2)AB=CD+AC,理由为:
在AB上截取AG=AC,如图2所示,
∵AD为∠BAC的平分线,
∴∠GAD=∠CAD,
∵在△ADG和△ADC中,
,
∴△ADG≌△ADC(SAS),
∴CD=DG,∠AGD=∠ACB,
∵∠ACB=2∠B,
∴∠AGD=2∠B,
又∵∠AGD=∠B+∠GDB,
∴∠B=∠GDB,
∴BE=DG=DC,
则AB=BG+AG=CD+AC;
(3)AB=CD﹣AC,理由为:
在AF上截取AG=AC,如图3所示,
∵AD为∠FAC的平分线,
∴∠GAD=∠CAD,
∵在△ADG和△ACD中,
,
∴△ADG≌△ACD(SAS),
∴CD=GD,∠AGD=∠ACD,即∠ACB=∠FGD,
∵∠ACB=2∠B,
∴∠FGD=2∠B,
又∵∠FGD=∠B+∠GDB,
∴∠B=∠GDB,
∴BG=DG=DC,
则AB=BG﹣AG=CD﹣AC.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
12.3
角的平分线的性质
高频易错必刷题汇编
一、选择题
1.(2020?牡丹江)
(?http:?/??/?www.21cnjy.com?)如图,直线l1、l2、l3表示三条相互交叉的公路,现要建一个货物中转站,要求它的三条公路的距离相等,则可供选择的地址有( )21教育网
(?http:?/??/?www.21cnjy.com?)
A.一处
B.二处
C.三处
D.四处
2.(2021?青海)如图,在四边形ABCD中,∠A=90°,AD=3,BC=5,对角线BD平分∠ABC,则△BCD的面积为( )21cnjy.com
(?http:?/??/?www.21cnjy.com?)
A.8
B.7.5
C.15
D.无法确定
3.(2021?贵阳模拟
(?http:?/??/?www.21cnjy.com?))如图,在△ABC中,∠C=90°,BC=1,AC=2,BD是∠ABC的平分线,设△ABD,△BCD的面积分别是S1,S2,则S1:S2等于( )
(?http:?/??/?www.21cnjy.com?)
A.2:1
B.:1
C.3:2
D.2:
4.(2021?茂名模拟)如图,已知点O为
(?http:?/??/?www.21cnjy.com?)△ABC的两条角平分线的交点,过点O作OD⊥BC,垂足为D,且OD=4.若△ABC的面积是34,则△ABC的周长为( )
(?http:?/??/?www.21cnjy.com?)
A.8.5
B.15
C.17
D.34
5.(2021?西安模拟)如图,在△ABC
(?http:?/??/?www.21cnjy.com?)中,∠B=30°,∠C=45°,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E.若DE=1,则BC的长为( )21·cn·jy·com
(?http:?/??/?www.21cnjy.com?)
A.2+
B.+
C.2+
D.3
6.(2021?湖州模拟)如图,
(?http:?/??/?www.21cnjy.com?)已知在四边形ABCD中,∠BCD=90°,BD平分∠ABC,AB=6,BC=9,CD=4,则四边形ABCD的面积是( )
(?http:?/??/?www.21cnjy.com?)
A.24
B.30
C.36
D.42
7.(2021?阜阳模拟)如图,在四边形A
(?http:?/??/?www.21cnjy.com?)BDC中,∠B=∠D=90°,∠BAC与∠ACD的平分线交于点O,且点O在线段BD上,BD=4,则点O到边AC的距离是( )【出处:21教育名师】
(?http:?/??/?www.21cnjy.com?)
A.1
B.1.5
C.2
D.3
8.(2021?泰安模拟)如图,△ABC
(?http:?/??/?www.21cnjy.com?)的外角∠ACD的平分线CP与内角∠ABC的平分线BP交于点P,若∠BPC=40°,则∠CAP=( )
(?http:?/??/?www.21cnjy.com?)
A.40°
B.45°
C.50°
D.60°
9.(2021?郑州模拟)如图,已知P
(?http:?/??/?www.21cnjy.com?)是∠AOB的角平分线上的一点,∠AOB=60°,PD⊥OA,M是OP的中点,点C是OB上的一个动点,若PC的最小值为3cm,则MD的长度为( )
(?http:?/??/?www.21cnjy.com?)
A.3cm
B.3cm
C.2cm
D.2cm
10.(2021?西安模拟)如图,在△AB
(?http:?/??/?www.21cnjy.com?)C中,∠BAC=90°,AD是BC边上的高,BE是AC边的中线,CF是∠ACB的角平分线,CF交AD于点G,交BE于点H,下面说法正确的是( )
①△ABE的面积=△BCE的面积;②∠FAG=∠FCB;③AF=AG;④BH=CH.
(?http:?/??/?www.21cnjy.com?)
A.①②③④
B.①②③
C.②④
D.①③
二、填空题
11.(2021?襄阳模拟)如
(?http:?/??/?www.21cnjy.com?)图,已知△ABC的周长是32,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=6,△ABC的面积是
.2·1·c·n·j·y
(?http:?/??/?www.21cnjy.com?)
12.(2021?合肥模拟)如图
(?http:?/??/?www.21cnjy.com?),四边形ABCD中,AB⊥AD,点E是BC边的中点,DA平分对角线BD与CD边延长线的夹角,若BD=5,CD=7,则AE=
.
(?http:?/??/?www.21cnjy.com?)
13.(2021?株洲模拟)在△ABC中,若
(?http:?/??/?www.21cnjy.com?)其内部的点P满足∠APB=∠BPC=∠CPA=120°,则称P为△ABC的费马点.如图所示,在△ABC中,已知∠BAC=45°,设P为△ABC的费马点,且满足∠PBA=45°,PA=4,则△PAC的面积为
.
(?http:?/??/?www.21cnjy.com?)
14.(2021?衡水模拟)如图,
(?http:?/??/?www.21cnjy.com?)△ABC中,BD平分∠ABC,交AC于D,DE⊥AB于点E,△ABC的面积是42cm2,AB=10cm,BC=14cm,则DE=
cm.
(?http:?/??/?www.21cnjy.com?)
15.(2020?牡丹江)已知如图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC,∠CED=35°,则∠EAB是
度.
(?http:?/??/?www.21cnjy.com?)
16.(2021?贵阳模拟)如图,在△BCD
(?http:?/??/?www.21cnjy.com?)中,∠BDC=90°,以BD为斜边,向外作Rt△ABD.若AD=4,∠ADB=∠C.且P是BC边上一动点,则DP长的最小值为
.
(?http:?/??/?www.21cnjy.com?)
三、解答题
17.(2021?上海模拟)如图,△ABC中
(?http:?/??/?www.21cnjy.com?),∠B的平分线BD与∠C的外角平分线CE交于点P.求证:点P到三边AB、BC、CA所在的直线的距离相等.
(?http:?/??/?www.21cnjy.com?)
18.(2021?北京模拟)如图,已知∠BAC=90°,AD⊥BC于点D,∠1=∠2,EF∥BC交AC于点F.试说明AE=CF.
(?http:?/??/?www.21cnjy.com?)
19.(2020?北京模拟)已知:如图,四边形ABCD中,对角线AC,BD相交于点O,AB=AC=AD,∠DAC=∠ABC.
(1)求证:BD平分∠ABC;
(2)若∠DAC=45°,OA=1,求OC的长.
(?http:?/??/?www.21cnjy.com?)
20.(2021?龙岩模拟)观察、猜想、探究:
在△ABC中,∠ACB=2∠B.
(1)如图①,当∠C=90°,AD为∠BAC的角平分线时,求证:AB=AC+CD;
(2)如图②,当∠C≠90°,AD为∠BAC的角平分线时,线段AB、AC、CD又有怎样的数量关系?不需要证明,请直接写出你的猜想;www-2-1-cnjy-com
(3)如图③,当AD为△ABC的外角平分线时,线段AB、AC、CD又有怎样的数量关系?请写出你的猜想,并对你的猜想给予证明.
(?http:?/??/?www.21cnjy.com?)
12.3
角的平分线的性质
高频易错必刷题汇编
一、选择题
1.(2020?牡丹江)如图,直线l1、
(?http:?/??/?www.21cnjy.com?)l2、l3表示三条相互交叉的公路,现要建一个货物中转站,要求它的三条公路的距离相等,则可供选择的地址有( )www.21-cn-jy.com
(?http:?/??/?www.21cnjy.com?)
A.一处
B.二处
C.三处
D.四处
解:作直线l1、l2、l3所围成的三角形的外
(?http:?/??/?www.21cnjy.com?)角平分线和内角平分线,外角平分线相交于点P1、P2、P3,内角平分线相交于点P4,根据角平分线的性质可得到这4个点到三条公路的距离分别相等.
答案:D.
(?http:?/??/?www.21cnjy.com?)
2.(2021?青海)如图,在四边形ABCD中,∠A=90°,AD=3,BC=5,对角线BD平分∠ABC,则△BCD的面积为( )
(?http:?/??/?www.21cnjy.com?)
A.8
B.7.5
C.15
D.无法确定
解:过D点作DE⊥BC于E,如图,
∵BD平分∠ABC,DE⊥BC,DA⊥AB,
∴DE=DA=3,
∴△BCD的面积=×5×3=7.5.
答案:B.
(?http:?/??/?www.21cnjy.com?)
3.(2021?贵阳模拟)如图,在△ABC
(?http:?/??/?www.21cnjy.com?)中,∠C=90°,BC=1,AC=2,BD是∠ABC的平分线,设△ABD,△BCD的面积分别是S1,S2,则S1:S2等于( )
(?http:?/??/?www.21cnjy.com?)
A.2:1
B.:1
C.3:2
D.2:
解:过D作DE⊥AB于E,则DE=DC
(?http:?/??/?www.21cnjy.com?)
又∠C=90°,BC=1,AC=2,
∴AB==,
∴S1:S2=AB:BC=:1.
答案:B.
4.(2021?茂名模拟)
(?http:?/??/?www.21cnjy.com?)如图,已知点O为△ABC的两条角平分线的交点,过点O作OD⊥BC,垂足为D,且OD=4.若△ABC的面积是34,则△ABC的周长为( )
(?http:?/??/?www.21cnjy.com?)
A.8.5
B.15
C.17
D.34
解:∵点O为△ABC的两条角平分线的交点,
∴点O到△ABC各边的距离相等,
而OD⊥BC,OD=4,
∴点O到△ABC各边的距离为4,
∵S△ABC=S△AOB+S△BOC+S△AOC,
∴×AB×4+×AC×4+×BC×4=34,
∴AB+AC+BC=17,
即△ABC的周长为17.
答案:C.
5.(2021?西安模拟)如图,在△ABC中
(?http:?/??/?www.21cnjy.com?),∠B=30°,∠C=45°,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E.若DE=1,则BC的长为( )
(?http:?/??/?www.21cnjy.com?)
A.2+
B.+
C.2+
D.3
解:过点D作DF⊥AC于F,如图所示,
∵AD为∠BAC的平分线,且DE⊥AB于E,DF⊥AC于F,
∴DE=DF=1,
在Rt△BED中,∠B=30°,
∴BD=2DE=2,
在Rt△CDF中,∠C=45°,
∴△CDF为等腰直角三角形,
∴CD=DF=,
∴BC=BD+CD=2,
答案:A.
(?http:?/??/?www.21cnjy.com?)
6.(2021?湖州模拟)如图,已知
(?http:?/??/?www.21cnjy.com?)在四边形ABCD中,∠BCD=90°,BD平分∠ABC,AB=6,BC=9,CD=4,则四边形ABCD的面积是( )21·世纪
教育网
(?http:?/??/?www.21cnjy.com?)
A.24
B.30
C.36
D.42
解:过D作DH⊥AB交BA的延长线于H,
∵BD平分∠ABC,∠BCD=90°,
∴DH=CD=4,
∴四边形ABCD的面积=S△ABD+S△BCD=AB?DH+BC?CD=×6×4+×9×4=30,
答案:B.
(?http:?/??/?www.21cnjy.com?)
7.(2021?阜阳模拟)如图,在四边形AB
(?http:?/??/?www.21cnjy.com?)DC中,∠B=∠D=90°,∠BAC与∠ACD的平分线交于点O,且点O在线段BD上,BD=4,则点O到边AC的距离是( )【来源:21·世纪·教育·网】
(?http:?/??/?www.21cnjy.com?)
A.1
B.1.5
C.2
D.3
解:过O作OE⊥AC于E,
∵∠B=∠D=90°,∠BAC与∠ACD的平分线交于点O,
∴OB=OE=OD,
∵BD=4,
∴OB=OE=OD=2,
∴点O到边AC的距离是2,
答案:C.
(?http:?/??/?www.21cnjy.com?)
8.(2021?泰安模拟)如图,△ABC的外
(?http:?/??/?www.21cnjy.com?)角∠ACD的平分线CP与内角∠ABC的平分线BP交于点P,若∠BPC=40°,则∠CAP=( )21
cnjy
com
(?http:?/??/?www.21cnjy.com?)
A.40°
B.45°
C.50°
D.60°
解:延长BA,作PN⊥BD,PF⊥BA,PM⊥AC,
设∠PCD=x°,
∵CP平分∠ACD,
∴∠ACP=∠PCD=x°,PM=PN,
∵BP平分∠ABC,
∴∠ABP=∠PBC,PF=PN,
∴PF=PM,
∵∠BPC=40°,
∴∠ABP=∠PBC=∠PCD﹣∠BPC=(x﹣40)°,
∴∠BAC=∠ACD﹣∠ABC=2x°﹣(x°﹣40°)﹣(x°﹣40°)=80°,
∴∠CAF=100°,
在Rt△PFA和Rt△PMA中,
,
∴Rt△PFA≌Rt△PMA(HL),
∴∠FAP=∠PAC=50°.
答案:C.
(?http:?/??/?www.21cnjy.com?)
9.(2021?郑州模拟)如图,已知P是∠
(?http:?/??/?www.21cnjy.com?)AOB的角平分线上的一点,∠AOB=60°,PD⊥OA,M是OP的中点,点C是OB上的一个动点,若PC的最小值为3cm,则MD的长度为( )
(?http:?/??/?www.21cnjy.com?)
A.3cm
B.3cm
C.2cm
D.2cm
解:作PC⊥OB于C,则此时PC最小,
∵P是∠AOB的角平分线上的一点,PD⊥OA,PC⊥OB,
∴PD=PC=3,∠AOP=30°,
∴OP=2PD=6,
∵PD⊥OA,M是OP的中点,
∴DM=OP=3,
答案:A.
(?http:?/??/?www.21cnjy.com?)
10.(2021?西安模拟)如图
(?http:?/??/?www.21cnjy.com?),在△ABC中,∠BAC=90°,AD是BC边上的高,BE是AC边的中线,CF是∠ACB的角平分线,CF交AD于点G,交BE于点H,下面说法正确的是( )
①△ABE的面积=△BCE的面积;②∠FAG=∠FCB;③AF=AG;④BH=CH.
(?http:?/??/?www.21cnjy.com?)
A.①②③④
B.①②③
C.②④
D.①③
解:∵BE是AC边的中线,
∴AE=CE,
∵△ABE的面积=,△BCE的面积=AB,
∴△ABE的面积=△BCE的面积,故①正确;
∵AD是BC边上的高,
∴∠ADC=90°,
∵∠BAC=90°,
∴∠DAC+∠ACB=90°,∠FAG+∠DAC=90°,
∴∠FAG=∠ACB,
∵CF是∠ACB的角平分线,
∴∠ACF=∠FCB,∠ACB=2∠FCB,
∴∠FAG=2∠FCB,故②错误;
∵在△ACF和△DGC中,∠BAC=∠ADC=90°,∠ACF=∠FCB,
∴∠AFG=180°﹣∠BAC﹣∠ACF,∠AGF=∠DGC=180°﹣∠ADC﹣∠FCB,
∴∠AFG=∠AGF,
∴AF=AG,故③正确;
根据已知不能推出∠HBC=∠HCB,即不能推出HB=HC,故④错误;
即正确的为①③,
答案:D.
(?http:?/??/?www.21cnjy.com?)
二、填空题
11.(2021?襄阳模拟)如图
(?http:?/??/?www.21cnjy.com?),已知△ABC的周长是32,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=6,△ABC的面积是 96 .
(?http:?/??/?www.21cnjy.com?)
解:过O作OM⊥AB,ON⊥AC,连接AO,
∵OB,OC分别平分∠ABC和∠ACB,
∴OM=ON=OD=6,
∴△ABC的面积为:×AB×OM+BC×DO+NO=(AB+BC+AC)×DO=32×6=96.
答案:96.
(?http:?/??/?www.21cnjy.com?)
12.(2021?合肥模拟)如图,
(?http:?/??/?www.21cnjy.com?)四边形ABCD中,AB⊥AD,点E是BC边的中点,DA平分对角线BD与CD边延长线的夹角,若BD=5,CD=7,则AE= 6 .
(?http:?/??/?www.21cnjy.com?)
解:如图,
(?http:?/??/?www.21cnjy.com?)
取BD中点H,连AH、EH,
∵AB⊥AD,
∴AH=DH=BH=BD=2.5,
∴∠HDA=∠HAD,
∵DA平分∠FDB,
∴∠FDA=∠HDA,
∴∠FDA=∠HAD,
∴AH∥DF,
∵点E是BC边的中点,点H是BD的中点,
∴EH∥CD,EH=CD=3.5,
∴A、H、E三点共线,
∴AE=AH+EH=2.5+3.5=6.
13.(2021?株洲模拟)在△ABC中,若其内部的点P满足∠APB=∠BPC=∠CPA=120°,则称P为△ABC的费马点.如图所示,在△ABC中,已知∠BAC=45°,设P为△ABC的费马点,且满足∠PBA=45°,PA=4,则△PAC的面积为 4 .2-1-c-n-j-y
(?http:?/??/?www.21cnjy.com?)
解:如图,延长BP交AC于D,
(?http:?/??/?www.21cnjy.com?)
∵∠BAC=∠PBA=45°,
∴∠ADB=90°,AD=BD,
∵P为△ABC的费马点,
∴∠APB=∠CPA=120°,
∴∠BAP=180°﹣120°﹣45°=15°,
∴∠PAC=45°﹣15°=30°,
∴∠APD=60°,
Rt△PAD中,∵PA=4,
∴PD=2,AD=2,
∵∠APC=120°,
∴∠CPD=120°﹣60°=60°,
Rt△PDC中,∠PCD=30°,
∴CD=2,
∴AC=AD+CD=2+2=4,
∴△PAC的面积为==4.
答案:4.
14.(2021?衡水模拟)如图,△ABC中,BD平分∠ABC,交AC于D,DE⊥AB于点E,△ABC的面积是42cm2,AB=10cm,BC=14cm,则DE= cm.21教育名师原创作品
(?http:?/??/?www.21cnjy.com?)
解:作DF⊥BC于F,如图,
∵BD平分∠ABC,DE⊥AB,DF⊥BC,
∴DE=DF,
∵S△ADB+S△BCD=S△ABC,
∴×10×DE+×14×DF=42,
∴5DE+7DE=42,
∴DE=(cm).
答案:.
(?http:?/??/?www.21cnjy.com?)
15.(2020?牡丹江)已知如图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC,∠CED=35°,则∠EAB是 35 度.
(?http:?/??/?www.21cnjy.com?)
解:过点E作EF⊥AD,
∵DE平分∠ADC,且E是BC的中点,
∴CE=EB=EF,
又∵∠B=90°,且AE=AE,
∴△ABE≌△AFE,
∴∠EAB=∠EAF.
又∵∠CED=35°,∠C=90°,
∴∠CDE=90°﹣35°=55°,
∴∠CDA=110°,
∵∠B=∠C=90°,
∴DC∥AB,
∴∠CDA+∠DAB=180°,
∴∠DAB=70°,
∴∠EAB=35°.
答案:35.
(?http:?/??/?www.21cnjy.com?)
16.(2021?贵阳模拟)如图,在△B
(?http:?/??/?www.21cnjy.com?)CD中,∠BDC=90°,以BD为斜边,向外作Rt△ABD.若AD=4,∠ADB=∠C.且P是BC边上一动点,则DP长的最小值为 4 .21世纪教育网版权所有
(?http:?/??/?www.21cnjy.com?)
解:∵∠BDC=90°,∠A=90°,
∴∠ABD+∠ADB=90°,
∠C+∠CBD=90°,
∵∠ADB=∠C,
∴∠ABD=∠CBD,
由垂线段最短可知DP⊥BC时DP的长度最小,
此时,DP=AD,
∵AD=4,
∴DP的最小值为4.
答案:4.
(?http:?/??/?www.21cnjy.com?)
三、解答题
17.(2021?上海模拟)
(?http:?/??/?www.21cnjy.com?)如图,△ABC中,∠B的平分线BD与∠C的外角平分线CE交于点P.求证:点P到三边AB、BC、CA所在的直线的距离相等.【来源:21cnj
y.co
m】
(?http:?/??/?www.21cnjy.com?)
证明:如图,过点P作三边AB、BC、CA所在直线的垂线,垂足分别是Q、M、N.
则垂线段PQ、PM、PN,即为P点到三边AB、BC、CA所在直线的距离.
∵P是∠ABC的平分线BD上的一点,
∴PM=PQ.
∵P是∠ACM的平分线CE上的一点,
∴PM=PN.
∴PQ=PM=PN.
∴P点到三边AB、BC、CA所在直线的距离相等.
(?http:?/??/?www.21cnjy.com?)
18.(2021?北京模拟)如图,已知∠BAC=90°,AD⊥BC于点D,∠1=∠2,EF∥BC交AC于点F.试说明AE=CF.
(?http:?/??/?www.21cnjy.com?)【版权所有:21教育】
解:作EH⊥AB于H,作FG⊥BC于G,
∵∠1=∠2,AD⊥BC,
∴EH=ED(角平分线的性质)
∵EF∥BC,AD⊥BC,FG⊥BC,
∴四边形EFGD是矩形,
∴ED=FG,
∴EH=FG,
∵∠BAD+∠CAD=90°,∠C+∠CAD=90°,
∴∠BAD=∠C,
又∵∠AHE=∠FGC=90°,
∴△AEH≌△CFG(AAS)
∴AE=CF.
(?http:?/??/?www.21cnjy.com?)
19.(2020?北京模拟)已知:如图,四边形ABCD中,对角线AC,BD相交于点O,AB=AC=AD,∠DAC=∠ABC.21
cnjy
com
(1)求证:BD平分∠ABC;
(2)若∠DAC=45°,OA=1,求OC的长.
(?http:?/??/?www.21cnjy.com?)
(1)证明:∵AB=AC,
∴∠ABC=∠ACB,
∵∠DAC=∠ABC,
∴∠DAC=∠ACB.
∴AD∥BC,
∴∠ADB=∠CBD.
又∵AB=AD,
∴∠ADB=∠ABD.
∴∠ABD=∠CBD.
∴BD平分∠ABC;
(2)解:过点O作OE⊥BC于E,
∵∠DAC=45°,∠DAC=∠ABC,
∴∠ABC=∠ACB=45°,
∴∠B
AC=90°,
∵BD平分∠ABC,
∴OE=OA=1.
在Rt△OEC中,∠ACB=45°,OE=1,
∴OC=.
(?http:?/??/?www.21cnjy.com?)
20.(2021?龙岩模拟)观察、猜想、探究:
在△ABC中,∠ACB=2∠B.
(1)如图①,当∠C=90°,AD为∠BAC的角平分线时,求证:AB=AC+CD;
(2)如图②,当∠C≠90°,AD为∠BAC的角平分线时,线段AB、AC、CD又有怎样的数量关系?不需要证明,请直接写出你的猜想;
(3)如图③,当AD为△ABC的外角平分线时,线段AB、AC、CD又有怎样的数量关系?请写出你的猜想,并对你的猜想给予证明.
(?http:?/??/?www.21cnjy.com?)
(?http:?/??/?www.21cnjy.com?)
解:(1)过D作DE⊥AB,交AB于点E,如图1所示,
∵AD为∠BAC的平分线,DC⊥AC,DE⊥AB,
∴DE=DC,
在Rt△ACD和Rt△AED中,
AD=AD,DE=DC,
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE,∠ACB=∠AED,
∵∠ACB=2∠B,
∴∠AED=2∠B,
又∵∠AED=∠B+∠EDB,
∴∠B=∠EDB,
∴BE=DE=DC,
则AB=BE+AE=CD+AC;
(2)AB=CD+AC,理由为:
在AB上截取AG=AC,如图2所示,
∵AD为∠BAC的平分线,
∴∠GAD=∠CAD,
∵在△ADG和△ADC中,
,
∴△ADG≌△ADC(SAS),
∴CD=DG,∠AGD=∠ACB,
∵∠ACB=2∠B,
∴∠AGD=2∠B,
又∵∠AGD=∠B+∠GDB,
∴∠B=∠GDB,
∴BE=DG=DC,
则AB=BG+AG=CD+AC;
(3)AB=CD﹣AC,理由为:
在AF上截取AG=AC,如图3所示,
∵AD为∠FAC的平分线,
∴∠GAD=∠CAD,
∵在△ADG和△ACD中,
,
∴△ADG≌△ACD(SAS),
∴CD=GD,∠AGD=∠ACD,即∠ACB=∠FGD,
∵∠ACB=2∠B,
∴∠FGD=2∠B,
又∵∠FGD=∠B+∠GDB,
∴∠B=∠GDB,
∴BG=DG=DC,
则AB=BG﹣AG=CD﹣AC.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
