【人教版八上高频易错必刷题】13.1 轴对称(含解析)
文档属性
| 名称 | 【人教版八上高频易错必刷题】13.1 轴对称(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-18 18:24:06 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
13.1
轴对称
高频易错必刷题汇编
一、选择题
1.(2021?岳阳)下列品牌的标识中,是轴对称图形的是( )
A.
(?http:?/??/?www.21cnjy.com?)
B.
(?http:?/??/?www.21cnjy.com?)
C.
(?http:?/??/?www.21cnjy.com?)
D.
(?http:?/??/?www.21cnjy.com?)
2.(2021?梧州)如图,DE是△ABC的
(?http:?/??/?www.21cnjy.com?)边BC的垂直平分线,分别交边AB,BC于点D,E,且AB=9,AC=6,则△ACD的周长是( )21世纪教育网版权所有
(?http:?/??/?www.21cnjy.com?)
A.10.5
B.12
C.15
D.18
3.(2021?河北)如图,直线l,m相交于
(?http:?/??/?www.21cnjy.com?)点O.P为这两直线外一点,且OP=2.8.若点P关于直线l,m的对称点分别是点P1,P2,则P1,P2之间的距离可能是( )21教育网
(?http:?/??/?www.21cnjy.com?)
A.0
B.5
C.6
D.7
4.(2021?南充模拟)如图,每个小三角形都是等边三角形,再将1个小三角形涂黑,使4个小三角形构成轴对称图形.不同涂法有( )www.21-cn-jy.com
(?http:?/??/?www.21cnjy.com?)
A.2种
B.3种
C.4种
D.6种
5.(2021?广州模拟)
(?http:?/??/?www.21cnjy.com?)如图,在Rt△ABC中,∠C=90°,AB边的垂直平分线DE交BC于点D,交AB于点E,连接AD,AD将∠CAB分成两个角,且∠CAD:∠BAD=2:5,则∠ADC的度数是( )
(?http:?/??/?www.21cnjy.com?)
A.70°
B.75°
C.80°
D.85°
6.(2021?天津模拟)如图,△ABC中,
(?http:?/??/?www.21cnjy.com?)AB=AC,D是BC的中点,AC的垂直平分线分别交AC、AD、AB于点E、O、F,则图中全等三角形的对数是( )2·1·c·n·j·y
(?http:?/??/?www.21cnjy.com?)
A.1对
B.2对
C.3对
D.4对
7.(2021?苏州模拟)如图,A
(?http:?/??/?www.21cnjy.com?)C,BD在AB的同侧,AC=2,BD=8,AB=8,M为AB的中点.若∠CMD=120°,则CD长的最大值是( )21·世纪
教育网
(?http:?/??/?www.21cnjy.com?)
A.12
B.4
C.4
D.14
8.(2021?宝鸡模拟)如图,在△A
(?http:?/??/?www.21cnjy.com?)BC中,∠A=60°,∠ABC=45°,BD平分∠ABC交AC于点D,BD的垂直平分线EF交AB于点E,交BC于点F,若AD=10,则AE的长为( )2-1-c-n-j-y
(?http:?/??/?www.21cnjy.com?)
A.5+5
B.5
C.5+6
D.6
9.(2021?西安模拟)如图,将△ABC放
(?http:?/??/?www.21cnjy.com?)在每个小正方形边长均为1的网格中,点A、B、C均落在格点上,若点B的坐标为(2,﹣1),则到△ABC三个顶点距离相等的点的坐标为( )21
cnjy
com
(?http:?/??/?www.21cnjy.com?)
A.(0,1)
B.(3,1)
C.(1,﹣1)
D.(0,0)
10.(2021?南充模拟)如图,在△ABC中,∠A=90°,∠C=30°,PQ垂直平分BC,与AC交于点P,下列结论正确的是( )
(?http:?/??/?www.21cnjy.com?)
A.PC<2PA
B.PC>2PA
C.AB<2PA
D.AB>2PA
二、填空题
11.(2021?哈尔滨模拟)在△ABC中,∠ABC=45°,AB=2,AB边的垂直平分线交AB于D,交直线BC于点E,若CE=1,则线段DC的长为
.
12.(2021?株洲模拟)如图,已知
(?http:?/??/?www.21cnjy.com?)直线m是正五边形ABCDE的对称轴,且直线m过点D,直线m与对角线BE相交于点O,则∠AOE=
度.
(?http:?/??/?www.21cnjy.com?)
13.(2021?枣庄模拟)如
(?http:?/??/?www.21cnjy.com?)图,在矩形ABCD中,AB=8,BC=4,一发光电子开始置于AB边的点P处,并设定此时为发光电子第一次与矩形的边碰撞,将发光电子沿着PR方向发射,碰撞到矩形的边时均反射,每次反射的反射角和入射角都等于45°,当发光电子与矩形的边碰撞2020次后,它与AB边的碰撞次数是
.
(?http:?/??/?www.21cnjy.com?)
14.(2021?沈阳模拟)
(?http:?/??/?www.21cnjy.com?)如图,在△ABC中,∠A=45°,∠B=60°,AB=4,P是BC边上的动点(不与B,C重合),点P关于直线AB,AC的对称点分别为M,N,则线段MN长的取值范围是
.
(?http:?/??/?www.21cnjy.com?)
15.(2021?西安模拟)如图,已知正方
(?http:?/??/?www.21cnjy.com?)形ABCD的边长为5,l是过点A的任意一条直线,点M是点D关于直线l的对称点.连接CM,则线段CM长度的最大值是
.
(?http:?/??/?www.21cnjy.com?)
16.(2021?延边模拟)如图,∠AO
(?http:?/??/?www.21cnjy.com?)B=40°,点P在∠AOB的内部,点C,D分别是点P关于直线OA,OB的对称点,连接CD分别交OA,OB于点E、F.则∠EPF=
.
(?http:?/??/?www.21cnjy.com?)
三、解答题
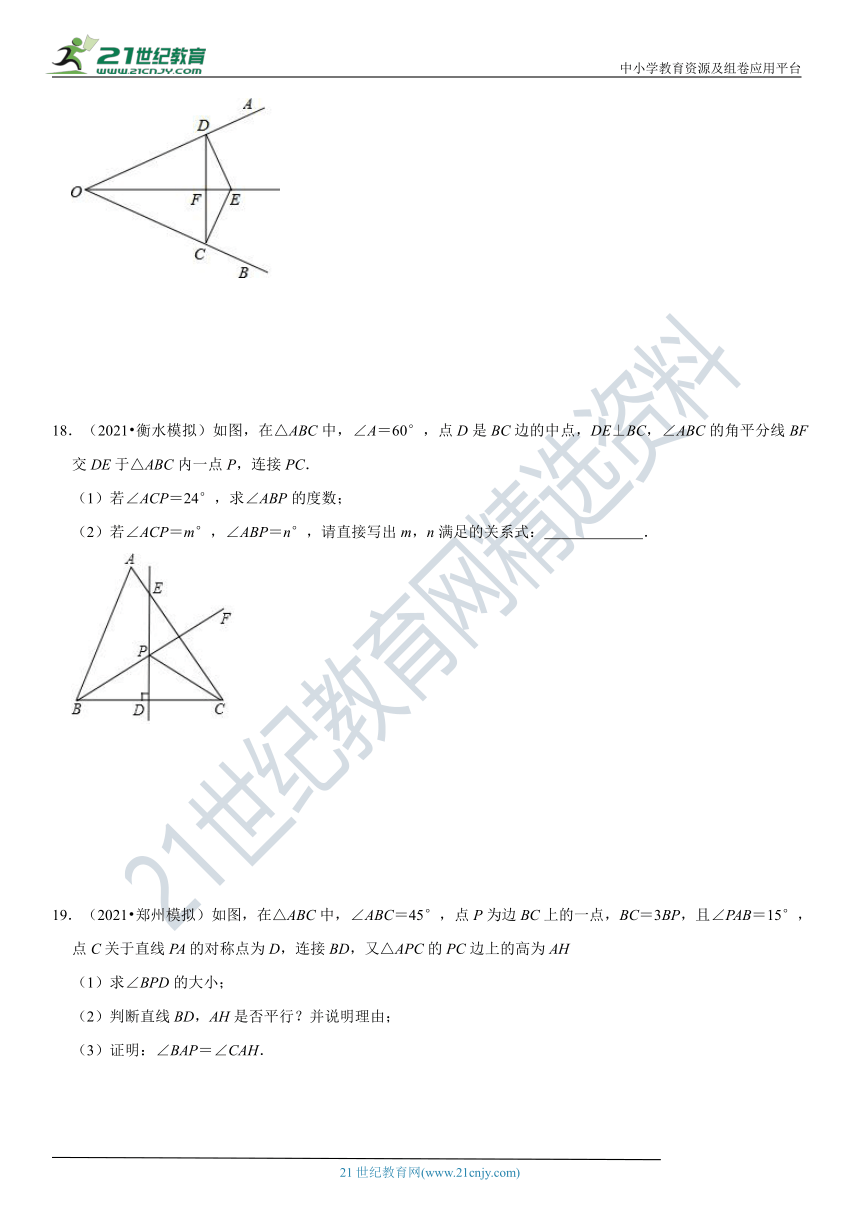
17.(2021?石家庄模拟)如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD,且交OE于点F.
(1)求证:OE是CD的垂直平分线.
(2)若∠AOB=60°,请你探究OE,EF之间有什么数量关系?并证明你的结论.
(?http:?/??/?www.21cnjy.com?)
18.(2021?衡水模拟)如
(?http:?/??/?www.21cnjy.com?)图,在△ABC中,∠A=60°,点D是BC边的中点,DE⊥BC,∠ABC的角平分线BF交DE于△ABC内一点P,连接PC.
(1)若∠ACP=24°,求∠ABP的度数;
(2)若∠ACP=m°,∠ABP=n°,请直接写出m,n满足的关系式:
.
(?http:?/??/?www.21cnjy.com?)
19.(2021?郑州模拟)如图,在△AB
(?http:?/??/?www.21cnjy.com?)C中,∠ABC=45°,点P为边BC上的一点,BC=3BP,且∠PAB=15°,点C关于直线PA的对称点为D,连接BD,又△APC的PC边上的高为AH【版权所有:21教育】
(1)求∠BPD的大小;
(2)判断直线BD,AH是否平行?并说明理由;
(3)证明:∠BAP=∠CAH.
(?http:?/??/?www.21cnjy.com?)
20.(2021?钦州模拟
(?http:?/??/?www.21cnjy.com?))如图,在△ABC中,AB边的垂直平分线l1交BC于点D,AC边的垂直平分线l2交BC于点E,l1与l2相交于点O,连接OB,OC,若△ADE的周长为6cm,△OBC的周长为16cm.
(1)求线段BC的长;
(2)连接OA,求线段OA的长;
(3)若∠BAC=120°,求∠DAE的度数.
(?http:?/??/?www.21cnjy.com?)
13.1
轴对称
高频易错必刷题汇编
一、选择题
1.(2021?岳阳)下列品牌的标识中,是轴对称图形的是( )
A.
(?http:?/??/?www.21cnjy.com?)
B.
(?http:?/??/?www.21cnjy.com?)
C.
(?http:?/??/?www.21cnjy.com?)
D.
(?http:?/??/?www.21cnjy.com?)
解:A.是轴对称图形,故此选项符合题意;
B.不是轴对称图形,故此选项不合题意;
C.不是轴对称图形,故此选项不合题意;
D.不是轴对称图形,故此选项不合题意;
答案:A.
2.(2021?梧州)如图,DE是
(?http:?/??/?www.21cnjy.com?)△ABC的边BC的垂直平分线,分别交边AB,BC于点D,E,且AB=9,AC=6,则△ACD的周长是( )【来源:21·世纪·教育·网】
(?http:?/??/?www.21cnjy.com?)
A.10.5
B.12
C.15
D.18
解:∵DE是△ABC的边BC的垂直平分线,
∴DB=DC,
∴△ACD的周长=AD+AC+CD=AD+BD+AC=AB+AC,
∵AB=9,AC=6,
∴△ACD的周长=9+6=15,
答案:C.
3.(2021?河北)如图,直
(?http:?/??/?www.21cnjy.com?)线l,m相交于点O.P为这两直线外一点,且OP=2.8.若点P关于直线l,m的对称点分别是点P1,P2,则P1,P2之间的距离可能是( )
(?http:?/??/?www.21cnjy.com?)
A.0
B.5
C.6
D.7
解:连接OP1,OP2,P1P2,
∵点P关于直线l,m的对称点分别是点P1,P2,
∴OP1=OP=2.8,OP=OP2=2.8,
OP1+OP2≥P1P2,
0<P1P2≤5.6,
(?http:?/??/?www.21cnjy.com?)
答案:B.
4.(2021?南充模拟)如图,每个小三角形都是等边三角形,再将1个小三角形涂黑,使4个小三角形构成轴对称图形.不同涂法有( )
(?http:?/??/?www.21cnjy.com?)
A.2种
B.3种
C.4种
D.6种
解:如图所示,满足题意的涂色方式有4种,
(?http:?/??/?www.21cnjy.com?)
答案:C.
5.(2021?广州模拟)如图,在
(?http:?/??/?www.21cnjy.com?)Rt△ABC中,∠C=90°,AB边的垂直平分线DE交BC于点D,交AB于点E,连接AD,AD将∠CAB分成两个角,且∠CAD:∠BAD=2:5,则∠ADC的度数是( )
(?http:?/??/?www.21cnjy.com?)
A.70°
B.75°
C.80°
D.85°
解:设∠CAD=2x°,∠BAD=5x°,
∵AB的垂直平分线是DE,
∴BD=AD,
∴∠BAD=∠B,
即∠B=5x°,
∵∠C=90°,
∴∠CAB+∠B=90°,
∴2x+5x+5x=90,
解得:x=,
即∠B=∠BAD=()°,
∴∠ADC=∠B+∠BAD=()°+()°=75°,
答案:B.
(?http:?/??/?www.21cnjy.com?)
6.(2021?天津模拟)如图,△ABC中,
(?http:?/??/?www.21cnjy.com?)AB=AC,D是BC的中点,AC的垂直平分线分别交AC、AD、AB于点E、O、F,则图中全等三角形的对数是( )21·cn·jy·com
(?http:?/??/?www.21cnjy.com?)
A.1对
B.2对
C.3对
D.4对
解:∵EF是AC的垂直平分线,
∴OA=OC,
又∵OE=OE,
∴Rt△AOE≌Rt△COE,
∵AB=AC,D是BC的中点,
∴AD⊥BC,
∴△ABC关于直线AD轴对称,
∴△AOC≌△AOB,△BOD≌△COD,△ABD≌△ACD,
综上所述,全等三角形共有4对.
答案:D.
7.(2021?苏州模拟)
(?http:?/??/?www.21cnjy.com?)如图,AC,BD在AB的同侧,AC=2,BD=8,AB=8,M为AB的中点.若∠CMD=120°,则CD长的最大值是( )21教育名师原创作品
(?http:?/??/?www.21cnjy.com?)
A.12
B.4
C.4
D.14
解:如图,作点A关于CM的对称点A′,点B关于DM的对称点B′,连接CA'、MA'、MB'、A'B'、B'D,
(?http:?/??/?www.21cnjy.com?)
∵∠CMD=120°,
∴∠AMC+∠DMB=60°,
∴∠CMA′+∠DMB′=60°,
∴∠A′MB′=60°,
∵MA′=MB′,
∴△A′MB′为等边三角形
∵CD≤CA′+A′B′+B′D=CA+AM+BD=2+4+8=14,
∴CD的最大值为14,
答案:D.
8.(2021?宝鸡模拟)如图,在△A
(?http:?/??/?www.21cnjy.com?)BC中,∠A=60°,∠ABC=45°,BD平分∠ABC交AC于点D,BD的垂直平分线EF交AB于点E,交BC于点F,若AD=10,则AE的长为( )
(?http:?/??/?www.21cnjy.com?)
A.5+5
B.5
C.5+6
D.6
解:过D点作DH⊥AB于H,连接DE,如图,
∵EF垂直平分BD,
∴EB=ED,
∴∠EBD=∠EDB,
∵BD平分∠ABC,
∴∠EBD=∠CBD,
∴∠EDB=∠CBD,
∴DE∥BC,
∴∠DEA=∠ABC=45°,
在Rt△ADH中,∵∠A=60°,
∴AH=AD=×10=5,
∴DH=AH=5,
在Rt△DHE中,∵∠HED=45°,
∴HE=DH=5,
∴AE=AH+EH=5+5.
答案:A.
(?http:?/??/?www.21cnjy.com?)
9.(2021?西安模拟)
(?http:?/??/?www.21cnjy.com?)如图,将△ABC放在每个小正方形边长均为1的网格中,点A、B、C均落在格点上,若点B的坐标为(2,﹣1),则到△ABC三个顶点距离相等的点的坐标为( )
(?http:?/??/?www.21cnjy.com?)
A.(0,1)
B.(3,1)
C.(1,﹣1)
D.(0,0)
解:平面直角坐标系如图所示,AB与AC的垂直平分线的交点为点O,
∴到△ABC三个顶点距离相等的点的坐标为(0,0),
(?http:?/??/?www.21cnjy.com?)
答案:D.
10.(2021?南充模拟)如图,在△ABC中,∠A=90°,∠C=30°,PQ垂直平分BC,与AC交于点P,下列结论正确的是( )
(?http:?/??/?www.21cnjy.com?)
A.PC<2PA
B.PC>2PA
C.AB<2PA
D.AB>2PA
解:连接BP,
∵∠A=90°,∠C=30°,
∴∠ABC=60°,
∵PQ垂直平分BC,
∴PB=PC,
∴∠PBC=∠C=30°,
∴∠ABP=30°,
∴AP=BP=PC,
∴PC=2PA,故A、B选项错误;
∵∠A=90°,
∴AB<PB<2PA,
∴C正确,D错误;
答案:C.
(?http:?/??/?www.21cnjy.com?)
二、填空题
11.(2021?哈尔滨模拟)在△ABC中,∠ABC=45°,AB=2,AB边的垂直平分线交AB于D,交直线BC于点E,若CE=1,则线段DC的长为 1或 .
解:当E点在线段BC上时,
如图,过点D作DF⊥BC,垂足为F,
∵线段AB的垂直平分线交直线BC于点E,
∴AE=BE,
∴∠BAE=∠ABC=45°,
∴∠AEB=90°,
∵∠ABC=45°,∠BDE=90°,
∴∠BED=45°,
∴BD=ED,
∵AB=2,
∴BD=DE=,
∴BE==2,
∵BD=DE,DF⊥BE,
∴EF=BE=1,
∴DF=EF=1,
∵CE=1,
∴CF=2,
在Rt△CDF中,根据勾股定理得:
CD==;
当点E在BC的延长线上时,
如图,∵线段AB的垂直平分线交直线BC于点E,
∵∠ABC=45°,AB=2
,
由(1)同理可得:BE=2,
∵CE=1,
∴BC=1,
如图,过点C作CF⊥AB,垂足为F,
∴BF=CF==,
∴DF=,
在Rt△CDF中,由勾股定理得:
CD=,
综上:CD=1或,
(?http:?/??/?www.21cnjy.com?)
答案:1或.
(?http:?/??/?www.21cnjy.com?)
12.(2021?株洲模拟)如图,
(?http:?/??/?www.21cnjy.com?)已知直线m是正五边形ABCDE的对称轴,且直线m过点D,直线m与对角线BE相交于点O,则∠AOE= 72 度.【来源:21cnj
y.co
m】
(?http:?/??/?www.21cnjy.com?)
解:∵ABCDE是正五边形,
∴∠EAB=108°,
∵AE=AB,
∴∠AEB=∠ABE=36°,
∵直线m垂直平分线段AB,
∴OA=OB,
∴∠OAB=∠OBA=36°,
∴∠AOE=∠OAB+∠OBA=72°,
答案:72;
(?http:?/??/?www.21cnjy.com?)
13.(2021?枣庄模拟)如图,在矩形A
(?http:?/??/?www.21cnjy.com?)BCD中,AB=8,BC=4,一发光电子开始置于AB边的点P处,并设定此时为发光电子第一次与矩形的边碰撞,将发光电子沿着PR方向发射,碰撞到矩形的边时均反射,每次反射的反射角和入射角都等于45°,当发光电子与矩形的边碰撞2020次后,它与AB边的碰撞次数是 674 .
(?http:?/??/?www.21cnjy.com?)
解:如图以AB为x轴,AD为y轴,建立平面直角坐标系,
(?http:?/??/?www.21cnjy.com?)
根据图形可以得到:每6次反弹为一个循环组依次循环,经过6次反弹后动点回到出发点(6,0),且每次循环它与AB边的碰撞有2次,
∵2020÷6=336…4,
当点P第2020次碰到矩形的边时为第336个循环组的第4次反弹,点P的坐标为(2,0),
∴它与AB边的碰撞次数是=336×2+2=674(次),
答案:674.
14.(2021?沈阳模拟)如图,在△ABC中,∠A=45°,∠B=60°,AB=4,P是BC边上的动点(不与B,C重合),点P关于直线AB,AC的对称点分别为M,N,则线段MN长的取值范围是 2≤MN<4 .
(?http:?/??/?www.21cnjy.com?)
解:连接AM、AN、AP,如图所示.
∵点P关于直线AB,AC的对称点分别为M,N,
∴AM=AP=AN,∠MAB=∠PAB,∠NAC=∠PAC,
∴△MAN等腰直角三角形,
∴MN=AM=AP,
∴2≤AP<4,
∴2≤MN<4.
答案:2≤MN<4.
(?http:?/??/?www.21cnjy.com?)
15.(2021?西安模拟)如图,已知正方形ABCD的边长为5,l是过点A的任意一条直线,点M是点D关于直线l的对称点.连接CM,则线段CM长度的最大值是 5+5 .21cnjy.com
(?http:?/??/?www.21cnjy.com?)
解:如图,连接AC,AM.
(?http:?/??/?www.21cnjy.com?)
∵四边形ABCD是正方形,
∴∠D=90°,AD=CD=5,
∴AC=5,
∵D,M关于直线l对称,
∴AM=AD=5,
∵CM≤AC+AM=5+5,
∴CM的最大值为5+5.
16.(2021?延边模拟)如图
(?http:?/??/?www.21cnjy.com?),∠AOB=40°,点P在∠AOB的内部,点C,D分别是点P关于直线OA,OB的对称点,连接CD分别交OA,OB于点E、F.则∠EPF= 100° .
(?http:?/??/?www.21cnjy.com?)
解:如图,设OA交PC于R,OB交PD于T.
(?http:?/??/?www.21cnjy.com?)
∵点C、D分别是点P关于直线OA、OB的对称点,
∴OA垂直平分PC,OB垂直平分PD,
∴CE=PE,PF=DF,
∴∠PEF=2∠C,∠PFE=2∠D,
∵∠PRE=∠PTF=90°,
∴在四边形OTPR中,
∴∠CPD+∠AOB=180°,
∵∠EPF+2∠C+2∠D=180°,
即∠CPD+∠C+∠D=180°,
∴∠C+∠D=∠AOB=40°
∴∠EPF=180°﹣40°×2=100°.
答案:100°.
三、解答题
17.(2021?石家庄模拟)如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD,且交OE于点F.【出处:21教育名师】
(1)求证:OE是CD的垂直平分线.
(2)若∠AOB=60°,请你探究OE,EF之间有什么数量关系?并证明你的结论.
(?http:?/??/?www.21cnjy.com?)
解:(1)∵E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,
∴DE=CE,OE=OE,
∴Rt△ODE≌Rt△OCE,
∴OD=OC,
∴△DOC是等腰三角形,
∵OE是∠AOB的平分线,
∴OE是CD的垂直平分线;
(2)∵OE是∠AOB的平分线,∠AOB=60°,
∴∠AOE=∠BOE=30°,
∵EC⊥OB,ED⊥OA,
∴OE=2DE,∠ODF=∠OED=60°,
∴∠EDF=30°,
∴DE=2EF,
∴OE=4EF.
18.(2021?衡水模拟)如图,在△A
(?http:?/??/?www.21cnjy.com?)BC中,∠A=60°,点D是BC边的中点,DE⊥BC,∠ABC的角平分线BF交DE于△ABC内一点P,连接PC.www-2-1-cnjy-com
(1)若∠ACP=24°,求∠ABP的度数;
(2)若∠ACP=m°,∠ABP=n°,请直接写出m,n满足的关系式: m+3n=120 .
(?http:?/??/?www.21cnjy.com?)
解:(1)∵点D是BC边的中点,DE⊥BC,
∴PB=PC,
∴∠PBC=∠PCB,
∵BP平分∠ABC,
∴∠PBC=∠ABP,
∴∠PBC=∠PCB=∠ABP,
∵∠A=60°,∠ACP=24°,
∴∠PBC+∠PCB+∠ABP=120°﹣24°,
∴3∠ABP=120°﹣24°,
∴∠ABP=32°;
(2)∵点D是BC边的中点,DE⊥BC,
∴PB=PC,
∴∠PBC=∠PCB,
∵BP平分∠ABC,
∴∠PBC=∠ABP,
∴∠PBC=∠PCB=∠ABP=n°,
∵∠A=60°,∠ACP=m°,
∴∠PBC+∠PCB+∠ABP=120°﹣m°,
∴3∠ABP=120°﹣m°,
∴3n°+m°=120°,
答案:m+3n=120.
19.(2021?郑州模拟)如图,
(?http:?/??/?www.21cnjy.com?)在△ABC中,∠ABC=45°,点P为边BC上的一点,BC=3BP,且∠PAB=15°,点C关于直线PA的对称点为D,连接BD,又△APC的PC边上的高为AH21
cnjy
com
(1)求∠BPD的大小;
(2)判断直线BD,AH是否平行?并说明理由;
(3)证明:∠BAP=∠CAH.
(?http:?/??/?www.21cnjy.com?)
解:(1)∵∠PAB=15°,∠ABC=45°,
∴∠APC=15°+45°=60°,
∵点C关于直线PA的对称点为D,
∴PD=PC,AD=AC,
∴△ADP≌△ACP,
∴∠APC=∠APD=60°,
∴∠BPD=180°﹣120°=60°;
(2)直线BD,AH平行.理由:
∵BC=3BP,
∴BP=PC=PD,
如图,取PD中点E,连接BE,则△BEP为等边三角形,△BDE为等腰三角形,
(?http:?/??/?www.21cnjy.com?)
∴∠BEP=60°,
∴∠BDE=∠BEP=30°,
∴∠DBP=90°,即BD⊥BC.
又∵△APC的PC边上的高为AH,
∴AH⊥BC,
∴BD∥AH;
(3)如图,过点A作BD、DP的垂线,垂足分别为G、F.
(?http:?/??/?www.21cnjy.com?)
∵∠APC=∠APD,即点A在∠DPC的平分线上,
∴AH=AF.
∵∠CBD=90°,∠ABC=45°,
∴∠GBA=∠CBA=45°,
即点A在∠GBC的平分线上,
∴AG=AH,
∴AG=AF,
∴点A在∠GDP的平分线上.
又∵∠BDP=30°,
∴∠GDP=150°,
∴∠ADP=×150°=75°,
∴∠C=∠ADP=75°,
∴Rt△ACH中,∠CAH=15°,
∴∠BAP=∠CAH.
20.(2021?钦州模拟)如图,
(?http:?/??/?www.21cnjy.com?)在△ABC中,AB边的垂直平分线l1交BC于点D,AC边的垂直平分线l2交BC于点E,l1与l2相交于点O,连接OB,OC,若△ADE的周长为6cm,△OBC的周长为16cm.
(1)求线段BC的长;
(2)连接OA,求线段OA的长;
(3)若∠BAC=120°,求∠DAE的度数.
(?http:?/??/?www.21cnjy.com?)
解:(1)∵l1是AB边的垂直平分线
∴DA=DB,
∵l2是AC边的垂直平分线,
∴EA=EC,
BC=BD+DE+EC=DA+DE+EA=6cm;
(2)∵l1是AB边的垂直平分线,
∴OA=OB,
∵l2是AC边的垂直平分线,
∴OA=OC,
∵OB+OC+BC=16cm,
∴OA=0B=OC=5cm;
(3)∵∠BAC=120°,
∴∠ABC+∠ACB=60°,
∵DA=DB,EA=EC,
∴∠BAD=∠ABC,∠EAC=∠ACB,
∴∠DAE=∠BAC﹣∠BAD﹣∠EAC=60°.
(?http:?/??/?www.21cnjy.com?)
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
13.1
轴对称
高频易错必刷题汇编
一、选择题
1.(2021?岳阳)下列品牌的标识中,是轴对称图形的是( )
A.
(?http:?/??/?www.21cnjy.com?)
B.
(?http:?/??/?www.21cnjy.com?)
C.
(?http:?/??/?www.21cnjy.com?)
D.
(?http:?/??/?www.21cnjy.com?)
2.(2021?梧州)如图,DE是△ABC的
(?http:?/??/?www.21cnjy.com?)边BC的垂直平分线,分别交边AB,BC于点D,E,且AB=9,AC=6,则△ACD的周长是( )21世纪教育网版权所有
(?http:?/??/?www.21cnjy.com?)
A.10.5
B.12
C.15
D.18
3.(2021?河北)如图,直线l,m相交于
(?http:?/??/?www.21cnjy.com?)点O.P为这两直线外一点,且OP=2.8.若点P关于直线l,m的对称点分别是点P1,P2,则P1,P2之间的距离可能是( )21教育网
(?http:?/??/?www.21cnjy.com?)
A.0
B.5
C.6
D.7
4.(2021?南充模拟)如图,每个小三角形都是等边三角形,再将1个小三角形涂黑,使4个小三角形构成轴对称图形.不同涂法有( )www.21-cn-jy.com
(?http:?/??/?www.21cnjy.com?)
A.2种
B.3种
C.4种
D.6种
5.(2021?广州模拟)
(?http:?/??/?www.21cnjy.com?)如图,在Rt△ABC中,∠C=90°,AB边的垂直平分线DE交BC于点D,交AB于点E,连接AD,AD将∠CAB分成两个角,且∠CAD:∠BAD=2:5,则∠ADC的度数是( )
(?http:?/??/?www.21cnjy.com?)
A.70°
B.75°
C.80°
D.85°
6.(2021?天津模拟)如图,△ABC中,
(?http:?/??/?www.21cnjy.com?)AB=AC,D是BC的中点,AC的垂直平分线分别交AC、AD、AB于点E、O、F,则图中全等三角形的对数是( )2·1·c·n·j·y
(?http:?/??/?www.21cnjy.com?)
A.1对
B.2对
C.3对
D.4对
7.(2021?苏州模拟)如图,A
(?http:?/??/?www.21cnjy.com?)C,BD在AB的同侧,AC=2,BD=8,AB=8,M为AB的中点.若∠CMD=120°,则CD长的最大值是( )21·世纪
教育网
(?http:?/??/?www.21cnjy.com?)
A.12
B.4
C.4
D.14
8.(2021?宝鸡模拟)如图,在△A
(?http:?/??/?www.21cnjy.com?)BC中,∠A=60°,∠ABC=45°,BD平分∠ABC交AC于点D,BD的垂直平分线EF交AB于点E,交BC于点F,若AD=10,则AE的长为( )2-1-c-n-j-y
(?http:?/??/?www.21cnjy.com?)
A.5+5
B.5
C.5+6
D.6
9.(2021?西安模拟)如图,将△ABC放
(?http:?/??/?www.21cnjy.com?)在每个小正方形边长均为1的网格中,点A、B、C均落在格点上,若点B的坐标为(2,﹣1),则到△ABC三个顶点距离相等的点的坐标为( )21
cnjy
com
(?http:?/??/?www.21cnjy.com?)
A.(0,1)
B.(3,1)
C.(1,﹣1)
D.(0,0)
10.(2021?南充模拟)如图,在△ABC中,∠A=90°,∠C=30°,PQ垂直平分BC,与AC交于点P,下列结论正确的是( )
(?http:?/??/?www.21cnjy.com?)
A.PC<2PA
B.PC>2PA
C.AB<2PA
D.AB>2PA
二、填空题
11.(2021?哈尔滨模拟)在△ABC中,∠ABC=45°,AB=2,AB边的垂直平分线交AB于D,交直线BC于点E,若CE=1,则线段DC的长为
.
12.(2021?株洲模拟)如图,已知
(?http:?/??/?www.21cnjy.com?)直线m是正五边形ABCDE的对称轴,且直线m过点D,直线m与对角线BE相交于点O,则∠AOE=
度.
(?http:?/??/?www.21cnjy.com?)
13.(2021?枣庄模拟)如
(?http:?/??/?www.21cnjy.com?)图,在矩形ABCD中,AB=8,BC=4,一发光电子开始置于AB边的点P处,并设定此时为发光电子第一次与矩形的边碰撞,将发光电子沿着PR方向发射,碰撞到矩形的边时均反射,每次反射的反射角和入射角都等于45°,当发光电子与矩形的边碰撞2020次后,它与AB边的碰撞次数是
.
(?http:?/??/?www.21cnjy.com?)
14.(2021?沈阳模拟)
(?http:?/??/?www.21cnjy.com?)如图,在△ABC中,∠A=45°,∠B=60°,AB=4,P是BC边上的动点(不与B,C重合),点P关于直线AB,AC的对称点分别为M,N,则线段MN长的取值范围是
.
(?http:?/??/?www.21cnjy.com?)
15.(2021?西安模拟)如图,已知正方
(?http:?/??/?www.21cnjy.com?)形ABCD的边长为5,l是过点A的任意一条直线,点M是点D关于直线l的对称点.连接CM,则线段CM长度的最大值是
.
(?http:?/??/?www.21cnjy.com?)
16.(2021?延边模拟)如图,∠AO
(?http:?/??/?www.21cnjy.com?)B=40°,点P在∠AOB的内部,点C,D分别是点P关于直线OA,OB的对称点,连接CD分别交OA,OB于点E、F.则∠EPF=
.
(?http:?/??/?www.21cnjy.com?)
三、解答题
17.(2021?石家庄模拟)如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD,且交OE于点F.
(1)求证:OE是CD的垂直平分线.
(2)若∠AOB=60°,请你探究OE,EF之间有什么数量关系?并证明你的结论.
(?http:?/??/?www.21cnjy.com?)
18.(2021?衡水模拟)如
(?http:?/??/?www.21cnjy.com?)图,在△ABC中,∠A=60°,点D是BC边的中点,DE⊥BC,∠ABC的角平分线BF交DE于△ABC内一点P,连接PC.
(1)若∠ACP=24°,求∠ABP的度数;
(2)若∠ACP=m°,∠ABP=n°,请直接写出m,n满足的关系式:
.
(?http:?/??/?www.21cnjy.com?)
19.(2021?郑州模拟)如图,在△AB
(?http:?/??/?www.21cnjy.com?)C中,∠ABC=45°,点P为边BC上的一点,BC=3BP,且∠PAB=15°,点C关于直线PA的对称点为D,连接BD,又△APC的PC边上的高为AH【版权所有:21教育】
(1)求∠BPD的大小;
(2)判断直线BD,AH是否平行?并说明理由;
(3)证明:∠BAP=∠CAH.
(?http:?/??/?www.21cnjy.com?)
20.(2021?钦州模拟
(?http:?/??/?www.21cnjy.com?))如图,在△ABC中,AB边的垂直平分线l1交BC于点D,AC边的垂直平分线l2交BC于点E,l1与l2相交于点O,连接OB,OC,若△ADE的周长为6cm,△OBC的周长为16cm.
(1)求线段BC的长;
(2)连接OA,求线段OA的长;
(3)若∠BAC=120°,求∠DAE的度数.
(?http:?/??/?www.21cnjy.com?)
13.1
轴对称
高频易错必刷题汇编
一、选择题
1.(2021?岳阳)下列品牌的标识中,是轴对称图形的是( )
A.
(?http:?/??/?www.21cnjy.com?)
B.
(?http:?/??/?www.21cnjy.com?)
C.
(?http:?/??/?www.21cnjy.com?)
D.
(?http:?/??/?www.21cnjy.com?)
解:A.是轴对称图形,故此选项符合题意;
B.不是轴对称图形,故此选项不合题意;
C.不是轴对称图形,故此选项不合题意;
D.不是轴对称图形,故此选项不合题意;
答案:A.
2.(2021?梧州)如图,DE是
(?http:?/??/?www.21cnjy.com?)△ABC的边BC的垂直平分线,分别交边AB,BC于点D,E,且AB=9,AC=6,则△ACD的周长是( )【来源:21·世纪·教育·网】
(?http:?/??/?www.21cnjy.com?)
A.10.5
B.12
C.15
D.18
解:∵DE是△ABC的边BC的垂直平分线,
∴DB=DC,
∴△ACD的周长=AD+AC+CD=AD+BD+AC=AB+AC,
∵AB=9,AC=6,
∴△ACD的周长=9+6=15,
答案:C.
3.(2021?河北)如图,直
(?http:?/??/?www.21cnjy.com?)线l,m相交于点O.P为这两直线外一点,且OP=2.8.若点P关于直线l,m的对称点分别是点P1,P2,则P1,P2之间的距离可能是( )
(?http:?/??/?www.21cnjy.com?)
A.0
B.5
C.6
D.7
解:连接OP1,OP2,P1P2,
∵点P关于直线l,m的对称点分别是点P1,P2,
∴OP1=OP=2.8,OP=OP2=2.8,
OP1+OP2≥P1P2,
0<P1P2≤5.6,
(?http:?/??/?www.21cnjy.com?)
答案:B.
4.(2021?南充模拟)如图,每个小三角形都是等边三角形,再将1个小三角形涂黑,使4个小三角形构成轴对称图形.不同涂法有( )
(?http:?/??/?www.21cnjy.com?)
A.2种
B.3种
C.4种
D.6种
解:如图所示,满足题意的涂色方式有4种,
(?http:?/??/?www.21cnjy.com?)
答案:C.
5.(2021?广州模拟)如图,在
(?http:?/??/?www.21cnjy.com?)Rt△ABC中,∠C=90°,AB边的垂直平分线DE交BC于点D,交AB于点E,连接AD,AD将∠CAB分成两个角,且∠CAD:∠BAD=2:5,则∠ADC的度数是( )
(?http:?/??/?www.21cnjy.com?)
A.70°
B.75°
C.80°
D.85°
解:设∠CAD=2x°,∠BAD=5x°,
∵AB的垂直平分线是DE,
∴BD=AD,
∴∠BAD=∠B,
即∠B=5x°,
∵∠C=90°,
∴∠CAB+∠B=90°,
∴2x+5x+5x=90,
解得:x=,
即∠B=∠BAD=()°,
∴∠ADC=∠B+∠BAD=()°+()°=75°,
答案:B.
(?http:?/??/?www.21cnjy.com?)
6.(2021?天津模拟)如图,△ABC中,
(?http:?/??/?www.21cnjy.com?)AB=AC,D是BC的中点,AC的垂直平分线分别交AC、AD、AB于点E、O、F,则图中全等三角形的对数是( )21·cn·jy·com
(?http:?/??/?www.21cnjy.com?)
A.1对
B.2对
C.3对
D.4对
解:∵EF是AC的垂直平分线,
∴OA=OC,
又∵OE=OE,
∴Rt△AOE≌Rt△COE,
∵AB=AC,D是BC的中点,
∴AD⊥BC,
∴△ABC关于直线AD轴对称,
∴△AOC≌△AOB,△BOD≌△COD,△ABD≌△ACD,
综上所述,全等三角形共有4对.
答案:D.
7.(2021?苏州模拟)
(?http:?/??/?www.21cnjy.com?)如图,AC,BD在AB的同侧,AC=2,BD=8,AB=8,M为AB的中点.若∠CMD=120°,则CD长的最大值是( )21教育名师原创作品
(?http:?/??/?www.21cnjy.com?)
A.12
B.4
C.4
D.14
解:如图,作点A关于CM的对称点A′,点B关于DM的对称点B′,连接CA'、MA'、MB'、A'B'、B'D,
(?http:?/??/?www.21cnjy.com?)
∵∠CMD=120°,
∴∠AMC+∠DMB=60°,
∴∠CMA′+∠DMB′=60°,
∴∠A′MB′=60°,
∵MA′=MB′,
∴△A′MB′为等边三角形
∵CD≤CA′+A′B′+B′D=CA+AM+BD=2+4+8=14,
∴CD的最大值为14,
答案:D.
8.(2021?宝鸡模拟)如图,在△A
(?http:?/??/?www.21cnjy.com?)BC中,∠A=60°,∠ABC=45°,BD平分∠ABC交AC于点D,BD的垂直平分线EF交AB于点E,交BC于点F,若AD=10,则AE的长为( )
(?http:?/??/?www.21cnjy.com?)
A.5+5
B.5
C.5+6
D.6
解:过D点作DH⊥AB于H,连接DE,如图,
∵EF垂直平分BD,
∴EB=ED,
∴∠EBD=∠EDB,
∵BD平分∠ABC,
∴∠EBD=∠CBD,
∴∠EDB=∠CBD,
∴DE∥BC,
∴∠DEA=∠ABC=45°,
在Rt△ADH中,∵∠A=60°,
∴AH=AD=×10=5,
∴DH=AH=5,
在Rt△DHE中,∵∠HED=45°,
∴HE=DH=5,
∴AE=AH+EH=5+5.
答案:A.
(?http:?/??/?www.21cnjy.com?)
9.(2021?西安模拟)
(?http:?/??/?www.21cnjy.com?)如图,将△ABC放在每个小正方形边长均为1的网格中,点A、B、C均落在格点上,若点B的坐标为(2,﹣1),则到△ABC三个顶点距离相等的点的坐标为( )
(?http:?/??/?www.21cnjy.com?)
A.(0,1)
B.(3,1)
C.(1,﹣1)
D.(0,0)
解:平面直角坐标系如图所示,AB与AC的垂直平分线的交点为点O,
∴到△ABC三个顶点距离相等的点的坐标为(0,0),
(?http:?/??/?www.21cnjy.com?)
答案:D.
10.(2021?南充模拟)如图,在△ABC中,∠A=90°,∠C=30°,PQ垂直平分BC,与AC交于点P,下列结论正确的是( )
(?http:?/??/?www.21cnjy.com?)
A.PC<2PA
B.PC>2PA
C.AB<2PA
D.AB>2PA
解:连接BP,
∵∠A=90°,∠C=30°,
∴∠ABC=60°,
∵PQ垂直平分BC,
∴PB=PC,
∴∠PBC=∠C=30°,
∴∠ABP=30°,
∴AP=BP=PC,
∴PC=2PA,故A、B选项错误;
∵∠A=90°,
∴AB<PB<2PA,
∴C正确,D错误;
答案:C.
(?http:?/??/?www.21cnjy.com?)
二、填空题
11.(2021?哈尔滨模拟)在△ABC中,∠ABC=45°,AB=2,AB边的垂直平分线交AB于D,交直线BC于点E,若CE=1,则线段DC的长为 1或 .
解:当E点在线段BC上时,
如图,过点D作DF⊥BC,垂足为F,
∵线段AB的垂直平分线交直线BC于点E,
∴AE=BE,
∴∠BAE=∠ABC=45°,
∴∠AEB=90°,
∵∠ABC=45°,∠BDE=90°,
∴∠BED=45°,
∴BD=ED,
∵AB=2,
∴BD=DE=,
∴BE==2,
∵BD=DE,DF⊥BE,
∴EF=BE=1,
∴DF=EF=1,
∵CE=1,
∴CF=2,
在Rt△CDF中,根据勾股定理得:
CD==;
当点E在BC的延长线上时,
如图,∵线段AB的垂直平分线交直线BC于点E,
∵∠ABC=45°,AB=2
,
由(1)同理可得:BE=2,
∵CE=1,
∴BC=1,
如图,过点C作CF⊥AB,垂足为F,
∴BF=CF==,
∴DF=,
在Rt△CDF中,由勾股定理得:
CD=,
综上:CD=1或,
(?http:?/??/?www.21cnjy.com?)
答案:1或.
(?http:?/??/?www.21cnjy.com?)
12.(2021?株洲模拟)如图,
(?http:?/??/?www.21cnjy.com?)已知直线m是正五边形ABCDE的对称轴,且直线m过点D,直线m与对角线BE相交于点O,则∠AOE= 72 度.【来源:21cnj
y.co
m】
(?http:?/??/?www.21cnjy.com?)
解:∵ABCDE是正五边形,
∴∠EAB=108°,
∵AE=AB,
∴∠AEB=∠ABE=36°,
∵直线m垂直平分线段AB,
∴OA=OB,
∴∠OAB=∠OBA=36°,
∴∠AOE=∠OAB+∠OBA=72°,
答案:72;
(?http:?/??/?www.21cnjy.com?)
13.(2021?枣庄模拟)如图,在矩形A
(?http:?/??/?www.21cnjy.com?)BCD中,AB=8,BC=4,一发光电子开始置于AB边的点P处,并设定此时为发光电子第一次与矩形的边碰撞,将发光电子沿着PR方向发射,碰撞到矩形的边时均反射,每次反射的反射角和入射角都等于45°,当发光电子与矩形的边碰撞2020次后,它与AB边的碰撞次数是 674 .
(?http:?/??/?www.21cnjy.com?)
解:如图以AB为x轴,AD为y轴,建立平面直角坐标系,
(?http:?/??/?www.21cnjy.com?)
根据图形可以得到:每6次反弹为一个循环组依次循环,经过6次反弹后动点回到出发点(6,0),且每次循环它与AB边的碰撞有2次,
∵2020÷6=336…4,
当点P第2020次碰到矩形的边时为第336个循环组的第4次反弹,点P的坐标为(2,0),
∴它与AB边的碰撞次数是=336×2+2=674(次),
答案:674.
14.(2021?沈阳模拟)如图,在△ABC中,∠A=45°,∠B=60°,AB=4,P是BC边上的动点(不与B,C重合),点P关于直线AB,AC的对称点分别为M,N,则线段MN长的取值范围是 2≤MN<4 .
(?http:?/??/?www.21cnjy.com?)
解:连接AM、AN、AP,如图所示.
∵点P关于直线AB,AC的对称点分别为M,N,
∴AM=AP=AN,∠MAB=∠PAB,∠NAC=∠PAC,
∴△MAN等腰直角三角形,
∴MN=AM=AP,
∴2≤AP<4,
∴2≤MN<4.
答案:2≤MN<4.
(?http:?/??/?www.21cnjy.com?)
15.(2021?西安模拟)如图,已知正方形ABCD的边长为5,l是过点A的任意一条直线,点M是点D关于直线l的对称点.连接CM,则线段CM长度的最大值是 5+5 .21cnjy.com
(?http:?/??/?www.21cnjy.com?)
解:如图,连接AC,AM.
(?http:?/??/?www.21cnjy.com?)
∵四边形ABCD是正方形,
∴∠D=90°,AD=CD=5,
∴AC=5,
∵D,M关于直线l对称,
∴AM=AD=5,
∵CM≤AC+AM=5+5,
∴CM的最大值为5+5.
16.(2021?延边模拟)如图
(?http:?/??/?www.21cnjy.com?),∠AOB=40°,点P在∠AOB的内部,点C,D分别是点P关于直线OA,OB的对称点,连接CD分别交OA,OB于点E、F.则∠EPF= 100° .
(?http:?/??/?www.21cnjy.com?)
解:如图,设OA交PC于R,OB交PD于T.
(?http:?/??/?www.21cnjy.com?)
∵点C、D分别是点P关于直线OA、OB的对称点,
∴OA垂直平分PC,OB垂直平分PD,
∴CE=PE,PF=DF,
∴∠PEF=2∠C,∠PFE=2∠D,
∵∠PRE=∠PTF=90°,
∴在四边形OTPR中,
∴∠CPD+∠AOB=180°,
∵∠EPF+2∠C+2∠D=180°,
即∠CPD+∠C+∠D=180°,
∴∠C+∠D=∠AOB=40°
∴∠EPF=180°﹣40°×2=100°.
答案:100°.
三、解答题
17.(2021?石家庄模拟)如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD,且交OE于点F.【出处:21教育名师】
(1)求证:OE是CD的垂直平分线.
(2)若∠AOB=60°,请你探究OE,EF之间有什么数量关系?并证明你的结论.
(?http:?/??/?www.21cnjy.com?)
解:(1)∵E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,
∴DE=CE,OE=OE,
∴Rt△ODE≌Rt△OCE,
∴OD=OC,
∴△DOC是等腰三角形,
∵OE是∠AOB的平分线,
∴OE是CD的垂直平分线;
(2)∵OE是∠AOB的平分线,∠AOB=60°,
∴∠AOE=∠BOE=30°,
∵EC⊥OB,ED⊥OA,
∴OE=2DE,∠ODF=∠OED=60°,
∴∠EDF=30°,
∴DE=2EF,
∴OE=4EF.
18.(2021?衡水模拟)如图,在△A
(?http:?/??/?www.21cnjy.com?)BC中,∠A=60°,点D是BC边的中点,DE⊥BC,∠ABC的角平分线BF交DE于△ABC内一点P,连接PC.www-2-1-cnjy-com
(1)若∠ACP=24°,求∠ABP的度数;
(2)若∠ACP=m°,∠ABP=n°,请直接写出m,n满足的关系式: m+3n=120 .
(?http:?/??/?www.21cnjy.com?)
解:(1)∵点D是BC边的中点,DE⊥BC,
∴PB=PC,
∴∠PBC=∠PCB,
∵BP平分∠ABC,
∴∠PBC=∠ABP,
∴∠PBC=∠PCB=∠ABP,
∵∠A=60°,∠ACP=24°,
∴∠PBC+∠PCB+∠ABP=120°﹣24°,
∴3∠ABP=120°﹣24°,
∴∠ABP=32°;
(2)∵点D是BC边的中点,DE⊥BC,
∴PB=PC,
∴∠PBC=∠PCB,
∵BP平分∠ABC,
∴∠PBC=∠ABP,
∴∠PBC=∠PCB=∠ABP=n°,
∵∠A=60°,∠ACP=m°,
∴∠PBC+∠PCB+∠ABP=120°﹣m°,
∴3∠ABP=120°﹣m°,
∴3n°+m°=120°,
答案:m+3n=120.
19.(2021?郑州模拟)如图,
(?http:?/??/?www.21cnjy.com?)在△ABC中,∠ABC=45°,点P为边BC上的一点,BC=3BP,且∠PAB=15°,点C关于直线PA的对称点为D,连接BD,又△APC的PC边上的高为AH21
cnjy
com
(1)求∠BPD的大小;
(2)判断直线BD,AH是否平行?并说明理由;
(3)证明:∠BAP=∠CAH.
(?http:?/??/?www.21cnjy.com?)
解:(1)∵∠PAB=15°,∠ABC=45°,
∴∠APC=15°+45°=60°,
∵点C关于直线PA的对称点为D,
∴PD=PC,AD=AC,
∴△ADP≌△ACP,
∴∠APC=∠APD=60°,
∴∠BPD=180°﹣120°=60°;
(2)直线BD,AH平行.理由:
∵BC=3BP,
∴BP=PC=PD,
如图,取PD中点E,连接BE,则△BEP为等边三角形,△BDE为等腰三角形,
(?http:?/??/?www.21cnjy.com?)
∴∠BEP=60°,
∴∠BDE=∠BEP=30°,
∴∠DBP=90°,即BD⊥BC.
又∵△APC的PC边上的高为AH,
∴AH⊥BC,
∴BD∥AH;
(3)如图,过点A作BD、DP的垂线,垂足分别为G、F.
(?http:?/??/?www.21cnjy.com?)
∵∠APC=∠APD,即点A在∠DPC的平分线上,
∴AH=AF.
∵∠CBD=90°,∠ABC=45°,
∴∠GBA=∠CBA=45°,
即点A在∠GBC的平分线上,
∴AG=AH,
∴AG=AF,
∴点A在∠GDP的平分线上.
又∵∠BDP=30°,
∴∠GDP=150°,
∴∠ADP=×150°=75°,
∴∠C=∠ADP=75°,
∴Rt△ACH中,∠CAH=15°,
∴∠BAP=∠CAH.
20.(2021?钦州模拟)如图,
(?http:?/??/?www.21cnjy.com?)在△ABC中,AB边的垂直平分线l1交BC于点D,AC边的垂直平分线l2交BC于点E,l1与l2相交于点O,连接OB,OC,若△ADE的周长为6cm,△OBC的周长为16cm.
(1)求线段BC的长;
(2)连接OA,求线段OA的长;
(3)若∠BAC=120°,求∠DAE的度数.
(?http:?/??/?www.21cnjy.com?)
解:(1)∵l1是AB边的垂直平分线
∴DA=DB,
∵l2是AC边的垂直平分线,
∴EA=EC,
BC=BD+DE+EC=DA+DE+EA=6cm;
(2)∵l1是AB边的垂直平分线,
∴OA=OB,
∵l2是AC边的垂直平分线,
∴OA=OC,
∵OB+OC+BC=16cm,
∴OA=0B=OC=5cm;
(3)∵∠BAC=120°,
∴∠ABC+∠ACB=60°,
∵DA=DB,EA=EC,
∴∠BAD=∠ABC,∠EAC=∠ACB,
∴∠DAE=∠BAC﹣∠BAD﹣∠EAC=60°.
(?http:?/??/?www.21cnjy.com?)
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
