5.2.3 由三种视图确定几何体 课件(共27张PPT)
文档属性
| 名称 | 5.2.3 由三种视图确定几何体 课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-19 09:09:29 | ||
图片预览






文档简介
(共27张PPT)
北师大版
九年级上
5.2
视图
第3课时
由三种视图确定几何体
学
习
目
标
1
2
能根据三视图想象出物体形状,进一步提高空间想象能力.
(难点)
由三视图想象出立体图形后能进行简单的面积或体积的计算.
(重点)
新课导入
A
C
B
D
问题:下面是哪个几何体的三视图?
主视图
左视图
俯视图
我们知道,由几何体可以画出三视图,反过来,能否由三视图还原几何体吗?
知识讲解
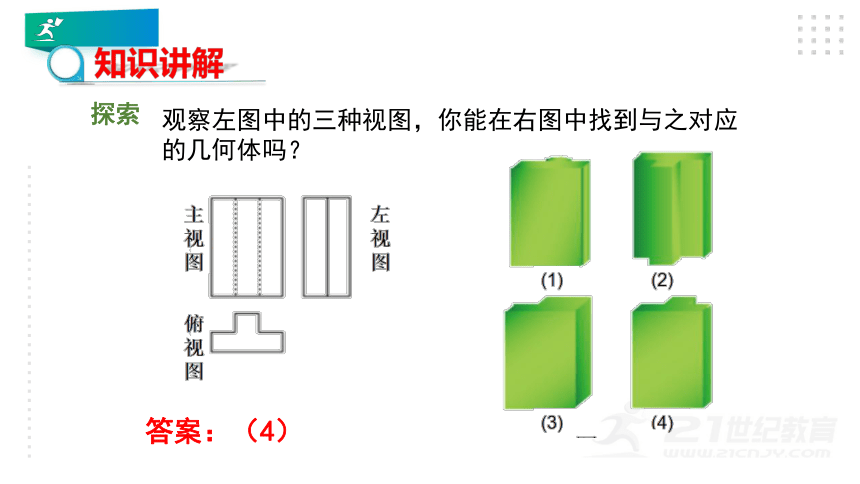
探索
观察左图中的三种视图,你能在右图中找到与之对应的几何体吗?
答案:(4)
根据图中的三种视图,你能想象出相应几何体的形状吗?先独立思考,再小组交流.
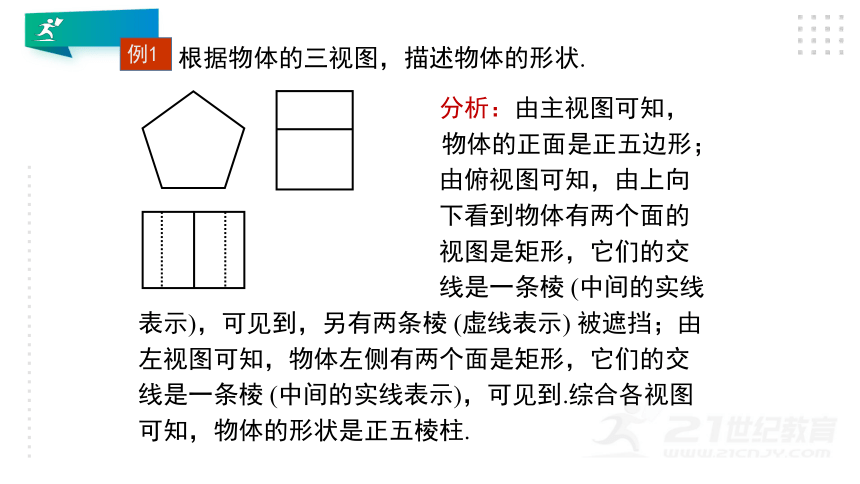
根据物体的三视图,描述物体的形状.
分析:由主视图可知,
物体的正面是正五边形;
由俯视图可知,由上向
下看到物体有两个面的
视图是矩形,它们的交
线是一条棱
(中间的实线表示),可见到,另有两条棱
(虚线表示)
被遮挡;由左视图可知,物体左侧有两个面是矩形,它们的交线是一条棱
(中间的实线表示),可见到.综合各视图可知,物体的形状是正五棱柱.
例1
解:物体是正五棱柱形状的,如图所示.
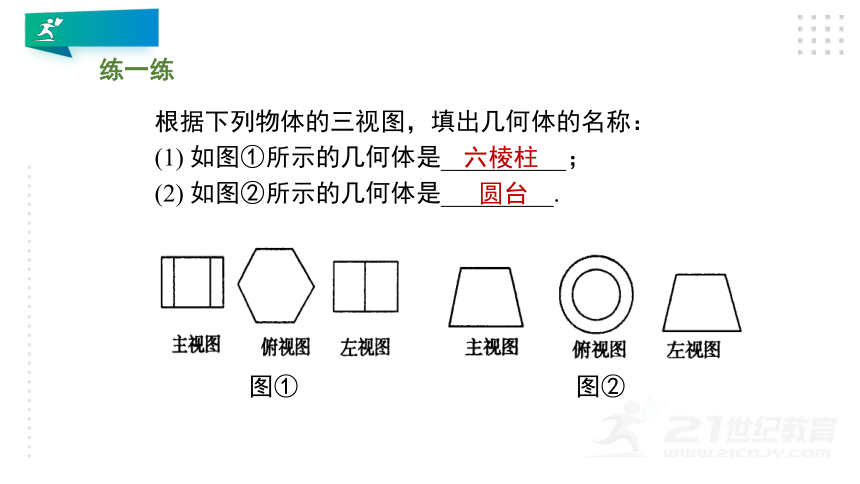
根据下列物体的三视图,填出几何体的名称:
(1)
如图①所示的几何体是__________;
(2)
如图②所示的几何体是_________.
图①
图②
六棱柱
圆台
练一练
由三视图想象立体图形时,先分别根据主视图、俯视图和左视图想象立体图形的前面、主面和左侧面的局部形状,然后再综合起来考虑整体图形.
归纳:
分析:
1.
应先由三视图想象出
;
2.
画出物体的
.
密封罐的形状
展开图
某工厂要加工一批密封罐,设计者给出了密封罐的三视图,请你按照三视图确定制作每个密封罐所需钢板的面积
(图中尺寸单位:mm).
例2
解:由三视图可知,密封罐的形状是正六棱柱.
50mm
50mm
密封罐的高为50mm,底面正六边形的直径为100mm,边长为50mm,
100mm
如图,是它的展开图.
由展开图可知,制作一个密封罐所需钢板的面积为
1.
三种图形的转化:
三种视图
立体图
展开图
2.
由三种视图求立体图形的面积的方法:
(1)
先根据给出的三种视图确定立体图形,并确定
立体图形的长、宽、高.
(2)
将立体图形展开成一个平面图形
(展开图),
观察它的组成部分.
(3)
最后根据已知数据,求出展开图的面积.
归纳:
练一练
一个机器零件的三视图如图所示(单位:cm),这个机器零件是一个什么样的立体图形?它的体积是多少?
15
10
12
15
10
主视图
左视图
俯视图
解:长方体,其体积为10×12×15=1800(cm3).
由几个相同的小立方块搭成的几何体的俯视图如图所示.方格中的数字表示该位置的小方块的个数.请画出这个几何体的主视图和左视图.
1
3
2
主视图
左视图
例3
1
3
2
主视图
1.由俯视图确定组合体的底部形状
左视图
2.根据俯视图上标注的小方块的个数及主视图和左视图,确定组合体的形状.
解:作法如下:
如何由三种视图确定小正方体的个数?
俯视图
根据三种视图确定小正方体的个数问题:
先由俯视图确定物体在平面上的形状,再根据主视图和左视图确定各行各列的高度.
较方便的做法是在俯视图的相应位置标出小正方形的个数,如:下图表示几何体共有4个小正方体组成.当只给出两种视图时,往往个数不确定.
1
2
1
归纳:
随堂训练
1.
一个几何体的三视图如图所示,则这个几何体是
(
)
A.四棱锥
B.四棱柱
C.三棱锥
D.三棱柱
D
2.
一个长方体的左视图、俯视图及相关数据如图所示,
则其主视图的面积为
(
)
A.
6
B.
8
C.
12
D.
24
B
3.
一个物体的俯视图是圆,则该物体有可能是
.
圆柱、球
4.
在一仓库里堆放着若干相同的正方体货箱,仓库管
理员将这堆货箱的三视图画了出来.
如下图所示,
则这堆正方体货箱共有
箱.
9
5.
如图是一个由若干个棱长为1cm的正方体构成的几何
体的三视图.
(1)
请写出构成这个几何体的正方体的个数为
;
(2)
计算这个几何体的表面积为
.
5
20cm2
6.
(1)
一个几何体的主视图和左视图如图所示,请补画
这个几何体的俯视图.
(2)
一个直棱柱的主视图和俯视图如图所示.
描述这
个直棱柱的形状,并补画它的左视图.
左视图
主视图
俯视图
主视图
俯视图
左视图
7.
如图是一个几何体的三视图,试描绘出这个零件的
形状,并求出此三视图所描述的几何体的表面积.
解:该几何体的表面积为
π×22+2π×2×2+1/2×4×4π=20
π.
课堂小结
由三视图确定几何体
由三视图确定简单几何体
由三视图确定复杂几何体
由三视图确定简单几何体的组合体
https://www.21cnjy.com/help/help_extract.php
北师大版
九年级上
5.2
视图
第3课时
由三种视图确定几何体
学
习
目
标
1
2
能根据三视图想象出物体形状,进一步提高空间想象能力.
(难点)
由三视图想象出立体图形后能进行简单的面积或体积的计算.
(重点)
新课导入
A
C
B
D
问题:下面是哪个几何体的三视图?
主视图
左视图
俯视图
我们知道,由几何体可以画出三视图,反过来,能否由三视图还原几何体吗?
知识讲解
探索
观察左图中的三种视图,你能在右图中找到与之对应的几何体吗?
答案:(4)
根据图中的三种视图,你能想象出相应几何体的形状吗?先独立思考,再小组交流.
根据物体的三视图,描述物体的形状.
分析:由主视图可知,
物体的正面是正五边形;
由俯视图可知,由上向
下看到物体有两个面的
视图是矩形,它们的交
线是一条棱
(中间的实线表示),可见到,另有两条棱
(虚线表示)
被遮挡;由左视图可知,物体左侧有两个面是矩形,它们的交线是一条棱
(中间的实线表示),可见到.综合各视图可知,物体的形状是正五棱柱.
例1
解:物体是正五棱柱形状的,如图所示.
根据下列物体的三视图,填出几何体的名称:
(1)
如图①所示的几何体是__________;
(2)
如图②所示的几何体是_________.
图①
图②
六棱柱
圆台
练一练
由三视图想象立体图形时,先分别根据主视图、俯视图和左视图想象立体图形的前面、主面和左侧面的局部形状,然后再综合起来考虑整体图形.
归纳:
分析:
1.
应先由三视图想象出
;
2.
画出物体的
.
密封罐的形状
展开图
某工厂要加工一批密封罐,设计者给出了密封罐的三视图,请你按照三视图确定制作每个密封罐所需钢板的面积
(图中尺寸单位:mm).
例2
解:由三视图可知,密封罐的形状是正六棱柱.
50mm
50mm
密封罐的高为50mm,底面正六边形的直径为100mm,边长为50mm,
100mm
如图,是它的展开图.
由展开图可知,制作一个密封罐所需钢板的面积为
1.
三种图形的转化:
三种视图
立体图
展开图
2.
由三种视图求立体图形的面积的方法:
(1)
先根据给出的三种视图确定立体图形,并确定
立体图形的长、宽、高.
(2)
将立体图形展开成一个平面图形
(展开图),
观察它的组成部分.
(3)
最后根据已知数据,求出展开图的面积.
归纳:
练一练
一个机器零件的三视图如图所示(单位:cm),这个机器零件是一个什么样的立体图形?它的体积是多少?
15
10
12
15
10
主视图
左视图
俯视图
解:长方体,其体积为10×12×15=1800(cm3).
由几个相同的小立方块搭成的几何体的俯视图如图所示.方格中的数字表示该位置的小方块的个数.请画出这个几何体的主视图和左视图.
1
3
2
主视图
左视图
例3
1
3
2
主视图
1.由俯视图确定组合体的底部形状
左视图
2.根据俯视图上标注的小方块的个数及主视图和左视图,确定组合体的形状.
解:作法如下:
如何由三种视图确定小正方体的个数?
俯视图
根据三种视图确定小正方体的个数问题:
先由俯视图确定物体在平面上的形状,再根据主视图和左视图确定各行各列的高度.
较方便的做法是在俯视图的相应位置标出小正方形的个数,如:下图表示几何体共有4个小正方体组成.当只给出两种视图时,往往个数不确定.
1
2
1
归纳:
随堂训练
1.
一个几何体的三视图如图所示,则这个几何体是
(
)
A.四棱锥
B.四棱柱
C.三棱锥
D.三棱柱
D
2.
一个长方体的左视图、俯视图及相关数据如图所示,
则其主视图的面积为
(
)
A.
6
B.
8
C.
12
D.
24
B
3.
一个物体的俯视图是圆,则该物体有可能是
.
圆柱、球
4.
在一仓库里堆放着若干相同的正方体货箱,仓库管
理员将这堆货箱的三视图画了出来.
如下图所示,
则这堆正方体货箱共有
箱.
9
5.
如图是一个由若干个棱长为1cm的正方体构成的几何
体的三视图.
(1)
请写出构成这个几何体的正方体的个数为
;
(2)
计算这个几何体的表面积为
.
5
20cm2
6.
(1)
一个几何体的主视图和左视图如图所示,请补画
这个几何体的俯视图.
(2)
一个直棱柱的主视图和俯视图如图所示.
描述这
个直棱柱的形状,并补画它的左视图.
左视图
主视图
俯视图
主视图
俯视图
左视图
7.
如图是一个几何体的三视图,试描绘出这个零件的
形状,并求出此三视图所描述的几何体的表面积.
解:该几何体的表面积为
π×22+2π×2×2+1/2×4×4π=20
π.
课堂小结
由三视图确定几何体
由三视图确定简单几何体
由三视图确定复杂几何体
由三视图确定简单几何体的组合体
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
