6.1 反比例函数 课件(共17张PPT)
文档属性
| 名称 | 6.1 反比例函数 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-19 09:19:12 | ||
图片预览






文档简介
(共17张PPT)
北师大版
九年级上
第六章
反比例函数
6.1
反比例函数
学
习
目
标
3
1
2
理解反比例函数的概念.
能根据实际问题中的条件确定反比例函数的解析式.
能判断一个函数是否为反比例函数.
1.
函数的定义
一般地,在一个变化的过程中,如果有两个变量x与y,并且对于x的每一
个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是x的
函数.
一般地,形如(是常数,)的函数叫做一次函数.当时,一次函数就叫做正比例函数.
2.
一次函数与正比例函数
温故知新
下列问题中,变量间的对应关系可以用怎样的函数关系表示?这些函数有什么共同特点?
新课导入
1.京沪铁路全程为,某次列车的平均速度(单位:km/h)随此次列车的全程运行时间(单位:h)的变化而变化.
2.某住宅小区要种植一块面积为m2的矩形草坪,草坪的长(单位:m)随宽
(单位:m)的变化而变化.
或
3.已知北京市的总面积为,人均占有面积(单位:
/人)随全市总人口(单位:人)的变化而变化.
知识讲解
1.由上面的问题我们得到这样的三个函数
2.上面的函数解析式形式上有什么的共同点?
都具有的形式,其中是非零常数
1.反比例函数的定义
反比例函数的定义
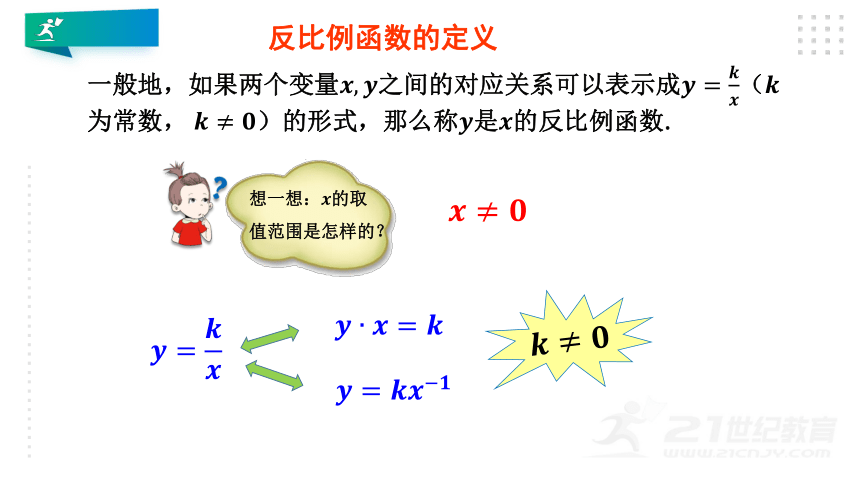
一般地,如果两个变量之间的对应关系可以表示成(为常数,
)的形式,那么称是的反比例函数.
想一想:的取值范围是怎样的?
练一练:下列函数中哪些是反比例函数?哪些是一次函数?
反比例函数
一次函数
已知是的反比例函数,并且当时,.
(1)写出的函数解析式;
(2)当4时,求的值.
待定系数法
例1
2.确定反比例函数的解析式
(1)设.因为当时,,所以有
解:
.
解得
因此
(2)
把代入,得
是的反比例函数,下表给出了与的一些值.
例2
请完成上表并写出这个反比例函数的解析式.
4
∵
是的反比例函数,
解:
∴设.
把代入上式得,
,
∴
∴
练一练
已知与成反比例,当时,.
写出与的函数解析式;
求当时的值.
(1)设,因为当时,所以
解:
4,
解得
因此与的函数解析式为
(2)
把代入,得
用函数解析式表示下列问题中变量间的对应关系:
平行四边形的面积是35,它的一边长随这边上的高的变化而变化;
某小区绿地总面积是400
,该小区的人均绿地面积数随人口数的变化而变化.
解:
(1);
(2).
例3
3.实际问题中的反比例函数
随堂训练
2.
若反比例函数的图象经过点,则的值为(
)
A.-6
B.6
C.-5
D.5
C
3.下列各点中,在函数
的图象上的是(
)
A.(-2,-4)
B.(2,3)
C.(-6,1)
D.(-
,3)
.
1.若函数是反比例函数,则的值为(
)
A.-1
B.1
C.2或-2
D.-1或1
B
4.已知都在的图象上,若,求的值.
解:
又∵
∴
课堂小结
反比例函数
定
义
,
常见其他形式
如果两个变量之间的对应关系可以表示成(为常数,
)的形式
待定系数法确定函数解析式
确定一对的值或者图象上一个点的坐标,代入确定的值
https://www.21cnjy.com/help/help_extract.php
北师大版
九年级上
第六章
反比例函数
6.1
反比例函数
学
习
目
标
3
1
2
理解反比例函数的概念.
能根据实际问题中的条件确定反比例函数的解析式.
能判断一个函数是否为反比例函数.
1.
函数的定义
一般地,在一个变化的过程中,如果有两个变量x与y,并且对于x的每一
个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是x的
函数.
一般地,形如(是常数,)的函数叫做一次函数.当时,一次函数就叫做正比例函数.
2.
一次函数与正比例函数
温故知新
下列问题中,变量间的对应关系可以用怎样的函数关系表示?这些函数有什么共同特点?
新课导入
1.京沪铁路全程为,某次列车的平均速度(单位:km/h)随此次列车的全程运行时间(单位:h)的变化而变化.
2.某住宅小区要种植一块面积为m2的矩形草坪,草坪的长(单位:m)随宽
(单位:m)的变化而变化.
或
3.已知北京市的总面积为,人均占有面积(单位:
/人)随全市总人口(单位:人)的变化而变化.
知识讲解
1.由上面的问题我们得到这样的三个函数
2.上面的函数解析式形式上有什么的共同点?
都具有的形式,其中是非零常数
1.反比例函数的定义
反比例函数的定义
一般地,如果两个变量之间的对应关系可以表示成(为常数,
)的形式,那么称是的反比例函数.
想一想:的取值范围是怎样的?
练一练:下列函数中哪些是反比例函数?哪些是一次函数?
反比例函数
一次函数
已知是的反比例函数,并且当时,.
(1)写出的函数解析式;
(2)当4时,求的值.
待定系数法
例1
2.确定反比例函数的解析式
(1)设.因为当时,,所以有
解:
.
解得
因此
(2)
把代入,得
是的反比例函数,下表给出了与的一些值.
例2
请完成上表并写出这个反比例函数的解析式.
4
∵
是的反比例函数,
解:
∴设.
把代入上式得,
,
∴
∴
练一练
已知与成反比例,当时,.
写出与的函数解析式;
求当时的值.
(1)设,因为当时,所以
解:
4,
解得
因此与的函数解析式为
(2)
把代入,得
用函数解析式表示下列问题中变量间的对应关系:
平行四边形的面积是35,它的一边长随这边上的高的变化而变化;
某小区绿地总面积是400
,该小区的人均绿地面积数随人口数的变化而变化.
解:
(1);
(2).
例3
3.实际问题中的反比例函数
随堂训练
2.
若反比例函数的图象经过点,则的值为(
)
A.-6
B.6
C.-5
D.5
C
3.下列各点中,在函数
的图象上的是(
)
A.(-2,-4)
B.(2,3)
C.(-6,1)
D.(-
,3)
.
1.若函数是反比例函数,则的值为(
)
A.-1
B.1
C.2或-2
D.-1或1
B
4.已知都在的图象上,若,求的值.
解:
又∵
∴
课堂小结
反比例函数
定
义
,
常见其他形式
如果两个变量之间的对应关系可以表示成(为常数,
)的形式
待定系数法确定函数解析式
确定一对的值或者图象上一个点的坐标,代入确定的值
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
