6.2.1 反比例函数的图象与性质 课件(共17张PPT)
文档属性
| 名称 | 6.2.1 反比例函数的图象与性质 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-19 09:20:09 | ||
图片预览




文档简介
北师大版 九年级上
第六章 反比例函数
6.2 反比例函数的图象和性质
(第1课时)
学 习 目 标
1
2
学会用描点法作反比例函数的图象,能结合函数图象进行探索.
理解并掌握反比例函数的性质,会应用反比例函数的性质解决问题.
温故知新
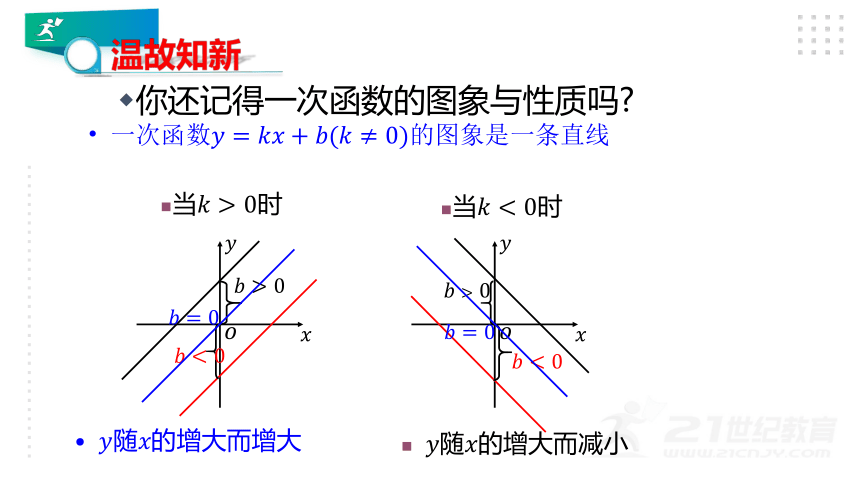
你还记得一次函数的图象与性质吗?
一次函数????=????????+????(????≠0)的图象是一条直线
?
????随????的增大而增大
?
????
?
????
?
????
?
????
?
????
?
????
?
????随????的增大而减小
?
????<0
?
????>0
?
????=0
?
????<0
?
????>0
?
????=0
?
当????>0时
?
当????<0时
?
你还记得作函数图象的一般步骤吗?
反比例函数的概念?
用图象法表示函数关系时,首先在自变量的取值范围内取一些值,列表,描点,连线(按自变量从小到大的顺序,用一条平滑的曲线连接起来).
一般地,如果两个变量????,????之间的关系可以表示成????=????????(????为常数,????≠0)的形式,那么称????是????的反比例函数.
?
知识讲解
反比例函数的图象和性质
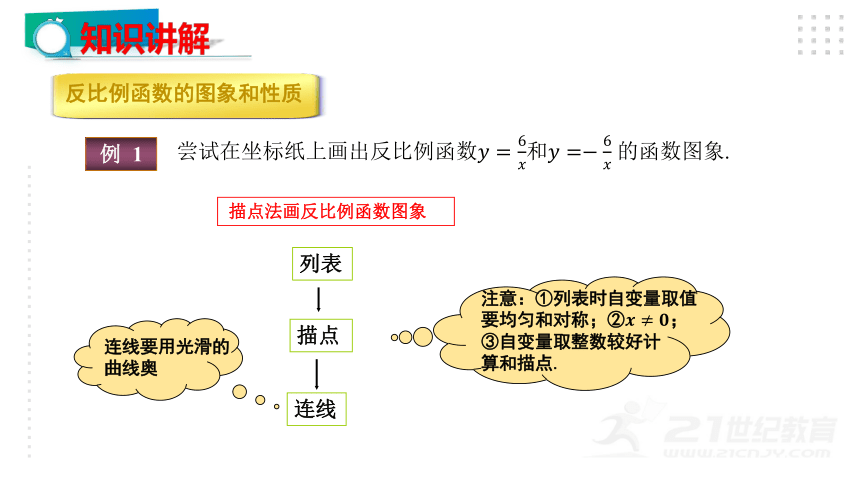
尝试在坐标纸上画出反比例函数????=6????和????=?6???? 的函数图象.
?
例 1
列表
描点
连线
描点法画反比例函数图象
注意:①列表时自变量取值
要均匀和对称;②????≠????;
③自变量取整数较好计
算和描点.
?
连线要用光滑的
曲线奥
????
????=6????
????=?6????
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
O
-6
-5
5
6
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????.????
?
????
?
????.????
?
????
?
????
?
?????
?
?????
?
?????
?
?????
?
?????
?
?????.????
?
?????
?
?????
?
?????
?
?????.????
?
?????
?
?????
?
…
…
…
…
?????
?
????
?
????
?
?????
?
????
?
?????
?
????.????
?
?????.????
?
????.????
?
?????.????
?
????
?
?????
?
…
…
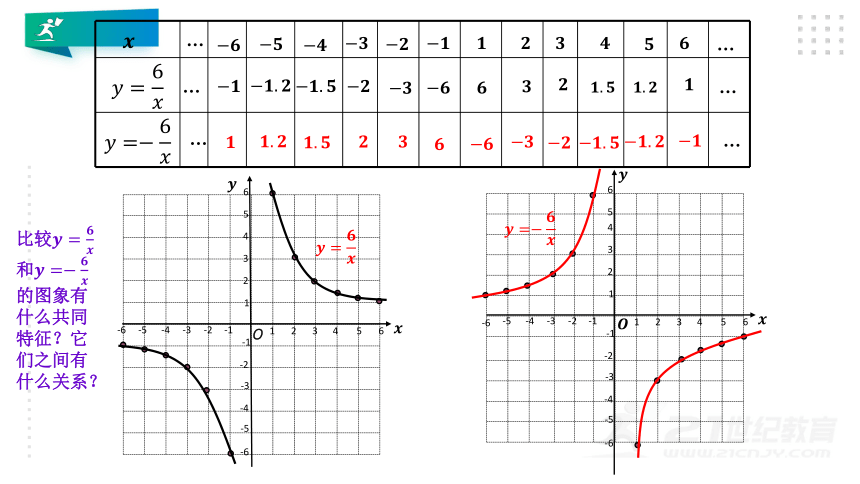
比较????=???????? 和????=????????? 的图象有什么共同特征?它们之间有什么关系?
?
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
????
?
-6
-5
5
6
????
?
????
?
????=????????
?
????=?????????
?
1.列表时,自变量的值可以选取一些互为相反数的值这样既可简化计算,又便于对称性描点;
2.列表描点时,要尽量多取一些数值,多描一些点,这样既可以方便连线,又较准确地表达函数的变化趋势;
3.连线时,一定要养成按自变量从小到大的顺序,
依次用平滑的曲线连接,从中体会函数的增减性;
……
????=????
?
????=?????
?
?????=????????
?
?????=?????????
?
反比例函数的图象既是轴对称图形又是中心对称图形.
有两条对称轴:直线????=????和 ????=?????.
对称中心是:原点
?
思考:反比例函数的图象和性质
反比例函数的图象是由两支双曲线组成的.
因此称反比例函数的图象为双曲线.
当????>0时,两支双曲线分位于第一、三象限内;
当????<0时,两支双曲线分别位于第二、四象限内.
?
1.这几个函数图象有什么共同点?
2.函数图象分别位于哪几个象限?
想一想: ????值随????值的变化有怎样的变化?
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
?????=????????
?
图象
性质
????>????
?
?????
归纳
????
?
????
?
????
?
????
?
????
?
????
?
函数图象的两个分支分别在第一、三象限,在每个象限内,????随????的增大而减小
?
函数图象的两个分支分别在第二、四象限,在每个象限内,????随????的增大而增大
?
已知????????,????????,(????????,????????),(????????,????????)是反比例函数????=?????????的图象上的三个点,且????????<????????<????,????????>????,则????????,????????,????????的大小关系是( )
????.????????<????????<???????? ????.????????<????????<????????
????.????????<????????<???????????????????????????????????????????.????????<????????<????????
?
例 2
解析:
反比例函数????=?????????的图象在二、四象限,
?
在第二象限????随????的增大而增大,且????>????,
?
????
?
????
?
????
?
????=?????????
?
在第四象限????<????,所以????????<????.
?
所以????????<????????.
?
A
????????<????????<????????
?
已知反比例函数????=2????+4????的图象在第一、三象限,反比例函数????=?????3????在????>0时,????随????的增大而增大,则????的取值范围是_______.
【解析】∵ ????=2????+4????的图象在第一、三象限,
∴????????+????>????.
由于????=?????3????在????>????时,????随????的增大而增大,∴?????????<0.
综上,????需满足????????+????>????,?????????<0,
解得:?????<????<????.
【答案】?????<????<????
?
练一练
1、函数????=20????的图象在第________象限,在每一象限内,????随????的增大而_________.
2、 函数????=?5????的图象在第________象限,在每一象限内,????随???? 的增大而_________.
3、函数????=52???? ,当????>0时,图象在第____象限,????随?????的增大而_________.
?
随堂训练
一、三
二、四
一
减小
增大
减小
4. 已知函数????=(????+????)?????????????????是反比例函数,且图象在第二、四象限内,则????的值是( )
A.2 B.-2 C.±2 D.?????????
?
B
课堂小结
反比例函数
反比例函数的图象和性质
形状 反比例函数的图象是由两支双曲线组成的.因此称反比例函数的图象为双曲线;
位置 当????>0时,两支双曲线分别位于第一,三象限内; 当????<0时,两支双曲线分别位于第二,四象限内.
?
一般地,如果两个变量????,????之间的关系可以表示成????=????????(????为常数,????≠0)的形式,那么称????是????的反比例函数.
?
https://www.21cnjy.com/help/help_extract.php
第六章 反比例函数
6.2 反比例函数的图象和性质
(第1课时)
学 习 目 标
1
2
学会用描点法作反比例函数的图象,能结合函数图象进行探索.
理解并掌握反比例函数的性质,会应用反比例函数的性质解决问题.
温故知新
你还记得一次函数的图象与性质吗?
一次函数????=????????+????(????≠0)的图象是一条直线
?
????随????的增大而增大
?
????
?
????
?
????
?
????
?
????
?
????
?
????随????的增大而减小
?
????<0
?
????>0
?
????=0
?
????<0
?
????>0
?
????=0
?
当????>0时
?
当????<0时
?
你还记得作函数图象的一般步骤吗?
反比例函数的概念?
用图象法表示函数关系时,首先在自变量的取值范围内取一些值,列表,描点,连线(按自变量从小到大的顺序,用一条平滑的曲线连接起来).
一般地,如果两个变量????,????之间的关系可以表示成????=????????(????为常数,????≠0)的形式,那么称????是????的反比例函数.
?
知识讲解
反比例函数的图象和性质
尝试在坐标纸上画出反比例函数????=6????和????=?6???? 的函数图象.
?
例 1
列表
描点
连线
描点法画反比例函数图象
注意:①列表时自变量取值
要均匀和对称;②????≠????;
③自变量取整数较好计
算和描点.
?
连线要用光滑的
曲线奥
????
????=6????
????=?6????
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
O
-6
-5
5
6
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????.????
?
????
?
????.????
?
????
?
????
?
?????
?
?????
?
?????
?
?????
?
?????
?
?????.????
?
?????
?
?????
?
?????
?
?????.????
?
?????
?
?????
?
…
…
…
…
?????
?
????
?
????
?
?????
?
????
?
?????
?
????.????
?
?????.????
?
????.????
?
?????.????
?
????
?
?????
?
…
…
比较????=???????? 和????=????????? 的图象有什么共同特征?它们之间有什么关系?
?
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
????
?
-6
-5
5
6
????
?
????
?
????=????????
?
????=?????????
?
1.列表时,自变量的值可以选取一些互为相反数的值这样既可简化计算,又便于对称性描点;
2.列表描点时,要尽量多取一些数值,多描一些点,这样既可以方便连线,又较准确地表达函数的变化趋势;
3.连线时,一定要养成按自变量从小到大的顺序,
依次用平滑的曲线连接,从中体会函数的增减性;
……
????=????
?
????=?????
?
?????=????????
?
?????=?????????
?
反比例函数的图象既是轴对称图形又是中心对称图形.
有两条对称轴:直线????=????和 ????=?????.
对称中心是:原点
?
思考:反比例函数的图象和性质
反比例函数的图象是由两支双曲线组成的.
因此称反比例函数的图象为双曲线.
当????>0时,两支双曲线分位于第一、三象限内;
当????<0时,两支双曲线分别位于第二、四象限内.
?
1.这几个函数图象有什么共同点?
2.函数图象分别位于哪几个象限?
想一想: ????值随????值的变化有怎样的变化?
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
?????=????????
?
图象
性质
????>????
?
?????
归纳
????
?
????
?
????
?
????
?
????
?
????
?
函数图象的两个分支分别在第一、三象限,在每个象限内,????随????的增大而减小
?
函数图象的两个分支分别在第二、四象限,在每个象限内,????随????的增大而增大
?
已知????????,????????,(????????,????????),(????????,????????)是反比例函数????=?????????的图象上的三个点,且????????<????????<????,????????>????,则????????,????????,????????的大小关系是( )
????.????????<????????<???????? ????.????????<????????<????????
????.????????<????????<???????????????????????????????????????????.????????<????????<????????
?
例 2
解析:
反比例函数????=?????????的图象在二、四象限,
?
在第二象限????随????的增大而增大,且????>????,
?
????
?
????
?
????
?
????=?????????
?
在第四象限????<????,所以????????<????.
?
所以????????<????????.
?
A
????????<????????<????????
?
已知反比例函数????=2????+4????的图象在第一、三象限,反比例函数????=?????3????在????>0时,????随????的增大而增大,则????的取值范围是_______.
【解析】∵ ????=2????+4????的图象在第一、三象限,
∴????????+????>????.
由于????=?????3????在????>????时,????随????的增大而增大,∴?????????<0.
综上,????需满足????????+????>????,?????????<0,
解得:?????<????<????.
【答案】?????<????<????
?
练一练
1、函数????=20????的图象在第________象限,在每一象限内,????随????的增大而_________.
2、 函数????=?5????的图象在第________象限,在每一象限内,????随???? 的增大而_________.
3、函数????=52???? ,当????>0时,图象在第____象限,????随?????的增大而_________.
?
随堂训练
一、三
二、四
一
减小
增大
减小
4. 已知函数????=(????+????)?????????????????是反比例函数,且图象在第二、四象限内,则????的值是( )
A.2 B.-2 C.±2 D.?????????
?
B
课堂小结
反比例函数
反比例函数的图象和性质
形状 反比例函数的图象是由两支双曲线组成的.因此称反比例函数的图象为双曲线;
位置 当????>0时,两支双曲线分别位于第一,三象限内; 当????<0时,两支双曲线分别位于第二,四象限内.
?
一般地,如果两个变量????,????之间的关系可以表示成????=????????(????为常数,????≠0)的形式,那么称????是????的反比例函数.
?
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
