6.2.2 反比例函数的图象与性质 课件(共22张PPT)
文档属性
| 名称 | 6.2.2 反比例函数的图象与性质 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-19 09:21:09 | ||
图片预览







文档简介
(共22张PPT)
北师大版
九年级上
第六章
反比例函数
6.
2
反比例函数的图象与性质
(第2课时)
学
习
目
标
1
2
进一步理解和掌握反比例函数的图象及性质,能灵活运用函数图象和性质解决一些较综合的问题.
理解反比例函数的几何意义,并会应用其解决问题.
温故知新
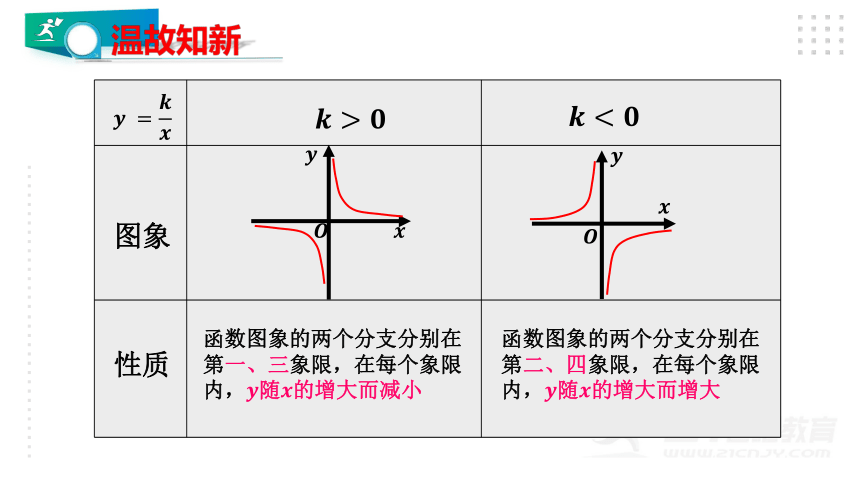
图象
性质
函数图象的两个分支分别在第一、三象限,在每个象限内,随的增大而减小
函数图象的两个分支分别在第二、四象限,在每个象限内,随的增大而增大
知识讲解
1.反比例函数的图象和性质的应用
已知反比例函数的图象经过点.
(1)这个函数的图象位于哪些象限?随的增大如何变化?
(2)点,,是否在这个函数的图象上?
例
1
解
在每个象限内,随的增大而减小.
(1)因为在第一象限,
所以这个函数的图象位于第一、第三象限,
(2)设这个反比例函数的解析式为,
因为点在其图象上,所以点的坐标满足,
即解得.
所以,这个反比例函数的解析式为.
因为点的坐标都满足点的坐标不满足,
所以点在函数的图象上,点不在这个函数的图象上.
如图,已知反比例函数与一次函数的图象在第一象限相交于点.
(1)试确定这两个函数的解析式;
(2)求出这两个函数图象的另一个交点的坐标,并
根据图象写出反比例函数的值大于一次函数的值的的取值范围.
例
2
【解】
(1)把点坐标代入反比例函数解析式,得,
∴这两个函数的解析式为和.
解得,
把代入,得
待定系数法确定函数解析式
(2)由方程组
由图象得反比例函数的值大于一次函数的值的的取值范围是:.
交点的坐标满足这个方程组
解得
∴点的坐标为(-2,-1).
练一练
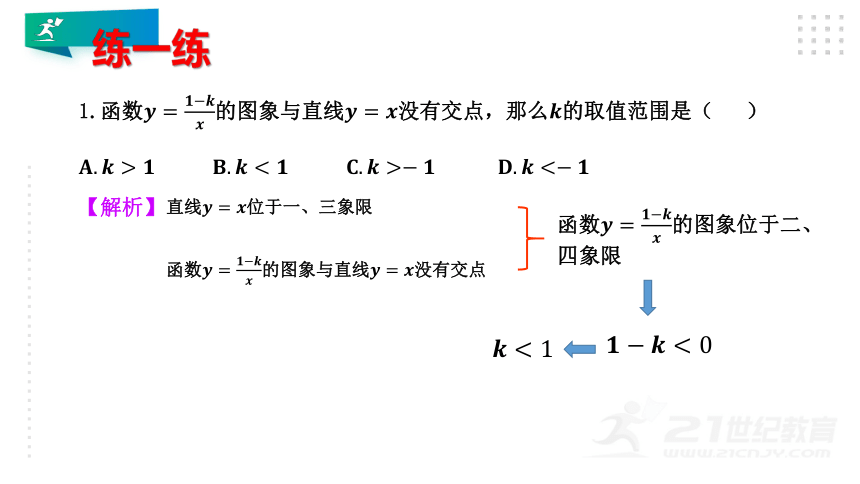
1.函数的图象与直线没有交点,那么的取值范围是(
)
直线位于一、三象限
【解析】
函数的图象与直线没有交点
函数的图象位于二、四象限
2.如图,一次函数的图象与反比例函数的图象交于点
,,交轴于点,交轴于点.
(1)求反比例函数和一次函数的解析式;
(2)连接求的面积.
(1)∵反比例函数的图象过点,
∴.
∴
反比例函数的解析式为.
∵
点在反比例函数的图象上,
∴
∴的坐标为.
【解】
∵一次函数的图象经过点,将这两个点的坐标代入,得
解得
∴所求一次函数的解析式为.
(2)∵一次函数的图象交轴于点,
∴
点坐标为,
∴
.
∵点的横坐标为-2,点的横坐标为5,
∴
.
面积分割
1的值
2的值
1与2的关系
猜想与k的关系
(2,2)
(4,1)
探究交流
1.在反比例函数
的图象上分别取点向x轴、y轴作垂线,围成面积分别为1,2的矩形,填写表格:
4
4
1
2
3
4
5
-1
-3
-2
-4
-5
1
2
3
4
-1
-2
-3
-4
-5
5
x
y
O
1
2
2.反比例函数比例系数的几何意义
1的值
的值
与的关系
猜想与的关系
2.若在反比例函数
中也用同样的方法分别取两点,填写表格:
4
4
y
x
o
P
Q
S1
S2
总结
过双曲线
任意一点
分别作
轴、
轴的垂线
,连接
.
∵∴
∴
.
如图,矩形的面积为4,反比例函数的图象的一支经过矩形对角线的交点,则该反比例函数的解析式是(
)
A.B.
C.
D.
例
3
解析:
C
过点作⊥,
由反比例函数的几何意义可知,△
,
又因为反比例函数图象在第一象限,所以,
由矩形的性质可知△
即
,
解得.
所以,所以
根据图中点的坐标:
(1)求出与的函数解析式;
(2)如果点在双曲线上,求的值.
(3)比较绿色部分和黄色部分的面积的大小.
(3)绿色部分和黄色部分的面积相等,都等于︱︱
答案:(1)
(2)
练一练
随堂训练
1.已知反比例函数下列结论不正确的是(
)
A.图象经过点(1,1)
B.图象在第一、三象限
C.当时,
D.当时,随着的增大而增大
C
2.如图,是反比例函数的图象上的一点,
⊥轴于点,且的面积是3,则的
值是(
)
A.3
B.-3
C.6
D.-6
C
3.函数的图象如图所示,下列结论:
(1)两函数图象的交点坐标为;
(2)当时,;
(3)直线分别与两函数图象交于点两点,则线段的长为3;
(4)当逐渐增大时,的值随着的增大而增大,的值随着的增大而减小.
则其中正确的是(
)
A.只有(1)(2)
B.只有(1)(3)
C.只有(2)(4)
D.只有(1)(3)(4)
D
解:点关于轴的对称点是
∵
点在一次函数的图象上,
∴
∵
点在反比例函数的图象上,∴.
∴
反比例函数的解析式.
课堂小结
反比例函数的图象和性质
形状
反比例函数的图象是由两支双曲线组成的.因此称反比例函数的图象为双曲线;
位置
当时,两支双曲线分别位于第一,三象限内;
当时,两支双曲线分别位于第二,四象限内.
反比例函数比例系数的几何意义
过双曲线
任意一点
分别作
轴、
轴的垂线
,连接
.
则
.
https://www.21cnjy.com/help/help_extract.php
北师大版
九年级上
第六章
反比例函数
6.
2
反比例函数的图象与性质
(第2课时)
学
习
目
标
1
2
进一步理解和掌握反比例函数的图象及性质,能灵活运用函数图象和性质解决一些较综合的问题.
理解反比例函数的几何意义,并会应用其解决问题.
温故知新
图象
性质
函数图象的两个分支分别在第一、三象限,在每个象限内,随的增大而减小
函数图象的两个分支分别在第二、四象限,在每个象限内,随的增大而增大
知识讲解
1.反比例函数的图象和性质的应用
已知反比例函数的图象经过点.
(1)这个函数的图象位于哪些象限?随的增大如何变化?
(2)点,,是否在这个函数的图象上?
例
1
解
在每个象限内,随的增大而减小.
(1)因为在第一象限,
所以这个函数的图象位于第一、第三象限,
(2)设这个反比例函数的解析式为,
因为点在其图象上,所以点的坐标满足,
即解得.
所以,这个反比例函数的解析式为.
因为点的坐标都满足点的坐标不满足,
所以点在函数的图象上,点不在这个函数的图象上.
如图,已知反比例函数与一次函数的图象在第一象限相交于点.
(1)试确定这两个函数的解析式;
(2)求出这两个函数图象的另一个交点的坐标,并
根据图象写出反比例函数的值大于一次函数的值的的取值范围.
例
2
【解】
(1)把点坐标代入反比例函数解析式,得,
∴这两个函数的解析式为和.
解得,
把代入,得
待定系数法确定函数解析式
(2)由方程组
由图象得反比例函数的值大于一次函数的值的的取值范围是:.
交点的坐标满足这个方程组
解得
∴点的坐标为(-2,-1).
练一练
1.函数的图象与直线没有交点,那么的取值范围是(
)
直线位于一、三象限
【解析】
函数的图象与直线没有交点
函数的图象位于二、四象限
2.如图,一次函数的图象与反比例函数的图象交于点
,,交轴于点,交轴于点.
(1)求反比例函数和一次函数的解析式;
(2)连接求的面积.
(1)∵反比例函数的图象过点,
∴.
∴
反比例函数的解析式为.
∵
点在反比例函数的图象上,
∴
∴的坐标为.
【解】
∵一次函数的图象经过点,将这两个点的坐标代入,得
解得
∴所求一次函数的解析式为.
(2)∵一次函数的图象交轴于点,
∴
点坐标为,
∴
.
∵点的横坐标为-2,点的横坐标为5,
∴
.
面积分割
1的值
2的值
1与2的关系
猜想与k的关系
(2,2)
(4,1)
探究交流
1.在反比例函数
的图象上分别取点向x轴、y轴作垂线,围成面积分别为1,2的矩形,填写表格:
4
4
1
2
3
4
5
-1
-3
-2
-4
-5
1
2
3
4
-1
-2
-3
-4
-5
5
x
y
O
1
2
2.反比例函数比例系数的几何意义
1的值
的值
与的关系
猜想与的关系
2.若在反比例函数
中也用同样的方法分别取两点,填写表格:
4
4
y
x
o
P
Q
S1
S2
总结
过双曲线
任意一点
分别作
轴、
轴的垂线
,连接
.
∵∴
∴
.
如图,矩形的面积为4,反比例函数的图象的一支经过矩形对角线的交点,则该反比例函数的解析式是(
)
A.B.
C.
D.
例
3
解析:
C
过点作⊥,
由反比例函数的几何意义可知,△
,
又因为反比例函数图象在第一象限,所以,
由矩形的性质可知△
即
,
解得.
所以,所以
根据图中点的坐标:
(1)求出与的函数解析式;
(2)如果点在双曲线上,求的值.
(3)比较绿色部分和黄色部分的面积的大小.
(3)绿色部分和黄色部分的面积相等,都等于︱︱
答案:(1)
(2)
练一练
随堂训练
1.已知反比例函数下列结论不正确的是(
)
A.图象经过点(1,1)
B.图象在第一、三象限
C.当时,
D.当时,随着的增大而增大
C
2.如图,是反比例函数的图象上的一点,
⊥轴于点,且的面积是3,则的
值是(
)
A.3
B.-3
C.6
D.-6
C
3.函数的图象如图所示,下列结论:
(1)两函数图象的交点坐标为;
(2)当时,;
(3)直线分别与两函数图象交于点两点,则线段的长为3;
(4)当逐渐增大时,的值随着的增大而增大,的值随着的增大而减小.
则其中正确的是(
)
A.只有(1)(2)
B.只有(1)(3)
C.只有(2)(4)
D.只有(1)(3)(4)
D
解:点关于轴的对称点是
∵
点在一次函数的图象上,
∴
∵
点在反比例函数的图象上,∴.
∴
反比例函数的解析式.
课堂小结
反比例函数的图象和性质
形状
反比例函数的图象是由两支双曲线组成的.因此称反比例函数的图象为双曲线;
位置
当时,两支双曲线分别位于第一,三象限内;
当时,两支双曲线分别位于第二,四象限内.
反比例函数比例系数的几何意义
过双曲线
任意一点
分别作
轴、
轴的垂线
,连接
.
则
.
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
