6.3 反比例函数的应用 课件(共24张PPT)
文档属性
| 名称 | 6.3 反比例函数的应用 课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-19 09:22:11 | ||
图片预览








文档简介
(共24张PPT)
北师大版
九年级上
6.3
反比例函数的应用
学习目标
1.能运用反比例函数的概念、性质解决一些实际问题.
2.能从实际问题中寻找变量之间的关系,建立反比例函数模型,解决实际问题.
新课导入
前面我们结合实际问题讨论了反比例函数,看到了反比例函数在分析和解决实际问题中所起的作用,下面,我们进一步探讨如何利用反比例函数解决实际问题.
知识讲解
某校科技小组进行野外考察,利用铺垫木板的方式通过一片烂泥湿地,你能解释他们这样做的道理吗?当人和木板对湿地的压力一定时,随着木板面积S(m2)的变化,人和木板对地面的压强p
(Pa)将如何变化?
如果人和木板对湿地地面的压力合计600N,
那么:
(1)用含S的代数式表示p,p是S的反比例函数吗?为什么?
1.反比例函数在实际生活中的应用
例
1
由p=
得p=
p是S的反比例函数,因为给定一个S的值,对应的就有唯一的一个p值和它对应,根据函数定义,则p是S的反比例函数.
(2)当木板面积为0.2m2时,压强是多少?
当S=0.2m2时,p=
=3000(Pa)
.
答:当木板面积为0.2m2时,压强是3000Pa.
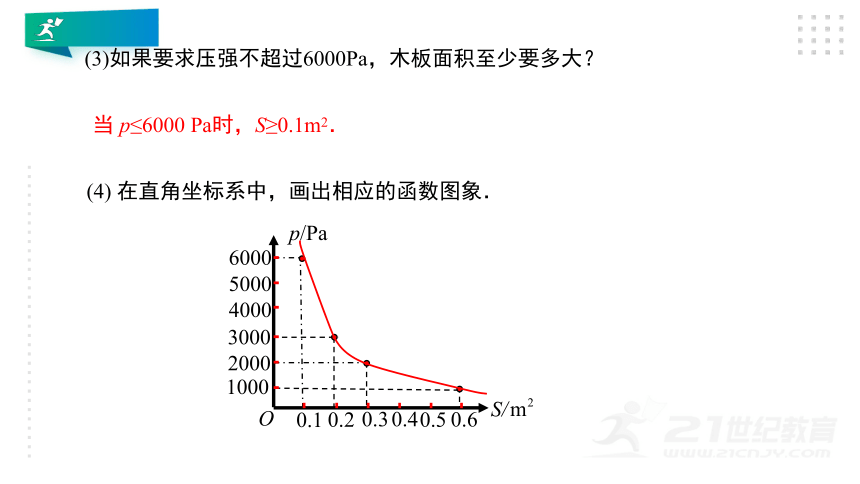
(3)如果要求压强不超过6000Pa,木板面积至少要多大?
(4)
在直角坐标系中,画出相应的函数图象.
当
p≤6000
Pa时,S≥0.1m2.
0.1
0.5
O
0.6
0.3
0.2
0.4
1000
3000
4000
2000
5000
6000
p/Pa
S/
码头工人以每天30吨的速度往一艘轮船上装载货物,
装载完毕恰好用了8天时间.
(1)轮船到达目的地后开始卸货,卸货速度v(单位:吨/天)与卸货时间t(单位:天)之间有怎样的函数关系?
解:由已知得轮船上的货物有30×8=240(吨)
所以v与t的函数解析式为v=
例
2
(2)由于遇到紧急情况,船上的货物必须在不超过5天内卸载完毕,那么平均每天至少要卸多少吨货物?
把t=5代入v=,得
v==48(吨/天).
从结果可以看出,如果全部货物恰好用5天卸载完,那么平均每天卸载48吨,对于函数v=,当t>0时,t越小,v越大.这样若货物不超过5天卸载完,则平均每天至少要卸载48吨.
2.反比例函数在物理问题中的应用
小伟欲用撬棍撬动一块大石头,已知阻力和阻力臂分别为1200N和0.5m.
(1)动力F与动力臂有怎样的函数关系?当动力臂为1.5m时,撬动石头至少需要多大的力?
(2)若想使动力F
不超过题(1)中所用力的一半,则动力臂至少要加长多少?
思考:
用反比例函数的知识解释:在我们使用撬棍时,为什么动力臂越长才越省力?
例
3
解:(1)根据“杠杆原理”得F?=1200×0.5=600,
所以F关于的函数解析式为F=
.
当=1.5m时,F==400(N).
对于函数F=,当=1.5m时,F=400N,此时杠杆平衡.因此,撬动石头至少需要400N的力.
(2)对于函数F=,F随l的增大而减小.因此,只要求出F=200N时对应的值,就能确定动力臂至少加长的量.
当F=400×=200时,由200=得,==3(m),3-1.5=1.5(m).
对于函数F=,当>0时,越大,F越小.因此若想用动力F不超过400N的一半,则动力臂至少要加长1.5m.
练一练
一个用电器的电阻是可调节的,其范围为110~220欧,已知电压为220伏,这个用电器的电路图如图所示.
(1)输出功率与电阻怎样的函数关系?
(2)这个用电器输出功率的范围多大?
解:(1)根据电学知识,当220时,得=
,
①
(2)根据反比例函数的性质可知,电阻越大,功率越小.
把电阻的最小值=110代入①式,得到功率的最大值=
=440(),
把电阻的最大值=220代入①式,得到功率的最小值=
=220(),
因此用电器功率的范围在220到440.
3.反比例函数与一次函数的交点问题
如图,已知反比例函数与一次函数的图象在第一象限相交于
点.
(1)试确定这两个函数的解析式;
(2)求出这两个函数图象的另一个交点的坐标,并根据图象
写出反比例函数的值大于一次函数的值的的取值范围.
例
4
【解】
(1)把点坐标代入反比例函数解析式,得,
∴这两个函数的解析式为和.
解得,
把代入,得
待定系数法确定函数解析式
(2)由方程组
由图象得反比例函数的值大于一次函数的值的的取值范围是:.
交点的坐标满足这个方程组
解得
∴点的坐标为(-2,-1).
随堂训练
B
反比例
=
减小
C
4.
3
4.某中学组织学生到商场参加社会实践活动,他们参与了某种品牌运动鞋的销售工作,已
知该运动鞋每双的进价为120元.为寻求合适的销售价格进行了
4天的试销,试销情况
如下表所示:
?
第1天
第2天
第3天
第4天
150
200
250
300
?
40
30
24
20
(
1)观察表中数据满足什么函数关系?请求出这个函数关系式;
(2
)若商场计划每天的销售利润为3
000元,则其单价应定为多少元?
解:(1)由表中数据可得,=6000,∴y是x的反比例函数,所求函数解析式
=.
(2)由题意,得,将
=代入,可得,
解得=240
经检验,=240是原方程的解.
答:若商场计划每天的销售利润为3000元,则其单价应定为240元.
5.如图,一次函数的图象与反比例函数的图象交于点
,,交轴于点,交轴于点.
(1)求反比例函数和一次函数的解析式;
(2)连接求的面积.
(1)∵反比例函数的图象过点,
∴.
∴
反比例函数的解析式为.
∵
点在反比例函数的图象上,
∴
∴的坐标为.
【解】
∵一次函数的图象经过点,将这两个点的坐标代入,得
解得
∴所求一次函数的解析式为.
(2)∵一次函数的图象交轴于点,
∴
点坐标为,
∴
.
∵点的横坐标为-2,点的横坐标为5,
∴
.
面积分割
课堂小结
实际问题
反比例函数
建立数学模型
运用数学知识解决
https://www.21cnjy.com/help/help_extract.php
北师大版
九年级上
6.3
反比例函数的应用
学习目标
1.能运用反比例函数的概念、性质解决一些实际问题.
2.能从实际问题中寻找变量之间的关系,建立反比例函数模型,解决实际问题.
新课导入
前面我们结合实际问题讨论了反比例函数,看到了反比例函数在分析和解决实际问题中所起的作用,下面,我们进一步探讨如何利用反比例函数解决实际问题.
知识讲解
某校科技小组进行野外考察,利用铺垫木板的方式通过一片烂泥湿地,你能解释他们这样做的道理吗?当人和木板对湿地的压力一定时,随着木板面积S(m2)的变化,人和木板对地面的压强p
(Pa)将如何变化?
如果人和木板对湿地地面的压力合计600N,
那么:
(1)用含S的代数式表示p,p是S的反比例函数吗?为什么?
1.反比例函数在实际生活中的应用
例
1
由p=
得p=
p是S的反比例函数,因为给定一个S的值,对应的就有唯一的一个p值和它对应,根据函数定义,则p是S的反比例函数.
(2)当木板面积为0.2m2时,压强是多少?
当S=0.2m2时,p=
=3000(Pa)
.
答:当木板面积为0.2m2时,压强是3000Pa.
(3)如果要求压强不超过6000Pa,木板面积至少要多大?
(4)
在直角坐标系中,画出相应的函数图象.
当
p≤6000
Pa时,S≥0.1m2.
0.1
0.5
O
0.6
0.3
0.2
0.4
1000
3000
4000
2000
5000
6000
p/Pa
S/
码头工人以每天30吨的速度往一艘轮船上装载货物,
装载完毕恰好用了8天时间.
(1)轮船到达目的地后开始卸货,卸货速度v(单位:吨/天)与卸货时间t(单位:天)之间有怎样的函数关系?
解:由已知得轮船上的货物有30×8=240(吨)
所以v与t的函数解析式为v=
例
2
(2)由于遇到紧急情况,船上的货物必须在不超过5天内卸载完毕,那么平均每天至少要卸多少吨货物?
把t=5代入v=,得
v==48(吨/天).
从结果可以看出,如果全部货物恰好用5天卸载完,那么平均每天卸载48吨,对于函数v=,当t>0时,t越小,v越大.这样若货物不超过5天卸载完,则平均每天至少要卸载48吨.
2.反比例函数在物理问题中的应用
小伟欲用撬棍撬动一块大石头,已知阻力和阻力臂分别为1200N和0.5m.
(1)动力F与动力臂有怎样的函数关系?当动力臂为1.5m时,撬动石头至少需要多大的力?
(2)若想使动力F
不超过题(1)中所用力的一半,则动力臂至少要加长多少?
思考:
用反比例函数的知识解释:在我们使用撬棍时,为什么动力臂越长才越省力?
例
3
解:(1)根据“杠杆原理”得F?=1200×0.5=600,
所以F关于的函数解析式为F=
.
当=1.5m时,F==400(N).
对于函数F=,当=1.5m时,F=400N,此时杠杆平衡.因此,撬动石头至少需要400N的力.
(2)对于函数F=,F随l的增大而减小.因此,只要求出F=200N时对应的值,就能确定动力臂至少加长的量.
当F=400×=200时,由200=得,==3(m),3-1.5=1.5(m).
对于函数F=,当>0时,越大,F越小.因此若想用动力F不超过400N的一半,则动力臂至少要加长1.5m.
练一练
一个用电器的电阻是可调节的,其范围为110~220欧,已知电压为220伏,这个用电器的电路图如图所示.
(1)输出功率与电阻怎样的函数关系?
(2)这个用电器输出功率的范围多大?
解:(1)根据电学知识,当220时,得=
,
①
(2)根据反比例函数的性质可知,电阻越大,功率越小.
把电阻的最小值=110代入①式,得到功率的最大值=
=440(),
把电阻的最大值=220代入①式,得到功率的最小值=
=220(),
因此用电器功率的范围在220到440.
3.反比例函数与一次函数的交点问题
如图,已知反比例函数与一次函数的图象在第一象限相交于
点.
(1)试确定这两个函数的解析式;
(2)求出这两个函数图象的另一个交点的坐标,并根据图象
写出反比例函数的值大于一次函数的值的的取值范围.
例
4
【解】
(1)把点坐标代入反比例函数解析式,得,
∴这两个函数的解析式为和.
解得,
把代入,得
待定系数法确定函数解析式
(2)由方程组
由图象得反比例函数的值大于一次函数的值的的取值范围是:.
交点的坐标满足这个方程组
解得
∴点的坐标为(-2,-1).
随堂训练
B
反比例
=
减小
C
4.
3
4.某中学组织学生到商场参加社会实践活动,他们参与了某种品牌运动鞋的销售工作,已
知该运动鞋每双的进价为120元.为寻求合适的销售价格进行了
4天的试销,试销情况
如下表所示:
?
第1天
第2天
第3天
第4天
150
200
250
300
?
40
30
24
20
(
1)观察表中数据满足什么函数关系?请求出这个函数关系式;
(2
)若商场计划每天的销售利润为3
000元,则其单价应定为多少元?
解:(1)由表中数据可得,=6000,∴y是x的反比例函数,所求函数解析式
=.
(2)由题意,得,将
=代入,可得,
解得=240
经检验,=240是原方程的解.
答:若商场计划每天的销售利润为3000元,则其单价应定为240元.
5.如图,一次函数的图象与反比例函数的图象交于点
,,交轴于点,交轴于点.
(1)求反比例函数和一次函数的解析式;
(2)连接求的面积.
(1)∵反比例函数的图象过点,
∴.
∴
反比例函数的解析式为.
∵
点在反比例函数的图象上,
∴
∴的坐标为.
【解】
∵一次函数的图象经过点,将这两个点的坐标代入,得
解得
∴所求一次函数的解析式为.
(2)∵一次函数的图象交轴于点,
∴
点坐标为,
∴
.
∵点的横坐标为-2,点的横坐标为5,
∴
.
面积分割
课堂小结
实际问题
反比例函数
建立数学模型
运用数学知识解决
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
