2021年新高一分班测试卷（含解析）

本卷由系统自动生成，请仔细校对后使用，答案仅供参考。
吧
中小学教育资源及组卷应用平台
(
学校:___________姓名：___________班级：___________考号：___________
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)2021年新高一分班测试
（考试时间：120分钟
试卷满分：150分）
注意事项：
1．本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。
2．回答第Ⅰ卷时，选出每小题答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动，用橡皮擦干净后，再选涂其他答案标号。写在本试卷上无效。
3．回答第Ⅱ卷时，将答案写在答题卡上。写在本试卷上无效。
4．考试结束后，将本试卷和答题卡一并交回。
2．请将答案正确填写在答题卡上
第I卷（选择题）
一、单选题
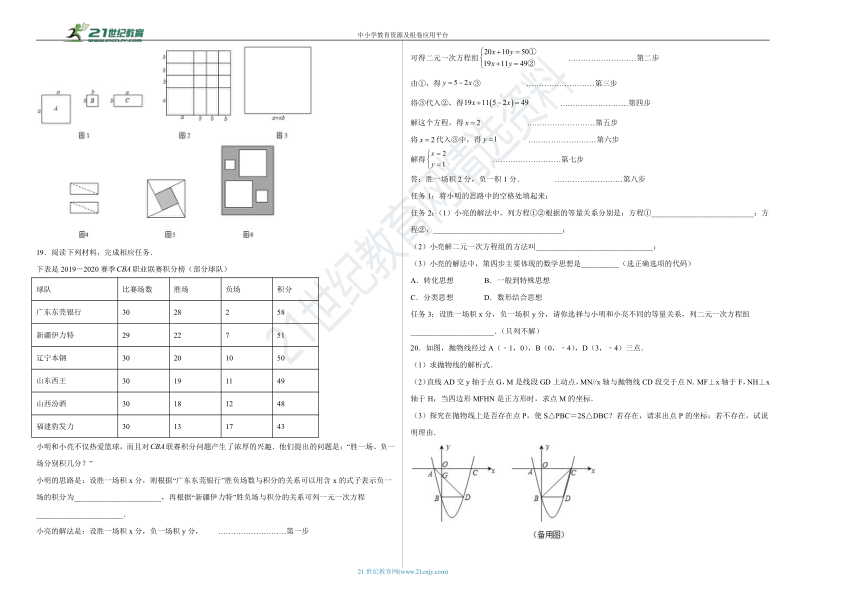
1．如图，现有足够多的型号为①②③的正方形和长方形卡片，如果分别选取这三种型号卡片若干张，可以拼成一个不重叠、无缝隙的长方形，小星想用拼图前后面积之间的关系．解释多项式乘法，则其中②和③型号卡片需要的张数各是（
）
A．3张和7张
B．2张和3张
C．5张和7张
D．2张和7张
2．已知x＝，则x6﹣2x5﹣x4＋x3﹣2x2＋2x﹣的值为（
）
A．0
B．1
C．
D．
3．在数学活动课上，兴趣小组的同学们用4块大小不同的长方形纸板和一块小正方形纸板拼成了一个大正方形，有关数据如图所示，则拼成的大正方形的面积是（　　）
A．20
B．25
C．36
D．49
4．如图1所示，小明（点P）在操场上跑步，操场由两段半圆形弯道和两段直道构成，若小明从点A（右侧弯道起点）出发以顺时针方向沿着跑道行进．设行进的路程为x，小明到右侧半圆形弯道的圆心O的距离PO为y，可绘制出如图2所示函数图象，那么a﹣b的值应为（
）
A．4
B．π﹣1
C．
D．π
5．如图，点E为?ABCD对角线的交点，点B在y轴正半轴上，CD在x轴上，点M为AB的中点．双曲线（x＜0）过点E，M，连接EM．已知，则k的值是（
）
A．﹣8
B．﹣6
C．﹣4
D．﹣2
6．将一张长为8，宽为4的矩形纸片按如下方式进行操作：
（1）如图1，将矩形纸片折叠，使顶点与重合，折痕为，然后展开恢复原状；
（2）沿着图1中虚线段，，，剪开，得到①、②、③、④四个三角形；
（3）将图1中的①、②、③、④这四个三角形拼成如图2的四边形．
则四边形的面积为（
）
A．32
B．25
C．7
D．5
7．如图，在中，在同一平面内，分别以、、为边向形外作等边、等边、等边，若，且，，则（
）
A．
B．
C．
D．
8．在全市中小学校园禁毒安全知识竞赛中，某校八年级（1）班5名同学代表学校参加全市禁毒知识竞赛的决赛．这5名同学的答题得分分别是8.6，8.8，9.2，9.4，9.0，则这5名同学答题得分的平均分和方差分别是（　　）
A．9.1，0.08
B．9.0，0.1
C．9.0，0.08
D．9.1，0.1
9．黄金分割是一种最能引起美感的分割比例，人体结构中有许多比例关系接近黄金比．如图，当人体的下半身长a与身高b的比值越接近黄金比时越美．若图中b为1.7米，则a约为（　　）
A．1.05米
B．1.06米
C．1.07米
D．1.08米
10．某市有6名教师志愿到四川地震灾区的甲、乙、丙三个镇去支教，每人只能去一个镇，则恰好其中一镇去4名，另两镇各去1名的概率为（
）
A．
B．
C．
D．
11．实数在数轴上的位置如图所示，则下列结论正确的是（　　）
A．a+b＞0
B．a﹣b＞0
C．a?b＞0
D．
＞0
12．如图，正方形ABCD中，E是BC边上一点，以E为圆心，EC为半径的半圆与以A为圆心，AB为半径的圆弧外切，则sin∠EAB的值为（
）．
A．
B．
C．
D．
第II卷（非选择题）
二、填空题
13．如图，将大正方形通过剪、割、拼后分解成新的图形，利用等面积法可证明某些乘法公式，在给出的4幅拼法中，其中能够验证平方差公式的有
_________（填序号，多选）．
14．某商场的收银台平均每小时有60个顾客来排队，每位收银员每小时能应付80个顾客，若某天只开设1个收银台，付款开始后4个小时没有顾客排队了，若当天开设2个收银台，开始付款______小时后，没有顾客排队．
15．从蔬菜大棚中收集到50株西红柿秧上小西红柿的个数：
28
62
54
29
32
47
68
27
55
43
36
79
46
54
25
82
16
39
32
64
61
59
67
56
45
74
49
36
39
52
85
65
48
58
59
64
91
67
54
57
68
54
71
26
59
47
58
52
52
70
如果按组距为10将数据分组，组数是
___，频数最大的组处在
___≤x＜___．
16．若是方程的两个根，且，则的值为
______．
三、解答题
17．为了提高玉米产量，进行良种优选．某农业科学院选择了两块基本条件大致相同的试验田用于分析甲、乙两种玉米种子的产量，从两块试验田中各随机抽取了20穗玉米，并对其单穗质量（单位：克）进行整理分析，过程如下：
收集数据：
甲型种子：161
161
172
181
194
201
206
206
211
215
　　215
222
226
232
232
232
242
246
251
254
乙型种子：162
174
183
185
196
207
208
213
215
217
　　219
220
220
220
225
228
236
237
245
250
分析数据：
统计量
型号
平均数
众数
中位数
方差
甲
213
m
215
759.8
乙
213
220
n
536.3
整理数据：
分组
型号
160＜x≤180
180＜x≤200
200＜x≤220
220＜x≤240
240＜x≤260
甲
3
2
6
a
4
乙
2
3
9
4
2
根据以上信息，回答下列问题：
（1）填空：a＝　　，m＝　　，n＝　　．
（2）此次调查中，单穗质量为217克的玉米在单穗质量排名（从高到低）中更靠前的是　　型玉米．
（3）综合以上信息，你认为哪种玉米种子的产量表现更好，请说明理由（写出一条即可）．
18．已知有若干张如图1所示的正方形卡片和长方形卡片，其中A型卡片是边长为a的正方形，B型卡片是边长为b的正方形，C型卡片是长为a，宽为b的长方形．
（1）将1张A型卡片，9张B型卡片，6张C型卡片拼成如图2所示的正方形，请用两种方法表示图2中拼成的正方形的面积，方法一：　
　，方法二：　
　，由此可以得到一个等式：　
　；
（2）选取1张A型卡片，若干张B型卡片，若干张C型卡片无缝无叠合拼成如图3所示的边长为a+nb的正方形，则需要选取B型卡片
　
　张（用含n的式子表示），C型卡片
　
　张（用含n的式子表示）；
（3）将2张C型卡片沿如图4所示虚线剪开后，拼成如图5所示的正方形；将2张A型卡片和2张B型卡片无叠合的置于长为2a+b，宽为a+2b的长方形中（如图6所示）．若图5中阴影部分的面积为4，图6中阴影部分面积为30，记一张A型卡片的面积为SA，一张B型卡片的面积为SB，一张C型卡片的面积为SC，求SA+SB+SC的值．
19．阅读下列材料，完成相应任务．
下表是2019－2020赛季职业联赛积分榜（部分球队）
球队
比赛场数
胜场
负场
积分
广东东莞银行
30
28
2
58
新疆伊力特
29
22
7
51
辽宁本钢
30
20
10
50
山东西王
30
19
11
49
山西汾酒
30
18
12
48
福建豹发力
30
13
17
43
小明和小亮不仅热爱篮球，而且对联赛积分问题产生了浓厚的兴趣．他们提出的问题是：“胜一场、负一场分别积几分？”
小明的思路是：设胜一场积x分，则根据“广东东莞银行”胜负场数与积分的关系可以用含x的式子表示负一场的积分为_______________________，再根据“新疆伊力特”胜负场与积分的关系可列一元一次方程_______________________．
小亮的解法是：设胜一场积x分，负一场积y分，
………………………第一步
可得二元一次方程组
………………………第二步
由①，得③
………………………第三步
将③代入②，得
………………………第四步
解这个方程，得
………………………第五步
将代入③中，得
………………………第六步
解得
………………………第七步
答：胜一场积2分，负一积1分．
………………………第八步
任务1：将小明的思路中的空格处填起来；
任务2：（1）小亮的解法中，列方程①②根据的等量关系分别是：方程①___________________________；方程②：__________________________________；
（2）小亮解二元一次方程组的方法叫_______________________________；
（3）小亮的解法中，第四步主要体现的数学思想是__________（选正确选项的代码）
A．转化思想
B．一般到特殊思想
C．分类思想
D．数形结合思想
任务3：设胜一场积x分，负一场积y分，请你选择与小明和小亮不同的等量关系，列二元一次方程组______________________．（只列不解）
20．如图，抛物线经过A（﹣1，0），B（0，﹣4），D（3，﹣4）三点．
（1）求抛物线的解析式．
（2）直线AD交y轴于点G，M是线段GD上动点，MN//x轴与抛物线CD段交于点N．MF⊥x轴于F，NH⊥x轴于H，当四边形MFHN是正方形时，求点M的坐标．
（3）探究在抛物线上是否存在点P，使S△PBC＝2S△DBC？若存在，请求出点P的坐标；若不存在，试说明理由．
21．已知中，，，，点是线段上一个动点，以为直径的与边交于点，连接．
（1）如图1，证明：；
（2）如图2，当时，判断直线与的位置关系，并说明理由；
（3）如图3，若是边上任意一点，连接，，求面积的最大值．
计算：
；
(2)
.；
（3）已知：，求证：；
（4）已知：，求．
中小学教育资源及组卷应用平台
第1页
共4页
◎
第2页
共4页
21世纪教育网(www.21cnjy.com)
参考答案
1．D
【分析】
分别求出②型号卡片的面积为，③型号卡片的面积为，再观察多项式即可得解；
【详解】
②型号卡片的面积为，③型号卡片的面积为，
∵，
∴需要②型号卡片2张，③型号卡片7张；
故答案选D．
【点睛】
本题主要考查了多项式乘以多项式，准确计算是解题的关键．
2．C
【分析】
对已知进行变形，再代入所求式子，反复代入即可．
【详解】
，
，
，
，
，
，
，
，
，
故选：C
【点睛】
本题主要考查了二次根式的化简求值，对所求式子进行变形，反复代入x的值即可解决．
3．C
【分析】
设小正方形的边长为，根据大正方形的边长相等可得方程，解得，进而求得大正方形的边长及面积
【详解】
设小正方形的边长为，根据大正方形的边长相等可得：
解得
大正方形的边长为
大正方形面积为
故选C
【点睛】
本题考查了一元一次方程的应用，找到等量关系列方程是解题的关键．
4．D
【分析】
设两段半圆的半径为r，根据图象解答即可．
【详解】
解：设两段半圆的半径为r，根据题意得：
当0≤x≤π时，y=b=r，
当x=π，即小明到左侧半圆弧线中点时，y=a=π+r，
∴a-b=π+r-r=π．
故选：D．
【点睛】
本题考查了动点函数的图象问题，解决本题的关键是利用数形结合的思想解答问题．
5．B
【分析】
把三角形AEM的面积用E、M的坐标表示出来，然后根据双曲线过E、M两点及E、M纵坐标的关系可以得到解答．
【详解】
解：由已知条件可得：
SΔAEM=，
∵由已知可得：yM=2yE，
∴，
∴，
∴xM×yM=-6，即k=-6，
故选B．
【点睛】
本题考查反比例函数的综合应用，熟练掌握反比例函数的解析式和性质、平行四边形的性质及三角形面积的求法是解题关键．
6．D
【分析】
先说明四边形ABCD为菱形可得BC=CD、AC⊥BD,OD=BD，设BC=CD=x，则BC=8-x,再运用勾股定理列方程求出x；然后用勾股定理求出BD，进而求出OD，由图2可得小正方形的边长，最后求面积即可．
【详解】
解：∵四边形ABCD为菱形
∴BC=CD、AC⊥BD,OD=BD
设BC=CD=x，则BC=8-x,
在Rt△DCH中，CD2=CH2+DH2,即x2=（8-x）2+42，解得x=5
在Rt△DBH中，BD=
,
∴OD=
在Rt△DCO中，OC=
∴图2中小正方形的边长为2-=
∴图2中小正方形的面积为5．
故选D．
【点睛】
本题主要考查了矩形的性质、菱形的性质以及勾股定理的应用，灵活应用勾股定理成为解答本题的关键．
7．C
【分析】
分别求出等边三角形ABE和BCF的面积，根据求出AC的长，再根据勾股定理逆定理判断△是直角三角形，再根据面积公式求结论即可．
【详解】
解：如图1，
在等边三角形中，当边长为2a时，高为，用此结论可得：
∵为等边三角形，
∴高为
∴
∵为等边三角形，
∴高为
∴
∴
即：
解得：
在△中，
∴△是直角三角形，
∴
故选：C．
【点睛】
此题主要考查了等边三角形的性质，勾股定理及其逆定理，三角形面积公式等知识，AC=5是解答此题的关键．
8．C
【分析】
根据算术平均数和方差的定义列式计算即可．
【详解】
解：这5名同学答题得分的平均分＝9.0，
其方差为×[（8.6﹣9.0）2+（8.8﹣9.0）2+（9.2﹣9.0）2+（9.4﹣9.0）2+（9.0﹣9.0）2]＝0.08，
故选：C．
【点睛】
本题主要考查方差和算术平均数，解题的关键是掌握方差和算术平均数的定义．
9．A
【分析】
把一条线段分成两部分，使其中较长的线段为全线段与较短线段的比例中项，这样的线段分割叫做黄金分割，他们的比值叫做黄金比．
【详解】
解：∵人体的下半身长a与身高b的比值越接近黄金比时越美，
∴≈0.618，
∴a≈0.618b＝0.618×1.7≈1.05（米），
故选：A．
【点睛】
本题考查了黄金分割的概念，熟练掌握黄金比是解答本题的关键．
10．B
【分析】
因为对于这六个人来说，会被随机分派到3个镇中的任何一个，所以一共有种情况，而有4个人的镇可能是3个镇中的任何一个，剩下两个镇各派一个人的派法是，根据概率公式求解．
【详解】
解：6名教师志愿随机派到3个镇中的任何一个共有种情况，有4个人的镇可能是3个镇中的任何一个，另两镇各去1名的结果数为，
所以恰好其中一镇去4名，另两镇各去1名的概率，
故选：B．
【点评】
选出符合事件或的结果数目，然后根据概率公式求出事件A或的概率．
11．A
【解析】
【分析】
由题意可知，所以异号，且，根据有理数加减法得的值应取b的符号，故，根据其大小，能够判断出，所以，根据有理数的乘法法则可知，从而求得结果.
【详解】
依题意得：，所以异号，且，所以，
，故选A.
【点睛】
该题考查的是有关实数的运算法则问题，涉及到的知识点有异号的两个实数的和的符号与绝对值大的那个数保持一致，两个异号的实数的积与商是小于零的，而两个实数的差的符号与两个实数的大小有关，从而求得结果.
12．B
【解析】
【分析】
利用勾股定理和锐角三角函数的定义、两圆相外切，圆心距等于两圆半径的和.
【详解】
设正方形的边长为y，，
由题意知，，即，
由于，化简得，
所以，故选B.
【点睛】
该题考查的是有关角的正弦值的问题，涉及到的知识点有锐角三角函数的定义，勾股定理，两圆相切的条件，利用题中的条件，建立相应的等量关系，求得结果.
13．①②③
【分析】
分别在两个图形中表示出阴影部分的面积，或者用两种方法表示同一个图形的面积，继而可得出验证公式．
【详解】
解：在图①中，左边的图形阴影部分的面积＝a2﹣b2，右边图形中阴影部分的面积＝（a+b）（a﹣b），故可得：a2﹣b2＝（a+b）（a﹣b），可以验证平方差公式；
在图②中，除右下角阴影部分的面积外，剩余部分的面积可以表示为a2﹣b2，也可以表示为（a﹣b）（a+b），故可得：a2﹣b2＝（a+b）（a﹣b），可以验证平方差公式；
在图③中，左边的图形阴影部分的面积＝a2﹣b2，右边图形中阴影部分的面积＝（a+b）（a﹣b），故可得：a2﹣b2＝（a+b）（a﹣b），可以验证平方差公式；
在图④中，阴影部分的面积可以表示为（a+b）2﹣4ab，也可以表示为（a﹣b）2，由此可得（a+b）2﹣4ab＝（a﹣b）2，没法验证平方差公式．
故答案为：①②③．
【点睛】
本题主要考查了平方差公式，运用不同方法表示阴影部分面积是解题的关键．本题主要利用面积公式来证明a2﹣b2＝（a+b）（a﹣b）．
14．0.8
【分析】
首先求出开始付款时有多少人排队，再设付款开始x小时后没有顾客排队，列出方程，解之即可．
【详解】
解：设每小时排队付款的人数为1份，
则刚开始付款时排队的人数是：80×4-4×60=80人，
即开始付款时已经有80人在排队，
设付款开始x小时后没有顾客排队，根据题意可得方程：
80×2×x=80+60x，
解得：x=0.8，
故答案为：0.8．
【点睛】
此题主要考查了一元一次方程的应用，根据题干得出开始付款时等待的有80人是解决本题的关键，由此抓住每小时增加的人数和2台收银台的工作效率即可列出符合题意的方程解决问题．
15．8，
46，
56
【分析】
根据极差和组距，可以判断组数，确定分点后，列频数分布表进行统计即可；再将频数分布表中的数据用频数分布直方图表示出来，最后从图表中观察整体的情况，得出结论．
【详解】
解：最大值是91，最小值为16，极差为91﹣16＝75，若组距为10，则分为8组，
分组
16≤x＜26
26≤x＜36
36≤x＜46
46≤x＜56
56≤x＜66
66≤x＜76
76≤x＜86
86≤x＜96
个数
2
6
6
13
12
7
3
1
频数最大的组处在
46≤x＜56．
故答案为：8，46，56．
【点睛】
本题考查频数分布表，数据的表示，频数分布表和频数分布直方图能较好的反映出一组数据整体情况．
【解析】
16.【分析】
由一元二次方程根与系数的关系得到韦达定理，然后解出，并结合根的判别式进行取舍即可.
【详解】
解：因为是方程的两个根
所以，，
又因为
所以，即
解得或
又因为，即
所以
故答案为：1.
17．（1）5，232，218；（2）甲；（3）乙型玉米种子的产量表现更好，理由见解析．
【分析】
（1）将甲型种子抽样20穗质量进行分组统计，进而得出a的值，利用中位数、众数的意义求出m、n的值；
（2）从中位数的角度得出结论；
（3）根据乙型种子单穗质量的中位数大于甲型种子单穗质量的中位数可说明乙型玉米种子的产量表现更好．
【详解】
解：（1）将甲型种子抽样20穗质量进行分组统计，可得220＜x≤240的频数为5，即a＝5，
甲型种子抽样20穗质量出现次数最多的是232，共出现3次，因此众数为232，即m＝232，
将乙型种子抽样20穗质量从小到大排列后，处在中间位置的两个数的平均数为＝218，即中位数是218，也就是n＝218，
故答案为：5，232，218；
（2）∵甲：217＞中位数215，乙：217＜中位数218，
∴单穗质量为217克的玉米在单穗质量排名（从高到低）中更靠前的是甲型玉米，
故答案为：甲；
（3）乙型玉米种子的产量表现更好，
理由：乙型种子单穗质量的中位数大于甲型种子单穗质量的中位数，说明乙型种子大部分质量高于甲型种子．
【点睛】
本题考查频数分布表，中位数、众数、方差的意义，理解中位数、众数、方差的意义，掌握中位数、众数、方差的计算方法是正确解答的前提．
18．（1）（a+3b）?，a?+6ab+9b?，（a+3b）?＝a?+6ab+9b?；（2）n?，2n；（3）22
【分析】
（1）利用整体法和分割法：将正方形看成整体，面积是边长的平方；将正方形分成A、B、C三种图形面积的和，建立等量关系求解；
（2）正方形的边长为a+nb时，则有一个A型，横方向和纵方向分别有B型图形n个，C型为n×n；
（3）利用三种图形的面积分别表示图5和图6的阴影部分的面积，利用整体代入法，进而求得答案．
【详解】
解：（1）图2，正方形边长（a+3b），面积（a+3b）?，正方形中有一个A，六个B，九个C，面积（a?+6ab+9b?）．所得等式（a+3b）?＝a?+6ab+9b?，
故答案为：（a+3b）?，a?+6ab+9b?，（a+3b）?＝a?+6ab+9b?；
（2）正方形边长为（a+nb），横、纵各有n个C型，故C型数量2n，B型数量为n×n＝n?，
故答案为：n?，2n；
（3）∵图5中阴影部分的面积为4，
∴，
∴，
∵图6中阴影部分面积为30，
∴，
化简得，
将代入，
得：，
解得：，
∴．
【点睛】
本题主要考查：利用面积相等建立等量关系，解决本题的关键是能够分割图形，了解各个部分组成，便可表示各个类型的数量．善用整体代入法，表示出相应部分面积，利用整体代入法求解．
19．任务1：，
任务2：（1）辽宁本钢队胜20场积分＋负10场积分，共积50分；山东西王队胜19场积分＋负11场积分，共积49分；
（2）代入消元法；
（3）A
任务3：
【分析】
任务1:利用总积分减去28胜所得到的积分除以负的场数即可，因为胜、负都以用来表示后，根据“新疆伊力特”胜、负场和所获得的积分建立等式即可；
任务2：（1）读取表中相关信息即可得出所列方程所选的等量关系；
（2）根据计算过程将一个式子整理代入另一个式子来消元的过程叫代入消元法；
（3）体现了将二元一次方程转化为一元一次方程的数学思想中的转化思想；
任务3:小明和小亮选了前四组，按要求选择与小明和小亮不同的等量关系，我们可以选择山西汾酒、福建豹发力两组数据．
【详解】
解：任务1：设负一场积分，
由题意可得等式：，
解得：，
根据新疆伊力特胜２２场，负７场，积分５１，
建立等式得：
故答案是：，．
任务2：（1）辽宁本钢队胜20场积分＋负10场积分，共积50分；山东西王队胜19场积分＋负11场积分，共积49分；
（2）根据计算过程记得判断出是：代入消元法；
故答案是：代入消元法．
（3）体现了将二元一次方程转化为一元一次方程的数学思想中的转化思想；
故选：A．
任务3：设胜一场积x分，负一场积y分，根据“山西汾酒”积分和“福建豹发力”积分可得，
【点睛】
本题考查了二元一次方程、解二元一次方程的方法、解题的关键是能根据题中信息引进未知量建立相应等量关系．
20．（1）y＝x2+﹣3x﹣4；（2）M（，）；（3）点P的坐标为（2，4）或（2，4），见解析．
【分析】
（1）将已知的点代入解析式列方程组求解即可；
（2）利用待定系数法先求出直线AD的解析式，设M点横坐标为n，根据点在直线AD上，用含n的式子表示纵坐标，由MN//x轴与抛物线CD段交于点N，用含n的式子表示N点坐标，根据正方形的性质列方程分求解即可；
（3）先求出B、C两点，求出直线BC的解析式和S△DBC的面积，①当点Р在直线BC的上方时，
若存在点P，满足S△PBC＝2S△DBC，过点Р作PQ//BC交y轴于点Q，则S△QBC＝S△PBC＝2S△DBC＝2S△EBC，可得BQ＝2BE＝6，求出Q点，继而求出PQ的解析式为y＝x+2，由x2﹣3x﹣4＝x+2，得x2﹣4x﹣6＝0，解得x＝2或x＝2，②当点Р在直线BC下方时，同理可得，PQ的解析式为y＝x﹣10，由x2﹣3x﹣4＝x﹣10，得x2﹣4x+6＝0，方程无实数解，这时点Р不存在.
【详解】
解：（1）设抛物线解析式为y＝ax2+bx﹣4（a≠0），
将A，D两点代入解析式得：
，
解得a＝1，b＝﹣3，
∴抛物线解析式为y＝x2+﹣3x﹣4；
（2）四边形MNHF是矩形，当MF＝HF时，四边形MNHF是正方形，
设直线AD的解析式为y＝kx+m
（k≠0）．
将A，D两点的坐标代入y＝kx+m，
得：，
解得，
∴直线AD的解析式为y＝﹣x﹣1，
设M（n，﹣n﹣1），
∴FH＝MF＝|﹣n﹣1|＝n+1，
∴OH＝n+n+1＝2n+1，
∵MN//x轴，
∴N（2n+1，﹣n﹣1），
∴（2n+1）2﹣3（2n+1）﹣4＝﹣n﹣1，
整理得
4n2﹣n﹣5＝0，
解得，n2＝﹣1（负值，舍去），
∴M（，）；
（3）如图，在抛物线上存在点P，使S△PBC＝2S△DBC，
①当点Р在直线BC的上方时，
由（1）知，当x2﹣3x﹣4＝0时，有x＝﹣1或x＝4，
∴C（4，0），
又∵B（0，﹣4），
∴BC的解析式为y＝x﹣4，
经过点D（3，﹣4）与BC平行的直线DE解析式为y＝x﹣7，
∴BE＝3，
若存在点P，满足S△PBC＝2S△DBC，过点Р作PQ//BC交y轴于点Q，则S△QBC＝S△PBC＝2S△DBC＝2S△EBC，
∴BQ＝2BE＝6，
∴Q（0，2），
∴PQ的解析式为y＝x+2，
由x2﹣3x﹣4＝x+2，得x2﹣4x﹣6＝0，
解得x＝2或x＝2，
∴x2﹣3x﹣4＝x+2＝4或x2﹣3x﹣4＝x+2＝4，
这时点Р的坐标为（2，4）或（2，4），
②当点Р在直线BC下方时，同理可得，PQ的解析式为y＝x﹣10，
由x2﹣3x﹣4＝x﹣10，得x2﹣4x+6＝0，方程无实数解，这时点Р不存在，
综上，点P的坐标为（2，4）或（2，4）．
【点睛】
本题主要考查一次函数、二次函数与几何图形综合，解决本题的关键是要熟练掌握一次函数、二次函数图象性质和几何图形的性质.
21.．（1）证明见解析；（2）与相切，证明见解析；（3）．
【分析】
（1）利用勾股定理的逆定理，得到，利用“直径所对的圆周角是直角”，得到，再利用“同位角相等，两直线平行”，得到；
（2）过作于，只需要证明等于半径，即可得到与相切，先由，可得到直径的长度，因为，所以，由此得到的长度，过作垂直于于，则可求，所以可求，还可以证明四边形为矩形，所以可求，得到，即可证明是圆切线；
（3）因为，所以∽，则，设，则可以用表示，由，可以用表示，因为，所以的面积为，得到一个关于的二次函数，直接在顶点处取得最大值．
【详解】
（1）证明：∵，，，
∴，
∴，
∵是直径，
∴，
∴，
∴；
（2）解：
与相切，理由如下：
如图，
过作于，于，
∵，
∴，
∴，
∵，
∴，
即，
∴，
则，
∴，
∵，，
∴，
∴四边形为矩形，
∴，
∴，
又，
∴是的切线；
（3）如图，
∵，
∴∽，
∴，
设，
∴，
∴，
∵，，
∴，
∴当时，最大值为，
即的面积最大值为．
【点睛】
本题考查圆的综合题、涉及直径所对的圆周角是90°、平行线的判定方法、切线的判定、平行线分线段成比例、矩形的判定、相似三角形的判定与性质、配方法求最值、函数思想、方程思想、几何直观、运算能力等，是重要考点，掌握相关知识是解题关键.
22.(1)
(2)
【解析】
【分析】
（1）由平方差和完全平方公式化简即可；
（2）先分子分母约去，再通分化简即可得解.
【详解】
(1)原式＝.
(2)原式＝
＝.
【点睛】
本题主要考查了平方差、完全平方公式，考查了学生的化简能力，属于基础题.
（3）【解析】
【分析】
利用结合律，将方程左边化简为，进而得证.
【详解】
左边右边，故原式成立．
【点睛】
本题主要考查了代数式的化简问题，属于基础题.
（4）．-3
【解析】
【分析】
利用乘法分配律展开，利用条件化简即可得解.
【详解】
原式.
【点睛】
本题主要考查了乘法的分配律及加法的结合律，属于基础题
答案第1页，总2页
21世纪教育网(www.21cnjy.com)