考前最后一轮基础知识巩固之第二章 第1课 函数的概念
文档属性
| 名称 | 考前最后一轮基础知识巩固之第二章 第1课 函数的概念 |
|
|
| 格式 | zip | ||
| 文件大小 | 151.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | |||
| 科目 | 数学 | ||
| 更新时间 | 2012-06-05 00:00:00 | ||
图片预览


文档简介
第1课 函数的概念
【考点导读】
1.在体会函数是描述变量之间的依赖关系的重要数学模型的基础上,通过集合与对应的语言刻画函数,体会对应关系在刻画函数概念中的作用;了解构成函数的要素,会求一些简单函数的定义域和值域.
2.准确理解函数的概念,能根据函数的三要素判断两个函数是否为同一函数.
【基础练习】
1.设有函数组:①,;②,;③,;④,;⑤,.其中表示同一个函数的有___②④⑤___.
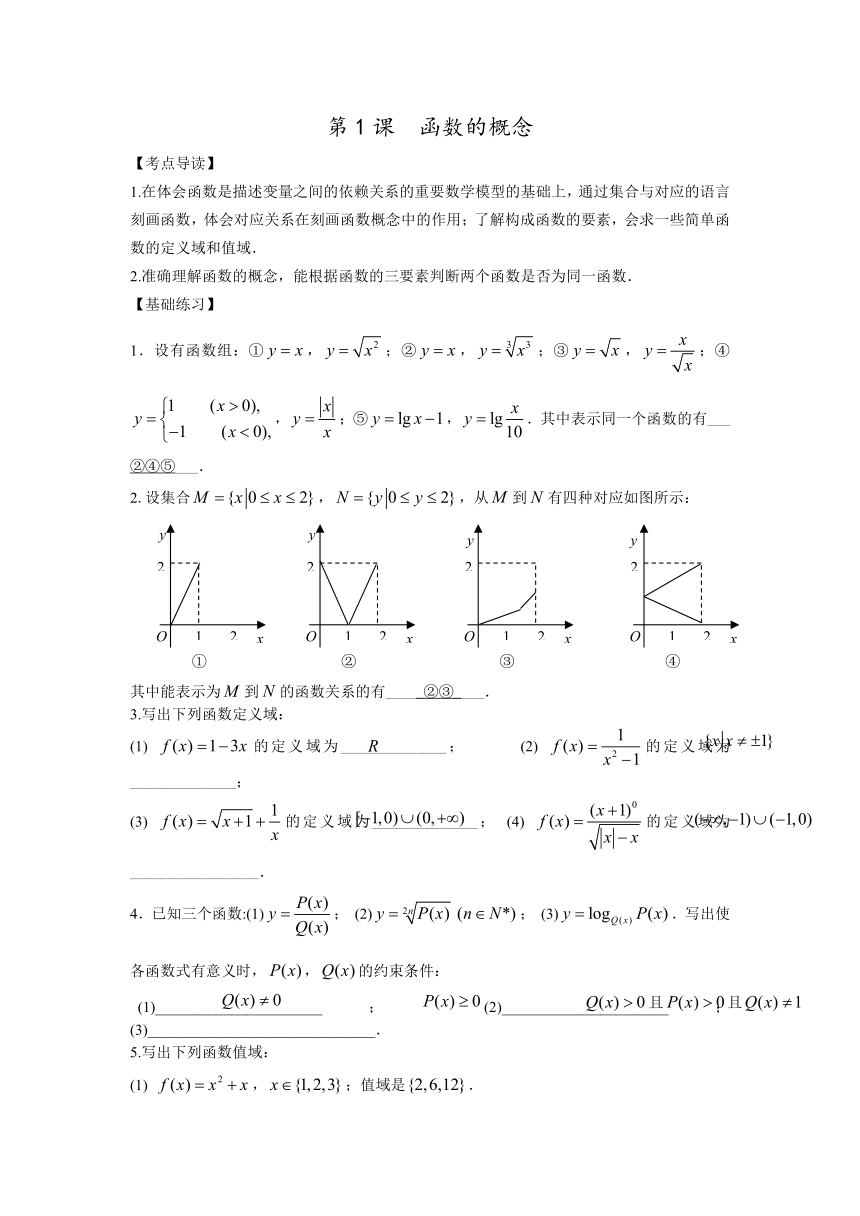
2.设集合,,从到有四种对应如图所示:
其中能表示为到的函数关系的有_____②③____.
3.写出下列函数定义域:
(1) 的定义域为______________; (2) 的定义域为______________;
(3) 的定义域为______________; (4) 的定义域为_________________.
4.已知三个函数:(1); (2); (3).写出使各函数式有意义时,,的约束条件:
(1)______________________; (2)______________________; (3)______________________________.
5.写出下列函数值域:
(1) ,;值域是.
(2) ;值域是.
(3) ,.值域是.
【范例解析】
例1.设有函数组:①,;②,;③,;④,.其中表示同一个函数的有③④.
分析:判断两个函数是否为同一函数,关键看函数的三要素是否相同.
解:在①中,的定义域为,的定义域为,故不是同一函数;
在②中,的定义域为,的定义域为,故不是同一函数;
③④是同一函数.
点评:两个函数当它们的三要素完全相同时,才能表示同一函数.而当一个函数定义域和对应法则确定时,它的值域也就确定,故判断两个函数是否为同一函数,只需判断它的定义域和对应法则是否相同即可.
例2.(1)求下列函数的定义域:① ; ② ;
(2)设函数,则函数的定义域为_____________.
分析:(2)先求的定义域,得不等式组求解.
解:(1)① 由题意得:解得且或且,
故定义域为.
② 由题意得:,解得,故定义域为.
(2)由,解得,则
故的定义域为.
点评:(1)确定函数的定义域主要根据是使式子有意义,列出不等式(组)求解;(2)已知函数的定义域为,求函数的定义域问题,由解出x的范围.
例3.若函数的定义域为R,求实数a的取值范围.
分析:化归为恒成立问题.
解:由对任意恒成立,
当时,成立; 当时,不成立;
当时,,解得.
综上,实数a的取值范围是.
点评:注意讨论二次项系数的情况.
例4.求下列函数的值域:
(1),;
(2);
(3).
分析:运用配方法,逆求法,换元法等方法求函数值域.
解:,,函数的值域为;
解法一:由,,则,,故函数值域为.
解法二:由,则,,,,故函数值域为.
(3)解:令,则,,
当时,,故函数值域为.
点评:二次函数或二次函数型的函数求值域可用配方法;逆求法利用函数有界性求函数的值域;用换元法求函数的值域应注意新元的取值范围.
【反馈演练】
1.函数f(x)=的定义域是___________.
2.函数的定义域为_________________.
3. 函数的值域为________________.
4. 函数的值域为_____________.
5.函数的定义域为_____________________.
6.若函数的定义域为R,则实数的取值范围______________.
7.设,则的定义域为______________.
8.设,函数在区间上的最大值与最小值之差为,则____4___.
9. 设集合对任意实数x恒成立},则下列结论中:
①PQ ;②QP;③P=Q;④PQ=.
其中正确结论的序号有______①______.
10. 已知函数与分别由下表给出:
x 1 2 3 4
f(x) 2 3 4 1
x 1 2 3 4
g(x) 2 1 4 3
(1)求的值; (2)若2时,求的值;
(3)求满足的的值.
解:(1);(2) 4; (3)1,4
11.记函数f(x)=的定义域为A,g(x)=lg[(x-a-1)(2a-x)](a<1) 的定义域为B.
(1) 求A;
(2) 若BA,求实数a的取值范围.
解:(1)由2-≥0,得≥0,x<-1或x≥1, 即A=(-∞,-1)∪[1,+ ∞) .
(2) 由(x-a-1)(2a-x)>0,得(x-a-1)(x-2a)<0.
∵a<1,∴a+1>2a,∴B=(2a,a+1) .
∵BA, ∴2a≥1或a+1≤-1,即a≥或a≤-2,而a<1,
∴≤a<1或a≤-2,故当BA时, 实数a的取值范围是(-∞,-2]∪[,1).
12.对定义域分别是,的函数,,规定:函数
(1)若函数,,,,写出函数的解析式;
(2)求问题(1)中函数的值域.
解:(1)
(2)当时,;当时,;当时,;
综上可知,.
y
1
2
2
x
O
②
1
2
2
x
y
O
①
1
2
2
x
O
③
y
1
2
2
x
O
④
y
且且
【考点导读】
1.在体会函数是描述变量之间的依赖关系的重要数学模型的基础上,通过集合与对应的语言刻画函数,体会对应关系在刻画函数概念中的作用;了解构成函数的要素,会求一些简单函数的定义域和值域.
2.准确理解函数的概念,能根据函数的三要素判断两个函数是否为同一函数.
【基础练习】
1.设有函数组:①,;②,;③,;④,;⑤,.其中表示同一个函数的有___②④⑤___.
2.设集合,,从到有四种对应如图所示:
其中能表示为到的函数关系的有_____②③____.
3.写出下列函数定义域:
(1) 的定义域为______________; (2) 的定义域为______________;
(3) 的定义域为______________; (4) 的定义域为_________________.
4.已知三个函数:(1); (2); (3).写出使各函数式有意义时,,的约束条件:
(1)______________________; (2)______________________; (3)______________________________.
5.写出下列函数值域:
(1) ,;值域是.
(2) ;值域是.
(3) ,.值域是.
【范例解析】
例1.设有函数组:①,;②,;③,;④,.其中表示同一个函数的有③④.
分析:判断两个函数是否为同一函数,关键看函数的三要素是否相同.
解:在①中,的定义域为,的定义域为,故不是同一函数;
在②中,的定义域为,的定义域为,故不是同一函数;
③④是同一函数.
点评:两个函数当它们的三要素完全相同时,才能表示同一函数.而当一个函数定义域和对应法则确定时,它的值域也就确定,故判断两个函数是否为同一函数,只需判断它的定义域和对应法则是否相同即可.
例2.(1)求下列函数的定义域:① ; ② ;
(2)设函数,则函数的定义域为_____________.
分析:(2)先求的定义域,得不等式组求解.
解:(1)① 由题意得:解得且或且,
故定义域为.
② 由题意得:,解得,故定义域为.
(2)由,解得,则
故的定义域为.
点评:(1)确定函数的定义域主要根据是使式子有意义,列出不等式(组)求解;(2)已知函数的定义域为,求函数的定义域问题,由解出x的范围.
例3.若函数的定义域为R,求实数a的取值范围.
分析:化归为恒成立问题.
解:由对任意恒成立,
当时,成立; 当时,不成立;
当时,,解得.
综上,实数a的取值范围是.
点评:注意讨论二次项系数的情况.
例4.求下列函数的值域:
(1),;
(2);
(3).
分析:运用配方法,逆求法,换元法等方法求函数值域.
解:,,函数的值域为;
解法一:由,,则,,故函数值域为.
解法二:由,则,,,,故函数值域为.
(3)解:令,则,,
当时,,故函数值域为.
点评:二次函数或二次函数型的函数求值域可用配方法;逆求法利用函数有界性求函数的值域;用换元法求函数的值域应注意新元的取值范围.
【反馈演练】
1.函数f(x)=的定义域是___________.
2.函数的定义域为_________________.
3. 函数的值域为________________.
4. 函数的值域为_____________.
5.函数的定义域为_____________________.
6.若函数的定义域为R,则实数的取值范围______________.
7.设,则的定义域为______________.
8.设,函数在区间上的最大值与最小值之差为,则____4___.
9. 设集合对任意实数x恒成立},则下列结论中:
①PQ ;②QP;③P=Q;④PQ=.
其中正确结论的序号有______①______.
10. 已知函数与分别由下表给出:
x 1 2 3 4
f(x) 2 3 4 1
x 1 2 3 4
g(x) 2 1 4 3
(1)求的值; (2)若2时,求的值;
(3)求满足的的值.
解:(1);(2) 4; (3)1,4
11.记函数f(x)=的定义域为A,g(x)=lg[(x-a-1)(2a-x)](a<1) 的定义域为B.
(1) 求A;
(2) 若BA,求实数a的取值范围.
解:(1)由2-≥0,得≥0,x<-1或x≥1, 即A=(-∞,-1)∪[1,+ ∞) .
(2) 由(x-a-1)(2a-x)>0,得(x-a-1)(x-2a)<0.
∵a<1,∴a+1>2a,∴B=(2a,a+1) .
∵BA, ∴2a≥1或a+1≤-1,即a≥或a≤-2,而a<1,
∴≤a<1或a≤-2,故当BA时, 实数a的取值范围是(-∞,-2]∪[,1).
12.对定义域分别是,的函数,,规定:函数
(1)若函数,,,,写出函数的解析式;
(2)求问题(1)中函数的值域.
解:(1)
(2)当时,;当时,;当时,;
综上可知,.
y
1
2
2
x
O
②
1
2
2
x
y
O
①
1
2
2
x
O
③
y
1
2
2
x
O
④
y
且且
同课章节目录
