考前最后一轮基础知识巩固之第二章 第11课 函数模型及其应用
文档属性
| 名称 | 考前最后一轮基础知识巩固之第二章 第11课 函数模型及其应用 |  | |
| 格式 | zip | ||
| 文件大小 | 159.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | |||
| 科目 | 数学 | ||
| 更新时间 | 2012-06-05 06:39:59 | ||
图片预览


文档简介
第11 课 函数模型及其应用
【考点导读】
1.能根据实际问题的情境建立函数模型,结合对函数性质的研究,给出问题的解答.
2.理解数据拟合是用来对事物的发展规律进行估计的一种方法,会根据条件借助计算工具解决一些简单的实际问题.
3.培养学生数学地分析问题,探索问题,解决问题的能力.
【基础练习】
1.2006年11月15日起,国内投寄首重100g以内的外部信函的邮资标准:每封信不超过20g时付邮资120分,超过20g而不超过40g付邮资240分,超过40g而不超过60g付邮资360分,依次类推.如果某人所寄一封信的质量为82.5g,那么他应付邮资为____600___分.
2.今有一组实验数据如下:
1.99 3.0 4.0 5.1 6.12
1.5 4.04 7.5 12 18.01
现准备用下列函数中的一个近似地表示这些数据满足的规律,
① ② ③ ④
其中最接近的一个的序号是______③_______.
3.以墙为一边,用篱笆围成长方形的场地,并用平行于一边的篱笆隔开(如图),已知篱笆的总长为定值l,
则这块场地的最大面积是___________.
4.某种放射性物质不断变化为其他物质,每经过1年,这种物质剩留的质量是原来的84%,则这种物质的
剩留量关于时间的函数关系式为_______________.
5.某摩托车生产企业,上年度生产摩托车的投入成本为1万元/辆,出厂价为1.2万元/辆,年销售量为1000辆.本年度为适应市场需求,计划提高产品档次,适度增加投入成本.若每辆车投入成本增加的比例为x(0 < x < 1),则出厂价相应的提高比例为0.75x,同时预计年销售量增加的比例为0.6x.已知年利润 = (出厂价-投入成本)×年销售量.
(Ⅰ)写出本年度预计的年利润y与投入成本增加的比例x的关系式;
(Ⅱ)为使本年度的年利润比上年有所增加,问投入成本增加的比例x应在什么范围内?
解:(Ⅰ)由题意得y = [ 1.2×(1+0.75x)-1×(1 + x) ] ×1000×( 1+0.6x )(0 < x < 1)
整理得 y = -60x2 + 20x + 200(0 < x < 1).
(Ⅱ)要保证本年度的利润比上年度有所增加,当且仅当
即 解不等式得.
答:为保证本年度的年利润比上年度有所增加,投入成本增加的比例x应满足0 < x < 0.33.
【范例解析】
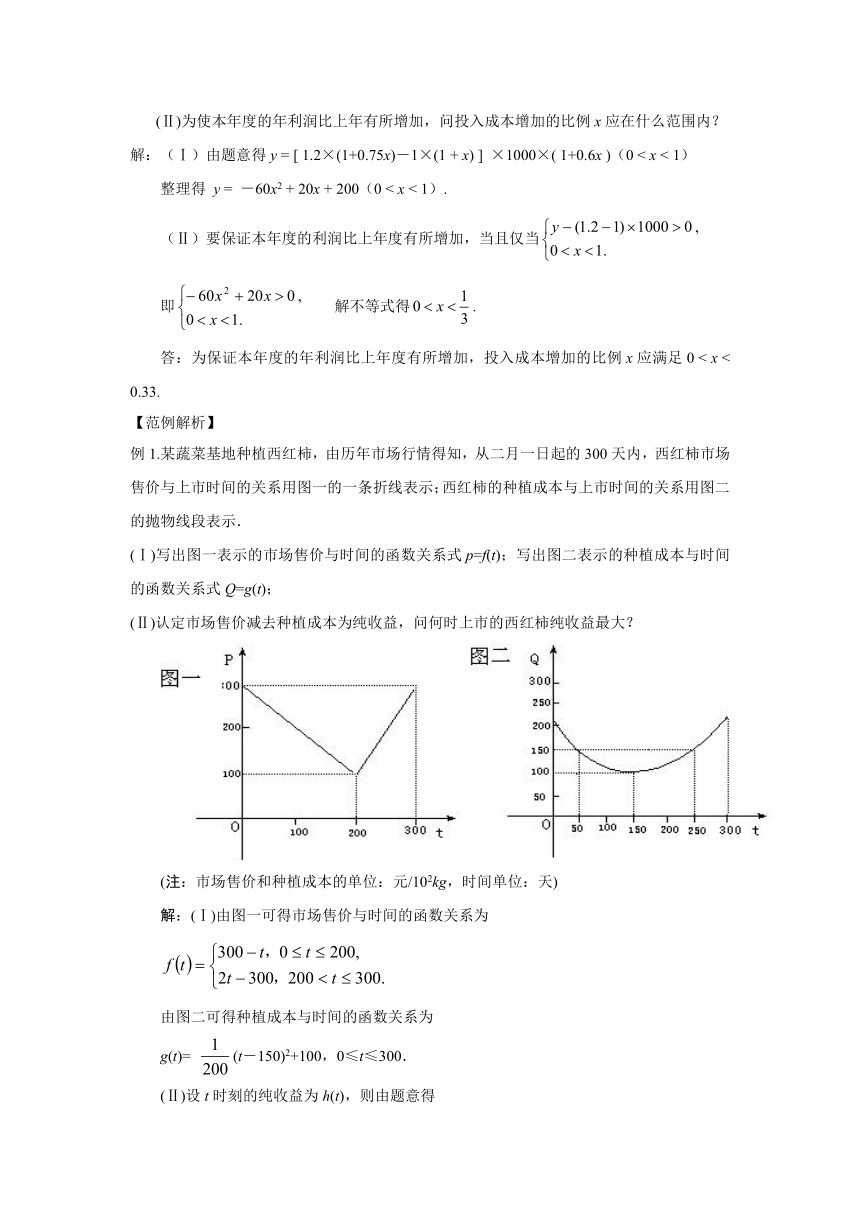
例1.某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的300天内,西红柿市场售价与上市时间的关系用图一的一条折线表示;西红柿的种植成本与上市时间的关系用图二的抛物线段表示.
(Ⅰ)写出图一表示的市场售价与时间的函数关系式p=f(t);写出图二表示的种植成本与时间的函数关系式Q=g(t);
(Ⅱ)认定市场售价减去种植成本为纯收益,问何时上市的西红柿纯收益最大?
(注:市场售价和种植成本的单位:元/102kg,时间单位:天)
解:(Ⅰ)由图一可得市场售价与时间的函数关系为
由图二可得种植成本与时间的函数关系为
g(t)= (t-150)2+100,0≤t≤300.
(Ⅱ)设t时刻的纯收益为h(t),则由题意得
h(t)=f(t)-g(t),
即
当0≤t≤200时,配方整理得
h(t)=-(t-50)2+100,
所以,当t=50时,h(t)取得区间[0,200]上的最大值100;
当200所以,当t=300时,h(t)取得区间(200,300]上的最大值87.5.
综上,由100>87.5可知,h(t)在区间[0,300]上可以取得最大值100,此时t=50,即从二月一日开始的第50天时,上市的西红柿纯收益最大
点评:本小题主要考查由函数图像建立函数关系式和求函数最大值的问题,考查运用所学知识解决实际问题的能力.
例2.某工厂第一季度某产品月生产量分别为1万件,1.2万件,1.3万件.为了估测以后每个月的产量,以这3个月的产量为依据,用一个函数模拟该产品的月产量y与月份x的关系.模拟函数可以选用二次函数或函数(其中a,b,c为常数).已知4月份的产量为1.36万件,问:用以上哪个函数作为模拟函数较好 为什么
分析:待定系数法求二次函数解析式.
解:设二次函数,由,,,解得:,,,.
由得,解得:,,,
即
又,,
,作为模拟函数更好.
点评:函数模型不确定,需要我们去探索,尝试,找到最合适的模型.本题给了两个函数模型供选择,如何选?结合条件中的数据进行处理.
例3.甲、乙两地相距S千米,汽车从甲地匀速行驶到乙地,速度不得超过c千米/时.已
知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度v
(千米/时)的平方成正比、比例系数为b;固定部分为a元.
(Ⅰ)把全程运输成本y(元)表示为速度v(千米/时)的函数,并指出这个函数的定义域;
(II)为了使全程运输成本最小,汽车应以多大速度行驶?
解:(Ⅰ)依题意知汽车从甲地匀速行驶到乙地所用时间为,全程运输成本为
故所求函数及其定义域为
(Ⅱ)依题意知S,a,b,v都为正数,故有
当且仅当.即时上式中等号成立
若,则当时,全程运输成本y最小,
若,则当时,有
=
因为c-v≥0,且a>bc2,故有a-bcv≥a-bc2>0,
所以,且仅当v=c时等号成立,
也即当v=c时,全程运输成本y最小.
综上知,为使全程运输成本y最小,当时行驶速度应为;当时行驶速度应为v=c.
点评:本小题主要考查建立函数关系、不等式性质、最大值、最小值等基础知识,考查综合应用所学数学知识、思想和方法解决实际问题的能力.
【反馈演练】
1.把长为12cm的细铁丝截成两段,各自围成一个正三角形,则这两个正三角形面积之和的最小值是___________.
2.某地高山上温度从山脚起每升高100m降低0.7℃,已知山顶的温度是14.1℃,山脚的温度是26℃,则此山的高度为_____17_____m.
3.为了稳定市场,确保农民增收,某农产品的市场收购价格与其前三个月的市场收购价格有关,且使与其前三个月的市场收购价格之差的平方和最小.若下表列出的是该产品前6个月的市场收购价格:
月份 1 2 3 4 5 6 7
价格(元/担) 68 78 67 71 72 70
则7月份该产品的市场收购价格应为______ 71_______元.
4.某公司在甲、乙两地销售一种品牌车,利润(单位:万元)分别为L1=5.06x-0.15 x 2和L2=2 x,其中x为销售量(单位:辆).若该公司在这两地共销售15辆车,则能获得的最大利润为____45.6___万元.
5.四位好朋友在一次聚会上,他们按照各自的爱好选择了形状不同、内空高度相等、杯口半径相等的圆口酒杯,如图所示.盛满酒后他们约定:先各自饮杯中酒的一半.设剩余酒的高度从左到右依次为,,,,则它们的大小关系正确的是( A )
A. B. C. D.
6.一根长为1的铁丝,分成两段分别围成一个正方形和一个圆,当正方形和圆的面积之和最小时,正方
形的周长为 .
7.建造一个容积为8m3 ,深为2m的长方体无盖水池.如果池底和池壁的造价每平方米分别为120元和80元,那么水池的最低总造价为_____1120____元.
8.为了预防流感,某学校对教室用药熏消毒法进行消毒. 已知药物释放过程中,
室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比;药物释放完毕后,
y与t的函数关系式为(a为常数),如图所示,根据图中提供的信息,
回答下列问题:
(Ⅰ)从药物释放开始,每立方米空气中的含药量y(毫克)与时间t(小时)
之间的函数关系式为.
(Ⅱ)据测定,当空气中每立方米的含药量降低到0.25毫克以下时,学生方可进教室,那从药物释放开始,至少需要经过 0.6 小时后,学生才能回到教室.
9.在经济学中,函数的边际函数定义为.某公司每月最多生产100台报警装置,生产x台的收入函数为(单位:元),其成本函数为(单位:元),利润是收入与成本之差.则利润函数的最大值为_____74120_____元,边际利润函数的最大值为____2440___元.
10.某单位用木料制作如图所示的框架,框架的下部是边长分别为x,y(单位:m)的矩形.上部是等腰直角三角形. 要求框架围成的总面积8cm2. 问x、y分别为多少时用料最省
解:由题意得 xy+x2=8,∴y==(0则框架用料长度为l=2x+2y+2()=(+)x+≥4.
当(+)x=,即x=8-4时等号成立.
此时,x=8-4,,
故当x为8-4m,y为m时,用料最省.
11.某厂生产某种零件,每个零件的成本为40元,出厂单价定为60元,该厂为鼓励销售商订购,决定当一次订购量超过100个时,每多订购一个,订购的全部零件的出厂单价就降低0.02元,但实际出厂单价不能低于51元.
(I)当一次订购量为多少个时,零件的实际出厂单价恰降为51元?
(II)设一次订购量为x个,零件的实际出厂单价为P元,写出函数的表达式;
(III)当销售商一次订购500个零件时,该厂获得的利润是多少元?如果订购1000个,利润又是多少元?(工厂售出一个零件的利润=实际出厂单价-成本)
解:(I)设每个零件的实际出厂价恰好降为51元时,一次订购量为个,则
因此,当一次订购量为550个时,每个零件的实际出厂价恰好降为51元
(II)当时,
当时,
当时,
所以
(III)设销售商的一次订购量为x个时,工厂获得的利润为L元,则
当时,;当时,
因此,当销售商一次订购500个零件时,该厂获得的利润是6000元;
如果订购1000个,利润是11000元.
12.设计一幅宣传画,要求画面面积为4840cm2,画面的宽与高的比为(<1),画面的上、下各留8cm空白,左、右各留5cm空白.
(1)怎样确定画面的高与宽尺寸,能使宣传画所用纸张面积最小?
(2)如果要求,那么为何值时,能使宣传画所用纸张面积最小
解:(1)设画面高为x cm,宽为x cm,则x2 = 4840.
设纸张面积为S,有S = (x+16) (x+10)= x2+(16+10) x+160,
将代入上式,得.
当时,即时,S取得最小值.
此时,高:,宽:.
(2)如果,可设,则由的表达式得
44=
由于,故
因此,所以在区间[]内单调递增.
从而,对于,当=时,取得最小值
答:画面高为88cm,宽为55cm时,能使所用纸张面积最小.如果要求,当=时,所用纸张面积最小.
第3题
第8题
第10题
x
y
【考点导读】
1.能根据实际问题的情境建立函数模型,结合对函数性质的研究,给出问题的解答.
2.理解数据拟合是用来对事物的发展规律进行估计的一种方法,会根据条件借助计算工具解决一些简单的实际问题.
3.培养学生数学地分析问题,探索问题,解决问题的能力.
【基础练习】
1.2006年11月15日起,国内投寄首重100g以内的外部信函的邮资标准:每封信不超过20g时付邮资120分,超过20g而不超过40g付邮资240分,超过40g而不超过60g付邮资360分,依次类推.如果某人所寄一封信的质量为82.5g,那么他应付邮资为____600___分.
2.今有一组实验数据如下:
1.99 3.0 4.0 5.1 6.12
1.5 4.04 7.5 12 18.01
现准备用下列函数中的一个近似地表示这些数据满足的规律,
① ② ③ ④
其中最接近的一个的序号是______③_______.
3.以墙为一边,用篱笆围成长方形的场地,并用平行于一边的篱笆隔开(如图),已知篱笆的总长为定值l,
则这块场地的最大面积是___________.
4.某种放射性物质不断变化为其他物质,每经过1年,这种物质剩留的质量是原来的84%,则这种物质的
剩留量关于时间的函数关系式为_______________.
5.某摩托车生产企业,上年度生产摩托车的投入成本为1万元/辆,出厂价为1.2万元/辆,年销售量为1000辆.本年度为适应市场需求,计划提高产品档次,适度增加投入成本.若每辆车投入成本增加的比例为x(0 < x < 1),则出厂价相应的提高比例为0.75x,同时预计年销售量增加的比例为0.6x.已知年利润 = (出厂价-投入成本)×年销售量.
(Ⅰ)写出本年度预计的年利润y与投入成本增加的比例x的关系式;
(Ⅱ)为使本年度的年利润比上年有所增加,问投入成本增加的比例x应在什么范围内?
解:(Ⅰ)由题意得y = [ 1.2×(1+0.75x)-1×(1 + x) ] ×1000×( 1+0.6x )(0 < x < 1)
整理得 y = -60x2 + 20x + 200(0 < x < 1).
(Ⅱ)要保证本年度的利润比上年度有所增加,当且仅当
即 解不等式得.
答:为保证本年度的年利润比上年度有所增加,投入成本增加的比例x应满足0 < x < 0.33.
【范例解析】
例1.某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的300天内,西红柿市场售价与上市时间的关系用图一的一条折线表示;西红柿的种植成本与上市时间的关系用图二的抛物线段表示.
(Ⅰ)写出图一表示的市场售价与时间的函数关系式p=f(t);写出图二表示的种植成本与时间的函数关系式Q=g(t);
(Ⅱ)认定市场售价减去种植成本为纯收益,问何时上市的西红柿纯收益最大?
(注:市场售价和种植成本的单位:元/102kg,时间单位:天)
解:(Ⅰ)由图一可得市场售价与时间的函数关系为
由图二可得种植成本与时间的函数关系为
g(t)= (t-150)2+100,0≤t≤300.
(Ⅱ)设t时刻的纯收益为h(t),则由题意得
h(t)=f(t)-g(t),
即
当0≤t≤200时,配方整理得
h(t)=-(t-50)2+100,
所以,当t=50时,h(t)取得区间[0,200]上的最大值100;
当200
综上,由100>87.5可知,h(t)在区间[0,300]上可以取得最大值100,此时t=50,即从二月一日开始的第50天时,上市的西红柿纯收益最大
点评:本小题主要考查由函数图像建立函数关系式和求函数最大值的问题,考查运用所学知识解决实际问题的能力.
例2.某工厂第一季度某产品月生产量分别为1万件,1.2万件,1.3万件.为了估测以后每个月的产量,以这3个月的产量为依据,用一个函数模拟该产品的月产量y与月份x的关系.模拟函数可以选用二次函数或函数(其中a,b,c为常数).已知4月份的产量为1.36万件,问:用以上哪个函数作为模拟函数较好 为什么
分析:待定系数法求二次函数解析式.
解:设二次函数,由,,,解得:,,,.
由得,解得:,,,
即
又,,
,作为模拟函数更好.
点评:函数模型不确定,需要我们去探索,尝试,找到最合适的模型.本题给了两个函数模型供选择,如何选?结合条件中的数据进行处理.
例3.甲、乙两地相距S千米,汽车从甲地匀速行驶到乙地,速度不得超过c千米/时.已
知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度v
(千米/时)的平方成正比、比例系数为b;固定部分为a元.
(Ⅰ)把全程运输成本y(元)表示为速度v(千米/时)的函数,并指出这个函数的定义域;
(II)为了使全程运输成本最小,汽车应以多大速度行驶?
解:(Ⅰ)依题意知汽车从甲地匀速行驶到乙地所用时间为,全程运输成本为
故所求函数及其定义域为
(Ⅱ)依题意知S,a,b,v都为正数,故有
当且仅当.即时上式中等号成立
若,则当时,全程运输成本y最小,
若,则当时,有
=
因为c-v≥0,且a>bc2,故有a-bcv≥a-bc2>0,
所以,且仅当v=c时等号成立,
也即当v=c时,全程运输成本y最小.
综上知,为使全程运输成本y最小,当时行驶速度应为;当时行驶速度应为v=c.
点评:本小题主要考查建立函数关系、不等式性质、最大值、最小值等基础知识,考查综合应用所学数学知识、思想和方法解决实际问题的能力.
【反馈演练】
1.把长为12cm的细铁丝截成两段,各自围成一个正三角形,则这两个正三角形面积之和的最小值是___________.
2.某地高山上温度从山脚起每升高100m降低0.7℃,已知山顶的温度是14.1℃,山脚的温度是26℃,则此山的高度为_____17_____m.
3.为了稳定市场,确保农民增收,某农产品的市场收购价格与其前三个月的市场收购价格有关,且使与其前三个月的市场收购价格之差的平方和最小.若下表列出的是该产品前6个月的市场收购价格:
月份 1 2 3 4 5 6 7
价格(元/担) 68 78 67 71 72 70
则7月份该产品的市场收购价格应为______ 71_______元.
4.某公司在甲、乙两地销售一种品牌车,利润(单位:万元)分别为L1=5.06x-0.15 x 2和L2=2 x,其中x为销售量(单位:辆).若该公司在这两地共销售15辆车,则能获得的最大利润为____45.6___万元.
5.四位好朋友在一次聚会上,他们按照各自的爱好选择了形状不同、内空高度相等、杯口半径相等的圆口酒杯,如图所示.盛满酒后他们约定:先各自饮杯中酒的一半.设剩余酒的高度从左到右依次为,,,,则它们的大小关系正确的是( A )
A. B. C. D.
6.一根长为1的铁丝,分成两段分别围成一个正方形和一个圆,当正方形和圆的面积之和最小时,正方
形的周长为 .
7.建造一个容积为8m3 ,深为2m的长方体无盖水池.如果池底和池壁的造价每平方米分别为120元和80元,那么水池的最低总造价为_____1120____元.
8.为了预防流感,某学校对教室用药熏消毒法进行消毒. 已知药物释放过程中,
室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比;药物释放完毕后,
y与t的函数关系式为(a为常数),如图所示,根据图中提供的信息,
回答下列问题:
(Ⅰ)从药物释放开始,每立方米空气中的含药量y(毫克)与时间t(小时)
之间的函数关系式为.
(Ⅱ)据测定,当空气中每立方米的含药量降低到0.25毫克以下时,学生方可进教室,那从药物释放开始,至少需要经过 0.6 小时后,学生才能回到教室.
9.在经济学中,函数的边际函数定义为.某公司每月最多生产100台报警装置,生产x台的收入函数为(单位:元),其成本函数为(单位:元),利润是收入与成本之差.则利润函数的最大值为_____74120_____元,边际利润函数的最大值为____2440___元.
10.某单位用木料制作如图所示的框架,框架的下部是边长分别为x,y(单位:m)的矩形.上部是等腰直角三角形. 要求框架围成的总面积8cm2. 问x、y分别为多少时用料最省
解:由题意得 xy+x2=8,∴y==(0
当(+)x=,即x=8-4时等号成立.
此时,x=8-4,,
故当x为8-4m,y为m时,用料最省.
11.某厂生产某种零件,每个零件的成本为40元,出厂单价定为60元,该厂为鼓励销售商订购,决定当一次订购量超过100个时,每多订购一个,订购的全部零件的出厂单价就降低0.02元,但实际出厂单价不能低于51元.
(I)当一次订购量为多少个时,零件的实际出厂单价恰降为51元?
(II)设一次订购量为x个,零件的实际出厂单价为P元,写出函数的表达式;
(III)当销售商一次订购500个零件时,该厂获得的利润是多少元?如果订购1000个,利润又是多少元?(工厂售出一个零件的利润=实际出厂单价-成本)
解:(I)设每个零件的实际出厂价恰好降为51元时,一次订购量为个,则
因此,当一次订购量为550个时,每个零件的实际出厂价恰好降为51元
(II)当时,
当时,
当时,
所以
(III)设销售商的一次订购量为x个时,工厂获得的利润为L元,则
当时,;当时,
因此,当销售商一次订购500个零件时,该厂获得的利润是6000元;
如果订购1000个,利润是11000元.
12.设计一幅宣传画,要求画面面积为4840cm2,画面的宽与高的比为(<1),画面的上、下各留8cm空白,左、右各留5cm空白.
(1)怎样确定画面的高与宽尺寸,能使宣传画所用纸张面积最小?
(2)如果要求,那么为何值时,能使宣传画所用纸张面积最小
解:(1)设画面高为x cm,宽为x cm,则x2 = 4840.
设纸张面积为S,有S = (x+16) (x+10)= x2+(16+10) x+160,
将代入上式,得.
当时,即时,S取得最小值.
此时,高:,宽:.
(2)如果,可设,则由的表达式得
44=
由于,故
因此,所以在区间[]内单调递增.
从而,对于,当=时,取得最小值
答:画面高为88cm,宽为55cm时,能使所用纸张面积最小.如果要求,当=时,所用纸张面积最小.
第3题
第8题
第10题
x
y
同课章节目录
