分式的通分
图片预览






文档简介
(共18张PPT)
教学目标
1.理解分式通分的概念;
2.会用分式的基本性质进行分式通分分。
重点:分式的通分.
难点:分式的分母是多项式的通分.
(1)类比分数的通分;(2)熟练地进行因式分解
突破难点的方法:
教学重点、难点
第3课时 16.1.2 分式的约分
1.分式的基本性质:
一个分式的分子与分母同乘(或除以)
一个 ,分式的值___________
,
不变
(一)复习回顾
不为0的整式
2.什么叫约分?把一个分式的分子和分母的公因式约去,不改变分式的值,这种变形叫做分式的约分。
约分:
1.分数的通分:
(二)问题情景
什么叫做分数的通分?
1. 通分:
最简公分母:
4×3×2=24
(二)问题情景
问题 类比分数的通分你能把下列分式化为分母相同的分式吗?
(二)问题情景
(1)引出分式通分的概念:P7
(2)如何进行分式通分?
把各分式化成相同
分母的分式叫做
分式的通分.
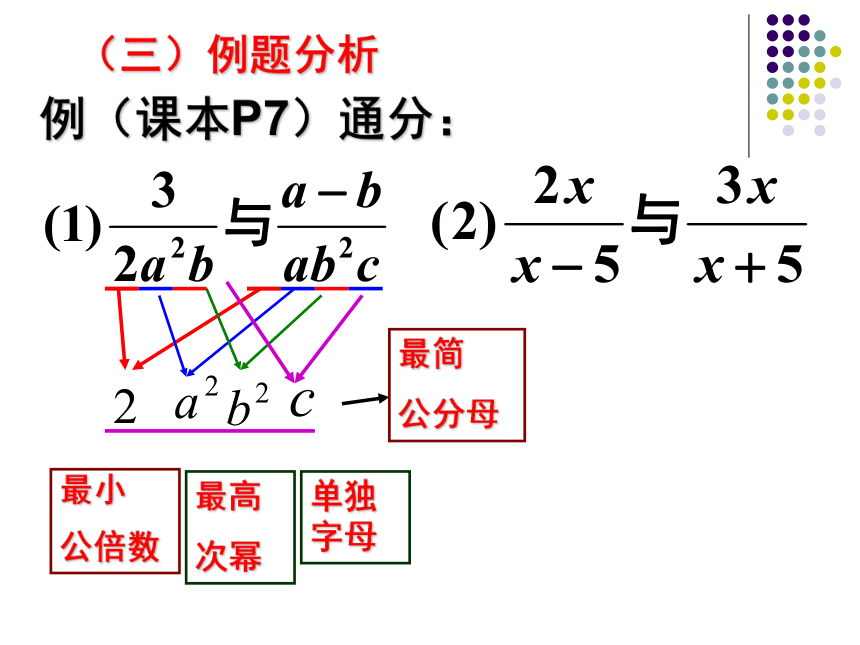
(三)例题分析
例(课本P7)通分:
最小
公倍数
最简
公分母
最高
次幂
单独字母
最简
公分母
不同的因式
最简
公分母
(三)例题分析
例1.(课本P7)通分:
解:
最简公分母是
例1.(课本P7)通分:
解:
最简公分母是
例1.(课本P7)通分:
1.怎样找公分母?
2.找最简公分母应从方面考虑?
第一要看系数;第二要看字母
通分要先确定分式的最简公分母。
方法归纳
通分:
最简公分母
一般取各分母的所有因式的最高次幂的积作公分母,它叫做最简公分母。
3. 三个分式 的最简公分母 是
1.三个分式
的最简公分母是( )
B.
C.
D.
2.分式
的最简公分母是_________.
A.
(四)课堂练习(补充)
(2)
(1)
(2)
(1)
1.(课本P8)通分:
(四)课堂练习
2.(补充)通分:
例2(补充)通分
(五)补充例题
(六)知识梳理
1、把各分式化成相同分母的分式叫做
分式的通分.
2、一般取各分母的所有因式的最高次幂
的积作公分母,它叫做最简公分母。
(七)课后作业
课本P9 第7题
教学目标
1.理解分式通分的概念;
2.会用分式的基本性质进行分式通分分。
重点:分式的通分.
难点:分式的分母是多项式的通分.
(1)类比分数的通分;(2)熟练地进行因式分解
突破难点的方法:
教学重点、难点
第3课时 16.1.2 分式的约分
1.分式的基本性质:
一个分式的分子与分母同乘(或除以)
一个 ,分式的值___________
,
不变
(一)复习回顾
不为0的整式
2.什么叫约分?把一个分式的分子和分母的公因式约去,不改变分式的值,这种变形叫做分式的约分。
约分:
1.分数的通分:
(二)问题情景
什么叫做分数的通分?
1. 通分:
最简公分母:
4×3×2=24
(二)问题情景
问题 类比分数的通分你能把下列分式化为分母相同的分式吗?
(二)问题情景
(1)引出分式通分的概念:P7
(2)如何进行分式通分?
把各分式化成相同
分母的分式叫做
分式的通分.
(三)例题分析
例(课本P7)通分:
最小
公倍数
最简
公分母
最高
次幂
单独字母
最简
公分母
不同的因式
最简
公分母
(三)例题分析
例1.(课本P7)通分:
解:
最简公分母是
例1.(课本P7)通分:
解:
最简公分母是
例1.(课本P7)通分:
1.怎样找公分母?
2.找最简公分母应从方面考虑?
第一要看系数;第二要看字母
通分要先确定分式的最简公分母。
方法归纳
通分:
最简公分母
一般取各分母的所有因式的最高次幂的积作公分母,它叫做最简公分母。
3. 三个分式 的最简公分母 是
1.三个分式
的最简公分母是( )
B.
C.
D.
2.分式
的最简公分母是_________.
A.
(四)课堂练习(补充)
(2)
(1)
(2)
(1)
1.(课本P8)通分:
(四)课堂练习
2.(补充)通分:
例2(补充)通分
(五)补充例题
(六)知识梳理
1、把各分式化成相同分母的分式叫做
分式的通分.
2、一般取各分母的所有因式的最高次幂
的积作公分母,它叫做最简公分母。
(七)课后作业
课本P9 第7题
