28.5《弧长和扇形面积》课时练习(Word版 含答案)2021-2022学年九年级数学冀教版上册
文档属性
| 名称 | 28.5《弧长和扇形面积》课时练习(Word版 含答案)2021-2022学年九年级数学冀教版上册 |  | |
| 格式 | doc | ||
| 文件大小 | 146.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-19 19:51:22 | ||
图片预览


文档简介
冀教版数学九年级上册
28.5《弧长和扇形面积》课时练习
一、选择题
1.有一条弧的长为2πcm,半径为2cm,则这条弧所对的圆心角的度数是(
)
A.90°
B.120°
C.180°
D.135°
2.若扇形的圆心角为90°,半径为6,则该扇形的弧长为( )
A.π??
?
B.2π??
???
C.3π??
??
D.6π
3.若扇形的半径为6,圆心角为120°,则此扇形的弧长是( )
A.3π
B.4π
C.5π
D.6π
4.如图,从一张腰长为60cm,顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD,用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的高为(
)
A.10cm
B.15cm
C.10cm
D.20cm
5.如图,圆锥底面半径为rcm,母线长为10cm,其侧面展开图是圆心角为216°的扇形,则r的值为(
)
A.3
B.6
C.3π
D.6π
6.如图,线段AB经过⊙O的圆心,AC,BD分别与⊙O相切于点C,D.若AC=BD=4,∠A=45°,则的长度为( )
A.π???
??
B.2π????
?
C.2π???
??
D.4π
7.如图,在半径为6的⊙O中,点A,B,C都在⊙O上,四边形OABC是平行四边形,则图中阴影部分的面积为( )
A.6π??
?
B.3π???
?
C.2π???
?
D.2π
8.将一盛有不足半杯水的圆柱形玻璃水杯拧紧杯盖后放倒,水平放置在桌面上,水杯的底面如图所示,已知水杯内径(图中小圆的直径)是8cm,水的最大深度是2cm,则杯底有水部分的面积是(
)
A.(π﹣4)cm2
B.(π﹣8)cm2
C.(π﹣4)cm2
D.(π﹣2)cm2
二、填空题
9.已知扇形的圆心角为45°,半径长为12,则该扇形的弧长为
.
10.扇形的圆心角为120°,弧长为6πcm,那么这个扇形的面积为
cm2.
11.若一个圆锥的底面半径为2,母线长为6,则该圆锥侧面展开图的圆心角是
°.
12.已知扇形的圆心角为150°,它所对应的弧长20πcm,则此扇形的半径是??
??cm,面积是???cm2.
13.已知半径为2cm的扇形,其弧长为,则这个扇形的面积是_________.
14.如图,⊙O的半径为2,点A,B在⊙O上,∠AOB=90°,则阴影部分面积为_______.
三、解答题
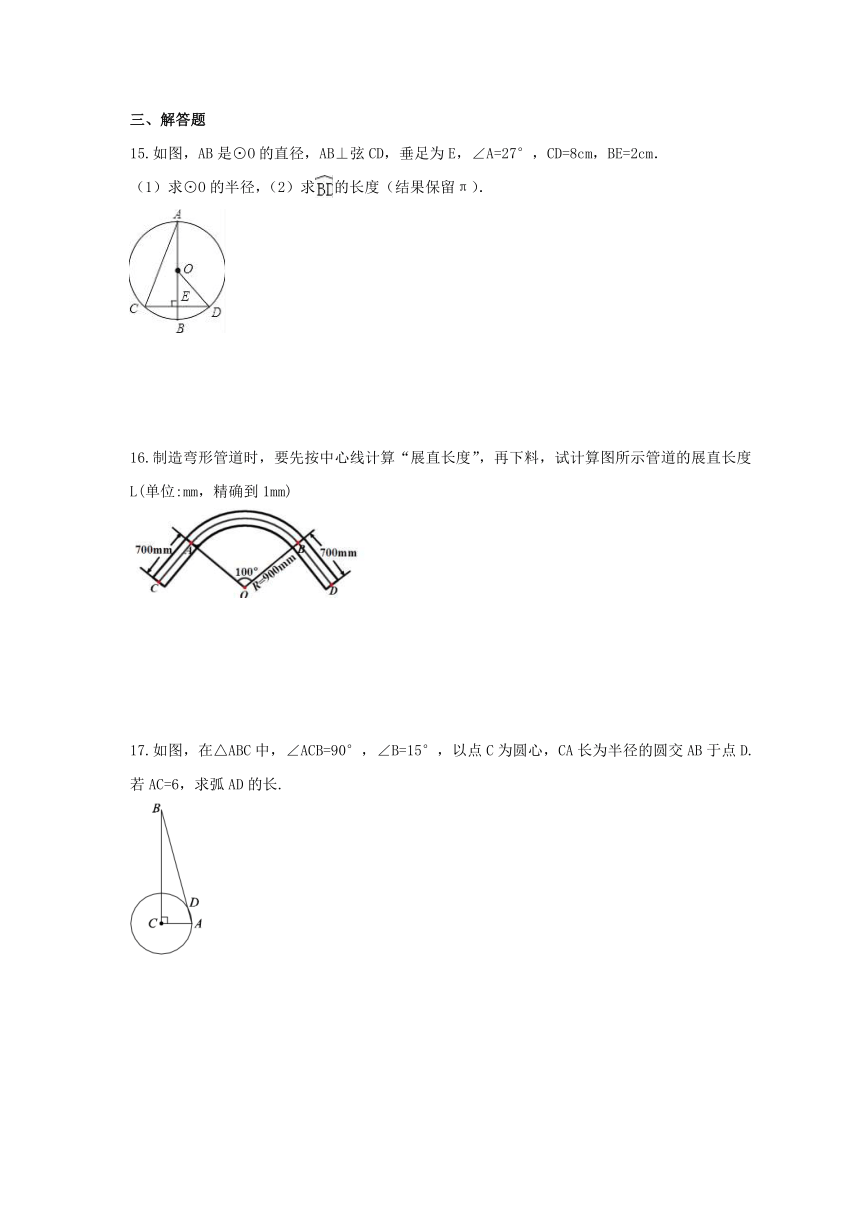
15.如图,AB是⊙O的直径,AB⊥弦CD,垂足为E,∠A=27°,CD=8cm,BE=2cm.
(1)求⊙O的半径,(2)求的长度(结果保留π).
16.制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算图所示管道的展直长度L(单位:mm,精确到1mm)
17.如图,在△ABC中,∠ACB=90°,∠B=15°,以点C为圆心,CA长为半径的圆交AB于点D.若AC=6,求弧AD的长.
18.如图,在平面直角坐标系中,等腰Rt△OAB斜边OB在y轴上,且OB=4.
(1)画出△OAB绕原点O顺时针旋转90°后得到的三角形;
(2)求线段OB在上述旋转过程中所扫过部分图形的面积(即旋转前后OB与点B轨迹所围成的封闭图形的面积).
参考答案
1.答案为:C;
2.答案为:C.
3.答案为:B
4.答案为:D
5.答案为:A
6.答案为:B.
7.答案为:A.
8.答案为:A
9.答案为:3π.
10.答案为:6π×9÷2=27πcm2.
11.答案为120.
12.答案为:24;240π;????
13.答案为:cm2
14.答案为:π-2
15.解:连接OC,如图所示:
∵AB是⊙O的直径,弦CD⊥AB,∴CE=DE=CD=4cm,
∵BE=2cm,∴OE=OC﹣2,∴OC2=42+(OC﹣2)2,
∴OC=∴△COE为等腰直角三角形,∴OC=5,即⊙O的半径为5cm;
(2)∵∠A=27°,∴∠BOC=54°,∴的长度==π,
∵,∴的长度=π.
16.解:L=2×700+=500π+1400≈2970mm.
17.解:连接CD.
∵AC=CD,∴∠CAD=∠CDA.
∵∠ACB=90°,∠B=15°,∴∠CAD=75°,
∴∠ACD=30°.
∵AC=6,∴的长度为=π.
18.解:(1)画图正确(如图);
(2)所扫过部分图形是扇形,它的面积是:π×42=4π.
28.5《弧长和扇形面积》课时练习
一、选择题
1.有一条弧的长为2πcm,半径为2cm,则这条弧所对的圆心角的度数是(
)
A.90°
B.120°
C.180°
D.135°
2.若扇形的圆心角为90°,半径为6,则该扇形的弧长为( )
A.π??
?
B.2π??
???
C.3π??
??
D.6π
3.若扇形的半径为6,圆心角为120°,则此扇形的弧长是( )
A.3π
B.4π
C.5π
D.6π
4.如图,从一张腰长为60cm,顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD,用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的高为(
)
A.10cm
B.15cm
C.10cm
D.20cm
5.如图,圆锥底面半径为rcm,母线长为10cm,其侧面展开图是圆心角为216°的扇形,则r的值为(
)
A.3
B.6
C.3π
D.6π
6.如图,线段AB经过⊙O的圆心,AC,BD分别与⊙O相切于点C,D.若AC=BD=4,∠A=45°,则的长度为( )
A.π???
??
B.2π????
?
C.2π???
??
D.4π
7.如图,在半径为6的⊙O中,点A,B,C都在⊙O上,四边形OABC是平行四边形,则图中阴影部分的面积为( )
A.6π??
?
B.3π???
?
C.2π???
?
D.2π
8.将一盛有不足半杯水的圆柱形玻璃水杯拧紧杯盖后放倒,水平放置在桌面上,水杯的底面如图所示,已知水杯内径(图中小圆的直径)是8cm,水的最大深度是2cm,则杯底有水部分的面积是(
)
A.(π﹣4)cm2
B.(π﹣8)cm2
C.(π﹣4)cm2
D.(π﹣2)cm2
二、填空题
9.已知扇形的圆心角为45°,半径长为12,则该扇形的弧长为
.
10.扇形的圆心角为120°,弧长为6πcm,那么这个扇形的面积为
cm2.
11.若一个圆锥的底面半径为2,母线长为6,则该圆锥侧面展开图的圆心角是
°.
12.已知扇形的圆心角为150°,它所对应的弧长20πcm,则此扇形的半径是??
??cm,面积是???cm2.
13.已知半径为2cm的扇形,其弧长为,则这个扇形的面积是_________.
14.如图,⊙O的半径为2,点A,B在⊙O上,∠AOB=90°,则阴影部分面积为_______.
三、解答题
15.如图,AB是⊙O的直径,AB⊥弦CD,垂足为E,∠A=27°,CD=8cm,BE=2cm.
(1)求⊙O的半径,(2)求的长度(结果保留π).
16.制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算图所示管道的展直长度L(单位:mm,精确到1mm)
17.如图,在△ABC中,∠ACB=90°,∠B=15°,以点C为圆心,CA长为半径的圆交AB于点D.若AC=6,求弧AD的长.
18.如图,在平面直角坐标系中,等腰Rt△OAB斜边OB在y轴上,且OB=4.
(1)画出△OAB绕原点O顺时针旋转90°后得到的三角形;
(2)求线段OB在上述旋转过程中所扫过部分图形的面积(即旋转前后OB与点B轨迹所围成的封闭图形的面积).
参考答案
1.答案为:C;
2.答案为:C.
3.答案为:B
4.答案为:D
5.答案为:A
6.答案为:B.
7.答案为:A.
8.答案为:A
9.答案为:3π.
10.答案为:6π×9÷2=27πcm2.
11.答案为120.
12.答案为:24;240π;????
13.答案为:cm2
14.答案为:π-2
15.解:连接OC,如图所示:
∵AB是⊙O的直径,弦CD⊥AB,∴CE=DE=CD=4cm,
∵BE=2cm,∴OE=OC﹣2,∴OC2=42+(OC﹣2)2,
∴OC=∴△COE为等腰直角三角形,∴OC=5,即⊙O的半径为5cm;
(2)∵∠A=27°,∴∠BOC=54°,∴的长度==π,
∵,∴的长度=π.
16.解:L=2×700+=500π+1400≈2970mm.
17.解:连接CD.
∵AC=CD,∴∠CAD=∠CDA.
∵∠ACB=90°,∠B=15°,∴∠CAD=75°,
∴∠ACD=30°.
∵AC=6,∴的长度为=π.
18.解:(1)画图正确(如图);
(2)所扫过部分图形是扇形,它的面积是:π×42=4π.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
