2021-2022学年北师大版九年级数学上册2.6应用一元二次方程同步优生辅导训练(Word版,附答案解析)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学上册2.6应用一元二次方程同步优生辅导训练(Word版,附答案解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 94.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-19 00:00:00 | ||
图片预览



文档简介
2021-2022学年北师大版九年级数学上册《2.6应用一元二次方程》
同步优生辅导训练(附答案)
1.“古越龙山”酿酒公司由于注重对市场调研和新产品的研发,新研制的某款瓶装酒获得市场的认可,今年四月份销售了50万瓶,按市场供需趋势预计今年二季度可销售182万瓶.设该款酒的销售量今年五、六月份平均每月的增长率为x,那么x满足的方程是( )
A.50(1+x)2=182
B.50+50(1+x)+50(1+x)2=182
C.50(1+2x)=182
D.50+50(1+x)+50(1+2x)2=182
2.某校初一年级开展了一班一特色活动,2001班以“地”为特色在学校的试验园地进行种植蔬菜活动.试验园的形状是长15米、宽8米的矩形,为便于管理,要在中间开辟一横两纵共三条等宽的小道,使种植面积为110平方米,则小道的宽为多少米?若设小道的宽为x米,则根据题意,列方程为( )
A.(15+2x)(8+x)=110
B.(15﹣2x)(8﹣x)=110
C.(15+x)(8+2x)=110
D.(15﹣x)(8﹣2x)=110
3.已知有1人患了某新型肺炎,经过两轮传染后共有256人患病,设每轮传染中平均一人传染x人,则可以列方程( )
A.1+2x=256
B.1+x2=256
C.(1+x)2=256
D.1+x=256
4.《九章算术》是我国古代数学的经典著作,它的出现标志着中国古代数学形成了完整的体系,其“勾股”章中记载了一个数学问题:“今有户高多于广六尺,两隅相去适一丈,问户高、广各几何?”译文为:“已知有一扇矩形门的高比宽多6尺,门的对角线长为1丈(1丈=10尺),那么门的高和宽各是多少?”如果设门的宽为x尺,则可列方程为( )
A.x2+(x+6)2=102
B.x2+(x+6)2=12
C.x2+(x﹣6)2=102
D.x2+(x﹣6)2=12
5.某小区花园有一块长方形花圃,它的宽为5m,若长边不变,将短边扩大,使得扩大后的花圃形状为正方形,且面积比原来增加15m2,设原来花圃长边为xm,可列方程( )
A.x?+5x=15
B.x2﹣5x=15
C.(x﹣5)2=15
D.x﹣25=15
6.元旦来临前,某商场将一件原价为a元的衬衫以一个给定的百分比提升价格,元旦那天商场又按照新的价格以相同的百分比降低了这件衬衫的价格,最终,衬衫的价格比原价降低了0.16a元,则这个给定的百分比为( )
A.16%
B.36%
C.40%
D.50%
7.某工厂2021年数字化改造总投入100万元,2023年总投入预计达到180万元,设年平均增长率为x,则可列方程为( )
A.100(1+x)=180
B.100(1+2x)=180
C.100(1+x+x2)=180
D.100(1+x)2=180
8.欧几里得在《几何原本》中,记载了用图解法解方程x2+ax=b2的方法,类似地我们可以用折纸的方法求方程x2+x﹣1=0的一个正根.如图,一张边长为1的正方形的纸片ABCD,先折出AD、BC的中点G、H,再折出线段AN,然后通过沿线段AN折叠使AD落在线段AH上,得到点D的新位置P,并连接NP、NH,此时,在下列四个选项中,有一条线段的长度恰好是方程x2+x﹣1=0的一个正根,则这条线段是( )
A.线段BH
B.线段DN
C.线段CN
D.线段NH
9.某校八年级组织篮球赛,若每两班之间赛一场,共进行了28场,则该校八年级有
个班级.
10.两个相邻偶数的积是168,则这两个相邻偶数中较大的数是
.
11.哈尔滨市某楼盘以每平方米10000元的均价对外销售,经过连续两次降价后,均价为每平方米8100元,则平均每次降价的百分率为
.
12.如图是一块矩形铁皮,将四个角各剪去一个边长为2米的正方形后剩下的部分做成一个容积为96立方米的无盖长方体箱子,已知长方体箱子底面的长比宽多2米,则矩形铁皮的面积为
平方米.
13.商场某种商品进价为120元/件,售价130元/件时,每天可销售70件;售价单价高于130元时,每涨价1元,日销售量就减少1件.据此,若销售单价为
元时,商场每天盈利达1500元.
14.中国古代数学家杨辉的《田亩比类乘除捷法》中记载:“直田积八百六十四步,只云阔不及长一十二步,问阔及长各几步?翻译成数学问题是:一块矩形田地的面积为864平方步,它的宽比长少12步,问它的长与宽各多少步?利用方程思想,设宽为x步,则依题意列方程为
.
15.已知3个连续整数的和为m,它们的平方和是n,且n=11(m﹣8),则m=
.
16.在研究:“任意给定一个矩形A,是否存在另一个矩形B,它的周长和面积分别是已知矩形周长和面积的一半”时,小明发现:当已知矩形A的长和宽分别为6和1时,存在一个矩形B的周长和面积分别是矩形A周长和面积的一半,那么矩形B的长为
.
17.2020年突如其来的新型冠状病毒疫情,给生鲜电商带来了意想不到的流量和机遇,据统计某生鲜电商平台1月份的销售额是1440万元,3月份的销售额是2250万元.
(1)若该平台1月份到3月份的月平均增长率都相同,求月平均增长率是多少?
(2)市场调查发现,某水果在“盒马鲜生”平台上的售价为20元/千克时,每天能销售200千克,售价每降价2元,每天可多售出100千克,为了推广宣传,商家决定降价促销,同时尽量减少库存,已知该水果的成本价为12元/千克,若使销售该水果每天获利1750元,则售价应降低多少元?
18.某商店以每件40元的价格进了一批热销商品,出售价格经过两个月的调整,从每件50元上涨到每件72元,此时每月可售出188件商品.
(1)求该商品平均每月的价格增长率;
(2)因某些原因,商家需尽快将这批商品售出,决定降价出售.经过市场调查发现:售价每下降一元,每个月多卖出一件,设实际售价为x元,则x为多少元时商品每月的利润可达到4000元.
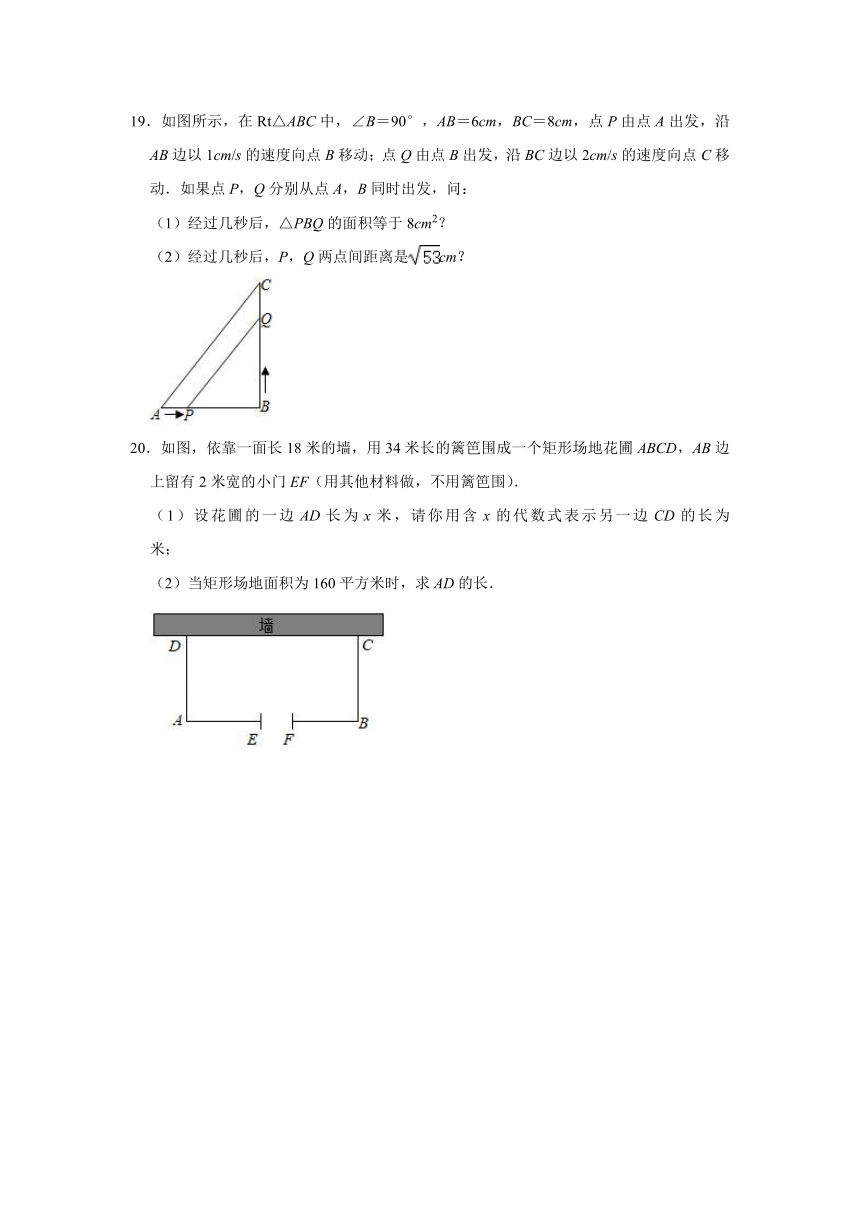
19.如图所示,在Rt△ABC中,∠B=90°,AB=6cm,BC=8cm,点P由点A出发,沿AB边以1cm/s的速度向点B移动;点Q由点B出发,沿BC边以2cm/s的速度向点C移动.如果点P,Q分别从点A,B同时出发,问:
(1)经过几秒后,△PBQ的面积等于8cm2?
(2)经过几秒后,P,Q两点间距离是cm?
20.如图,依靠一面长18米的墙,用34米长的篱笆围成一个矩形场地花圃ABCD,AB边上留有2米宽的小门EF(用其他材料做,不用篱笆围).
(1)设花圃的一边AD长为x米,请你用含x的代数式表示另一边CD的长为
米;
(2)当矩形场地面积为160平方米时,求AD的长.
参考答案
1.解:依题意得五、六月份的销量产量为50(1+x)、50(1+x)2,
∴50+50(1+x)+50(1+x)2=182.
故选:B.
2.解:设小道的宽为x米,则6个小矩形可合成长为(15﹣2x)米、宽为(8﹣x)米的大矩形,
依题意得:(15﹣2x)(8﹣x)=110.
故选:B.
3.解:设每轮传染中平均一个人传染了x个人,
第一轮传染后患流感的人数是:1+x,
第二轮传染后患流感的人数是:1+x+x(1+x),
而已知经过两轮传染后共有256人患了流感,则可得方程,
1+x+x(1+x)=256,即(1+x)2=256.
故选:C.
4.解:设门的宽为x尺,那么这个门的高为(x+6)尺,根据题意得方程:
x2+(x+6)2=102,
故选:A.
5.解:设原来绿地的长边为x(m),根据题意得
x2﹣5x=15,
故选:B.
6.解:设这个给定的百分比为x,根据题意得,
a(1+x)(1﹣x)=a﹣0.16a,
解得x1=0.4,x2=﹣0.4(舍去),
即这个给定的百分比为40%.
故选:C.
7.解:设年平均增长率为x,则2022的数字化改造总投入为:100(1+x)万元,2023的数字化改造总投入为:100(1+x)2万元,那么可得方程:100(1+x)2=180.
故选:D.
8.解:设DN=m,则NC=1﹣m.
由题意可知:△ADN≌△APN,H是BC的中点,
∴DN=NP=m,CH=0.5.
∵S正方形=S△ABH+S△ADN+S△CHN+SANH,
∴1×1=×1×+×1×m+××(1﹣m)+××m,
∴m=.
∵x2+x﹣1=0的解为:x=﹣±,
∴取正值为x=.
∴这条线段是线段DN.
故选:B.
9.解:设八年级有x个班,
依题意得:x(x﹣1)=28,
整理得:x2﹣x﹣56=0,
解得:x1=8,x2=﹣7(不合题意,舍去).
则该校八年级有8个班级.
故答案为:8.
10.解:设这两个相邻偶数中较大的数是x,则另外一个偶数为(x﹣2),
依题意得:x(x﹣2)=168,
整理得:x?﹣2x﹣168=0,
解得:x1=14,x2=﹣12.
故答案为:14或﹣12.
11.解:设平均每次降价的百分率为x,
依题意得:10000(1﹣x)2=8100,
解得:x1=0.1=10%,x2=1.9(不合题意,舍去).
故答案为:10%.
12.解:设矩形铁皮的宽为x米,则长为(x+2)米,
依题意得:(x+2﹣2×2)(x﹣2×2)×2=96,
整理得:x2﹣6x﹣40=0,
解得:x1=﹣4(不合题意,舍去),x2=10,
∴(x+2)x=(10+2)×10=120(平方米).
故答案为:120.
13.解:设销售单价为x元,则每天可销售70﹣(x﹣130)=(200﹣x)件,
依题意得:(x﹣120)(200﹣x)=1500,
整理得:x2﹣320x+25500=0,
解得:x1=150,x2=170.
故答案为:150或170.
14.解:∵矩形的宽为x(步),且宽比长少12(步),
∴矩形的长为(x+12)(步).
依题意,得:x(x+12)=864.
故答案为:x(x+12)=864.
15.解:设三个整数分别为a,a+1,a+2,
所以
m=3a+3,n=a2+(a+1)2+(a+2)2=3a2+6a+5,
由n=11(m﹣8),
所以
3a2+6a+5=11(3a﹣5),
解得a=4或5,
则m=15或18.
16.解:由已知可得,
矩形A的周长是(6+1)×2=14,面积是6×1=6,
则矩形B的周长是7,面积是3,
设矩形B的长为x,则宽为3.5﹣x,
则x(3.5﹣x)=3,
解得,x1=2,x2=1.5,
当x=2时,3.5﹣x=1.5,此时长大于宽,符合实际;
当x=1.5时,3.5﹣x=2,此时长小于宽,不符合实际;
由上可得,矩形B的长为2,
故答案为:2.
17.解:(1)设月平均增长率为x,
依题意,得:1440(1+x)2=2250,
解得:x1=0.25=25%,x2=﹣2.25(不合题意,舍去).
答:月平均增长率是25%.
(2)设售价应降低y元,则每天可售出200+=(200+50y)千克,
依题意,得:(20﹣12﹣y)(200+50y)=1750,
整理,得:y2﹣4y+3=0,
解得:y1=1,y2=3.
∵要尽量减少库存,
∴y=3.
答:售价应降低3元.
18.解:(1)设该商品平均每月的价格增长率为m,
依题意,得:50(1+m)2=72,
解得:m1=0.2=20%,m2=﹣2.2(不合题意,舍去).
答:该商品平均每月的价格增长率为20%.
(2)依题意,得:(x﹣40)[188+(72﹣x)]=4000,
整理,得:x2﹣300x+14400=0,
解得:x1=60,x2=240.
∵商家需尽快将这批商品售出,
∴x=60.
答:x为60元时商品每天的利润可达到4000元.
19.解:(1)设经过x秒后,△PBQ的面积等于8cm2,则BP=(6﹣x)cm,BQ=2xcm,
依题意,得:(6﹣x)×2x=8,
化简,得:x2﹣6x+8=0,
解得:x1=2,x2=4.
答:经过2秒或4秒后,△PBQ的面积等于8cm2.
(2)设经过y秒后,P,Q两点间距离是cm,则BP=(6﹣y)cm,BQ=2ycm,
依题意,得:(6﹣y)2+(2y)2=()2,
化简,得:5y2﹣12y﹣17=0,
解得:y1=,y2=﹣1(不合题意,舍去).
答:经过秒后,P,Q两点间距离是cm.
20.解:(1)设AD=x米,则BC=AD=x米,
∴CD=34+2﹣2AD=34+2﹣2x=(36﹣2x)米.
故答案为:(36﹣2x).
(2)依题意得:x(36﹣2x)=160,
化简得:x2﹣18x+80=0,
解得:x1=8,x2=10.
当x=8时,36﹣2x=36﹣2×8=20>18,不合题意,舍去;
当x=10时,36﹣2x=36﹣2×10=16<18,符合题意.
答:AD的长为10米.
同步优生辅导训练(附答案)
1.“古越龙山”酿酒公司由于注重对市场调研和新产品的研发,新研制的某款瓶装酒获得市场的认可,今年四月份销售了50万瓶,按市场供需趋势预计今年二季度可销售182万瓶.设该款酒的销售量今年五、六月份平均每月的增长率为x,那么x满足的方程是( )
A.50(1+x)2=182
B.50+50(1+x)+50(1+x)2=182
C.50(1+2x)=182
D.50+50(1+x)+50(1+2x)2=182
2.某校初一年级开展了一班一特色活动,2001班以“地”为特色在学校的试验园地进行种植蔬菜活动.试验园的形状是长15米、宽8米的矩形,为便于管理,要在中间开辟一横两纵共三条等宽的小道,使种植面积为110平方米,则小道的宽为多少米?若设小道的宽为x米,则根据题意,列方程为( )
A.(15+2x)(8+x)=110
B.(15﹣2x)(8﹣x)=110
C.(15+x)(8+2x)=110
D.(15﹣x)(8﹣2x)=110
3.已知有1人患了某新型肺炎,经过两轮传染后共有256人患病,设每轮传染中平均一人传染x人,则可以列方程( )
A.1+2x=256
B.1+x2=256
C.(1+x)2=256
D.1+x=256
4.《九章算术》是我国古代数学的经典著作,它的出现标志着中国古代数学形成了完整的体系,其“勾股”章中记载了一个数学问题:“今有户高多于广六尺,两隅相去适一丈,问户高、广各几何?”译文为:“已知有一扇矩形门的高比宽多6尺,门的对角线长为1丈(1丈=10尺),那么门的高和宽各是多少?”如果设门的宽为x尺,则可列方程为( )
A.x2+(x+6)2=102
B.x2+(x+6)2=12
C.x2+(x﹣6)2=102
D.x2+(x﹣6)2=12
5.某小区花园有一块长方形花圃,它的宽为5m,若长边不变,将短边扩大,使得扩大后的花圃形状为正方形,且面积比原来增加15m2,设原来花圃长边为xm,可列方程( )
A.x?+5x=15
B.x2﹣5x=15
C.(x﹣5)2=15
D.x﹣25=15
6.元旦来临前,某商场将一件原价为a元的衬衫以一个给定的百分比提升价格,元旦那天商场又按照新的价格以相同的百分比降低了这件衬衫的价格,最终,衬衫的价格比原价降低了0.16a元,则这个给定的百分比为( )
A.16%
B.36%
C.40%
D.50%
7.某工厂2021年数字化改造总投入100万元,2023年总投入预计达到180万元,设年平均增长率为x,则可列方程为( )
A.100(1+x)=180
B.100(1+2x)=180
C.100(1+x+x2)=180
D.100(1+x)2=180
8.欧几里得在《几何原本》中,记载了用图解法解方程x2+ax=b2的方法,类似地我们可以用折纸的方法求方程x2+x﹣1=0的一个正根.如图,一张边长为1的正方形的纸片ABCD,先折出AD、BC的中点G、H,再折出线段AN,然后通过沿线段AN折叠使AD落在线段AH上,得到点D的新位置P,并连接NP、NH,此时,在下列四个选项中,有一条线段的长度恰好是方程x2+x﹣1=0的一个正根,则这条线段是( )
A.线段BH
B.线段DN
C.线段CN
D.线段NH
9.某校八年级组织篮球赛,若每两班之间赛一场,共进行了28场,则该校八年级有
个班级.
10.两个相邻偶数的积是168,则这两个相邻偶数中较大的数是
.
11.哈尔滨市某楼盘以每平方米10000元的均价对外销售,经过连续两次降价后,均价为每平方米8100元,则平均每次降价的百分率为
.
12.如图是一块矩形铁皮,将四个角各剪去一个边长为2米的正方形后剩下的部分做成一个容积为96立方米的无盖长方体箱子,已知长方体箱子底面的长比宽多2米,则矩形铁皮的面积为
平方米.
13.商场某种商品进价为120元/件,售价130元/件时,每天可销售70件;售价单价高于130元时,每涨价1元,日销售量就减少1件.据此,若销售单价为
元时,商场每天盈利达1500元.
14.中国古代数学家杨辉的《田亩比类乘除捷法》中记载:“直田积八百六十四步,只云阔不及长一十二步,问阔及长各几步?翻译成数学问题是:一块矩形田地的面积为864平方步,它的宽比长少12步,问它的长与宽各多少步?利用方程思想,设宽为x步,则依题意列方程为
.
15.已知3个连续整数的和为m,它们的平方和是n,且n=11(m﹣8),则m=
.
16.在研究:“任意给定一个矩形A,是否存在另一个矩形B,它的周长和面积分别是已知矩形周长和面积的一半”时,小明发现:当已知矩形A的长和宽分别为6和1时,存在一个矩形B的周长和面积分别是矩形A周长和面积的一半,那么矩形B的长为
.
17.2020年突如其来的新型冠状病毒疫情,给生鲜电商带来了意想不到的流量和机遇,据统计某生鲜电商平台1月份的销售额是1440万元,3月份的销售额是2250万元.
(1)若该平台1月份到3月份的月平均增长率都相同,求月平均增长率是多少?
(2)市场调查发现,某水果在“盒马鲜生”平台上的售价为20元/千克时,每天能销售200千克,售价每降价2元,每天可多售出100千克,为了推广宣传,商家决定降价促销,同时尽量减少库存,已知该水果的成本价为12元/千克,若使销售该水果每天获利1750元,则售价应降低多少元?
18.某商店以每件40元的价格进了一批热销商品,出售价格经过两个月的调整,从每件50元上涨到每件72元,此时每月可售出188件商品.
(1)求该商品平均每月的价格增长率;
(2)因某些原因,商家需尽快将这批商品售出,决定降价出售.经过市场调查发现:售价每下降一元,每个月多卖出一件,设实际售价为x元,则x为多少元时商品每月的利润可达到4000元.
19.如图所示,在Rt△ABC中,∠B=90°,AB=6cm,BC=8cm,点P由点A出发,沿AB边以1cm/s的速度向点B移动;点Q由点B出发,沿BC边以2cm/s的速度向点C移动.如果点P,Q分别从点A,B同时出发,问:
(1)经过几秒后,△PBQ的面积等于8cm2?
(2)经过几秒后,P,Q两点间距离是cm?
20.如图,依靠一面长18米的墙,用34米长的篱笆围成一个矩形场地花圃ABCD,AB边上留有2米宽的小门EF(用其他材料做,不用篱笆围).
(1)设花圃的一边AD长为x米,请你用含x的代数式表示另一边CD的长为
米;
(2)当矩形场地面积为160平方米时,求AD的长.
参考答案
1.解:依题意得五、六月份的销量产量为50(1+x)、50(1+x)2,
∴50+50(1+x)+50(1+x)2=182.
故选:B.
2.解:设小道的宽为x米,则6个小矩形可合成长为(15﹣2x)米、宽为(8﹣x)米的大矩形,
依题意得:(15﹣2x)(8﹣x)=110.
故选:B.
3.解:设每轮传染中平均一个人传染了x个人,
第一轮传染后患流感的人数是:1+x,
第二轮传染后患流感的人数是:1+x+x(1+x),
而已知经过两轮传染后共有256人患了流感,则可得方程,
1+x+x(1+x)=256,即(1+x)2=256.
故选:C.
4.解:设门的宽为x尺,那么这个门的高为(x+6)尺,根据题意得方程:
x2+(x+6)2=102,
故选:A.
5.解:设原来绿地的长边为x(m),根据题意得
x2﹣5x=15,
故选:B.
6.解:设这个给定的百分比为x,根据题意得,
a(1+x)(1﹣x)=a﹣0.16a,
解得x1=0.4,x2=﹣0.4(舍去),
即这个给定的百分比为40%.
故选:C.
7.解:设年平均增长率为x,则2022的数字化改造总投入为:100(1+x)万元,2023的数字化改造总投入为:100(1+x)2万元,那么可得方程:100(1+x)2=180.
故选:D.
8.解:设DN=m,则NC=1﹣m.
由题意可知:△ADN≌△APN,H是BC的中点,
∴DN=NP=m,CH=0.5.
∵S正方形=S△ABH+S△ADN+S△CHN+SANH,
∴1×1=×1×+×1×m+××(1﹣m)+××m,
∴m=.
∵x2+x﹣1=0的解为:x=﹣±,
∴取正值为x=.
∴这条线段是线段DN.
故选:B.
9.解:设八年级有x个班,
依题意得:x(x﹣1)=28,
整理得:x2﹣x﹣56=0,
解得:x1=8,x2=﹣7(不合题意,舍去).
则该校八年级有8个班级.
故答案为:8.
10.解:设这两个相邻偶数中较大的数是x,则另外一个偶数为(x﹣2),
依题意得:x(x﹣2)=168,
整理得:x?﹣2x﹣168=0,
解得:x1=14,x2=﹣12.
故答案为:14或﹣12.
11.解:设平均每次降价的百分率为x,
依题意得:10000(1﹣x)2=8100,
解得:x1=0.1=10%,x2=1.9(不合题意,舍去).
故答案为:10%.
12.解:设矩形铁皮的宽为x米,则长为(x+2)米,
依题意得:(x+2﹣2×2)(x﹣2×2)×2=96,
整理得:x2﹣6x﹣40=0,
解得:x1=﹣4(不合题意,舍去),x2=10,
∴(x+2)x=(10+2)×10=120(平方米).
故答案为:120.
13.解:设销售单价为x元,则每天可销售70﹣(x﹣130)=(200﹣x)件,
依题意得:(x﹣120)(200﹣x)=1500,
整理得:x2﹣320x+25500=0,
解得:x1=150,x2=170.
故答案为:150或170.
14.解:∵矩形的宽为x(步),且宽比长少12(步),
∴矩形的长为(x+12)(步).
依题意,得:x(x+12)=864.
故答案为:x(x+12)=864.
15.解:设三个整数分别为a,a+1,a+2,
所以
m=3a+3,n=a2+(a+1)2+(a+2)2=3a2+6a+5,
由n=11(m﹣8),
所以
3a2+6a+5=11(3a﹣5),
解得a=4或5,
则m=15或18.
16.解:由已知可得,
矩形A的周长是(6+1)×2=14,面积是6×1=6,
则矩形B的周长是7,面积是3,
设矩形B的长为x,则宽为3.5﹣x,
则x(3.5﹣x)=3,
解得,x1=2,x2=1.5,
当x=2时,3.5﹣x=1.5,此时长大于宽,符合实际;
当x=1.5时,3.5﹣x=2,此时长小于宽,不符合实际;
由上可得,矩形B的长为2,
故答案为:2.
17.解:(1)设月平均增长率为x,
依题意,得:1440(1+x)2=2250,
解得:x1=0.25=25%,x2=﹣2.25(不合题意,舍去).
答:月平均增长率是25%.
(2)设售价应降低y元,则每天可售出200+=(200+50y)千克,
依题意,得:(20﹣12﹣y)(200+50y)=1750,
整理,得:y2﹣4y+3=0,
解得:y1=1,y2=3.
∵要尽量减少库存,
∴y=3.
答:售价应降低3元.
18.解:(1)设该商品平均每月的价格增长率为m,
依题意,得:50(1+m)2=72,
解得:m1=0.2=20%,m2=﹣2.2(不合题意,舍去).
答:该商品平均每月的价格增长率为20%.
(2)依题意,得:(x﹣40)[188+(72﹣x)]=4000,
整理,得:x2﹣300x+14400=0,
解得:x1=60,x2=240.
∵商家需尽快将这批商品售出,
∴x=60.
答:x为60元时商品每天的利润可达到4000元.
19.解:(1)设经过x秒后,△PBQ的面积等于8cm2,则BP=(6﹣x)cm,BQ=2xcm,
依题意,得:(6﹣x)×2x=8,
化简,得:x2﹣6x+8=0,
解得:x1=2,x2=4.
答:经过2秒或4秒后,△PBQ的面积等于8cm2.
(2)设经过y秒后,P,Q两点间距离是cm,则BP=(6﹣y)cm,BQ=2ycm,
依题意,得:(6﹣y)2+(2y)2=()2,
化简,得:5y2﹣12y﹣17=0,
解得:y1=,y2=﹣1(不合题意,舍去).
答:经过秒后,P,Q两点间距离是cm.
20.解:(1)设AD=x米,则BC=AD=x米,
∴CD=34+2﹣2AD=34+2﹣2x=(36﹣2x)米.
故答案为:(36﹣2x).
(2)依题意得:x(36﹣2x)=160,
化简得:x2﹣18x+80=0,
解得:x1=8,x2=10.
当x=8时,36﹣2x=36﹣2×8=20>18,不合题意,舍去;
当x=10时,36﹣2x=36﹣2×10=16<18,符合题意.
答:AD的长为10米.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
