2021-2022学年北师大版八年级数学上册4.4.1借助一次函数解决简单实际问题同步练习题(word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版八年级数学上册4.4.1借助一次函数解决简单实际问题同步练习题(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 170.9KB | ||
| 资源类型 | 教案 | ||
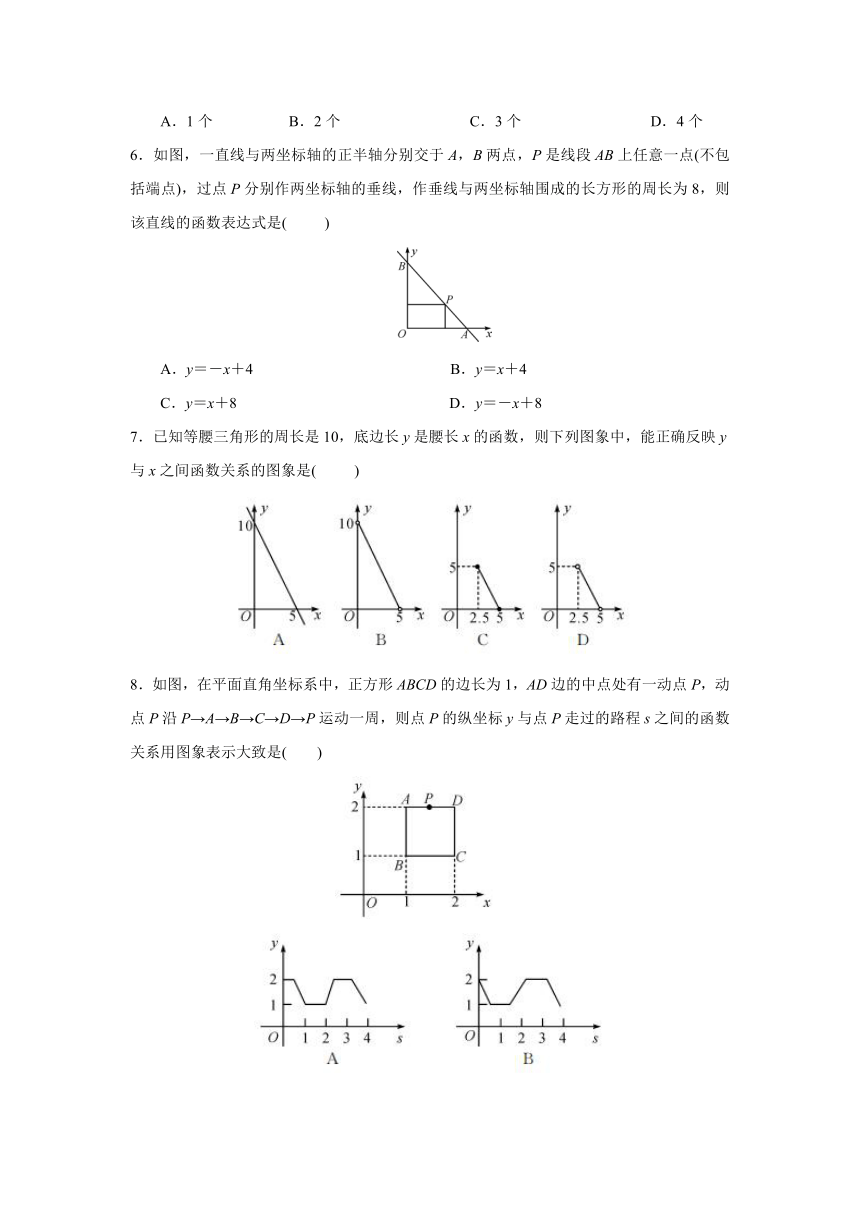
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-20 07:43:54 | ||
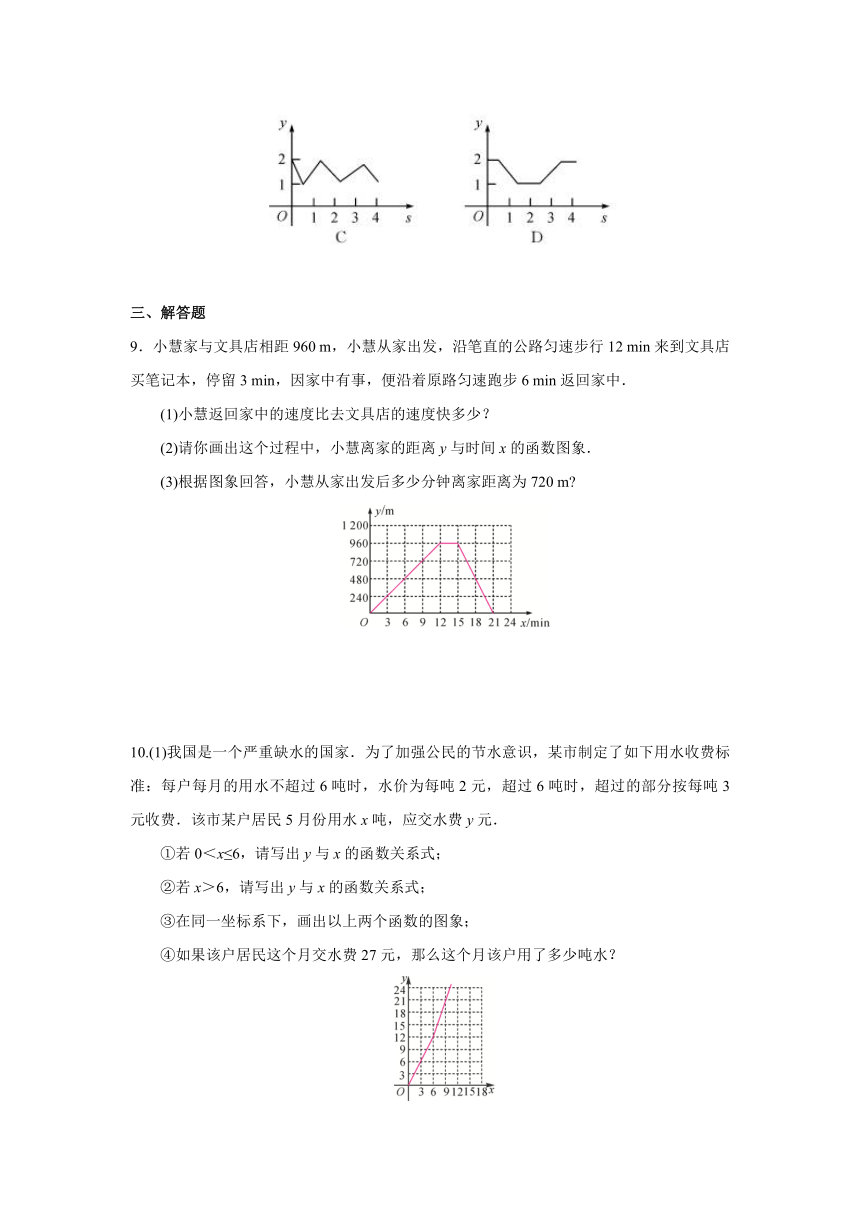
图片预览

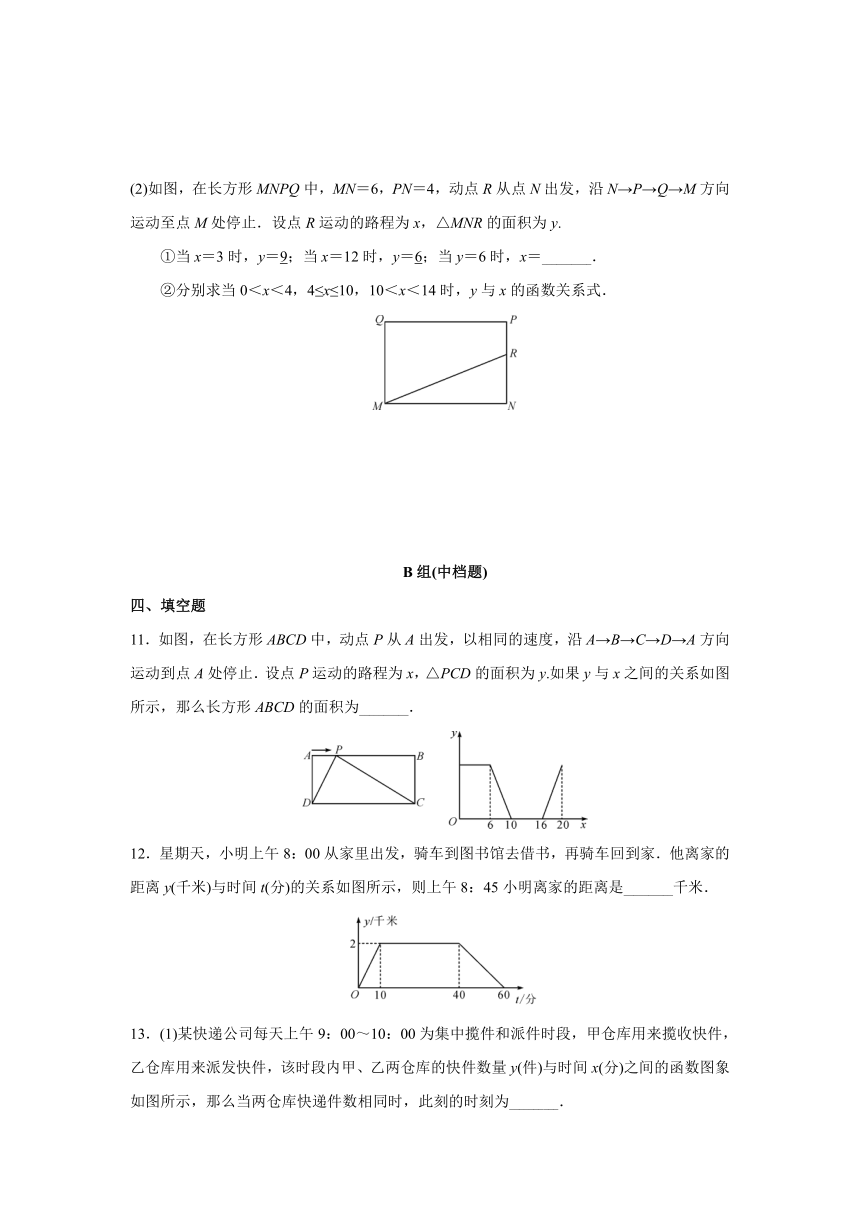

文档简介
4.4.1借助一次函数解决简单实际问题
同步练习题
2021-2022学年北师大版八年级数学上册
A组(基础题)
一、填空题
1.(1)已知一次函数y=2x-1的图象经过A(x1,1),B(x2,3)两点,则x1_____x2(填“>”“<”或“=”).
(2)已知点P(-m-1,m+1)关于x轴对称的点在第一象限,则一次函数y=(m+1)x+m2+1的图象不经过第_____象限.
2.(1)两名老师带领x名学生到动物园参观.已知成人票每张50元,学生票每张20元,设门票的总费用为y元,则y与x的函数关系式为__________.
(2)某市出租车白天的收费起步价为14元,即路程不超过3千米时收费14元,超过部分每千米收费2.4元.如果乘客白天乘坐出租车的路程为x(x>3)千米,乘车费为y元,那么y与x之间的关系式为__________.
3.(1)如图,在△ABC中,边BC的长为12,BC边上的高AD′为5,点D在BC上运动.设BD的长为x(0<x<12),则△ACD的面积y与x之间的关系式为__________.
(2)某产品每件的成本为30元,试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如下表:
x/元
40
50
60
…
y/件
80
70
60
…
若日销售量y是销售价x的一次函数,则日销售量y(件)与销售价x(元)的函数关系式为__________.
4.汽车开始行驶前,油箱内有油40升,汽车开始行驶后,每小时耗油5升.
(1)油箱内剩余油量Q(升)与行驶时间t(时)之间的函数关系式为__________;
(2)油箱内的油最多可供汽车行驶__________小时.
二、选择题
5.有下列函数表达式:①y=-2x+1;②y=6-x;③y=-;④y=(1-)x.其中y随x的增大而减小的有(
)
A.1个
B.2个
C.3个
D.4个
6.如图,一直线与两坐标轴的正半轴分别交于A,B两点,P是线段AB上任意一点(不包括端点),过点P分别作两坐标轴的垂线,作垂线与两坐标轴围成的长方形的周长为8,则该直线的函数表达式是(
)
A.y=-x+4
B.y=x+4
C.y=x+8
D.y=-x+8
7.已知等腰三角形的周长是10,底边长y是腰长x的函数,则下列图象中,能正确反映y与x之间函数关系的图象是(
)
8.如图,在平面直角坐标系中,正方形ABCD的边长为1,AD边的中点处有一动点P,动点P沿P→A→B→C→D→P运动一周,则点P的纵坐标y与点P走过的路程s之间的函数关系用图象表示大致是(
)
三、解答题
9.小慧家与文具店相距960
m,小慧从家出发,沿笔直的公路匀速步行12
min来到文具店买笔记本,停留3
min,因家中有事,便沿着原路匀速跑步6
min返回家中.
(1)小慧返回家中的速度比去文具店的速度快多少?
(2)请你画出这个过程中,小慧离家的距离y与时间x的函数图象.
(3)根据图象回答,小慧从家出发后多少分钟离家距离为720
m?
10.(1)我国是一个严重缺水的国家.为了加强公民的节水意识,某市制定了如下用水收费标准:每户每月的用水不超过6吨时,水价为每吨2元,超过6吨时,超过的部分按每吨3元收费.该市某户居民5月份用水x吨,应交水费y元.
①若0<x≤6,请写出y与x的函数关系式;
②若x>6,请写出y与x的函数关系式;
③在同一坐标系下,画出以上两个函数的图象;
④如果该户居民这个月交水费27元,那么这个月该户用了多少吨水?
(2)如图,在长方形MNPQ中,MN=6,PN=4,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.设点R运动的路程为x,△MNR的面积为y.
①当x=3时,y=9;当x=12时,y=6;当y=6时,x=__________.
②分别求当0<x<4,4≤x≤10,10<x<14时,y与x的函数关系式.
B组(中档题)
四、填空题
11.如图,在长方形ABCD中,动点P从A出发,以相同的速度,沿A→B→C→D→A方向运动到点A处停止.设点P运动的路程为x,△PCD的面积为y.如果y与x之间的关系如图所示,那么长方形ABCD的面积为__________.
12.星期天,小明上午8:00从家里出发,骑车到图书馆去借书,再骑车回到家.他离家的距离y(千米)与时间t(分)的关系如图所示,则上午8:45小明离家的距离是__________千米.
13.(1)某快递公司每天上午9:00~10:00为集中揽件和派件时段,甲仓库用来揽收快件,乙仓库用来派发快件,该时段内甲、乙两仓库的快件数量y(件)与时间x(分)之间的函数图象如图所示,那么当两仓库快递件数相同时,此刻的时刻为__________.
(2)图1是甲、乙两个圆柱形水槽的轴截面示意图,乙槽中有一圆柱体铁块立放其中(圆柱形铁块的下底面完全落在乙槽底面上).现将甲槽中的水匀速注入乙槽,甲、乙两个水槽中水的深度y(厘米)与注水时间x(分)之间的关系如图2所示.①图2中折线ABC表示乙槽中水的深度与注水时间之间的关系(选填“甲”或“乙”);②点B的纵坐标表示的实际意义是__________.
五、解答题
14.如图,正方形ABCD的边长为4,点E是AB的中点,点P从点E出发,沿E→A→D→C移动至终点C.设P点经过的路径长为x,△CPE的面积为y,求y与x之间的函数关系式.
C组(综合题)
15.甲、乙两个批发店销售同一种苹果,在甲批发店,不论一次购买数量是多少,价格均为6元/千克.在乙批发店,一次购买数量不超过50千克时,价格为7元/千克;一次购买数量超过50千克时,其中有50千克的价格仍为7元/千克,超过50千克部分的价格为5元/千克.设小王在同一个批发店一次购买苹果的数量为x千克(x>0).
(1)根据题意填表:
一次购买数量/千克
30
50
150
…
甲批发店花费/元
180
…
乙批发店花费/元
…
(2)设在甲批发店花费y1元,在乙批发店花费y2元,分别求y1,y2关于x的函数表达式.
(3)根据题意填空:
①若小王在甲批发店和在乙批发店一次购买苹果的数量相同,且花费相同,则他在同一个批发店一次购买苹果的数量为__________
千克;
②若小王在同一个批发店一次购买苹果的数量为120千克,则他在甲、乙两个批发店中的乙批发店购买花费少;
③若小王在同一个批发店一次购买苹果花费了360元,则他在甲、乙两个批发店中的甲批发店购买数量多.
参考答案
A组(基础题)
一、填空题
1.(1)(2020·宿迁)已知一次函数y=2x-1的图象经过A(x1,1),B(x2,3)两点,则x1<x2(填“>”“<”或“=”).
(2)已知点P(-m-1,m+1)关于x轴对称的点在第一象限,则一次函数y=(m+1)x+m2+1的图象不经过第三象限.
2.(1)两名老师带领x名学生到动物园参观.已知成人票每张50元,学生票每张20元,设门票的总费用为y元,则y与x的函数关系式为y=20x+100.
(2)某市出租车白天的收费起步价为14元,即路程不超过3千米时收费14元,超过部分每千米收费2.4元.如果乘客白天乘坐出租车的路程为x(x>3)千米,乘车费为y元,那么y与x之间的关系式为y=2.4x+6.8.
3.(1)如图,在△ABC中,边BC的长为12,BC边上的高AD′为5,点D在BC上运动.设BD的长为x(0<x<12),则△ACD的面积y与x之间的关系式为y=-x+30.
(2)某产品每件的成本为30元,试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如下表:
x/元
40
50
60
…
y/件
80
70
60
…
若日销售量y是销售价x的一次函数,则日销售量y(件)与销售价x(元)的函数关系式为y=-x+120.
4.汽车开始行驶前,油箱内有油40升,汽车开始行驶后,每小时耗油5升.
(1)油箱内剩余油量Q(升)与行驶时间t(时)之间的函数关系式为Q=40-5t(0≤t≤8);
(2)油箱内的油最多可供汽车行驶8小时.
二、选择题
5.有下列函数表达式:①y=-2x+1;②y=6-x;③y=-;④y=(1-)x.其中y随x的增大而减小的有(
D
)
A.1个
B.2个
C.3个
D.4个
6.如图,一直线与两坐标轴的正半轴分别交于A,B两点,P是线段AB上任意一点(不包括端点),过点P分别作两坐标轴的垂线,作垂线与两坐标轴围成的长方形的周长为8,则该直线的函数表达式是(
A
)
A.y=-x+4
B.y=x+4
C.y=x+8
D.y=-x+8
7.已知等腰三角形的周长是10,底边长y是腰长x的函数,则下列图象中,能正确反映y与x之间函数关系的图象是(
D
)
8.如图,在平面直角坐标系中,正方形ABCD的边长为1,AD边的中点处有一动点P,动点P沿P→A→B→C→D→P运动一周,则点P的纵坐标y与点P走过的路程s之间的函数关系用图象表示大致是(
D
)
三、解答题
9.小慧家与文具店相距960
m,小慧从家出发,沿笔直的公路匀速步行12
min来到文具店买笔记本,停留3
min,因家中有事,便沿着原路匀速跑步6
min返回家中.
(1)小慧返回家中的速度比去文具店的速度快多少?
(2)请你画出这个过程中,小慧离家的距离y与时间x的函数图象.
(3)根据图象回答,小慧从家出发后多少分钟离家距离为720
m?
解:(1)小慧返回家中的速度比去文具店的速度快-=80(m/min).
(2)如图所示.
(3)根据图象可得,小慧从家出发后9
min或16.5
min离家距离为720
m.
10.(1)我国是一个严重缺水的国家.为了加强公民的节水意识,某市制定了如下用水收费标准:每户每月的用水不超过6吨时,水价为每吨2元,超过6吨时,超过的部分按每吨3元收费.该市某户居民5月份用水x吨,应交水费y元.
①若0<x≤6,请写出y与x的函数关系式;
②若x>6,请写出y与x的函数关系式;
③在同一坐标系下,画出以上两个函数的图象;
④如果该户居民这个月交水费27元,那么这个月该户用了多少吨水?
解:①当0<x≤6,y=2x.
②当x>6,y=2×6+3(x-6)=3x-6,即y=3x-6.
③如图所示.
④∵27>12,
∴该户用水量超过6吨.
∴3x-6=27,解得x=11.
答:这个月该户用了11吨水.
(2)如图,在长方形MNPQ中,MN=6,PN=4,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.设点R运动的路程为x,△MNR的面积为y.
①当x=3时,y=9;当x=12时,y=6;当y=6时,x=2或12.
②分别求当0<x<4,4≤x≤10,10<x<14时,y与x的函数关系式.
解:当0≤x<4时,R在PN上运动,y=MN·RN=×6×x=3x;
当4≤x≤10时,R在QP上运动,y=MN·PN=×6×4=12;
当10<x≤14时,R在QM上运动,y=MN·RM=×6×[4-(x-10)]=42-3x.
B组(中档题)
四、填空题
11.如图,在长方形ABCD中,动点P从A出发,以相同的速度,沿A→B→C→D→A方向运动到点A处停止.设点P运动的路程为x,△PCD的面积为y.如果y与x之间的关系如图所示,那么长方形ABCD的面积为24.
12.星期天,小明上午8:00从家里出发,骑车到图书馆去借书,再骑车回到家.他离家的距离y(千米)与时间t(分)的关系如图所示,则上午8:45小明离家的距离是1.5千米.
13.(1)某快递公司每天上午9:00~10:00为集中揽件和派件时段,甲仓库用来揽收快件,乙仓库用来派发快件,该时段内甲、乙两仓库的快件数量y(件)与时间x(分)之间的函数图象如图所示,那么当两仓库快递件数相同时,此刻的时刻为9:20.
(2)图1是甲、乙两个圆柱形水槽的轴截面示意图,乙槽中有一圆柱体铁块立放其中(圆柱形铁块的下底面完全落在乙槽底面上).现将甲槽中的水匀速注入乙槽,甲、乙两个水槽中水的深度y(厘米)与注水时间x(分)之间的关系如图2所示.①图2中折线ABC表示乙槽中水的深度与注水时间之间的关系(选填“甲”或“乙”);②点B的纵坐标表示的实际意义是铁块的高度.
五、解答题
14.如图,正方形ABCD的边长为4,点E是AB的中点,点P从点E出发,沿E→A→D→C移动至终点C.设P点经过的路径长为x,△CPE的面积为y,求y与x之间的函数关系式.
解:∵正方形ABCD的边长为4,E为AB的中点,
∴AE=2.
①当点P在AE上时,0≤x≤2,
∵点P经过的路径长为x,∴PE=x.
∴y=S△CPE=PE·BC=×x×4=2x.
②当点P在AD上时,2<x≤6,
∵点P经过的路径长为x.
∴AP=x-2,DP=6-x.
∴y=S△CPE=S正方形ABCD-S△BEC-S△APE-S△PDC
=4×4-×2×4-×2×(x-2)
-×4×(6-x)=16-4-x+2-12+2x=x+2.
③当点P在DC上时,6<x≤10,
∵点P经过的路径长为x,
∴PD=x-6,PC=10-x.
∴y=S△OPE=PC·BC=×(10-x)×4=-2x+20.
综上所述,y与x之间的函数关系式为
y=
C组(综合题)
15.甲、乙两个批发店销售同一种苹果,在甲批发店,不论一次购买数量是多少,价格均为6元/千克.在乙批发店,一次购买数量不超过50千克时,价格为7元/千克;一次购买数量超过50千克时,其中有50千克的价格仍为7元/千克,超过50千克部分的价格为5元/千克.设小王在同一个批发店一次购买苹果的数量为x千克(x>0).
(1)根据题意填表:
一次购买数量/千克
30
50
150
…
甲批发店花费/元
180
300
900
…
乙批发店花费/元
210
350
850
…
(2)设在甲批发店花费y1元,在乙批发店花费y2元,分别求y1,y2关于x的函数表达式.
(3)根据题意填空:
①若小王在甲批发店和在乙批发店一次购买苹果的数量相同,且花费相同,则他在同一个批发店一次购买苹果的数量为100
千克;
②若小王在同一个批发店一次购买苹果的数量为120千克,则他在甲、乙两个批发店中的乙批发店购买花费少;
③若小王在同一个批发店一次购买苹果花费了360元,则他在甲、乙两个批发店中的甲批发店购买数量多.
解:y1=6x(x>0).
当0<x≤50时,y2=7x;
当x>50时,y2=7×50+5(x-50)=5x+100.
因此y1,y2与x的函数表达式为y1=6x(x>0),
y2=
同步练习题
2021-2022学年北师大版八年级数学上册
A组(基础题)
一、填空题
1.(1)已知一次函数y=2x-1的图象经过A(x1,1),B(x2,3)两点,则x1_____x2(填“>”“<”或“=”).
(2)已知点P(-m-1,m+1)关于x轴对称的点在第一象限,则一次函数y=(m+1)x+m2+1的图象不经过第_____象限.
2.(1)两名老师带领x名学生到动物园参观.已知成人票每张50元,学生票每张20元,设门票的总费用为y元,则y与x的函数关系式为__________.
(2)某市出租车白天的收费起步价为14元,即路程不超过3千米时收费14元,超过部分每千米收费2.4元.如果乘客白天乘坐出租车的路程为x(x>3)千米,乘车费为y元,那么y与x之间的关系式为__________.
3.(1)如图,在△ABC中,边BC的长为12,BC边上的高AD′为5,点D在BC上运动.设BD的长为x(0<x<12),则△ACD的面积y与x之间的关系式为__________.
(2)某产品每件的成本为30元,试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如下表:
x/元
40
50
60
…
y/件
80
70
60
…
若日销售量y是销售价x的一次函数,则日销售量y(件)与销售价x(元)的函数关系式为__________.
4.汽车开始行驶前,油箱内有油40升,汽车开始行驶后,每小时耗油5升.
(1)油箱内剩余油量Q(升)与行驶时间t(时)之间的函数关系式为__________;
(2)油箱内的油最多可供汽车行驶__________小时.
二、选择题
5.有下列函数表达式:①y=-2x+1;②y=6-x;③y=-;④y=(1-)x.其中y随x的增大而减小的有(
)
A.1个
B.2个
C.3个
D.4个
6.如图,一直线与两坐标轴的正半轴分别交于A,B两点,P是线段AB上任意一点(不包括端点),过点P分别作两坐标轴的垂线,作垂线与两坐标轴围成的长方形的周长为8,则该直线的函数表达式是(
)
A.y=-x+4
B.y=x+4
C.y=x+8
D.y=-x+8
7.已知等腰三角形的周长是10,底边长y是腰长x的函数,则下列图象中,能正确反映y与x之间函数关系的图象是(
)
8.如图,在平面直角坐标系中,正方形ABCD的边长为1,AD边的中点处有一动点P,动点P沿P→A→B→C→D→P运动一周,则点P的纵坐标y与点P走过的路程s之间的函数关系用图象表示大致是(
)
三、解答题
9.小慧家与文具店相距960
m,小慧从家出发,沿笔直的公路匀速步行12
min来到文具店买笔记本,停留3
min,因家中有事,便沿着原路匀速跑步6
min返回家中.
(1)小慧返回家中的速度比去文具店的速度快多少?
(2)请你画出这个过程中,小慧离家的距离y与时间x的函数图象.
(3)根据图象回答,小慧从家出发后多少分钟离家距离为720
m?
10.(1)我国是一个严重缺水的国家.为了加强公民的节水意识,某市制定了如下用水收费标准:每户每月的用水不超过6吨时,水价为每吨2元,超过6吨时,超过的部分按每吨3元收费.该市某户居民5月份用水x吨,应交水费y元.
①若0<x≤6,请写出y与x的函数关系式;
②若x>6,请写出y与x的函数关系式;
③在同一坐标系下,画出以上两个函数的图象;
④如果该户居民这个月交水费27元,那么这个月该户用了多少吨水?
(2)如图,在长方形MNPQ中,MN=6,PN=4,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.设点R运动的路程为x,△MNR的面积为y.
①当x=3时,y=9;当x=12时,y=6;当y=6时,x=__________.
②分别求当0<x<4,4≤x≤10,10<x<14时,y与x的函数关系式.
B组(中档题)
四、填空题
11.如图,在长方形ABCD中,动点P从A出发,以相同的速度,沿A→B→C→D→A方向运动到点A处停止.设点P运动的路程为x,△PCD的面积为y.如果y与x之间的关系如图所示,那么长方形ABCD的面积为__________.
12.星期天,小明上午8:00从家里出发,骑车到图书馆去借书,再骑车回到家.他离家的距离y(千米)与时间t(分)的关系如图所示,则上午8:45小明离家的距离是__________千米.
13.(1)某快递公司每天上午9:00~10:00为集中揽件和派件时段,甲仓库用来揽收快件,乙仓库用来派发快件,该时段内甲、乙两仓库的快件数量y(件)与时间x(分)之间的函数图象如图所示,那么当两仓库快递件数相同时,此刻的时刻为__________.
(2)图1是甲、乙两个圆柱形水槽的轴截面示意图,乙槽中有一圆柱体铁块立放其中(圆柱形铁块的下底面完全落在乙槽底面上).现将甲槽中的水匀速注入乙槽,甲、乙两个水槽中水的深度y(厘米)与注水时间x(分)之间的关系如图2所示.①图2中折线ABC表示乙槽中水的深度与注水时间之间的关系(选填“甲”或“乙”);②点B的纵坐标表示的实际意义是__________.
五、解答题
14.如图,正方形ABCD的边长为4,点E是AB的中点,点P从点E出发,沿E→A→D→C移动至终点C.设P点经过的路径长为x,△CPE的面积为y,求y与x之间的函数关系式.
C组(综合题)
15.甲、乙两个批发店销售同一种苹果,在甲批发店,不论一次购买数量是多少,价格均为6元/千克.在乙批发店,一次购买数量不超过50千克时,价格为7元/千克;一次购买数量超过50千克时,其中有50千克的价格仍为7元/千克,超过50千克部分的价格为5元/千克.设小王在同一个批发店一次购买苹果的数量为x千克(x>0).
(1)根据题意填表:
一次购买数量/千克
30
50
150
…
甲批发店花费/元
180
…
乙批发店花费/元
…
(2)设在甲批发店花费y1元,在乙批发店花费y2元,分别求y1,y2关于x的函数表达式.
(3)根据题意填空:
①若小王在甲批发店和在乙批发店一次购买苹果的数量相同,且花费相同,则他在同一个批发店一次购买苹果的数量为__________
千克;
②若小王在同一个批发店一次购买苹果的数量为120千克,则他在甲、乙两个批发店中的乙批发店购买花费少;
③若小王在同一个批发店一次购买苹果花费了360元,则他在甲、乙两个批发店中的甲批发店购买数量多.
参考答案
A组(基础题)
一、填空题
1.(1)(2020·宿迁)已知一次函数y=2x-1的图象经过A(x1,1),B(x2,3)两点,则x1<x2(填“>”“<”或“=”).
(2)已知点P(-m-1,m+1)关于x轴对称的点在第一象限,则一次函数y=(m+1)x+m2+1的图象不经过第三象限.
2.(1)两名老师带领x名学生到动物园参观.已知成人票每张50元,学生票每张20元,设门票的总费用为y元,则y与x的函数关系式为y=20x+100.
(2)某市出租车白天的收费起步价为14元,即路程不超过3千米时收费14元,超过部分每千米收费2.4元.如果乘客白天乘坐出租车的路程为x(x>3)千米,乘车费为y元,那么y与x之间的关系式为y=2.4x+6.8.
3.(1)如图,在△ABC中,边BC的长为12,BC边上的高AD′为5,点D在BC上运动.设BD的长为x(0<x<12),则△ACD的面积y与x之间的关系式为y=-x+30.
(2)某产品每件的成本为30元,试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如下表:
x/元
40
50
60
…
y/件
80
70
60
…
若日销售量y是销售价x的一次函数,则日销售量y(件)与销售价x(元)的函数关系式为y=-x+120.
4.汽车开始行驶前,油箱内有油40升,汽车开始行驶后,每小时耗油5升.
(1)油箱内剩余油量Q(升)与行驶时间t(时)之间的函数关系式为Q=40-5t(0≤t≤8);
(2)油箱内的油最多可供汽车行驶8小时.
二、选择题
5.有下列函数表达式:①y=-2x+1;②y=6-x;③y=-;④y=(1-)x.其中y随x的增大而减小的有(
D
)
A.1个
B.2个
C.3个
D.4个
6.如图,一直线与两坐标轴的正半轴分别交于A,B两点,P是线段AB上任意一点(不包括端点),过点P分别作两坐标轴的垂线,作垂线与两坐标轴围成的长方形的周长为8,则该直线的函数表达式是(
A
)
A.y=-x+4
B.y=x+4
C.y=x+8
D.y=-x+8
7.已知等腰三角形的周长是10,底边长y是腰长x的函数,则下列图象中,能正确反映y与x之间函数关系的图象是(
D
)
8.如图,在平面直角坐标系中,正方形ABCD的边长为1,AD边的中点处有一动点P,动点P沿P→A→B→C→D→P运动一周,则点P的纵坐标y与点P走过的路程s之间的函数关系用图象表示大致是(
D
)
三、解答题
9.小慧家与文具店相距960
m,小慧从家出发,沿笔直的公路匀速步行12
min来到文具店买笔记本,停留3
min,因家中有事,便沿着原路匀速跑步6
min返回家中.
(1)小慧返回家中的速度比去文具店的速度快多少?
(2)请你画出这个过程中,小慧离家的距离y与时间x的函数图象.
(3)根据图象回答,小慧从家出发后多少分钟离家距离为720
m?
解:(1)小慧返回家中的速度比去文具店的速度快-=80(m/min).
(2)如图所示.
(3)根据图象可得,小慧从家出发后9
min或16.5
min离家距离为720
m.
10.(1)我国是一个严重缺水的国家.为了加强公民的节水意识,某市制定了如下用水收费标准:每户每月的用水不超过6吨时,水价为每吨2元,超过6吨时,超过的部分按每吨3元收费.该市某户居民5月份用水x吨,应交水费y元.
①若0<x≤6,请写出y与x的函数关系式;
②若x>6,请写出y与x的函数关系式;
③在同一坐标系下,画出以上两个函数的图象;
④如果该户居民这个月交水费27元,那么这个月该户用了多少吨水?
解:①当0<x≤6,y=2x.
②当x>6,y=2×6+3(x-6)=3x-6,即y=3x-6.
③如图所示.
④∵27>12,
∴该户用水量超过6吨.
∴3x-6=27,解得x=11.
答:这个月该户用了11吨水.
(2)如图,在长方形MNPQ中,MN=6,PN=4,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.设点R运动的路程为x,△MNR的面积为y.
①当x=3时,y=9;当x=12时,y=6;当y=6时,x=2或12.
②分别求当0<x<4,4≤x≤10,10<x<14时,y与x的函数关系式.
解:当0≤x<4时,R在PN上运动,y=MN·RN=×6×x=3x;
当4≤x≤10时,R在QP上运动,y=MN·PN=×6×4=12;
当10<x≤14时,R在QM上运动,y=MN·RM=×6×[4-(x-10)]=42-3x.
B组(中档题)
四、填空题
11.如图,在长方形ABCD中,动点P从A出发,以相同的速度,沿A→B→C→D→A方向运动到点A处停止.设点P运动的路程为x,△PCD的面积为y.如果y与x之间的关系如图所示,那么长方形ABCD的面积为24.
12.星期天,小明上午8:00从家里出发,骑车到图书馆去借书,再骑车回到家.他离家的距离y(千米)与时间t(分)的关系如图所示,则上午8:45小明离家的距离是1.5千米.
13.(1)某快递公司每天上午9:00~10:00为集中揽件和派件时段,甲仓库用来揽收快件,乙仓库用来派发快件,该时段内甲、乙两仓库的快件数量y(件)与时间x(分)之间的函数图象如图所示,那么当两仓库快递件数相同时,此刻的时刻为9:20.
(2)图1是甲、乙两个圆柱形水槽的轴截面示意图,乙槽中有一圆柱体铁块立放其中(圆柱形铁块的下底面完全落在乙槽底面上).现将甲槽中的水匀速注入乙槽,甲、乙两个水槽中水的深度y(厘米)与注水时间x(分)之间的关系如图2所示.①图2中折线ABC表示乙槽中水的深度与注水时间之间的关系(选填“甲”或“乙”);②点B的纵坐标表示的实际意义是铁块的高度.
五、解答题
14.如图,正方形ABCD的边长为4,点E是AB的中点,点P从点E出发,沿E→A→D→C移动至终点C.设P点经过的路径长为x,△CPE的面积为y,求y与x之间的函数关系式.
解:∵正方形ABCD的边长为4,E为AB的中点,
∴AE=2.
①当点P在AE上时,0≤x≤2,
∵点P经过的路径长为x,∴PE=x.
∴y=S△CPE=PE·BC=×x×4=2x.
②当点P在AD上时,2<x≤6,
∵点P经过的路径长为x.
∴AP=x-2,DP=6-x.
∴y=S△CPE=S正方形ABCD-S△BEC-S△APE-S△PDC
=4×4-×2×4-×2×(x-2)
-×4×(6-x)=16-4-x+2-12+2x=x+2.
③当点P在DC上时,6<x≤10,
∵点P经过的路径长为x,
∴PD=x-6,PC=10-x.
∴y=S△OPE=PC·BC=×(10-x)×4=-2x+20.
综上所述,y与x之间的函数关系式为
y=
C组(综合题)
15.甲、乙两个批发店销售同一种苹果,在甲批发店,不论一次购买数量是多少,价格均为6元/千克.在乙批发店,一次购买数量不超过50千克时,价格为7元/千克;一次购买数量超过50千克时,其中有50千克的价格仍为7元/千克,超过50千克部分的价格为5元/千克.设小王在同一个批发店一次购买苹果的数量为x千克(x>0).
(1)根据题意填表:
一次购买数量/千克
30
50
150
…
甲批发店花费/元
180
300
900
…
乙批发店花费/元
210
350
850
…
(2)设在甲批发店花费y1元,在乙批发店花费y2元,分别求y1,y2关于x的函数表达式.
(3)根据题意填空:
①若小王在甲批发店和在乙批发店一次购买苹果的数量相同,且花费相同,则他在同一个批发店一次购买苹果的数量为100
千克;
②若小王在同一个批发店一次购买苹果的数量为120千克,则他在甲、乙两个批发店中的乙批发店购买花费少;
③若小王在同一个批发店一次购买苹果花费了360元,则他在甲、乙两个批发店中的甲批发店购买数量多.
解:y1=6x(x>0).
当0<x≤50时,y2=7x;
当x>50时,y2=7×50+5(x-50)=5x+100.
因此y1,y2与x的函数表达式为y1=6x(x>0),
y2=
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
