2021-2022学年北师大版八年级数学上册 5.3应用二元一次方程组——鸡兔同笼 同步练习题(word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版八年级数学上册 5.3应用二元一次方程组——鸡兔同笼 同步练习题(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 223.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-20 08:07:16 | ||
图片预览




文档简介
5.3应用二元一次方程组——鸡兔同笼同步练习题
2021-2022学年北师大版八年级数学上册
A组(基础题)
一、填空题
1.《算法统宗》是中国古代数学名著,作者是明代著名数学家程大位.其中有这样的记载了这样一道数学题:“一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚各几丁?”译文:有100名和尚分100个馒头,正好分完.如果大和尚一人分3个,小和尚3人分一个,试问大、小和尚各有几人?设有大和尚x人,小和尚y人,可列方程组为______.
2.某学校有两种类型的学生宿舍30间,大宿舍每间可以住8人,小宿舍每间可以住5人,该学校共有198个住宿生,恰好可以住满这30间宿舍.若设有大宿舍x间,有小宿舍y间,则可以列出的方程组为______.
3.现有古代数学问题:“今有牛五羊二值金八两,牛二羊五值金六两,则牛一羊一值金______两.”
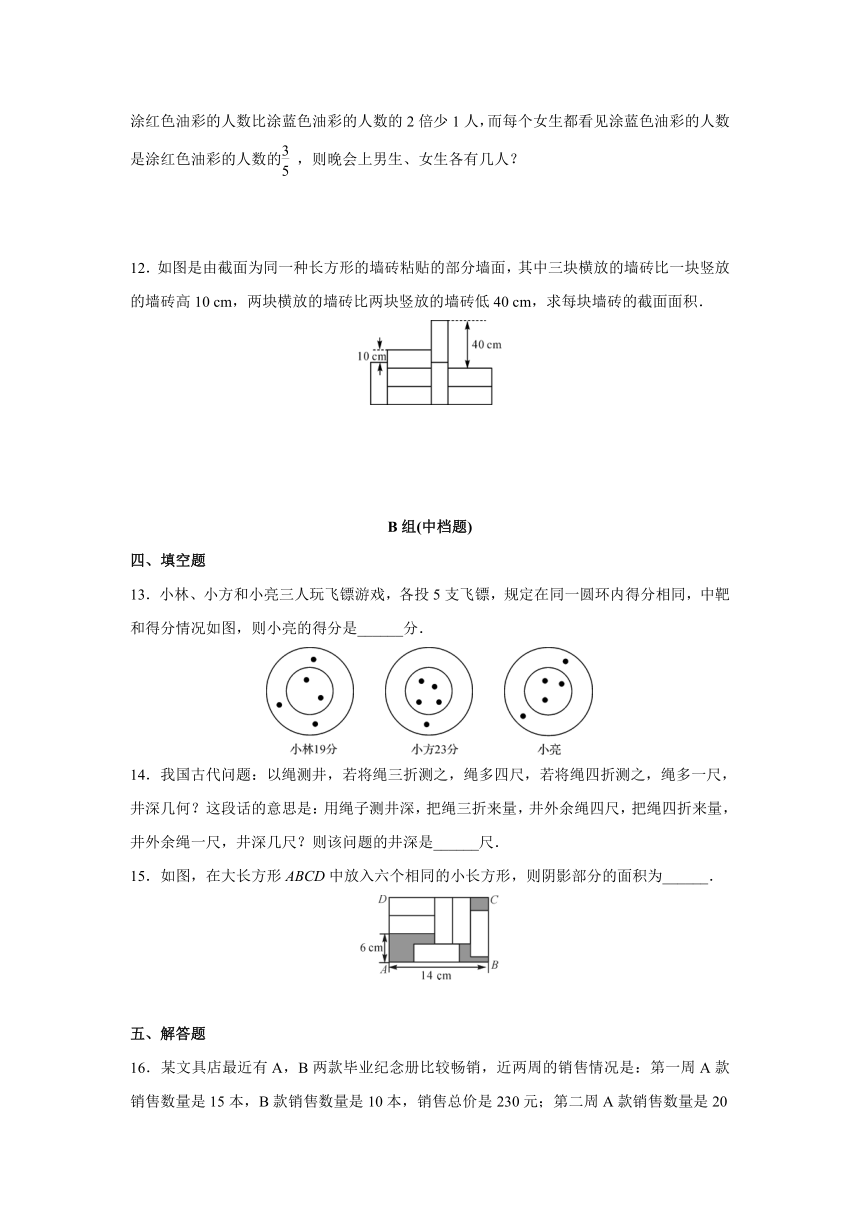
4.如图,商店里把塑料凳整齐地叠放在一起,据图中信息,当有10张塑料凳整齐地叠放在一起时的高度是______cm.
二、选择题
5.学校的篮球数比排球数的2倍少3个,篮球数与排球数的比是3∶2,求两种球各有多少个.若设篮球有x个,排球有y个,根据题意列方程组为(
)
A.
B.
C.
D.
6.“十一”国庆期间,学校组织466名八年级学生参加社会实践活动,现已准备了49座和37座两种客车共10辆,刚好坐满,设49座客车x辆,37座客车y辆.根据题意,得(
)
A.
B.
C.
D.
7.如图,将正方形ABCD的一角折叠,折痕为AE,∠BAD比∠BAE大48°.设∠BAE和∠BAD的度数分别为x°,y°,那么x,y所适合的一个方程组是(
)
A.
B.
C.
D.
8.我国古代数学著作《增删算法统宗》记载了一个“绳索量竿”问题:“一条竿子一条索,索比竿子长一托.折回索子却量竿,却比竿子短一托.”其大意为:现有一根竿和一条绳索,用绳索去量竿,绳索比竿长5尺;如果将绳索对半折后再去量竿,就比竿短5尺.设绳索长x尺,竿长y尺,则符合题意的方程组是(
)
A.
B.
C.
D.
三、解答题
9.疫情无情人有情,八方相助暖人心.一爱心人士向某社区捐赠了A品牌一次性医用口罩5
000个和B品牌免洗消毒液100瓶,总价值18
000元.已知10个A品牌一次性医用口罩与1瓶B品牌免洗消毒液共需84元.求A品牌一次性医用口罩和B品牌免洗消毒液的单价分别是多少?
10.“两果问价”问题出自我国古代算书《四元玉鉴》,原题如下:九百九十九文钱,甜果苦果买一千,甜果九个十一文,苦果七个四文钱,试问甜苦果几个?又问各该几个钱?将题目译成白话文,内容如下:九百九十九文钱买了甜果和苦果共一千个,已知十一文钱可买九个甜果,四文钱可买七个苦果,那么甜果、苦果各买了多少个?买甜果和苦果各需要多少文钱?
11.某化装晚会上,男生脸上涂蓝色油彩,女生脸上涂红色油彩,游戏时,每个男生都看见涂红色油彩的人数比涂蓝色油彩的人数的2倍少1人,而每个女生都看见涂蓝色油彩的人数是涂红色油彩的人数的,则晚会上男生、女生各有几人?
12.如图是由截面为同一种长方形的墙砖粘贴的部分墙面,其中三块横放的墙砖比一块竖放的墙砖高10
cm,两块横放的墙砖比两块竖放的墙砖低40
cm,求每块墙砖的截面面积.
B组(中档题)
四、填空题
13.小林、小方和小亮三人玩飞镖游戏,各投5支飞镖,规定在同一圆环内得分相同,中靶和得分情况如图,则小亮的得分是______分.
14.我国古代问题:以绳测井,若将绳三折测之,绳多四尺,若将绳四折测之,绳多一尺,井深几何?这段话的意思是:用绳子测井深,把绳三折来量,井外余绳四尺,把绳四折来量,井外余绳一尺,井深几尺?则该问题的井深是______尺.
15.如图,在大长方形ABCD中放入六个相同的小长方形,则阴影部分的面积为______.
五、解答题
16.某文具店最近有A,B两款毕业纪念册比较畅销,近两周的销售情况是:第一周A款销售数量是15本,B款销售数量是10本,销售总价是230元;第二周A款销售数量是20本,B款销售数量是10本,销售总价是280元.
(1)求A,B两款毕业纪念册的销售单价.
(2)若某班准备用不超过529元购买这两种款式的毕业纪念册共60本,求最多能够买多少本A款毕业纪念册.
C组(综合题)
17.阅读理解
(Ⅰ)我国古代很早就开始对一次方程组进行研究,其中不少成果被收录在中国古代数学著作《九章算术》中,它的方程章中就有许多关于一次方程组的内容.
下面的两幅算筹图就表示了两个二元一次方程组:
把它们写成我们现在的方程组是与
(Ⅱ)对于二元一次方程组我们可以将x,y的系数和相应的常数项排成一个数表,通过运算使数表变为,即可求得的方程组的解为用数表简化解二元一次方程组的过程如下:
∴方程组的解为
解答下列问题:
(1)直接写出下面算筹图表示的关于x,y的二元一次方程组.
(2)依照阅读材料(Ⅱ)中数表的解法格式解(Ⅰ)中你写出的二元一次方程组.
参考答案
5.3应用二元一次方程组——鸡兔同笼同步练习题
2021-2022学年北师大版八年级数学上册
A组(基础题)
一、填空题
1.《算法统宗》是中国古代数学名著,作者是明代著名数学家程大位.其中有这样的记载了这样一道数学题:“一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚各几丁?”译文:有100名和尚分100个馒头,正好分完.如果大和尚一人分3个,小和尚3人分一个,试问大、小和尚各有几人?设有大和尚x人,小和尚y人,可列方程组为.
2.某学校有两种类型的学生宿舍30间,大宿舍每间可以住8人,小宿舍每间可以住5人,该学校共有198个住宿生,恰好可以住满这30间宿舍.若设有大宿舍x间,有小宿舍y间,则可以列出的方程组为.
3.现有古代数学问题:“今有牛五羊二值金八两,牛二羊五值金六两,则牛一羊一值金二两.”
4.如图,商店里把塑料凳整齐地叠放在一起,据图中信息,当有10张塑料凳整齐地叠放在一起时的高度是50cm.
二、选择题
5.学校的篮球数比排球数的2倍少3个,篮球数与排球数的比是3∶2,求两种球各有多少个.若设篮球有x个,排球有y个,根据题意列方程组为(
D
)
A.
B.
C.
D.
6.“十一”国庆期间,学校组织466名八年级学生参加社会实践活动,现已准备了49座和37座两种客车共10辆,刚好坐满,设49座客车x辆,37座客车y辆.根据题意,得(
A
)
A.
B.
C.
D.
7.如图,将正方形ABCD的一角折叠,折痕为AE,∠BAD比∠BAE大48°.设∠BAE和∠BAD的度数分别为x°,y°,那么x,y所适合的一个方程组是(
A
)
A.
B.
C.
D.
8.我国古代数学著作《增删算法统宗》记载了一个“绳索量竿”问题:“一条竿子一条索,索比竿子长一托.折回索子却量竿,却比竿子短一托.”其大意为:现有一根竿和一条绳索,用绳索去量竿,绳索比竿长5尺;如果将绳索对半折后再去量竿,就比竿短5尺.设绳索长x尺,竿长y尺,则符合题意的方程组是(
A
)
A.
B.
C.
D.
三、解答题
9.疫情无情人有情,八方相助暖人心.一爱心人士向某社区捐赠了A品牌一次性医用口罩5
000个和B品牌免洗消毒液100瓶,总价值18
000元.已知10个A品牌一次性医用口罩与1瓶B品牌免洗消毒液共需84元.求A品牌一次性医用口罩和B品牌免洗消毒液的单价分别是多少?
解:设A品牌一次性医用口罩单价是x元/个,B品牌免洗消毒液的单价是y元,根据题意,得
解得
答:A品牌一次性医用口罩单价是2.4元,B品牌免洗消毒液的单价是60元.
10.“两果问价”问题出自我国古代算书《四元玉鉴》,原题如下:九百九十九文钱,甜果苦果买一千,甜果九个十一文,苦果七个四文钱,试问甜苦果几个?又问各该几个钱?将题目译成白话文,内容如下:九百九十九文钱买了甜果和苦果共一千个,已知十一文钱可买九个甜果,四文钱可买七个苦果,那么甜果、苦果各买了多少个?买甜果和苦果各需要多少文钱?
解:设甜果买了x个,苦果买了y个,依题意,得
解得
∴x=803,y=196.
答:甜果买了657个,需要803文钱;苦果买了343个,需要196文钱.
11.某化装晚会上,男生脸上涂蓝色油彩,女生脸上涂红色油彩,游戏时,每个男生都看见涂红色油彩的人数比涂蓝色油彩的人数的2倍少1人,而每个女生都看见涂蓝色油彩的人数是涂红色油彩的人数的,则晚会上男生、女生各有几人?
解:设晚会上男生有x人,女生有y人,由题意,得
解得
答:晚会上男生有12人,女生有21人.
12.如图是由截面为同一种长方形的墙砖粘贴的部分墙面,其中三块横放的墙砖比一块竖放的墙砖高10
cm,两块横放的墙砖比两块竖放的墙砖低40
cm,求每块墙砖的截面面积.
解:设每块墙砖截面的长为x
cm,宽为y
cm.根据题意,得
解得
∴每块墙砖的截面面积是35×15=525(cm2).
答:每块墙砖的截面积是525
cm2.
B组(中档题)
四、填空题
13.小林、小方和小亮三人玩飞镖游戏,各投5支飞镖,规定在同一圆环内得分相同,中靶和得分情况如图,则小亮的得分是21分.
14.我国古代问题:以绳测井,若将绳三折测之,绳多四尺,若将绳四折测之,绳多一尺,井深几何?这段话的意思是:用绳子测井深,把绳三折来量,井外余绳四尺,把绳四折来量,井外余绳一尺,井深几尺?则该问题的井深是8尺.
15.如图,在大长方形ABCD中放入六个相同的小长方形,则阴影部分的面积为44____cm2.
五、解答题
16.某文具店最近有A,B两款毕业纪念册比较畅销,近两周的销售情况是:第一周A款销售数量是15本,B款销售数量是10本,销售总价是230元;第二周A款销售数量是20本,B款销售数量是10本,销售总价是280元.
(1)求A,B两款毕业纪念册的销售单价.
(2)若某班准备用不超过529元购买这两种款式的毕业纪念册共60本,求最多能够买多少本A款毕业纪念册.
解:(1)设A款毕业纪念册的销售单价为x元,B款毕业纪念册的销售单价为y元.根据题意,得
解得
答:A款毕业纪念册的销售单价为10元,B款毕业纪念册的销售单价为8元.
(2)设购买a本A款毕业纪念册,则购买(60-a)本B款毕业纪念册.根据题意,得
10a+8(60-a)≤529,解得a≤24.5.
∴最多能够买24本A款毕业纪念册.
C组(综合题)
17.阅读理解
(Ⅰ)我国古代很早就开始对一次方程组进行研究,其中不少成果被收录在中国古代数学著作《九章算术》中,它的方程章中就有许多关于一次方程组的内容.
下面的两幅算筹图就表示了两个二元一次方程组:
把它们写成我们现在的方程组是与
(Ⅱ)对于二元一次方程组我们可以将x,y的系数和相应的常数项排成一个数表,通过运算使数表变为,即可求得的方程组的解为用数表简化解二元一次方程组的过程如下:
∴方程组的解为
解答下列问题:
(1)直接写出下面算筹图表示的关于x,y的二元一次方程组.
(2)依照阅读材料(Ⅱ)中数表的解法格式解(Ⅰ)中你写出的二元一次方程组.
解:(1)
(2)
∴方程组的解为
2021-2022学年北师大版八年级数学上册
A组(基础题)
一、填空题
1.《算法统宗》是中国古代数学名著,作者是明代著名数学家程大位.其中有这样的记载了这样一道数学题:“一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚各几丁?”译文:有100名和尚分100个馒头,正好分完.如果大和尚一人分3个,小和尚3人分一个,试问大、小和尚各有几人?设有大和尚x人,小和尚y人,可列方程组为______.
2.某学校有两种类型的学生宿舍30间,大宿舍每间可以住8人,小宿舍每间可以住5人,该学校共有198个住宿生,恰好可以住满这30间宿舍.若设有大宿舍x间,有小宿舍y间,则可以列出的方程组为______.
3.现有古代数学问题:“今有牛五羊二值金八两,牛二羊五值金六两,则牛一羊一值金______两.”
4.如图,商店里把塑料凳整齐地叠放在一起,据图中信息,当有10张塑料凳整齐地叠放在一起时的高度是______cm.
二、选择题
5.学校的篮球数比排球数的2倍少3个,篮球数与排球数的比是3∶2,求两种球各有多少个.若设篮球有x个,排球有y个,根据题意列方程组为(
)
A.
B.
C.
D.
6.“十一”国庆期间,学校组织466名八年级学生参加社会实践活动,现已准备了49座和37座两种客车共10辆,刚好坐满,设49座客车x辆,37座客车y辆.根据题意,得(
)
A.
B.
C.
D.
7.如图,将正方形ABCD的一角折叠,折痕为AE,∠BAD比∠BAE大48°.设∠BAE和∠BAD的度数分别为x°,y°,那么x,y所适合的一个方程组是(
)
A.
B.
C.
D.
8.我国古代数学著作《增删算法统宗》记载了一个“绳索量竿”问题:“一条竿子一条索,索比竿子长一托.折回索子却量竿,却比竿子短一托.”其大意为:现有一根竿和一条绳索,用绳索去量竿,绳索比竿长5尺;如果将绳索对半折后再去量竿,就比竿短5尺.设绳索长x尺,竿长y尺,则符合题意的方程组是(
)
A.
B.
C.
D.
三、解答题
9.疫情无情人有情,八方相助暖人心.一爱心人士向某社区捐赠了A品牌一次性医用口罩5
000个和B品牌免洗消毒液100瓶,总价值18
000元.已知10个A品牌一次性医用口罩与1瓶B品牌免洗消毒液共需84元.求A品牌一次性医用口罩和B品牌免洗消毒液的单价分别是多少?
10.“两果问价”问题出自我国古代算书《四元玉鉴》,原题如下:九百九十九文钱,甜果苦果买一千,甜果九个十一文,苦果七个四文钱,试问甜苦果几个?又问各该几个钱?将题目译成白话文,内容如下:九百九十九文钱买了甜果和苦果共一千个,已知十一文钱可买九个甜果,四文钱可买七个苦果,那么甜果、苦果各买了多少个?买甜果和苦果各需要多少文钱?
11.某化装晚会上,男生脸上涂蓝色油彩,女生脸上涂红色油彩,游戏时,每个男生都看见涂红色油彩的人数比涂蓝色油彩的人数的2倍少1人,而每个女生都看见涂蓝色油彩的人数是涂红色油彩的人数的,则晚会上男生、女生各有几人?
12.如图是由截面为同一种长方形的墙砖粘贴的部分墙面,其中三块横放的墙砖比一块竖放的墙砖高10
cm,两块横放的墙砖比两块竖放的墙砖低40
cm,求每块墙砖的截面面积.
B组(中档题)
四、填空题
13.小林、小方和小亮三人玩飞镖游戏,各投5支飞镖,规定在同一圆环内得分相同,中靶和得分情况如图,则小亮的得分是______分.
14.我国古代问题:以绳测井,若将绳三折测之,绳多四尺,若将绳四折测之,绳多一尺,井深几何?这段话的意思是:用绳子测井深,把绳三折来量,井外余绳四尺,把绳四折来量,井外余绳一尺,井深几尺?则该问题的井深是______尺.
15.如图,在大长方形ABCD中放入六个相同的小长方形,则阴影部分的面积为______.
五、解答题
16.某文具店最近有A,B两款毕业纪念册比较畅销,近两周的销售情况是:第一周A款销售数量是15本,B款销售数量是10本,销售总价是230元;第二周A款销售数量是20本,B款销售数量是10本,销售总价是280元.
(1)求A,B两款毕业纪念册的销售单价.
(2)若某班准备用不超过529元购买这两种款式的毕业纪念册共60本,求最多能够买多少本A款毕业纪念册.
C组(综合题)
17.阅读理解
(Ⅰ)我国古代很早就开始对一次方程组进行研究,其中不少成果被收录在中国古代数学著作《九章算术》中,它的方程章中就有许多关于一次方程组的内容.
下面的两幅算筹图就表示了两个二元一次方程组:
把它们写成我们现在的方程组是与
(Ⅱ)对于二元一次方程组我们可以将x,y的系数和相应的常数项排成一个数表,通过运算使数表变为,即可求得的方程组的解为用数表简化解二元一次方程组的过程如下:
∴方程组的解为
解答下列问题:
(1)直接写出下面算筹图表示的关于x,y的二元一次方程组.
(2)依照阅读材料(Ⅱ)中数表的解法格式解(Ⅰ)中你写出的二元一次方程组.
参考答案
5.3应用二元一次方程组——鸡兔同笼同步练习题
2021-2022学年北师大版八年级数学上册
A组(基础题)
一、填空题
1.《算法统宗》是中国古代数学名著,作者是明代著名数学家程大位.其中有这样的记载了这样一道数学题:“一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚各几丁?”译文:有100名和尚分100个馒头,正好分完.如果大和尚一人分3个,小和尚3人分一个,试问大、小和尚各有几人?设有大和尚x人,小和尚y人,可列方程组为.
2.某学校有两种类型的学生宿舍30间,大宿舍每间可以住8人,小宿舍每间可以住5人,该学校共有198个住宿生,恰好可以住满这30间宿舍.若设有大宿舍x间,有小宿舍y间,则可以列出的方程组为.
3.现有古代数学问题:“今有牛五羊二值金八两,牛二羊五值金六两,则牛一羊一值金二两.”
4.如图,商店里把塑料凳整齐地叠放在一起,据图中信息,当有10张塑料凳整齐地叠放在一起时的高度是50cm.
二、选择题
5.学校的篮球数比排球数的2倍少3个,篮球数与排球数的比是3∶2,求两种球各有多少个.若设篮球有x个,排球有y个,根据题意列方程组为(
D
)
A.
B.
C.
D.
6.“十一”国庆期间,学校组织466名八年级学生参加社会实践活动,现已准备了49座和37座两种客车共10辆,刚好坐满,设49座客车x辆,37座客车y辆.根据题意,得(
A
)
A.
B.
C.
D.
7.如图,将正方形ABCD的一角折叠,折痕为AE,∠BAD比∠BAE大48°.设∠BAE和∠BAD的度数分别为x°,y°,那么x,y所适合的一个方程组是(
A
)
A.
B.
C.
D.
8.我国古代数学著作《增删算法统宗》记载了一个“绳索量竿”问题:“一条竿子一条索,索比竿子长一托.折回索子却量竿,却比竿子短一托.”其大意为:现有一根竿和一条绳索,用绳索去量竿,绳索比竿长5尺;如果将绳索对半折后再去量竿,就比竿短5尺.设绳索长x尺,竿长y尺,则符合题意的方程组是(
A
)
A.
B.
C.
D.
三、解答题
9.疫情无情人有情,八方相助暖人心.一爱心人士向某社区捐赠了A品牌一次性医用口罩5
000个和B品牌免洗消毒液100瓶,总价值18
000元.已知10个A品牌一次性医用口罩与1瓶B品牌免洗消毒液共需84元.求A品牌一次性医用口罩和B品牌免洗消毒液的单价分别是多少?
解:设A品牌一次性医用口罩单价是x元/个,B品牌免洗消毒液的单价是y元,根据题意,得
解得
答:A品牌一次性医用口罩单价是2.4元,B品牌免洗消毒液的单价是60元.
10.“两果问价”问题出自我国古代算书《四元玉鉴》,原题如下:九百九十九文钱,甜果苦果买一千,甜果九个十一文,苦果七个四文钱,试问甜苦果几个?又问各该几个钱?将题目译成白话文,内容如下:九百九十九文钱买了甜果和苦果共一千个,已知十一文钱可买九个甜果,四文钱可买七个苦果,那么甜果、苦果各买了多少个?买甜果和苦果各需要多少文钱?
解:设甜果买了x个,苦果买了y个,依题意,得
解得
∴x=803,y=196.
答:甜果买了657个,需要803文钱;苦果买了343个,需要196文钱.
11.某化装晚会上,男生脸上涂蓝色油彩,女生脸上涂红色油彩,游戏时,每个男生都看见涂红色油彩的人数比涂蓝色油彩的人数的2倍少1人,而每个女生都看见涂蓝色油彩的人数是涂红色油彩的人数的,则晚会上男生、女生各有几人?
解:设晚会上男生有x人,女生有y人,由题意,得
解得
答:晚会上男生有12人,女生有21人.
12.如图是由截面为同一种长方形的墙砖粘贴的部分墙面,其中三块横放的墙砖比一块竖放的墙砖高10
cm,两块横放的墙砖比两块竖放的墙砖低40
cm,求每块墙砖的截面面积.
解:设每块墙砖截面的长为x
cm,宽为y
cm.根据题意,得
解得
∴每块墙砖的截面面积是35×15=525(cm2).
答:每块墙砖的截面积是525
cm2.
B组(中档题)
四、填空题
13.小林、小方和小亮三人玩飞镖游戏,各投5支飞镖,规定在同一圆环内得分相同,中靶和得分情况如图,则小亮的得分是21分.
14.我国古代问题:以绳测井,若将绳三折测之,绳多四尺,若将绳四折测之,绳多一尺,井深几何?这段话的意思是:用绳子测井深,把绳三折来量,井外余绳四尺,把绳四折来量,井外余绳一尺,井深几尺?则该问题的井深是8尺.
15.如图,在大长方形ABCD中放入六个相同的小长方形,则阴影部分的面积为44____cm2.
五、解答题
16.某文具店最近有A,B两款毕业纪念册比较畅销,近两周的销售情况是:第一周A款销售数量是15本,B款销售数量是10本,销售总价是230元;第二周A款销售数量是20本,B款销售数量是10本,销售总价是280元.
(1)求A,B两款毕业纪念册的销售单价.
(2)若某班准备用不超过529元购买这两种款式的毕业纪念册共60本,求最多能够买多少本A款毕业纪念册.
解:(1)设A款毕业纪念册的销售单价为x元,B款毕业纪念册的销售单价为y元.根据题意,得
解得
答:A款毕业纪念册的销售单价为10元,B款毕业纪念册的销售单价为8元.
(2)设购买a本A款毕业纪念册,则购买(60-a)本B款毕业纪念册.根据题意,得
10a+8(60-a)≤529,解得a≤24.5.
∴最多能够买24本A款毕业纪念册.
C组(综合题)
17.阅读理解
(Ⅰ)我国古代很早就开始对一次方程组进行研究,其中不少成果被收录在中国古代数学著作《九章算术》中,它的方程章中就有许多关于一次方程组的内容.
下面的两幅算筹图就表示了两个二元一次方程组:
把它们写成我们现在的方程组是与
(Ⅱ)对于二元一次方程组我们可以将x,y的系数和相应的常数项排成一个数表,通过运算使数表变为,即可求得的方程组的解为用数表简化解二元一次方程组的过程如下:
∴方程组的解为
解答下列问题:
(1)直接写出下面算筹图表示的关于x,y的二元一次方程组.
(2)依照阅读材料(Ⅱ)中数表的解法格式解(Ⅰ)中你写出的二元一次方程组.
解:(1)
(2)
∴方程组的解为
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
