用列举法求概率

(共26张PPT)
求概率的方法
复习：下列事件中哪些事件是随机事件？哪些事件是必然事件？哪些是不可能事件？
⑴抛出的铅球会下落
（２）某运动员百米赛跑的成绩为２秒
（３）买到的电影票，座位号为单号
（４）ｘ２＋１是正数
（５）投掷硬币时，国徽朝上
必然事件
不可能事件
随机事件
必然事件
随机事件
概率
事件发生的可能性可以用数值来表示
P（必然事件）
P（不可能事件）
P（随机事件）
=1
=0
=x(0复习回顾：
一般地，如果在一次试验中，
有n种可能的结果，并且它们发生的可能性都相等，
事件A包含在其中的m种结果，
那么事件A发生的概率为：
求概率的步骤：
(1)列举出一次试验中的所有结果(n个)；
(2)找出其中事件A发生的结果(m个)；
(3)运用公式求事件A的概率：
解：
在甲袋中，P（取出黑球）＝
＝
在乙袋中，P（取出黑球）＝
＝
＞
所以，选乙袋成功的机会大。
20红，8黑
甲袋
20红,15黑,10白
乙袋
球除了颜色以外没有任何区别。两袋中的球都搅匀。蒙上眼睛从口袋中取一只球，如果你想取出1只黑球，你选哪个口袋成功的机会大呢？
小佳在游戏开始时，踩中后出现如图所示的情况。
我们把与标号3的方格相临的方格记为A区域(画线部分)，
A区域外的部分记为B区域。
数字3表示A区域有3颗地雷，
那么第二步应踩在A区域还是B区域？
3
A区域
如图是“扫雷”游戏。
在 9×9 个正方形雷区中，
随机埋藏着10颗地雷，
每个方格最多只能藏一颗地雷。
B区域
引例：掷两枚硬币，求下列事件的概率：
(1)两枚硬币全部正面朝上；
(2)两枚硬币全部反面朝上；
(3)一枚硬币正面朝上，一枚硬币反面朝上；
“掷两枚硬币”共有几种结果？
正正
正反
反正
反反
为了不重不漏地列出所有这些结果,
你有什么好办法么？
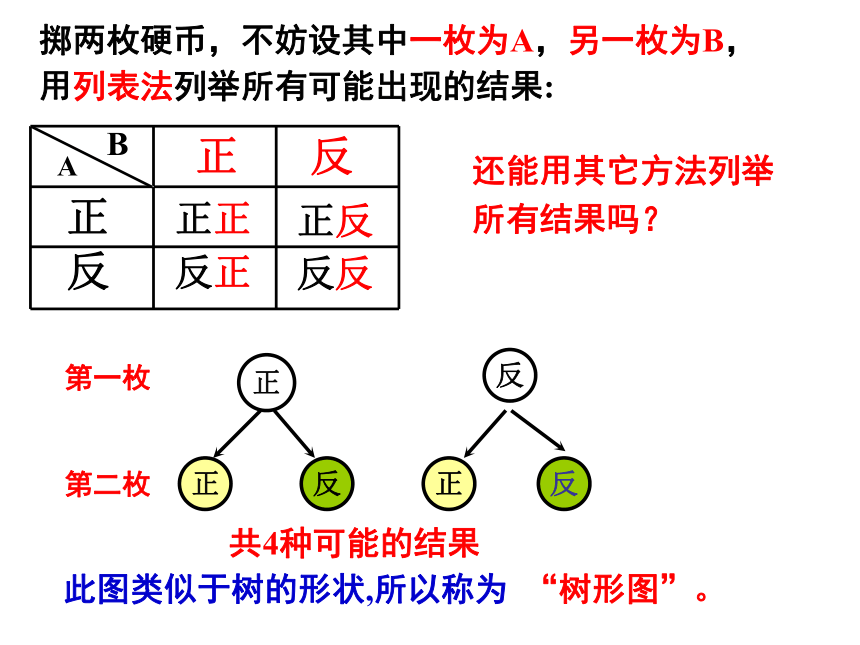
掷两枚硬币，不妨设其中一枚为A，另一枚为B，
用列表法列举所有可能出现的结果:
B
A
还能用其它方法列举
所有结果吗？
正
反
正
反
正正
正反
反正
反反
反
正
第一枚
第二枚
反
正
反
正
共4种可能的结果
此图类似于树的形状,所以称为 “树形图”。
甲
乙
1
2
3
4
5
6
7
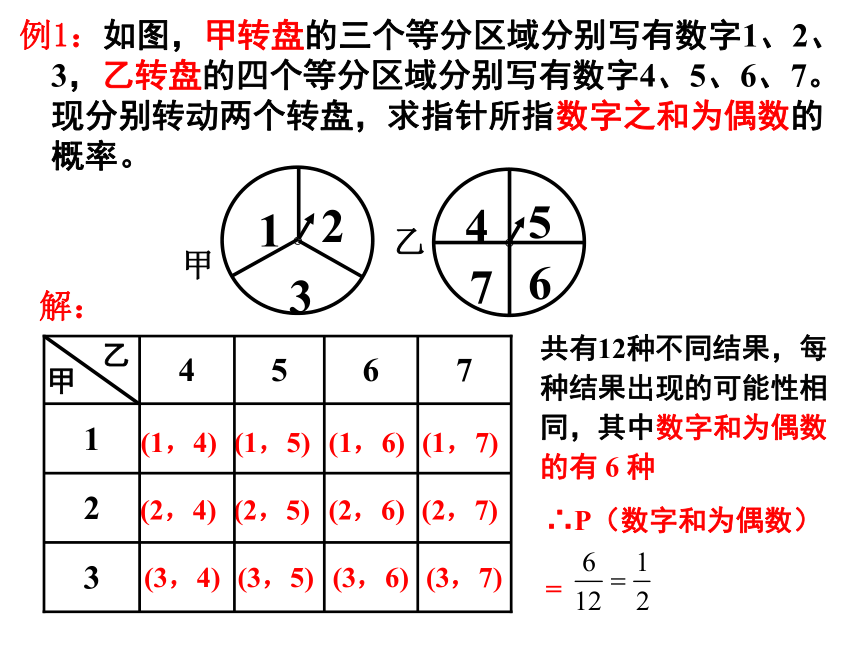
例1：如图，甲转盘的三个等分区域分别写有数字1、2、3，乙转盘的四个等分区域分别写有数字4、5、6、7。现分别转动两个转盘，求指针所指数字之和为偶数的概率。
解：
(1，4)
(1，5)
(1，6)
(1，7)
(2，4)
(2，5)
(2，6)
(2，7)
(3，4)
(3，5)
(3，6)
(3，7)
共有12种不同结果，每种结果出现的可能性相同，其中数字和为偶数的有 6 种
∴P（数字和为偶数）
=
3
2
1
7
6
5
4
甲
乙
归纳
“列表法”的意义：
当试验涉及两个因素(例如两个转盘)
并且可能出现的结果数目较多时，
为不重不漏地列出所有的结果，
通常采用“列表法”。
上题可以用画“树形图”的方法
列举所有可能的结果么？
探究
3
1
甲转盘
乙转盘
4
共 12 种可能的结果
与“列表”法对比，结果怎么样？
甲转盘指针所指的数字可能是 1、2、3，
乙转盘指针所指的数字可能是 4、5、6、7。
甲
1
2
3
乙
4
5
6
7
2
5
6
7
4
5
6
7
4
5
6
7
求指针所指数字之和为偶数的概率。
√
√
√
√
√
√
例2、同时掷两个质地相同的骰子，计算下列事件的概率：
(1)两个骰子的点数相同；(2)两个骰子的点数和是9；
(3)至少有个骰子的点数是2。
解：
1 2 3 4 5 6
1 (1,1) (2,1) (3,1) (4,1) (5,1) (6,1)
2 (1,2) (2,2) (3,2) (4,2) (5,2) (6,2)
3 (1,3) (2,3) (3,3) (4,3) (5,3) (6,3)
4 (1,4) (2,4) (3,4) (4,4) (5,4) (6,4)
5 (1,5) (2,5) (3,5) (4,5) (5,5) (6,5)
6 (1,6) (2,6) (3,6) (4,6) (5,5) (6,6)
二
一
此题用列树图的方法好吗？
P(点数相同）=
P(点数和是9）=
P(至少有个骰子的点数是2 ）=
思考
“同时掷两个质地相同的骰子”与
“把一个骰子掷两次”，所得到的结果有变化吗？
“同时掷两个质地相同的骰子”
两个骰子各出现的点数为1～6点
“把一个骰子掷两次”
两次骰子各出现的点数仍为1～6点
归纳
“两个相同的随机事件同时发生”与
“一个随机事件先后两次发生”的结果是一样的。
随机事件“同时”与“先后”的关系：
1、一只蚂蚁在如图所示的树枝上寻觅食物，假定蚂蚁在每个岔口都会随机地选择一条路径，它获得食物的概率是多少？
蚂蚁
食物
练习
2、用如图所示的两个转盘进行“配紫色”(红与蓝)游戏。请你采用“树形图”法计算配得紫色的概率。
甲
乙
白
红
蓝
蓝
黄
绿
红
3、每个转盘分成相等的两个扇形。甲、乙两人利用它们做游戏：同时转动两个转盘，
如果两个指针所停区域的颜色相同则甲获胜；
如果两个指针所停区域的颜色不同则乙获胜。
你认为这个游戏公平吗？
黄
蓝
黄
蓝
绿
蓝
5、一个袋子中装有2个红球和2个绿球，任意摸出一个球，记录颜色后放回，再任意摸出一个球，请你计算两次都摸到红球的概率。
若第一次摸出一球后，不放回，结果又会怎样？
“放回”与“不放回”的区别：
(1)“放回”可以看作两次相同的试验；
(2)“不放回”则看作两次不同的试验。
4.一个口袋内装有大小相等的1个白球和已编有不同号码的3个黑球，从中摸出2个球.摸出两个黑球的概率是多少？
黑2
黑1
白
黑3
黑1
黑3
黑2
黑3
白
黑1
黑2
白
黑1
黑3
白
黑2
解：设三个黑球分别为：黑1、黑2、黑3，则：
第一个球：
第二个球：
P（摸出两个黑球）=
4、在盒子中有三张卡片，随机抽取两张，可能拼出菱形(两张三角形)也可能拼出房子(一张三角形和一张正方形)。游戏规则是：
若拼成菱形，甲胜；若拼成房子，乙胜。
你认为这个游戏公平吗？
7、甲、乙两人各掷一枚质量分布均匀的正方体骰子，如果点数
之积为奇数，那么甲得1分；如果点数之积为偶数，那么乙得1分。
连续投10次，谁得分高，谁就获胜。
(1)请你想一想，谁获胜的机会大？并说明理由；
(2)你认为游戏公平吗？如果不公平，请你设计一个公平的游戏。
1 2 3 4 5 6
1 1×1=1 2×1=2 3×1=3 4×1=4 5×1=5 6×1=6
2 1×2=2 2×2=4 3×2=6 4×2=8 5×2=10 6×2=12
3 1×3=3 2×3=6 3×3=9 4×3=12 5×3=15 6×3=18
4 1×4=4 2×4=8 3×4=12 4×4=16 5×4=20 6×4=24
5 1×5=5 2×5=10 3×5=15 4×5=20 5×5=25 6×5=30
6 1×6=6 2×6=12 3×6=18 4×6=24 5×6=30 6×6=36
列出所有可能的结果：
小结
1.“列表法”的意义
3.随机事件“同时”与“先后”的关系;
“放回”与“不放回”的关系.
2. 利用树图列举所有结果的方法.
1、在6张卡片上分别写有1～6的整数，随机地抽取一张后放回，再随机地抽取一张，那么第二次取出的数字能够整除第一次取出的数字的概率是多少？
1 2 3 4 5 6
1 (1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
2 (2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
3 (3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
4 (4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
5 (5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
6 (6,1) (6,2) (6,3) (6,4) (6,5) (6,6)
二
一
解: 列出所有可能的结果：
P(第二次取出的数字能够整除第一次取出的数字)=
2、有两把不同的锁和三把钥匙，其中两把钥匙恰好能分别打开这两把锁，第三把钥匙不能打开这两把锁。任意取一把钥匙去开任意一把锁，一次打开锁的概率是多少？
c
b
B
A
B
A
a
B
A
解: 设有A,B两把锁和a,b,c三把钥匙,其中钥匙a,b分别
可以打开锁A,B.列出所有可能的结果如下:
P(一次打开锁)= =
3、一次联欢晚会上，规定每个同学同时转动两个转盘(每个转盘被分成二等分和三等分)，若停止后指针所指的数字之和为奇数，则这个同学要表演唱歌节目；若数字之和为偶数，则要表演其他节目。试求这个同学表演唱歌节目的概率。你有几种方法？
1
2
3
1
2
4、某班要派出一对男女混合双打选手参加学校的乒乓球比赛，准备在小娟、小敏、小华三名女选手和小明、小强两名男选手中选男、女选手各一名组成一对参赛，一共能够组成哪几对？采用随机抽签的办法，恰好选出小敏和小强参赛的概率是多少？
4、有甲、乙两把不同的锁，各配有2把钥匙。求从这4把
钥匙中任取2把，能打开甲、乙两锁的概率。
B1
A2
B2
A2
B2
A1
A1
B2
A1
B2
B1
A1
A2
A2
B1
B1
解:设有A1,A2，B1, B2四把钥匙,其中钥匙A1,A2可以打开锁甲,B1, B2可以打开锁乙.列出所有可能的结果如下:
P(能打开甲、乙两锁)= =
钥匙1
钥匙2