课时分层作业26 函数的应用(一)-【新教材】人教B版(2019)高中数学必修第一册检测(Word含答案解析)
文档属性
| 名称 | 课时分层作业26 函数的应用(一)-【新教材】人教B版(2019)高中数学必修第一册检测(Word含答案解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 342.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-18 00:00:00 | ||
图片预览




文档简介
课时分层作业(二十六) 函数的应用(一)
(建议用时:40分钟)
一、选择题
1.某厂日产手套的总成本y(元)与日产量x(双)之间的关系为y=5x+40
000.而手套出厂价格为每双10元,要使该厂不亏本至少日产手套( )
A.2
000双
B.4
000双
C.6
000双
D.8
000双
2.某公司市场营销人员的个人月收入与其每月的销售量成一次函数关系,其图像如下图所示,由图中给出的信息可知,营销人员没有销售量时的收入是( )
A.310元
B.300元
C.290元
D.280元
3.某公司招聘员工,面试人数按拟录用人数分段计算,计算公式为:
y=
其中,x代表拟录用人数,y代表面试人数.若应聘的面试人数为60,则该公司拟录用人数为( )
A.15
B.40
C.25
D.130
4.某沙漠地区的某时段气温与时间的函数关系满足f(t)=-t2+24t-101(4≤t≤18),则该沙漠地区在该时段的最大温差是( )
A.54
B.58
C.64
D.68
5.一个人以6
m/s的速度去追停在交通灯前的汽车,当他离汽车25
m时,交通灯由红变绿,汽车以1
m/s2的加速度匀加速开走,那么( )
A.此人可在7
s内追上汽车
B.此人可在10
s内追上汽车
C.此人追不上汽车,其间距最少为5
m
D.此人追不上汽车,其间距最少为7
m
二、填空题
6.经市场调查,某商品的日销售量(单位:件)和价格(单位:元/件)均为时间t(单位:天)的函数.日销售量为f(t)=2t+100,价格为g(t)=t+4,则该种商品的日销售额S(单位:元)与时间t的函数解析式为________.
7.把长为12
cm的细铁丝截成两段,各自围成一个正三角形,那么这两个正三角形面积之和的最小值是________cm2.
8.国家规定个人稿费纳税办法为:不超过800元的不纳税;超过800元而不超过4
000元的按超出800元部分的14%纳税;超过4
000元的按全稿酬的11.2%纳税.某人出版了一本书共纳税420元,这个人的稿费为________元.
三、解答题
9.10辆货车从A站匀速驶往相距2
000千米的B站,其时速都是v千米/时,为安全起见,要求:每辆货车时速不得超过100千米/时,每辆货车间隔kv2千米(k为常数,货车长度忽略不计).将第一辆货车由A站出发到最后一辆货车到达B站所需时间t表示为v的函数f(v).
(1)求函数t=f(v),并写出v的取值范围.
(2)若k=,请问当v取何值时,t有最小值?并求出最小值.
10.一块形状为直角三角形的铁皮,直角边长分别是40
cm与60
cm,现在将它剪成一个矩形,并以此三角形的直角为矩形的一个角,问怎样剪才能使剩下的残料最少?并求出此时残料的面积.
11.在股票买卖过程中,经常用两种曲线来描述价格变化情况:一种是即时价格曲线y=f(x),另一种是平均价格曲线y=g(x),如f(2)=3表示股票开始买卖后2小时的即时价格为3元;g(2)=3表示2小时内的平均价格为3元.下面给出了四个图像,实线表示y=f(x),虚线表示y=g(x),其中可能正确的是( )
12.汽车的“燃油效率”是指汽车每消耗1
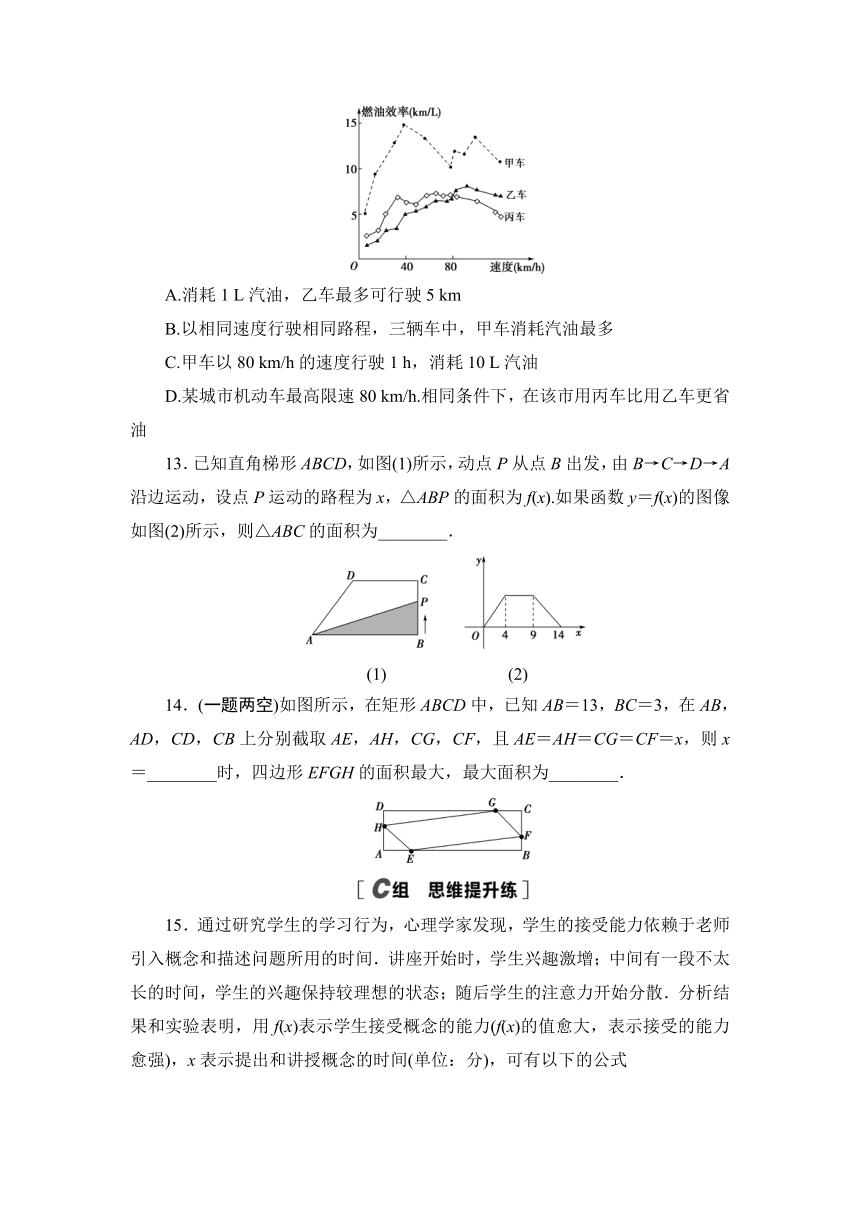
L汽油行驶的里程,下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况.下列叙述中正确的是( )
A.消耗1
L汽油,乙车最多可行驶5
km
B.以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
C.甲车以80
km/h的速度行驶1
h,消耗10
L汽油
D.某城市机动车最高限速80
km/h.相同条件下,在该市用丙车比用乙车更省油
13.已知直角梯形ABCD,如图(1)所示,动点P从点B出发,由B→C→D→A沿边运动,设点P运动的路程为x,△ABP的面积为f(x).如果函数y=f(x)的图像如图(2)所示,则△ABC的面积为________.
(1) (2)
14.(一题两空)如图所示,在矩形ABCD中,已知AB=13,BC=3,在AB,AD,CD,CB上分别截取AE,AH,CG,CF,且AE=AH=CG=CF=x,则x=________时,四边形EFGH的面积最大,最大面积为________.
15.通过研究学生的学习行为,心理学家发现,学生的接受能力依赖于老师引入概念和描述问题所用的时间.讲座开始时,学生兴趣激增;中间有一段不太长的时间,学生的兴趣保持较理想的状态;随后学生的注意力开始分散.分析结果和实验表明,用f(x)表示学生接受概念的能力(f(x)的值愈大,表示接受的能力愈强),x表示提出和讲授概念的时间(单位:分),可有以下的公式
f(x)=
(1)开讲后多少分钟,学生的接受能力最强?能维持多长时间?
(2)开讲后5分钟与开讲后20分钟比较,学生的接受能力何时强一些?
课时分层作业(二十六) 函数的应用(一)
(建议用时:40分钟)
一、选择题
1.某厂日产手套的总成本y(元)与日产量x(双)之间的关系为y=5x+40
000.而手套出厂价格为每双10元,要使该厂不亏本至少日产手套( )
A.2
000双
B.4
000双
C.6
000双
D.8
000双
D [由5x+40
000≤10x,得x≥8
000,即日产手套至少8
000双才不亏本.]
2.某公司市场营销人员的个人月收入与其每月的销售量成一次函数关系,其图像如下图所示,由图中给出的信息可知,营销人员没有销售量时的收入是( )
A.310元
B.300元
C.290元
D.280元
B [设函数解析式为y=kx+b(k≠0),
函数图像过点(1,800),(2,1
300),
则解得
∴y=500x+300,当x=0时,y=300.
∴营销人员没有销售量时的收入是300元.]
3.某公司招聘员工,面试人数按拟录用人数分段计算,计算公式为:
y=
其中,x代表拟录用人数,y代表面试人数.若应聘的面试人数为60,则该公司拟录用人数为( )
A.15
B.40
C.25
D.130
C [令y=60.
若4x=60,则x=15>10,不合题意;
若2x+10=60,则x=25,满足题意;
若1.5x=60,则x=40<100,不合题意.
故拟录用25人.]
4.某沙漠地区的某时段气温与时间的函数关系满足f(t)=-t2+24t-101(4≤t≤18),则该沙漠地区在该时段的最大温差是( )
A.54
B.58
C.64
D.68
C [函数f(t)=-t2+24t-101的图像的对称轴为直线t=12,所以f(t)在[4,12]递增,在[12,18]递减,所以f(t)max=f(12)=43,f(t)min=f(4)=-21,所以在该时段的最大温差是43-(-21)=64.]
5.一个人以6
m/s的速度去追停在交通灯前的汽车,当他离汽车25
m时,交通灯由红变绿,汽车以1
m/s2的加速度匀加速开走,那么( )
A.此人可在7
s内追上汽车
B.此人可在10
s内追上汽车
C.此人追不上汽车,其间距最少为5
m
D.此人追不上汽车,其间距最少为7
m
D [设汽车经过t
s行驶的路程为s
m,则s=t2,车与人的间距d=(s+25)-6t=t2-6t+25=(t-6)2+7.当t=6时,d取得最小值7.]
二、填空题
6.经市场调查,某商品的日销售量(单位:件)和价格(单位:元/件)均为时间t(单位:天)的函数.日销售量为f(t)=2t+100,价格为g(t)=t+4,则该种商品的日销售额S(单位:元)与时间t的函数解析式为________.
S(t)=2t2+108t+400,t∈N [日销售额=日销售量×价格,故S=f(t)×g(t)=(2t+100)×(t+4)=2t2+108t+400,t∈N.]
7.把长为12
cm的细铁丝截成两段,各自围成一个正三角形,那么这两个正三角形面积之和的最小值是________cm2.
2 [设一个三角形的边长为x
cm,则另一个三角形的边长为(4-x)cm,两个三角形的面积和为S=x2+(4-x)2=(x-2)2+2≥2,
这两个正三角形面积之和的最小值是2
cm2.]
8.国家规定个人稿费纳税办法为:不超过800元的不纳税;超过800元而不超过4
000元的按超出800元部分的14%纳税;超过4
000元的按全稿酬的11.2%纳税.某人出版了一本书共纳税420元,这个人的稿费为________元.
3
800 [若这个人的稿费为4
000元时,应纳税(4
000-800)×14%=448(元).
又∵420<448,∴此人的稿费应在800到4
000之间,设为x,∴(x-800)×14%=420,解得x=3
800元.]
三、解答题
9.10辆货车从A站匀速驶往相距2
000千米的B站,其时速都是v千米/时,为安全起见,要求:每辆货车时速不得超过100千米/时,每辆货车间隔kv2千米(k为常数,货车长度忽略不计).将第一辆货车由A站出发到最后一辆货车到达B站所需时间t表示为v的函数f(v).
(1)求函数t=f(v),并写出v的取值范围.
(2)若k=,请问当v取何值时,t有最小值?并求出最小值.
[解] (1)由题意,可得t=f(v)=,0<v≤100.
(2)由k=,可得t=+=.
又0<v≤100,所以由均值不等式得t≥×2=,
当且仅当v=,即v=60时等号成立.
故tmin=f(60)=.
所以当v=60千米/时时,t取得最小值,最小值为小时.
10.一块形状为直角三角形的铁皮,直角边长分别是40
cm与60
cm,现在将它剪成一个矩形,并以此三角形的直角为矩形的一个角,问怎样剪才能使剩下的残料最少?并求出此时残料的面积.
[解] 设直角三角形为△ABC,AC=40,BC=60,矩形为CDEF,如图所示,设CD=x,CF=y,则由Rt△AFE∽Rt△EDB得=,即=,解得y=40-x,
记剩下的残料面积为S,则
S=×60×40-xy=x2-40x+1
200=(x-30)2+600(0<x<60),
故当x=30时,Smin=600,此时y=20,
所以当x=30,y=20时,剩下的残料面积最少为600
cm2.
11.在股票买卖过程中,经常用两种曲线来描述价格变化情况:一种是即时价格曲线y=f(x),另一种是平均价格曲线y=g(x),如f(2)=3表示股票开始买卖后2小时的即时价格为3元;g(2)=3表示2小时内的平均价格为3元.下面给出了四个图像,实线表示y=f(x),虚线表示y=g(x),其中可能正确的是( )
C [根据即时价格与平均价格的相互依赖关系,可知,当即时价格升高时,对应平均价格也升高;反之,当即时价格降低时,对应平均价格也降低,故选项C中的图像可能正确.]
12.汽车的“燃油效率”是指汽车每消耗1
L汽油行驶的里程,下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况.下列叙述中正确的是( )
A.消耗1
L汽油,乙车最多可行驶5
km
B.以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
C.甲车以80
km/h的速度行驶1
h,消耗10
L汽油
D.某城市机动车最高限速80
km/h.相同条件下,在该市用丙车比用乙车更省油
D [对于A选项,由题图可知,当乙车速度大于40
km/h时,乙车每消耗1
L汽油,行驶里程都超过5
km,则A错;
对于B选项,由题意可知,以相同速度行驶相同路程,燃油效率越高,耗油越少,故三辆车中甲车耗油最少,则B错;
对于C选项,甲车以80
km/h的速度行驶时,燃油效率为10
km/L,则行驶1
h,消耗了汽油80×1÷10=8(L),则C错;
对于D选项,当行驶速度小于80
km/h时,在相同条件下,丙车的燃油效率高于乙车,则在该市用丙车比用乙车更省油,则D对.
综上,选D.]
13.已知直角梯形ABCD,如图(1)所示,动点P从点B出发,由B→C→D→A沿边运动,设点P运动的路程为x,△ABP的面积为f(x).如果函数y=f(x)的图像如图(2)所示,则△ABC的面积为________.
(1) (2)
16 [由题图可知BC=4,CD=5,DA=5,
所以AB=5+=5+3=8.
所以S△ABC=×8×4=16.]
14.(一题两空)如图所示,在矩形ABCD中,已知AB=13,BC=3,在AB,AD,CD,CB上分别截取AE,AH,CG,CF,且AE=AH=CG=CF=x,则x=________时,四边形EFGH的面积最大,最大面积为________.
3 30 [设四边形EFGH的面积为S,则
S=13×3-2
=-2x2+16x=-2(x-4)2+32,x∈(0,3].
因为S=-2(x-4)2+32在(0,3]上是增函数,
所以当x=3时,S有最大值为30.]
15.通过研究学生的学习行为,心理学家发现,学生的接受能力依赖于老师引入概念和描述问题所用的时间.讲座开始时,学生兴趣激增;中间有一段不太长的时间,学生的兴趣保持较理想的状态;随后学生的注意力开始分散.分析结果和实验表明,用f(x)表示学生接受概念的能力(f(x)的值愈大,表示接受的能力愈强),x表示提出和讲授概念的时间(单位:分),可有以下的公式
f(x)=
(1)开讲后多少分钟,学生的接受能力最强?能维持多长时间?
(2)开讲后5分钟与开讲后20分钟比较,学生的接受能力何时强一些?
[解] (1)当0由f(x)的图像(图略)可知,当x=10时,
f(x)max=f(10)=59;当10当16因此,开讲后10分钟,学生的接受能力最强,并能持续6分钟.
(2)∵f(5)=-0.1×(5-13)2+59.9=53.5,
f(20)=-3×20+107=47<53.5,
∴开讲后5分钟学生的接受能力比开讲后20分钟强.
(建议用时:40分钟)
一、选择题
1.某厂日产手套的总成本y(元)与日产量x(双)之间的关系为y=5x+40
000.而手套出厂价格为每双10元,要使该厂不亏本至少日产手套( )
A.2
000双
B.4
000双
C.6
000双
D.8
000双
2.某公司市场营销人员的个人月收入与其每月的销售量成一次函数关系,其图像如下图所示,由图中给出的信息可知,营销人员没有销售量时的收入是( )
A.310元
B.300元
C.290元
D.280元
3.某公司招聘员工,面试人数按拟录用人数分段计算,计算公式为:
y=
其中,x代表拟录用人数,y代表面试人数.若应聘的面试人数为60,则该公司拟录用人数为( )
A.15
B.40
C.25
D.130
4.某沙漠地区的某时段气温与时间的函数关系满足f(t)=-t2+24t-101(4≤t≤18),则该沙漠地区在该时段的最大温差是( )
A.54
B.58
C.64
D.68
5.一个人以6
m/s的速度去追停在交通灯前的汽车,当他离汽车25
m时,交通灯由红变绿,汽车以1
m/s2的加速度匀加速开走,那么( )
A.此人可在7
s内追上汽车
B.此人可在10
s内追上汽车
C.此人追不上汽车,其间距最少为5
m
D.此人追不上汽车,其间距最少为7
m
二、填空题
6.经市场调查,某商品的日销售量(单位:件)和价格(单位:元/件)均为时间t(单位:天)的函数.日销售量为f(t)=2t+100,价格为g(t)=t+4,则该种商品的日销售额S(单位:元)与时间t的函数解析式为________.
7.把长为12
cm的细铁丝截成两段,各自围成一个正三角形,那么这两个正三角形面积之和的最小值是________cm2.
8.国家规定个人稿费纳税办法为:不超过800元的不纳税;超过800元而不超过4
000元的按超出800元部分的14%纳税;超过4
000元的按全稿酬的11.2%纳税.某人出版了一本书共纳税420元,这个人的稿费为________元.
三、解答题
9.10辆货车从A站匀速驶往相距2
000千米的B站,其时速都是v千米/时,为安全起见,要求:每辆货车时速不得超过100千米/时,每辆货车间隔kv2千米(k为常数,货车长度忽略不计).将第一辆货车由A站出发到最后一辆货车到达B站所需时间t表示为v的函数f(v).
(1)求函数t=f(v),并写出v的取值范围.
(2)若k=,请问当v取何值时,t有最小值?并求出最小值.
10.一块形状为直角三角形的铁皮,直角边长分别是40
cm与60
cm,现在将它剪成一个矩形,并以此三角形的直角为矩形的一个角,问怎样剪才能使剩下的残料最少?并求出此时残料的面积.
11.在股票买卖过程中,经常用两种曲线来描述价格变化情况:一种是即时价格曲线y=f(x),另一种是平均价格曲线y=g(x),如f(2)=3表示股票开始买卖后2小时的即时价格为3元;g(2)=3表示2小时内的平均价格为3元.下面给出了四个图像,实线表示y=f(x),虚线表示y=g(x),其中可能正确的是( )
12.汽车的“燃油效率”是指汽车每消耗1
L汽油行驶的里程,下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况.下列叙述中正确的是( )
A.消耗1
L汽油,乙车最多可行驶5
km
B.以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
C.甲车以80
km/h的速度行驶1
h,消耗10
L汽油
D.某城市机动车最高限速80
km/h.相同条件下,在该市用丙车比用乙车更省油
13.已知直角梯形ABCD,如图(1)所示,动点P从点B出发,由B→C→D→A沿边运动,设点P运动的路程为x,△ABP的面积为f(x).如果函数y=f(x)的图像如图(2)所示,则△ABC的面积为________.
(1) (2)
14.(一题两空)如图所示,在矩形ABCD中,已知AB=13,BC=3,在AB,AD,CD,CB上分别截取AE,AH,CG,CF,且AE=AH=CG=CF=x,则x=________时,四边形EFGH的面积最大,最大面积为________.
15.通过研究学生的学习行为,心理学家发现,学生的接受能力依赖于老师引入概念和描述问题所用的时间.讲座开始时,学生兴趣激增;中间有一段不太长的时间,学生的兴趣保持较理想的状态;随后学生的注意力开始分散.分析结果和实验表明,用f(x)表示学生接受概念的能力(f(x)的值愈大,表示接受的能力愈强),x表示提出和讲授概念的时间(单位:分),可有以下的公式
f(x)=
(1)开讲后多少分钟,学生的接受能力最强?能维持多长时间?
(2)开讲后5分钟与开讲后20分钟比较,学生的接受能力何时强一些?
课时分层作业(二十六) 函数的应用(一)
(建议用时:40分钟)
一、选择题
1.某厂日产手套的总成本y(元)与日产量x(双)之间的关系为y=5x+40
000.而手套出厂价格为每双10元,要使该厂不亏本至少日产手套( )
A.2
000双
B.4
000双
C.6
000双
D.8
000双
D [由5x+40
000≤10x,得x≥8
000,即日产手套至少8
000双才不亏本.]
2.某公司市场营销人员的个人月收入与其每月的销售量成一次函数关系,其图像如下图所示,由图中给出的信息可知,营销人员没有销售量时的收入是( )
A.310元
B.300元
C.290元
D.280元
B [设函数解析式为y=kx+b(k≠0),
函数图像过点(1,800),(2,1
300),
则解得
∴y=500x+300,当x=0时,y=300.
∴营销人员没有销售量时的收入是300元.]
3.某公司招聘员工,面试人数按拟录用人数分段计算,计算公式为:
y=
其中,x代表拟录用人数,y代表面试人数.若应聘的面试人数为60,则该公司拟录用人数为( )
A.15
B.40
C.25
D.130
C [令y=60.
若4x=60,则x=15>10,不合题意;
若2x+10=60,则x=25,满足题意;
若1.5x=60,则x=40<100,不合题意.
故拟录用25人.]
4.某沙漠地区的某时段气温与时间的函数关系满足f(t)=-t2+24t-101(4≤t≤18),则该沙漠地区在该时段的最大温差是( )
A.54
B.58
C.64
D.68
C [函数f(t)=-t2+24t-101的图像的对称轴为直线t=12,所以f(t)在[4,12]递增,在[12,18]递减,所以f(t)max=f(12)=43,f(t)min=f(4)=-21,所以在该时段的最大温差是43-(-21)=64.]
5.一个人以6
m/s的速度去追停在交通灯前的汽车,当他离汽车25
m时,交通灯由红变绿,汽车以1
m/s2的加速度匀加速开走,那么( )
A.此人可在7
s内追上汽车
B.此人可在10
s内追上汽车
C.此人追不上汽车,其间距最少为5
m
D.此人追不上汽车,其间距最少为7
m
D [设汽车经过t
s行驶的路程为s
m,则s=t2,车与人的间距d=(s+25)-6t=t2-6t+25=(t-6)2+7.当t=6时,d取得最小值7.]
二、填空题
6.经市场调查,某商品的日销售量(单位:件)和价格(单位:元/件)均为时间t(单位:天)的函数.日销售量为f(t)=2t+100,价格为g(t)=t+4,则该种商品的日销售额S(单位:元)与时间t的函数解析式为________.
S(t)=2t2+108t+400,t∈N [日销售额=日销售量×价格,故S=f(t)×g(t)=(2t+100)×(t+4)=2t2+108t+400,t∈N.]
7.把长为12
cm的细铁丝截成两段,各自围成一个正三角形,那么这两个正三角形面积之和的最小值是________cm2.
2 [设一个三角形的边长为x
cm,则另一个三角形的边长为(4-x)cm,两个三角形的面积和为S=x2+(4-x)2=(x-2)2+2≥2,
这两个正三角形面积之和的最小值是2
cm2.]
8.国家规定个人稿费纳税办法为:不超过800元的不纳税;超过800元而不超过4
000元的按超出800元部分的14%纳税;超过4
000元的按全稿酬的11.2%纳税.某人出版了一本书共纳税420元,这个人的稿费为________元.
3
800 [若这个人的稿费为4
000元时,应纳税(4
000-800)×14%=448(元).
又∵420<448,∴此人的稿费应在800到4
000之间,设为x,∴(x-800)×14%=420,解得x=3
800元.]
三、解答题
9.10辆货车从A站匀速驶往相距2
000千米的B站,其时速都是v千米/时,为安全起见,要求:每辆货车时速不得超过100千米/时,每辆货车间隔kv2千米(k为常数,货车长度忽略不计).将第一辆货车由A站出发到最后一辆货车到达B站所需时间t表示为v的函数f(v).
(1)求函数t=f(v),并写出v的取值范围.
(2)若k=,请问当v取何值时,t有最小值?并求出最小值.
[解] (1)由题意,可得t=f(v)=,0<v≤100.
(2)由k=,可得t=+=.
又0<v≤100,所以由均值不等式得t≥×2=,
当且仅当v=,即v=60时等号成立.
故tmin=f(60)=.
所以当v=60千米/时时,t取得最小值,最小值为小时.
10.一块形状为直角三角形的铁皮,直角边长分别是40
cm与60
cm,现在将它剪成一个矩形,并以此三角形的直角为矩形的一个角,问怎样剪才能使剩下的残料最少?并求出此时残料的面积.
[解] 设直角三角形为△ABC,AC=40,BC=60,矩形为CDEF,如图所示,设CD=x,CF=y,则由Rt△AFE∽Rt△EDB得=,即=,解得y=40-x,
记剩下的残料面积为S,则
S=×60×40-xy=x2-40x+1
200=(x-30)2+600(0<x<60),
故当x=30时,Smin=600,此时y=20,
所以当x=30,y=20时,剩下的残料面积最少为600
cm2.
11.在股票买卖过程中,经常用两种曲线来描述价格变化情况:一种是即时价格曲线y=f(x),另一种是平均价格曲线y=g(x),如f(2)=3表示股票开始买卖后2小时的即时价格为3元;g(2)=3表示2小时内的平均价格为3元.下面给出了四个图像,实线表示y=f(x),虚线表示y=g(x),其中可能正确的是( )
C [根据即时价格与平均价格的相互依赖关系,可知,当即时价格升高时,对应平均价格也升高;反之,当即时价格降低时,对应平均价格也降低,故选项C中的图像可能正确.]
12.汽车的“燃油效率”是指汽车每消耗1
L汽油行驶的里程,下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况.下列叙述中正确的是( )
A.消耗1
L汽油,乙车最多可行驶5
km
B.以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
C.甲车以80
km/h的速度行驶1
h,消耗10
L汽油
D.某城市机动车最高限速80
km/h.相同条件下,在该市用丙车比用乙车更省油
D [对于A选项,由题图可知,当乙车速度大于40
km/h时,乙车每消耗1
L汽油,行驶里程都超过5
km,则A错;
对于B选项,由题意可知,以相同速度行驶相同路程,燃油效率越高,耗油越少,故三辆车中甲车耗油最少,则B错;
对于C选项,甲车以80
km/h的速度行驶时,燃油效率为10
km/L,则行驶1
h,消耗了汽油80×1÷10=8(L),则C错;
对于D选项,当行驶速度小于80
km/h时,在相同条件下,丙车的燃油效率高于乙车,则在该市用丙车比用乙车更省油,则D对.
综上,选D.]
13.已知直角梯形ABCD,如图(1)所示,动点P从点B出发,由B→C→D→A沿边运动,设点P运动的路程为x,△ABP的面积为f(x).如果函数y=f(x)的图像如图(2)所示,则△ABC的面积为________.
(1) (2)
16 [由题图可知BC=4,CD=5,DA=5,
所以AB=5+=5+3=8.
所以S△ABC=×8×4=16.]
14.(一题两空)如图所示,在矩形ABCD中,已知AB=13,BC=3,在AB,AD,CD,CB上分别截取AE,AH,CG,CF,且AE=AH=CG=CF=x,则x=________时,四边形EFGH的面积最大,最大面积为________.
3 30 [设四边形EFGH的面积为S,则
S=13×3-2
=-2x2+16x=-2(x-4)2+32,x∈(0,3].
因为S=-2(x-4)2+32在(0,3]上是增函数,
所以当x=3时,S有最大值为30.]
15.通过研究学生的学习行为,心理学家发现,学生的接受能力依赖于老师引入概念和描述问题所用的时间.讲座开始时,学生兴趣激增;中间有一段不太长的时间,学生的兴趣保持较理想的状态;随后学生的注意力开始分散.分析结果和实验表明,用f(x)表示学生接受概念的能力(f(x)的值愈大,表示接受的能力愈强),x表示提出和讲授概念的时间(单位:分),可有以下的公式
f(x)=
(1)开讲后多少分钟,学生的接受能力最强?能维持多长时间?
(2)开讲后5分钟与开讲后20分钟比较,学生的接受能力何时强一些?
[解] (1)当0
f(x)max=f(10)=59;当10
(2)∵f(5)=-0.1×(5-13)2+59.9=53.5,
f(20)=-3×20+107=47<53.5,
∴开讲后5分钟学生的接受能力比开讲后20分钟强.
