2020-2021学年河北省唐山市遵化市七年级(下)期末数学试卷(Word版 含解析)
文档属性
| 名称 | 2020-2021学年河北省唐山市遵化市七年级(下)期末数学试卷(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 560.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-18 07:30:48 | ||
图片预览



文档简介
2020-2021学年河北省唐山市遵化市七年级(下)期末数学试卷
一、选择题(共42分。1-10每小题3分,11-16每小题3分).
1.计算:20( )
A.2
B.﹣2
C.1
D.﹣1
2.已知二元一次方程3x+2y=11,则( )
A.任何一对有理数都是它的解
B.只有一个解
C.只有两个解
D.有无数个解
3.如图,能判定EB∥AC的条件是( )
A.∠C=∠ABE
B.∠A=∠EBD
C.∠C=∠DBE
D.∠A=∠ABC
4.下列运算正确的是( )
A.x2+x=x3
B.2﹣1=﹣2
C.(x3)2÷x2=x4
D.(﹣m2)2=﹣m4
5.已知,a,b两个实数在数轴上的对应点如图所示,则下列各式一定成立的是( )
A.a﹣1>b﹣1
B.3a>3b
C.﹣a>﹣b
D.a+b>a﹣b
6.如果多项式x2+mx+16是一个完全平方式,则m的值是( )
A.±4
B.4
C.8
D.±8
7.下列从左到右的变形,是因式分解的是( )
A.(3﹣x)(3+x)=9﹣x2
B.(y+1)(y﹣3)=(3﹣y)(y+1)
C.4yz﹣2y2z+z=2y(2z﹣zy)+z
D.﹣8x2+8x﹣2=﹣2(2x﹣1)2
8.若关于x的不等式组恰有3个整数解,则字母a的取值范围是( )
A.a≤﹣1
B.﹣2≤a<﹣1
C.a<﹣1
D.﹣2<a≤﹣1
9.用加减法解方程组下列解法不正确的是( )
A.①×2﹣②×(﹣3),消去y
B.①×2﹣②×3,消去y
C.①×(﹣3)+②×2,消去x
D.①×3﹣②×2,消去x
10.下列长度的三条线段,能组成三角形的是( )
A.1,2,4
B.2,2,4
C.2,3,6
D.3,4,5
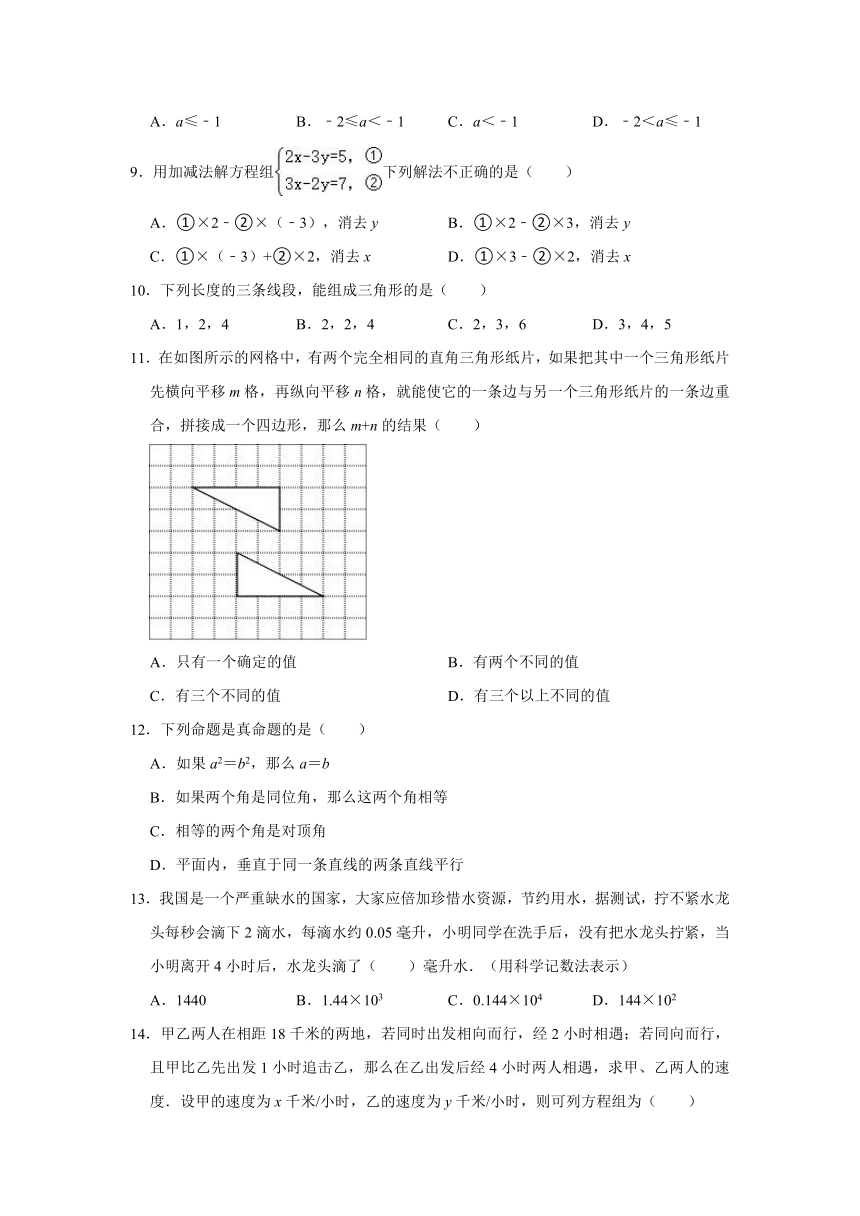
11.在如图所示的网格中,有两个完全相同的直角三角形纸片,如果把其中一个三角形纸片先横向平移m格,再纵向平移n格,就能使它的一条边与另一个三角形纸片的一条边重合,拼接成一个四边形,那么m+n的结果( )
A.只有一个确定的值
B.有两个不同的值
C.有三个不同的值
D.有三个以上不同的值
12.下列命题是真命题的是( )
A.如果a2=b2,那么a=b
B.如果两个角是同位角,那么这两个角相等
C.相等的两个角是对顶角
D.平面内,垂直于同一条直线的两条直线平行
13.我国是一个严重缺水的国家,大家应倍加珍惜水资源,节约用水,据测试,拧不紧水龙头每秒会滴下2滴水,每滴水约0.05毫升,小明同学在洗手后,没有把水龙头拧紧,当小明离开4小时后,水龙头滴了( )毫升水.(用科学记数法表示)
A.1440
B.1.44×103
C.0.144×104
D.144×102
14.甲乙两人在相距18千米的两地,若同时出发相向而行,经2小时相遇;若同向而行,且甲比乙先出发1小时追击乙,那么在乙出发后经4小时两人相遇,求甲、乙两人的速度.设甲的速度为x千米/小时,乙的速度为y千米/小时,则可列方程组为( )
A.
B.
C.
D.
15.利用尺规作图,作△ABC边上的高AD,正确的是( )
A.
B.
C.
D.
16.我们所学的多项式因分解的方法主要有:①提公因式法;②平方差公式法;③完全平方公式法.现将多项式(x﹣y)3+4(y﹣x)进行因式分解,使用的方法有( )
A.①②
B.①③
C.②③
D.①②③
二、填空题(本大题有3个小题,共9分。每小题3分,把答案写在题中横线上)
17.一元一次不等式5x+10≥0的负整数解是
.
18.已知三角形的一个内角α是另一个内角β的两倍,当α=80°时,这个三角形的最小内角是
.
19.若a+b=2,ab=﹣3,则代数式a3b+2a2b2+ab3的值为
.
三、解答题(本大题有7个小题,共69分,解答应写出必要的文字说明、证明过程或演算步骤)。
20.已知是方程2x﹣ay=9的一个解,解决下列问题:
(1)求a的值;
(2)化简并求值:(a﹣1)(a+1)﹣2(a﹣1)2+a(a﹣3).
21.如图,DE⊥BC,AF⊥BC,∠1+∠2=180°.
求证:∠FGA+∠CAB=180°
22.某校学生社会实践小组开展调查,获取了本校食堂学生早餐的营养情况,如图是调查报告中的一部分,根据所得信息,解答下列问题.
调查报告1.早餐总质量为500g;2.早餐的成分是蛋白质、脂肪、矿物质和碳水化合物;3.所含蛋白质的质量与矿物质之比为4:1;4.脂肪占早餐总质量的10%.
(1)早餐中所含脂肪的质量是
g.
(2)若早餐中蛋白质和碳水化合物所占百分比的和不高于85%,求早餐中所含碳水化合物质量的最大值.
23.如图,在△ABC中,∠B=40°,∠C=70°,AD是△ABC的角平分线,点E在BD上,点F在CA的延长线上,EF∥AD,求∠F的度数.
24.已知关于x、y的二元一次方程组.
(1)若m=1,求方程组的解;
(2)若方程组的解中,x的值为正数,y的值为负数,求m的范围.
25.如图所示,在△ABC中,BO、CO是角平分线.
(1)∠ABC=50°,∠ACB=60°,求∠BOC的度数,并说明理由.
(2)题(1)中,如将“∠ABC=50°,∠ACB=60°”改为“∠A=70°”,求∠BOC的度数.
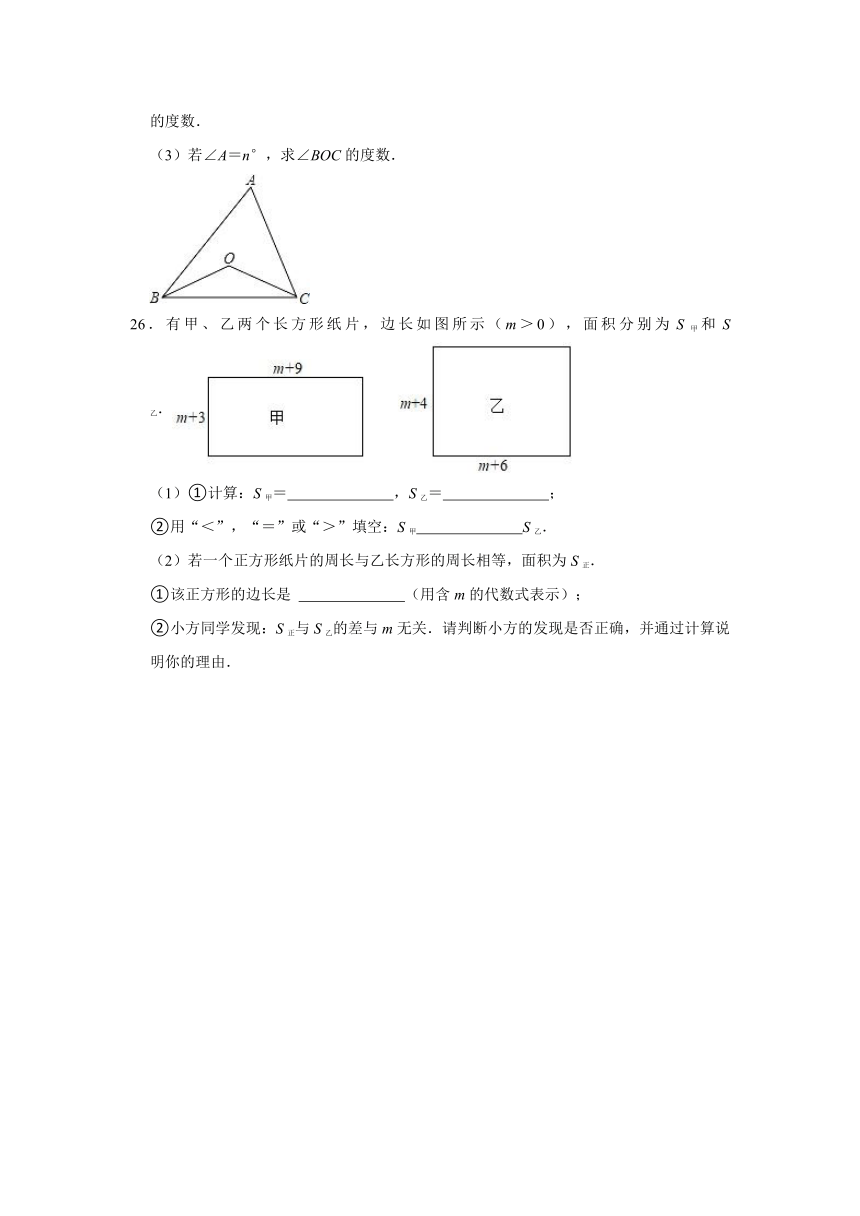
(3)若∠A=n°,求∠BOC的度数.
26.有甲、乙两个长方形纸片,边长如图所示(m>0),面积分别为S甲和S乙.
(1)①计算:S甲=
,S乙=
;
②用“<”,“=”或“>”填空:S甲
S乙.
(2)若一个正方形纸片的周长与乙长方形的周长相等,面积为S正.
①该正方形的边长是
(用含m的代数式表示);
②小方同学发现:S正与S乙的差与m无关.请判断小方的发现是否正确,并通过计算说明你的理由.
参考答案
一、选择题(本大题有16个小题,共42分。1-10每小题3分,11-16每小题3分。在每小题给出的四个选项中,只有一项符合题目要求)。
1.计算:20( )
A.2
B.﹣2
C.1
D.﹣1
【分析】根据零指数幂的意义即可求出答案.
解:原式=1,
故选:C.
2.已知二元一次方程3x+2y=11,则( )
A.任何一对有理数都是它的解
B.只有一个解
C.只有两个解
D.有无数个解
【分析】将二元一次方程3x+2y=11,化为用一个未知数表示另一个未知数的情况,即可解答.
解:原方程可化为y=,可见对于每一个x的值,y都有唯一的值和它相对应,故方程有无数个解.
故选:D.
3.如图,能判定EB∥AC的条件是( )
A.∠C=∠ABE
B.∠A=∠EBD
C.∠C=∠DBE
D.∠A=∠ABC
【分析】通过角相等判定两直线平行,则判断两角是否能推出同位角或内错角相等即可.
解:∵只有同位角相等,内错角相等,同旁内角互补才能判断两直线平行,
只有选项C中∠C=∠DBE是同位角相等,故能判定两直线平行,
故选:C.
4.下列运算正确的是( )
A.x2+x=x3
B.2﹣1=﹣2
C.(x3)2÷x2=x4
D.(﹣m2)2=﹣m4
【分析】根据合并同类项法则,负整数指数幂,幂的乘方和积的乘方,同底数幂的除法分别求出每个式子的值,再进行判断即可.
解:A、x2和x不能合并,故本选项不符合题意;
B、2﹣1=,故本选项不符合题意;
C、(x3)2÷x2=x4,故本选项符合题意;
D、(﹣m2)2=m4,故本选项不符合题意;
故选:C.
5.已知,a,b两个实数在数轴上的对应点如图所示,则下列各式一定成立的是( )
A.a﹣1>b﹣1
B.3a>3b
C.﹣a>﹣b
D.a+b>a﹣b
【分析】首先根据图示,可得a<b<0,然后根据不等式的性质,逐一判断出哪个式子一定成立即可.
解:根据图示,可得a<b<0,
∵a<b,
∴a﹣1<b﹣1,
∴选项A不正确;
∵a<b,
∴3a<3b,
∴选项B不正确;
∵a<b,
∴﹣a>﹣b,
∴选项C正确;
∵a<b<0,
∴b<﹣b,
∴a+b<a﹣b,
∴选项D不正确.
故选:C.
6.如果多项式x2+mx+16是一个完全平方式,则m的值是( )
A.±4
B.4
C.8
D.±8
【分析】根据完全平方公式有两个,则x2+mx+16=(x±4)2,展开即可求解;
解:∵完全平方公式有两个,
∴x2+mx+16=(x±4)2,
∴m=±8;
故选:D.
7.下列从左到右的变形,是因式分解的是( )
A.(3﹣x)(3+x)=9﹣x2
B.(y+1)(y﹣3)=(3﹣y)(y+1)
C.4yz﹣2y2z+z=2y(2z﹣zy)+z
D.﹣8x2+8x﹣2=﹣2(2x﹣1)2
【分析】分别利用因式分解的定义分析得出答案.
解:A、(3﹣x)(3+x)=9﹣x2,是整式的乘法运算,故此选项错误;
B、(y+1)(y﹣3)≠(3﹣y)(y+1),不符合因式分解的定义,故此选项错误;
C、4yz﹣2y2z+z=2y(2z﹣zy)+z,不符合因式分解的定义,故此选项错误;
D、﹣8x2+8x﹣2=﹣2(2x﹣1)2,正确.
故选:D.
8.若关于x的不等式组恰有3个整数解,则字母a的取值范围是( )
A.a≤﹣1
B.﹣2≤a<﹣1
C.a<﹣1
D.﹣2<a≤﹣1
【分析】先确定不等式组的整数解,再求出a的范围即可.
解:∵关于x的不等式组恰有3个整数解,
∴整数解为1,0,﹣1,
∴﹣2≤a<﹣1,
故选:B.
9.用加减法解方程组下列解法不正确的是( )
A.①×2﹣②×(﹣3),消去y
B.①×2﹣②×3,消去y
C.①×(﹣3)+②×2,消去x
D.①×3﹣②×2,消去x
【分析】方程组利用加减消元法变形,即可做出判断.
解:用加减法解方程组,可以①×2﹣②×3,消去y;①×(﹣3)+②×2,消去x;①×3﹣②×2,消去x,
故选:A.
10.下列长度的三条线段,能组成三角形的是( )
A.1,2,4
B.2,2,4
C.2,3,6
D.3,4,5
【分析】根据三角形的三边满足两边之和大于第三边来进行判断.
解:A、1+2<4,不能构成三角形,不符合题意;
B、2+2=4,不能构成三角形,不符合题意;
C、2+3<6,不能构成三角形,不符合题意;
D、3+4>5,能构成三角形,符合题意.
故选:D.
11.在如图所示的网格中,有两个完全相同的直角三角形纸片,如果把其中一个三角形纸片先横向平移m格,再纵向平移n格,就能使它的一条边与另一个三角形纸片的一条边重合,拼接成一个四边形,那么m+n的结果( )
A.只有一个确定的值
B.有两个不同的值
C.有三个不同的值
D.有三个以上不同的值
【分析】根据两个全等的直角三角形可以组成一个矩形或一个平行四边形可得出答案.
解:(1)当两斜边重合的时候可组成一个矩形,此时m=2,n=3,m+n=5;
(2)当两直角边重合时有两种情况,①短边重合,此时m=2,n=3,m+n=5;
②长边重合,此时m=2,n=5,m+n=7.
综上可得:m+n=5或7.
故选:B.
12.下列命题是真命题的是( )
A.如果a2=b2,那么a=b
B.如果两个角是同位角,那么这两个角相等
C.相等的两个角是对顶角
D.平面内,垂直于同一条直线的两条直线平行
【分析】利用平方的定义、平行线的性质、对顶角的性质及平面内两直线的位置关系分别判断后即可确定正确的选项.
解:A、如果a2=b2,那么a=±b,故错误,是假命题;
B、两直线平行,同位角才相等,故错误,是假命题;
C、相等的两个角不一定是对顶角,故错误,是假命题;
D、平面内,垂直于同一条直线的两条直线平行,正确,是真命题,
故选:D.
13.我国是一个严重缺水的国家,大家应倍加珍惜水资源,节约用水,据测试,拧不紧水龙头每秒会滴下2滴水,每滴水约0.05毫升,小明同学在洗手后,没有把水龙头拧紧,当小明离开4小时后,水龙头滴了( )毫升水.(用科学记数法表示)
A.1440
B.1.44×103
C.0.144×104
D.144×102
【分析】首先求出4小时滴的水量,再利用科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.
解:∵拧不紧水龙头每秒会滴下2滴水,每滴水约0.05毫升,小明同学在洗手后,没有把水龙头拧紧,
∴当小明离开4小时后,水龙头滴了2×0.05×4×60×60=1440(毫升),
将1440用科学记数法表示为:1.44×103.
故选:B.
14.甲乙两人在相距18千米的两地,若同时出发相向而行,经2小时相遇;若同向而行,且甲比乙先出发1小时追击乙,那么在乙出发后经4小时两人相遇,求甲、乙两人的速度.设甲的速度为x千米/小时,乙的速度为y千米/小时,则可列方程组为( )
A.
B.
C.
D.
【分析】根据题意可得等量关系:①甲2小时的路程+乙2小时的路程=18千米;②甲5小时的路程﹣乙4小时的路程=18千米,根据等量关系列出方程组即可.
解:设甲的速度为x千米/小时,乙的速度为y千米/小时,
由题意得:,
故选:B.
15.利用尺规作图,作△ABC边上的高AD,正确的是( )
A.
B.
C.
D.
【分析】过点A作BC的垂线,垂足为D,则AD即为所求.
解:过点A作BC的垂线,垂足为D,
故选:B.
16.我们所学的多项式因分解的方法主要有:①提公因式法;②平方差公式法;③完全平方公式法.现将多项式(x﹣y)3+4(y﹣x)进行因式分解,使用的方法有( )
A.①②
B.①③
C.②③
D.①②③
【分析】直接利用提取公因式法以及公式法分解因式得出答案.
解:(x﹣y)3+4(y﹣x)
=(x﹣y)3﹣4(x﹣y)
=(x﹣y)[(x﹣y)2﹣4]
=(x﹣y)(x﹣y+2)(x﹣y﹣2),
故将多项式(x﹣y)3+4(y﹣x)进行因式分解,使用的方法有:①提公因式法;②平方差公式法;
故选:A.
二、填空题(本大题有3个小题,共9分。每小题3分,把答案写在题中横线上)
17.一元一次不等式5x+10≥0的负整数解是
﹣1,﹣2 .
【分析】首先利用不等式的基本性质解不等式,再从不等式的解集中找出适合条件的负整数即可.
解:5x+10≥0,
∴5x≥﹣10,
∴x≥﹣2,
则不等式的负整数解为﹣1,﹣2,
故答案为﹣1,﹣2.
18.已知三角形的一个内角α是另一个内角β的两倍,当α=80°时,这个三角形的最小内角是
40° .
【分析】根据题意可以得到α=2β,当当α=80°时,求出β,再根据三角形内角和定理,求出最后一个角,进行大小比较,即可得到答案.
解:∵三角形的一个内角α是另一个内角β的两倍,
∴α=2β,
当α=80°时,
则β=40°,
∴三角形的最后一个内角为:180°﹣80°﹣40°=60°,
∵40°<60°<80°,
∴这个三角形的最小内角是40°,
故答案为:40°.
19.若a+b=2,ab=﹣3,则代数式a3b+2a2b2+ab3的值为 ﹣12 .
【分析】根据a3b+2a2b2+ab3=ab(a2+2ab+b2)=ab(a+b)2,结合已知数据即可求出代数式a3b+2a2b2+ab3的值.
解:∵a+b=2,ab=﹣3,
∴a3b+2a2b2+ab3=ab(a2+2ab+b2),
=ab(a+b)2,
=﹣3×4,
=﹣12.
故答案为:﹣12.
三、解答题(本大题有7个小题,共69分,解答应写出必要的文字说明、证明过程或演算步骤)。
20.已知是方程2x﹣ay=9的一个解,解决下列问题:
(1)求a的值;
(2)化简并求值:(a﹣1)(a+1)﹣2(a﹣1)2+a(a﹣3).
【分析】(1)把x、y的值代入方程可求得a的值;
(2)根据乘法公式先化简,再把a的值代入求值即可.
解:(1)∵是方程2x﹣ay=9的一个解,
∴6﹣a=9,解得a=﹣3;
(2)(a﹣1)(a+1)﹣2(a﹣1)2+a(a﹣3)
=a2﹣1﹣2(a2﹣2a+1)+a2﹣3a
=a2﹣1﹣2a2+4a﹣2+a2﹣3a
=a﹣3,
把a=﹣3代入上式可得:原式=﹣3﹣3=﹣6.
21.如图,DE⊥BC,AF⊥BC,∠1+∠2=180°.
求证:∠FGA+∠CAB=180°
【分析】证明AF∥DE,由平行线的性质得出∠2+∠3=180°,证出∠1=∠3,得出GF∥AC,由平行线的性质即可得出结论.
【解答】证明:∵DE⊥BC,AF⊥BC,
∴AF∥DE,
∴∠2+∠3=180°,
∵∠1+∠2=180°,
∴∠1=∠3,
∴GF∥AC,
∴∠FGA+∠CAB=180°.
22.某校学生社会实践小组开展调查,获取了本校食堂学生早餐的营养情况,如图是调查报告中的一部分,根据所得信息,解答下列问题.
调查报告1.早餐总质量为500g;2.早餐的成分是蛋白质、脂肪、矿物质和碳水化合物;3.所含蛋白质的质量与矿物质之比为4:1;4.脂肪占早餐总质量的10%.
(1)早餐中所含脂肪的质量是
50 g.
(2)若早餐中蛋白质和碳水化合物所占百分比的和不高于85%,求早餐中所含碳水化合物质量的最大值.
【分析】(1)根据脂肪所占的百分比结合这份快餐的总质量,即可求出结论;
(2)设所含矿物质的质量为xg,则所含蛋白质的质量为4xg,所含碳水化合物的质量为(500﹣50﹣4x﹣x)g,由这份快餐中蛋白质和碳水化合物所占百分比的和不高于85%,即可得出关于x的一元一次不等式,解之取其其中的最小值即可得出结论.
解:(1)500×10%=50(g).
∴这份快餐中所含脂肪质量为50g.
故答案为50;
(2)设所含矿物质的质量为xg,则所含蛋白质的质量为4xg,所含碳水化合物的质量为(500﹣50﹣4x﹣x)g,
根据题意得:4x+(500﹣50﹣4x﹣x)≤85%×500,
解得:x≥25,
∴500﹣50﹣4x﹣x=325.
答:早餐中所含碳水化合物质量的最大值为325g.
23.如图,在△ABC中,∠B=40°,∠C=70°,AD是△ABC的角平分线,点E在BD上,点F在CA的延长线上,EF∥AD,求∠F的度数.
【分析】在△ABC中,利用内角和定理可求出∠BAC的度数,由AD平分线∠BAC,利用角平分线的定义可求出∠CAD的度数,由EF∥AD,再利用“两直线平行,同位角相等”即可求出∠F的度数.
解:在△ABC中,∠B=40°,∠C=70°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣40°﹣70°=70°.
∵AD平分线∠BAC,
∴∠CAD=∠BAC=×70°=35°.
∵EF∥AD,
∴∠F=∠CAD=35°.
24.已知关于x、y的二元一次方程组.
(1)若m=1,求方程组的解;
(2)若方程组的解中,x的值为正数,y的值为负数,求m的范围.
【分析】(1)把m=1代入方程组求出解即可;
(2)把m看做已知数表示出方程组的解,由x为正数,y为负数,确定出m的范围即可.
解:(1)当m=1,方程组为,
①+②得:3x=12,
解得:x=4,
把x=4代入②得:y=3,
∴方程组的解为;
(2)①+②得:3x=3m+9,
解得:x=m+3,
把x=m+3代入②得:m+3+y=5+2m,
解得:y=m+2,
由题意得,
解得:﹣3<m<﹣2.
25.如图所示,在△ABC中,BO、CO是角平分线.
(1)∠ABC=50°,∠ACB=60°,求∠BOC的度数,并说明理由.
(2)题(1)中,如将“∠ABC=50°,∠ACB=60°”改为“∠A=70°”,求∠BOC的度数.
(3)若∠A=n°,求∠BOC的度数.
【分析】如图,由BO、CO是角平分线得∠ABC=2∠1,∠ACB=2∠2,再利用三角形内角和得到∠ABC+∠ACB+∠A=180°,则2∠1+2∠2+∠A=180°,接着再根据三角形内角和得到∠1+∠2+∠BOC=180°,利用等式的性质进行变换可得∠BOC=90°+∠A,然后根据此结论分别解决(1)、(2)、(3).
解:如图,∵BO、CO是角平分线,
∴∠ABC=2∠1,∠ACB=2∠2,
∵∠ABC+∠ACB+∠A=180°,
∴2∠1+2∠2+∠A=180°,
∵∠1+∠2+∠BOC=180°,
∴2∠1+2∠2+2∠BOC=360°,
∴2∠BOC﹣∠A=180°,
∴∠BOC=90°+∠A,
(1)∵∠ABC=50°,∠ACB=60°,
∴∠A=180°﹣50°﹣60°=70°,
∴∠BOC=90°+×70°=125°;
(2)∠BOC=90°+∠A=125°;
(3)∠BOC=90°+n°.
26.有甲、乙两个长方形纸片,边长如图所示(m>0),面积分别为S甲和S乙.
(1)①计算:S甲= m2+12m+27 ,S乙= m2+10m+24 ;
②用“<”,“=”或“>”填空:S甲 > S乙.
(2)若一个正方形纸片的周长与乙长方形的周长相等,面积为S正.
①该正方形的边长是
m+5 (用含m的代数式表示);
②小方同学发现:S正与S乙的差与m无关.请判断小方的发现是否正确,并通过计算说明你的理由.
【分析】(1)①根据长方形的面积公式以及多项式乘多项式的乘法法则解决此题.
②通过作差法比较大小.
(2)①根据一个正方形纸片的周长与乙长方形的周长相等,求出正方形的边长.
②先用含有m的代数式表示出S正与S乙的差,进而判断S正与S乙的差与m的关系.
解:(1)①S甲=(m+9)(m+3)=m2+12m+27,S乙=(m+6)(m+4)=m2+10m+24.
故答案为:m2+12m+27,m2+10m+24.
②∵S甲﹣S乙
=m2+12m+27﹣(m2+10m+24)
=2m+3>0,
∴S甲>S乙.
故答案为:>.
(2)①∵C乙=2(m+6+m+4)=4m+20,
∴C正=4m+20.
∴该正方形的边长为.
故答案为:m+5.
②正确,理由如下:
∵=m2+10m+25,S乙=(m+6)(m+4)=m2+10m+24,
∴S正﹣S乙=(m2+10m+25)﹣(m2+10m+24)=1.
∴S正与S乙的差是1,故与m无关.
一、选择题(共42分。1-10每小题3分,11-16每小题3分).
1.计算:20( )
A.2
B.﹣2
C.1
D.﹣1
2.已知二元一次方程3x+2y=11,则( )
A.任何一对有理数都是它的解
B.只有一个解
C.只有两个解
D.有无数个解
3.如图,能判定EB∥AC的条件是( )
A.∠C=∠ABE
B.∠A=∠EBD
C.∠C=∠DBE
D.∠A=∠ABC
4.下列运算正确的是( )
A.x2+x=x3
B.2﹣1=﹣2
C.(x3)2÷x2=x4
D.(﹣m2)2=﹣m4
5.已知,a,b两个实数在数轴上的对应点如图所示,则下列各式一定成立的是( )
A.a﹣1>b﹣1
B.3a>3b
C.﹣a>﹣b
D.a+b>a﹣b
6.如果多项式x2+mx+16是一个完全平方式,则m的值是( )
A.±4
B.4
C.8
D.±8
7.下列从左到右的变形,是因式分解的是( )
A.(3﹣x)(3+x)=9﹣x2
B.(y+1)(y﹣3)=(3﹣y)(y+1)
C.4yz﹣2y2z+z=2y(2z﹣zy)+z
D.﹣8x2+8x﹣2=﹣2(2x﹣1)2
8.若关于x的不等式组恰有3个整数解,则字母a的取值范围是( )
A.a≤﹣1
B.﹣2≤a<﹣1
C.a<﹣1
D.﹣2<a≤﹣1
9.用加减法解方程组下列解法不正确的是( )
A.①×2﹣②×(﹣3),消去y
B.①×2﹣②×3,消去y
C.①×(﹣3)+②×2,消去x
D.①×3﹣②×2,消去x
10.下列长度的三条线段,能组成三角形的是( )
A.1,2,4
B.2,2,4
C.2,3,6
D.3,4,5
11.在如图所示的网格中,有两个完全相同的直角三角形纸片,如果把其中一个三角形纸片先横向平移m格,再纵向平移n格,就能使它的一条边与另一个三角形纸片的一条边重合,拼接成一个四边形,那么m+n的结果( )
A.只有一个确定的值
B.有两个不同的值
C.有三个不同的值
D.有三个以上不同的值
12.下列命题是真命题的是( )
A.如果a2=b2,那么a=b
B.如果两个角是同位角,那么这两个角相等
C.相等的两个角是对顶角
D.平面内,垂直于同一条直线的两条直线平行
13.我国是一个严重缺水的国家,大家应倍加珍惜水资源,节约用水,据测试,拧不紧水龙头每秒会滴下2滴水,每滴水约0.05毫升,小明同学在洗手后,没有把水龙头拧紧,当小明离开4小时后,水龙头滴了( )毫升水.(用科学记数法表示)
A.1440
B.1.44×103
C.0.144×104
D.144×102
14.甲乙两人在相距18千米的两地,若同时出发相向而行,经2小时相遇;若同向而行,且甲比乙先出发1小时追击乙,那么在乙出发后经4小时两人相遇,求甲、乙两人的速度.设甲的速度为x千米/小时,乙的速度为y千米/小时,则可列方程组为( )
A.
B.
C.
D.
15.利用尺规作图,作△ABC边上的高AD,正确的是( )
A.
B.
C.
D.
16.我们所学的多项式因分解的方法主要有:①提公因式法;②平方差公式法;③完全平方公式法.现将多项式(x﹣y)3+4(y﹣x)进行因式分解,使用的方法有( )
A.①②
B.①③
C.②③
D.①②③
二、填空题(本大题有3个小题,共9分。每小题3分,把答案写在题中横线上)
17.一元一次不等式5x+10≥0的负整数解是
.
18.已知三角形的一个内角α是另一个内角β的两倍,当α=80°时,这个三角形的最小内角是
.
19.若a+b=2,ab=﹣3,则代数式a3b+2a2b2+ab3的值为
.
三、解答题(本大题有7个小题,共69分,解答应写出必要的文字说明、证明过程或演算步骤)。
20.已知是方程2x﹣ay=9的一个解,解决下列问题:
(1)求a的值;
(2)化简并求值:(a﹣1)(a+1)﹣2(a﹣1)2+a(a﹣3).
21.如图,DE⊥BC,AF⊥BC,∠1+∠2=180°.
求证:∠FGA+∠CAB=180°
22.某校学生社会实践小组开展调查,获取了本校食堂学生早餐的营养情况,如图是调查报告中的一部分,根据所得信息,解答下列问题.
调查报告1.早餐总质量为500g;2.早餐的成分是蛋白质、脂肪、矿物质和碳水化合物;3.所含蛋白质的质量与矿物质之比为4:1;4.脂肪占早餐总质量的10%.
(1)早餐中所含脂肪的质量是
g.
(2)若早餐中蛋白质和碳水化合物所占百分比的和不高于85%,求早餐中所含碳水化合物质量的最大值.
23.如图,在△ABC中,∠B=40°,∠C=70°,AD是△ABC的角平分线,点E在BD上,点F在CA的延长线上,EF∥AD,求∠F的度数.
24.已知关于x、y的二元一次方程组.
(1)若m=1,求方程组的解;
(2)若方程组的解中,x的值为正数,y的值为负数,求m的范围.
25.如图所示,在△ABC中,BO、CO是角平分线.
(1)∠ABC=50°,∠ACB=60°,求∠BOC的度数,并说明理由.
(2)题(1)中,如将“∠ABC=50°,∠ACB=60°”改为“∠A=70°”,求∠BOC的度数.
(3)若∠A=n°,求∠BOC的度数.
26.有甲、乙两个长方形纸片,边长如图所示(m>0),面积分别为S甲和S乙.
(1)①计算:S甲=
,S乙=
;
②用“<”,“=”或“>”填空:S甲
S乙.
(2)若一个正方形纸片的周长与乙长方形的周长相等,面积为S正.
①该正方形的边长是
(用含m的代数式表示);
②小方同学发现:S正与S乙的差与m无关.请判断小方的发现是否正确,并通过计算说明你的理由.
参考答案
一、选择题(本大题有16个小题,共42分。1-10每小题3分,11-16每小题3分。在每小题给出的四个选项中,只有一项符合题目要求)。
1.计算:20( )
A.2
B.﹣2
C.1
D.﹣1
【分析】根据零指数幂的意义即可求出答案.
解:原式=1,
故选:C.
2.已知二元一次方程3x+2y=11,则( )
A.任何一对有理数都是它的解
B.只有一个解
C.只有两个解
D.有无数个解
【分析】将二元一次方程3x+2y=11,化为用一个未知数表示另一个未知数的情况,即可解答.
解:原方程可化为y=,可见对于每一个x的值,y都有唯一的值和它相对应,故方程有无数个解.
故选:D.
3.如图,能判定EB∥AC的条件是( )
A.∠C=∠ABE
B.∠A=∠EBD
C.∠C=∠DBE
D.∠A=∠ABC
【分析】通过角相等判定两直线平行,则判断两角是否能推出同位角或内错角相等即可.
解:∵只有同位角相等,内错角相等,同旁内角互补才能判断两直线平行,
只有选项C中∠C=∠DBE是同位角相等,故能判定两直线平行,
故选:C.
4.下列运算正确的是( )
A.x2+x=x3
B.2﹣1=﹣2
C.(x3)2÷x2=x4
D.(﹣m2)2=﹣m4
【分析】根据合并同类项法则,负整数指数幂,幂的乘方和积的乘方,同底数幂的除法分别求出每个式子的值,再进行判断即可.
解:A、x2和x不能合并,故本选项不符合题意;
B、2﹣1=,故本选项不符合题意;
C、(x3)2÷x2=x4,故本选项符合题意;
D、(﹣m2)2=m4,故本选项不符合题意;
故选:C.
5.已知,a,b两个实数在数轴上的对应点如图所示,则下列各式一定成立的是( )
A.a﹣1>b﹣1
B.3a>3b
C.﹣a>﹣b
D.a+b>a﹣b
【分析】首先根据图示,可得a<b<0,然后根据不等式的性质,逐一判断出哪个式子一定成立即可.
解:根据图示,可得a<b<0,
∵a<b,
∴a﹣1<b﹣1,
∴选项A不正确;
∵a<b,
∴3a<3b,
∴选项B不正确;
∵a<b,
∴﹣a>﹣b,
∴选项C正确;
∵a<b<0,
∴b<﹣b,
∴a+b<a﹣b,
∴选项D不正确.
故选:C.
6.如果多项式x2+mx+16是一个完全平方式,则m的值是( )
A.±4
B.4
C.8
D.±8
【分析】根据完全平方公式有两个,则x2+mx+16=(x±4)2,展开即可求解;
解:∵完全平方公式有两个,
∴x2+mx+16=(x±4)2,
∴m=±8;
故选:D.
7.下列从左到右的变形,是因式分解的是( )
A.(3﹣x)(3+x)=9﹣x2
B.(y+1)(y﹣3)=(3﹣y)(y+1)
C.4yz﹣2y2z+z=2y(2z﹣zy)+z
D.﹣8x2+8x﹣2=﹣2(2x﹣1)2
【分析】分别利用因式分解的定义分析得出答案.
解:A、(3﹣x)(3+x)=9﹣x2,是整式的乘法运算,故此选项错误;
B、(y+1)(y﹣3)≠(3﹣y)(y+1),不符合因式分解的定义,故此选项错误;
C、4yz﹣2y2z+z=2y(2z﹣zy)+z,不符合因式分解的定义,故此选项错误;
D、﹣8x2+8x﹣2=﹣2(2x﹣1)2,正确.
故选:D.
8.若关于x的不等式组恰有3个整数解,则字母a的取值范围是( )
A.a≤﹣1
B.﹣2≤a<﹣1
C.a<﹣1
D.﹣2<a≤﹣1
【分析】先确定不等式组的整数解,再求出a的范围即可.
解:∵关于x的不等式组恰有3个整数解,
∴整数解为1,0,﹣1,
∴﹣2≤a<﹣1,
故选:B.
9.用加减法解方程组下列解法不正确的是( )
A.①×2﹣②×(﹣3),消去y
B.①×2﹣②×3,消去y
C.①×(﹣3)+②×2,消去x
D.①×3﹣②×2,消去x
【分析】方程组利用加减消元法变形,即可做出判断.
解:用加减法解方程组,可以①×2﹣②×3,消去y;①×(﹣3)+②×2,消去x;①×3﹣②×2,消去x,
故选:A.
10.下列长度的三条线段,能组成三角形的是( )
A.1,2,4
B.2,2,4
C.2,3,6
D.3,4,5
【分析】根据三角形的三边满足两边之和大于第三边来进行判断.
解:A、1+2<4,不能构成三角形,不符合题意;
B、2+2=4,不能构成三角形,不符合题意;
C、2+3<6,不能构成三角形,不符合题意;
D、3+4>5,能构成三角形,符合题意.
故选:D.
11.在如图所示的网格中,有两个完全相同的直角三角形纸片,如果把其中一个三角形纸片先横向平移m格,再纵向平移n格,就能使它的一条边与另一个三角形纸片的一条边重合,拼接成一个四边形,那么m+n的结果( )
A.只有一个确定的值
B.有两个不同的值
C.有三个不同的值
D.有三个以上不同的值
【分析】根据两个全等的直角三角形可以组成一个矩形或一个平行四边形可得出答案.
解:(1)当两斜边重合的时候可组成一个矩形,此时m=2,n=3,m+n=5;
(2)当两直角边重合时有两种情况,①短边重合,此时m=2,n=3,m+n=5;
②长边重合,此时m=2,n=5,m+n=7.
综上可得:m+n=5或7.
故选:B.
12.下列命题是真命题的是( )
A.如果a2=b2,那么a=b
B.如果两个角是同位角,那么这两个角相等
C.相等的两个角是对顶角
D.平面内,垂直于同一条直线的两条直线平行
【分析】利用平方的定义、平行线的性质、对顶角的性质及平面内两直线的位置关系分别判断后即可确定正确的选项.
解:A、如果a2=b2,那么a=±b,故错误,是假命题;
B、两直线平行,同位角才相等,故错误,是假命题;
C、相等的两个角不一定是对顶角,故错误,是假命题;
D、平面内,垂直于同一条直线的两条直线平行,正确,是真命题,
故选:D.
13.我国是一个严重缺水的国家,大家应倍加珍惜水资源,节约用水,据测试,拧不紧水龙头每秒会滴下2滴水,每滴水约0.05毫升,小明同学在洗手后,没有把水龙头拧紧,当小明离开4小时后,水龙头滴了( )毫升水.(用科学记数法表示)
A.1440
B.1.44×103
C.0.144×104
D.144×102
【分析】首先求出4小时滴的水量,再利用科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.
解:∵拧不紧水龙头每秒会滴下2滴水,每滴水约0.05毫升,小明同学在洗手后,没有把水龙头拧紧,
∴当小明离开4小时后,水龙头滴了2×0.05×4×60×60=1440(毫升),
将1440用科学记数法表示为:1.44×103.
故选:B.
14.甲乙两人在相距18千米的两地,若同时出发相向而行,经2小时相遇;若同向而行,且甲比乙先出发1小时追击乙,那么在乙出发后经4小时两人相遇,求甲、乙两人的速度.设甲的速度为x千米/小时,乙的速度为y千米/小时,则可列方程组为( )
A.
B.
C.
D.
【分析】根据题意可得等量关系:①甲2小时的路程+乙2小时的路程=18千米;②甲5小时的路程﹣乙4小时的路程=18千米,根据等量关系列出方程组即可.
解:设甲的速度为x千米/小时,乙的速度为y千米/小时,
由题意得:,
故选:B.
15.利用尺规作图,作△ABC边上的高AD,正确的是( )
A.
B.
C.
D.
【分析】过点A作BC的垂线,垂足为D,则AD即为所求.
解:过点A作BC的垂线,垂足为D,
故选:B.
16.我们所学的多项式因分解的方法主要有:①提公因式法;②平方差公式法;③完全平方公式法.现将多项式(x﹣y)3+4(y﹣x)进行因式分解,使用的方法有( )
A.①②
B.①③
C.②③
D.①②③
【分析】直接利用提取公因式法以及公式法分解因式得出答案.
解:(x﹣y)3+4(y﹣x)
=(x﹣y)3﹣4(x﹣y)
=(x﹣y)[(x﹣y)2﹣4]
=(x﹣y)(x﹣y+2)(x﹣y﹣2),
故将多项式(x﹣y)3+4(y﹣x)进行因式分解,使用的方法有:①提公因式法;②平方差公式法;
故选:A.
二、填空题(本大题有3个小题,共9分。每小题3分,把答案写在题中横线上)
17.一元一次不等式5x+10≥0的负整数解是
﹣1,﹣2 .
【分析】首先利用不等式的基本性质解不等式,再从不等式的解集中找出适合条件的负整数即可.
解:5x+10≥0,
∴5x≥﹣10,
∴x≥﹣2,
则不等式的负整数解为﹣1,﹣2,
故答案为﹣1,﹣2.
18.已知三角形的一个内角α是另一个内角β的两倍,当α=80°时,这个三角形的最小内角是
40° .
【分析】根据题意可以得到α=2β,当当α=80°时,求出β,再根据三角形内角和定理,求出最后一个角,进行大小比较,即可得到答案.
解:∵三角形的一个内角α是另一个内角β的两倍,
∴α=2β,
当α=80°时,
则β=40°,
∴三角形的最后一个内角为:180°﹣80°﹣40°=60°,
∵40°<60°<80°,
∴这个三角形的最小内角是40°,
故答案为:40°.
19.若a+b=2,ab=﹣3,则代数式a3b+2a2b2+ab3的值为 ﹣12 .
【分析】根据a3b+2a2b2+ab3=ab(a2+2ab+b2)=ab(a+b)2,结合已知数据即可求出代数式a3b+2a2b2+ab3的值.
解:∵a+b=2,ab=﹣3,
∴a3b+2a2b2+ab3=ab(a2+2ab+b2),
=ab(a+b)2,
=﹣3×4,
=﹣12.
故答案为:﹣12.
三、解答题(本大题有7个小题,共69分,解答应写出必要的文字说明、证明过程或演算步骤)。
20.已知是方程2x﹣ay=9的一个解,解决下列问题:
(1)求a的值;
(2)化简并求值:(a﹣1)(a+1)﹣2(a﹣1)2+a(a﹣3).
【分析】(1)把x、y的值代入方程可求得a的值;
(2)根据乘法公式先化简,再把a的值代入求值即可.
解:(1)∵是方程2x﹣ay=9的一个解,
∴6﹣a=9,解得a=﹣3;
(2)(a﹣1)(a+1)﹣2(a﹣1)2+a(a﹣3)
=a2﹣1﹣2(a2﹣2a+1)+a2﹣3a
=a2﹣1﹣2a2+4a﹣2+a2﹣3a
=a﹣3,
把a=﹣3代入上式可得:原式=﹣3﹣3=﹣6.
21.如图,DE⊥BC,AF⊥BC,∠1+∠2=180°.
求证:∠FGA+∠CAB=180°
【分析】证明AF∥DE,由平行线的性质得出∠2+∠3=180°,证出∠1=∠3,得出GF∥AC,由平行线的性质即可得出结论.
【解答】证明:∵DE⊥BC,AF⊥BC,
∴AF∥DE,
∴∠2+∠3=180°,
∵∠1+∠2=180°,
∴∠1=∠3,
∴GF∥AC,
∴∠FGA+∠CAB=180°.
22.某校学生社会实践小组开展调查,获取了本校食堂学生早餐的营养情况,如图是调查报告中的一部分,根据所得信息,解答下列问题.
调查报告1.早餐总质量为500g;2.早餐的成分是蛋白质、脂肪、矿物质和碳水化合物;3.所含蛋白质的质量与矿物质之比为4:1;4.脂肪占早餐总质量的10%.
(1)早餐中所含脂肪的质量是
50 g.
(2)若早餐中蛋白质和碳水化合物所占百分比的和不高于85%,求早餐中所含碳水化合物质量的最大值.
【分析】(1)根据脂肪所占的百分比结合这份快餐的总质量,即可求出结论;
(2)设所含矿物质的质量为xg,则所含蛋白质的质量为4xg,所含碳水化合物的质量为(500﹣50﹣4x﹣x)g,由这份快餐中蛋白质和碳水化合物所占百分比的和不高于85%,即可得出关于x的一元一次不等式,解之取其其中的最小值即可得出结论.
解:(1)500×10%=50(g).
∴这份快餐中所含脂肪质量为50g.
故答案为50;
(2)设所含矿物质的质量为xg,则所含蛋白质的质量为4xg,所含碳水化合物的质量为(500﹣50﹣4x﹣x)g,
根据题意得:4x+(500﹣50﹣4x﹣x)≤85%×500,
解得:x≥25,
∴500﹣50﹣4x﹣x=325.
答:早餐中所含碳水化合物质量的最大值为325g.
23.如图,在△ABC中,∠B=40°,∠C=70°,AD是△ABC的角平分线,点E在BD上,点F在CA的延长线上,EF∥AD,求∠F的度数.
【分析】在△ABC中,利用内角和定理可求出∠BAC的度数,由AD平分线∠BAC,利用角平分线的定义可求出∠CAD的度数,由EF∥AD,再利用“两直线平行,同位角相等”即可求出∠F的度数.
解:在△ABC中,∠B=40°,∠C=70°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣40°﹣70°=70°.
∵AD平分线∠BAC,
∴∠CAD=∠BAC=×70°=35°.
∵EF∥AD,
∴∠F=∠CAD=35°.
24.已知关于x、y的二元一次方程组.
(1)若m=1,求方程组的解;
(2)若方程组的解中,x的值为正数,y的值为负数,求m的范围.
【分析】(1)把m=1代入方程组求出解即可;
(2)把m看做已知数表示出方程组的解,由x为正数,y为负数,确定出m的范围即可.
解:(1)当m=1,方程组为,
①+②得:3x=12,
解得:x=4,
把x=4代入②得:y=3,
∴方程组的解为;
(2)①+②得:3x=3m+9,
解得:x=m+3,
把x=m+3代入②得:m+3+y=5+2m,
解得:y=m+2,
由题意得,
解得:﹣3<m<﹣2.
25.如图所示,在△ABC中,BO、CO是角平分线.
(1)∠ABC=50°,∠ACB=60°,求∠BOC的度数,并说明理由.
(2)题(1)中,如将“∠ABC=50°,∠ACB=60°”改为“∠A=70°”,求∠BOC的度数.
(3)若∠A=n°,求∠BOC的度数.
【分析】如图,由BO、CO是角平分线得∠ABC=2∠1,∠ACB=2∠2,再利用三角形内角和得到∠ABC+∠ACB+∠A=180°,则2∠1+2∠2+∠A=180°,接着再根据三角形内角和得到∠1+∠2+∠BOC=180°,利用等式的性质进行变换可得∠BOC=90°+∠A,然后根据此结论分别解决(1)、(2)、(3).
解:如图,∵BO、CO是角平分线,
∴∠ABC=2∠1,∠ACB=2∠2,
∵∠ABC+∠ACB+∠A=180°,
∴2∠1+2∠2+∠A=180°,
∵∠1+∠2+∠BOC=180°,
∴2∠1+2∠2+2∠BOC=360°,
∴2∠BOC﹣∠A=180°,
∴∠BOC=90°+∠A,
(1)∵∠ABC=50°,∠ACB=60°,
∴∠A=180°﹣50°﹣60°=70°,
∴∠BOC=90°+×70°=125°;
(2)∠BOC=90°+∠A=125°;
(3)∠BOC=90°+n°.
26.有甲、乙两个长方形纸片,边长如图所示(m>0),面积分别为S甲和S乙.
(1)①计算:S甲= m2+12m+27 ,S乙= m2+10m+24 ;
②用“<”,“=”或“>”填空:S甲 > S乙.
(2)若一个正方形纸片的周长与乙长方形的周长相等,面积为S正.
①该正方形的边长是
m+5 (用含m的代数式表示);
②小方同学发现:S正与S乙的差与m无关.请判断小方的发现是否正确,并通过计算说明你的理由.
【分析】(1)①根据长方形的面积公式以及多项式乘多项式的乘法法则解决此题.
②通过作差法比较大小.
(2)①根据一个正方形纸片的周长与乙长方形的周长相等,求出正方形的边长.
②先用含有m的代数式表示出S正与S乙的差,进而判断S正与S乙的差与m的关系.
解:(1)①S甲=(m+9)(m+3)=m2+12m+27,S乙=(m+6)(m+4)=m2+10m+24.
故答案为:m2+12m+27,m2+10m+24.
②∵S甲﹣S乙
=m2+12m+27﹣(m2+10m+24)
=2m+3>0,
∴S甲>S乙.
故答案为:>.
(2)①∵C乙=2(m+6+m+4)=4m+20,
∴C正=4m+20.
∴该正方形的边长为.
故答案为:m+5.
②正确,理由如下:
∵=m2+10m+25,S乙=(m+6)(m+4)=m2+10m+24,
∴S正﹣S乙=(m2+10m+25)﹣(m2+10m+24)=1.
∴S正与S乙的差是1,故与m无关.
同课章节目录
