山东省菏泽市单县2020-2021学年九年级下学期期中数学试题(word版无答案)
文档属性
| 名称 | 山东省菏泽市单县2020-2021学年九年级下学期期中数学试题(word版无答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 821.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-18 00:00:00 | ||
图片预览


文档简介
2020—2021学年度第二学期期中质量检测九年级数学试题
一、选择题(本大题共8个小题,每小题3分,共24分,在每小题给出的四个选项A、B、C、D中,只有一个选项是正确的,请把正确的选项填在答题卡相应位置.)
1.
下列计算正确的是( )
A.
B.
C.
D.
2.
下列运算正确的是( )
A.
B.
C.
D.
3.
将一副三角板()按如图所示方式摆放,使得,则等于( )
A.
B.
C.
D.
4.
如图,一个几何体由5个大小相同、棱长为1的小正方体搭成,下列说法正确的是( ).
A.
主视图的面积为4
B.
左视图的面积为4
C.
俯视图的面积为3
D.
三种视图的面积都是4
5.
如图,折叠矩形的一边,使点落在边的点处,已知,.则的值是(
)
A.
B.
C.
2
D.
5
6.
如图,将沿边上的中线平移到的位置,已知的面积为9,阴影部分三角形的面积为4.若,则等于(
)
A.
2
B.
3
C.
4
D.
5
7.
《孙子算经》中有一道题,原文是:“今有木,不知长短.引绳度之,余绳四足五寸;屈绳量之,不足一尺.木长几何?”意思是:用一根绳子去量一根长木,绳子还剩余尺.将绳子对折再量长木,长木还剩余尺,问木长多少尺,现设绳长尺,木长尺,则可列二元一次方程组为( )
A.
B.
C.
D.
8.
如图,函数和(是常数,且)在同一平面直角坐标系的图象可能是(
)
A.
B.
C.
D.
二、填空题(本大题共有6个小题,每小题3分,共18分,只要求把结果填写在答题卡的相应区域内)
9
因式分解:_____.
10.
若一组数据的平均数为6,众数为5,则这组数据的方差为__________.
11.
已知关于x的一元二次方程有一个根为,则a的值为________.
12.
如图,O为Rt△ABC直角边AC上一点,以OC为半径⊙O与斜边AB相切于点D,交OA于点E,已知BC=,AC=3.则图中阴影部分的面积是_____.
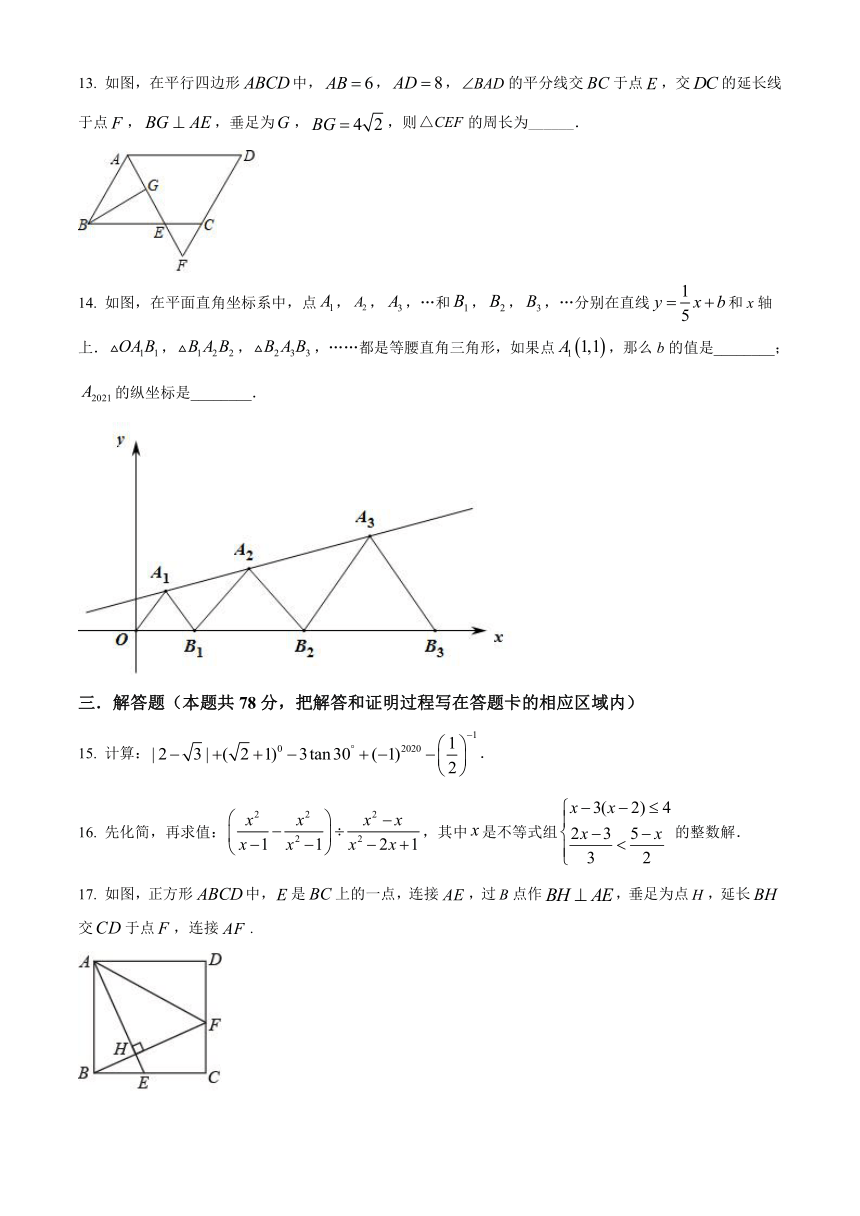
13.
如图,在平行四边形中,,,的平分线交于点,交的延长线于点,,垂足为,,则的周长为______.
14.
如图,在平面直角坐标系中,点,,,…和,,,…分别在直线和x轴上.,,,……都是等腰直角三角形,如果点,那么b的值是________;的纵坐标是________.
三.解答题(本题共78分,把解答和证明过程写在答题卡的相应区域内)
15.
计算:.
16.
先化简,再求值:,其中是不等式组的整数解.
17.
如图,正方形中,是上的一点,连接,过点作,垂足为点,延长交于点,连接.
(1)求证:.
(2)若正方形边长是5,,求的长.
18.
如图,两座建筑物的水平距离为.从点测得点的仰角为53°
,从点测得点的俯角为37°
,求两座建筑物的高度(参考数据:
19.
已知一次函数的图象与反比例函数的图象交于点,与轴交于点,若,且.
(1)求反比例函数与一次函数的表达式;
(2)若点为x轴上一点,是等腰三角形,求点的坐标.
20.
端午节是我国的传统节日,人们素有吃粽子的习俗,某商场在端午节来临之际用3000元购进、两种粽子1100个,购买种粽子与购买种粽子的费用相同,已知粽子的单价是种粽子单价的1.2倍.
(1)求、两种粽子的单价各是多少?
(2)若计划用不超过7000元的资金再次购买、两种粽子共2600个,已知、两种粽子的进价不变,求中粽子最多能购进多少个?
21.
某体育老师统计了七年级甲、乙两个班女生身高,并绘制了以下不完整的统计图.
请根据图中信息,解决下列问题:
(1)两个班共有女生多少人?
(2)将频数分布直方图补充完整;
(3)求扇形统计图中部分所对应的扇形圆心角度数;
(4)身高在的5人中,甲班有3人,乙班有2人,现从中随机抽取两人补充到学校国旗队.请用列表法或画树状图法,求这两人来自同一班级的概率.
22.
如图,是直径,是上一点,是的中点,为延长线上一点,且,与交于点,与交于点.
(1)求证:是的切线;
(2)若,,求直径的长.
23.
如图1,在Rt中,∠B=90°,AB=4,BC=2,点D,E分别是边BC,AC的中点,连接DE.将绕点C逆时针方向旋转,记旋转角为α.
(1)问题发现
①当α=0°时,=
;
②当α=180°时,=
;
(2)拓展探究
试判断当0°<α<360°时,的大小有无变化?请仅就图2的情形给出证明;
(3)问题解决
当绕点C逆时针旋转至A,B,E三点在同一条直线上时,求线段BD的长.
24.
已知抛物线的对称轴是直线,与轴相交于,两点(点在点右侧),与轴交于点.
(1)求抛物线的解析式和,两点的坐标;
(2)如图1,若点是抛物线上、两点之间的一个动点(不与、重合),是否存在点,使四边形的面积最大?若存在,求点的坐标及四边形面积的最大值;若不存在,请说明理由;
(3)如图2,若点是抛物线上任意一点,过点作轴的平行线,交直线于点,当时,求点的坐标.
一、选择题(本大题共8个小题,每小题3分,共24分,在每小题给出的四个选项A、B、C、D中,只有一个选项是正确的,请把正确的选项填在答题卡相应位置.)
1.
下列计算正确的是( )
A.
B.
C.
D.
2.
下列运算正确的是( )
A.
B.
C.
D.
3.
将一副三角板()按如图所示方式摆放,使得,则等于( )
A.
B.
C.
D.
4.
如图,一个几何体由5个大小相同、棱长为1的小正方体搭成,下列说法正确的是( ).
A.
主视图的面积为4
B.
左视图的面积为4
C.
俯视图的面积为3
D.
三种视图的面积都是4
5.
如图,折叠矩形的一边,使点落在边的点处,已知,.则的值是(
)
A.
B.
C.
2
D.
5
6.
如图,将沿边上的中线平移到的位置,已知的面积为9,阴影部分三角形的面积为4.若,则等于(
)
A.
2
B.
3
C.
4
D.
5
7.
《孙子算经》中有一道题,原文是:“今有木,不知长短.引绳度之,余绳四足五寸;屈绳量之,不足一尺.木长几何?”意思是:用一根绳子去量一根长木,绳子还剩余尺.将绳子对折再量长木,长木还剩余尺,问木长多少尺,现设绳长尺,木长尺,则可列二元一次方程组为( )
A.
B.
C.
D.
8.
如图,函数和(是常数,且)在同一平面直角坐标系的图象可能是(
)
A.
B.
C.
D.
二、填空题(本大题共有6个小题,每小题3分,共18分,只要求把结果填写在答题卡的相应区域内)
9
因式分解:_____.
10.
若一组数据的平均数为6,众数为5,则这组数据的方差为__________.
11.
已知关于x的一元二次方程有一个根为,则a的值为________.
12.
如图,O为Rt△ABC直角边AC上一点,以OC为半径⊙O与斜边AB相切于点D,交OA于点E,已知BC=,AC=3.则图中阴影部分的面积是_____.
13.
如图,在平行四边形中,,,的平分线交于点,交的延长线于点,,垂足为,,则的周长为______.
14.
如图,在平面直角坐标系中,点,,,…和,,,…分别在直线和x轴上.,,,……都是等腰直角三角形,如果点,那么b的值是________;的纵坐标是________.
三.解答题(本题共78分,把解答和证明过程写在答题卡的相应区域内)
15.
计算:.
16.
先化简,再求值:,其中是不等式组的整数解.
17.
如图,正方形中,是上的一点,连接,过点作,垂足为点,延长交于点,连接.
(1)求证:.
(2)若正方形边长是5,,求的长.
18.
如图,两座建筑物的水平距离为.从点测得点的仰角为53°
,从点测得点的俯角为37°
,求两座建筑物的高度(参考数据:
19.
已知一次函数的图象与反比例函数的图象交于点,与轴交于点,若,且.
(1)求反比例函数与一次函数的表达式;
(2)若点为x轴上一点,是等腰三角形,求点的坐标.
20.
端午节是我国的传统节日,人们素有吃粽子的习俗,某商场在端午节来临之际用3000元购进、两种粽子1100个,购买种粽子与购买种粽子的费用相同,已知粽子的单价是种粽子单价的1.2倍.
(1)求、两种粽子的单价各是多少?
(2)若计划用不超过7000元的资金再次购买、两种粽子共2600个,已知、两种粽子的进价不变,求中粽子最多能购进多少个?
21.
某体育老师统计了七年级甲、乙两个班女生身高,并绘制了以下不完整的统计图.
请根据图中信息,解决下列问题:
(1)两个班共有女生多少人?
(2)将频数分布直方图补充完整;
(3)求扇形统计图中部分所对应的扇形圆心角度数;
(4)身高在的5人中,甲班有3人,乙班有2人,现从中随机抽取两人补充到学校国旗队.请用列表法或画树状图法,求这两人来自同一班级的概率.
22.
如图,是直径,是上一点,是的中点,为延长线上一点,且,与交于点,与交于点.
(1)求证:是的切线;
(2)若,,求直径的长.
23.
如图1,在Rt中,∠B=90°,AB=4,BC=2,点D,E分别是边BC,AC的中点,连接DE.将绕点C逆时针方向旋转,记旋转角为α.
(1)问题发现
①当α=0°时,=
;
②当α=180°时,=
;
(2)拓展探究
试判断当0°<α<360°时,的大小有无变化?请仅就图2的情形给出证明;
(3)问题解决
当绕点C逆时针旋转至A,B,E三点在同一条直线上时,求线段BD的长.
24.
已知抛物线的对称轴是直线,与轴相交于,两点(点在点右侧),与轴交于点.
(1)求抛物线的解析式和,两点的坐标;
(2)如图1,若点是抛物线上、两点之间的一个动点(不与、重合),是否存在点,使四边形的面积最大?若存在,求点的坐标及四边形面积的最大值;若不存在,请说明理由;
(3)如图2,若点是抛物线上任意一点,过点作轴的平行线,交直线于点,当时,求点的坐标.
同课章节目录
