3.6 整式的加减课件(共19张PPT)
文档属性
| 名称 | 3.6 整式的加减课件(共19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 955.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-18 00:00:00 | ||
图片预览



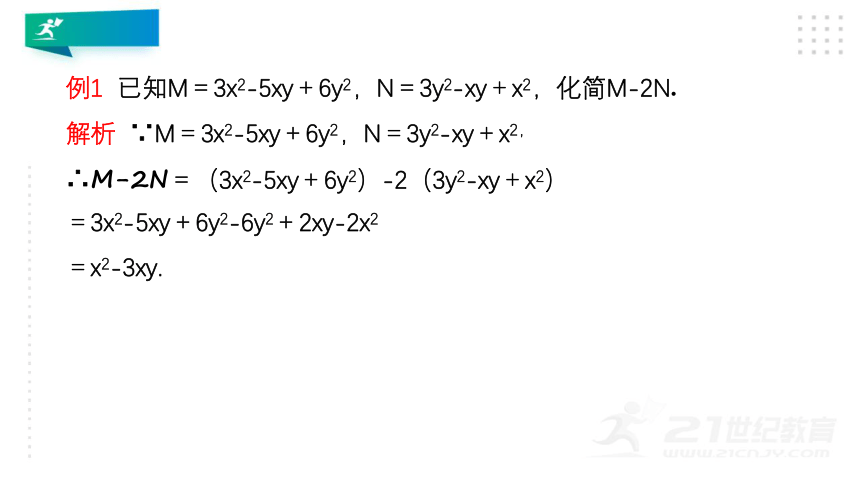


文档简介
(共19张PPT)
第三章
整式及其加减
6
整式的加减
知识点一
整式的加减
运算法则:
进行整式加减运算时,如果遇到括号要先去括号,再合并同类项.
知识点一
整式的加减
重要提示:(1)整式加减的一般步骤:①如果有括号,先去括号;②如果有同类项,要合并同类项;③如果运算结果是多项式,把这个多项式按某一字母的降(升)幂排列.
(2)整式的加减运算结果要求最简,即最后结果中:①不能再有同类项;②含字母项的系数不能出现带分数,是带分数的要化成假分数;③一般按照某一字母的升幂或降幂排列;④一般情况下结果不含括号.
(3)整式加减的一般步骤并不绝对,在具体运算中,也可以先将同类项合并,再去括号,但要按运算顺序进行.
(4)整式加减的基础是合并同类项法则和去括号法则;整式加减的实质是去括号与合并同类项;整式加减的目的是化简整式.
例1
已知M=3x2-5xy+6y2,N=3y2-xy+x2,化简M-2N.
例1
已知M=3x2-5xy+6y2,N=3y2-xy+x2,化简M-2N.
解析
∵M=3x2-5xy+6y2,N=3y2-xy+x2,
∴M-2N=(3x2-5xy+6y2)-2(3y2-xy+x2)
=3x2-5xy+6y2-6y2+2xy-2x2
=x2-3xy.
例1
已知M=3x2-5xy+6y2,N=3y2-xy+x2,化简M-2N.
解析
∵M=3x2-5xy+6y2,N=3y2-xy+x2,
∴M-2N=(3x2-5xy+6y2)-2(3y2-xy+x2)
=3x2-5xy+6y2-6y2+2xy-2x2
=x2-3xy.
特别提示
将M和N看成一个整体代入,代入时,为防止出现符号错误,注意添加括号.
知识点二
整式的化简求值
整式化简求值的步骤:
一化:化简
二代:代入求值
三计算:进行计算
经典例题
题型一
多项式的值与某个字母无关的问题
例1
已知(2x2+ax-y+b)-(2bx2-3x+5y-1)的值与字母x的取值无关,求3(a2-ab-b2)-(4a2+ab+b2)的值.
解析
(2x2+ax-y+b)-(2bx2-3x+5y-1)
=2x2+ax-y+b-2bx2+3x-5y+1
=(2-2b)x2+(a+3)x+(-y-5y+b+1).
由题意可知2-2b=0,a+3=0,所以b=1,a=-3.
3(a2-ab-b2)-(4a2+ab+b2)
=3a2-3ab-3b2-4a2-ab-b2
=-a2-4ab-4b2.
当b=1,a=-3时,
原式=-(-3)2-4x(-3)x1-4x12=-1.
点拨
整式经过化简后,若含某个字母的项的系数都等于0,则这个整式的值与该字母的取值无关;反之当某个整式的值与某个字母的取值无关时,则整式中含该字母的项的系数都等于0.
题型二
整式加减的实际应用
例2
已知一个三角形的第一条边长为(a+3b)厘米,第二条边比第一条边短(b-1)厘米,第三条边比第二条边长3厘米.
(1)请用式子表示该三角形的周长;
(2)当a=2b=3时,求此三角形的周长.
解析
(1)根据题意,得第二条边长为(a+3b)-(b-1)=(a+2b+1)厘米,第三条边长为a+2b+1+3=(a+2b+4)厘米,所以该三角形的周长为(a+3b)+(a+2b+1)+(a+2b+4)=(3a+7b+5)厘米.
(2)当a=2,b=3时,此三角形的周长为3a+7b+5=6+21+5=32(厘米).
解析
(1)根据题意,得第二条边长为(a+3b)-(b-1)=(a+2b+1)厘米,第三条边长为a+2b+1+3=(a+2b+4)厘米,所以该三角形的周长为(a+3b)+(a+2b+1)+(a+2b+4)=(3a+7b+5)厘米.
(2)当a=2,b=3时,此三角形的周长为3a+7b+5=6+21+5=32(厘米).
特别提示
正确求出第二条边和第三条边的长是解此题的关键.
第三章
整式及其加减
6
整式的加减
知识点一
整式的加减
运算法则:
进行整式加减运算时,如果遇到括号要先去括号,再合并同类项.
知识点一
整式的加减
重要提示:(1)整式加减的一般步骤:①如果有括号,先去括号;②如果有同类项,要合并同类项;③如果运算结果是多项式,把这个多项式按某一字母的降(升)幂排列.
(2)整式的加减运算结果要求最简,即最后结果中:①不能再有同类项;②含字母项的系数不能出现带分数,是带分数的要化成假分数;③一般按照某一字母的升幂或降幂排列;④一般情况下结果不含括号.
(3)整式加减的一般步骤并不绝对,在具体运算中,也可以先将同类项合并,再去括号,但要按运算顺序进行.
(4)整式加减的基础是合并同类项法则和去括号法则;整式加减的实质是去括号与合并同类项;整式加减的目的是化简整式.
例1
已知M=3x2-5xy+6y2,N=3y2-xy+x2,化简M-2N.
例1
已知M=3x2-5xy+6y2,N=3y2-xy+x2,化简M-2N.
解析
∵M=3x2-5xy+6y2,N=3y2-xy+x2,
∴M-2N=(3x2-5xy+6y2)-2(3y2-xy+x2)
=3x2-5xy+6y2-6y2+2xy-2x2
=x2-3xy.
例1
已知M=3x2-5xy+6y2,N=3y2-xy+x2,化简M-2N.
解析
∵M=3x2-5xy+6y2,N=3y2-xy+x2,
∴M-2N=(3x2-5xy+6y2)-2(3y2-xy+x2)
=3x2-5xy+6y2-6y2+2xy-2x2
=x2-3xy.
特别提示
将M和N看成一个整体代入,代入时,为防止出现符号错误,注意添加括号.
知识点二
整式的化简求值
整式化简求值的步骤:
一化:化简
二代:代入求值
三计算:进行计算
经典例题
题型一
多项式的值与某个字母无关的问题
例1
已知(2x2+ax-y+b)-(2bx2-3x+5y-1)的值与字母x的取值无关,求3(a2-ab-b2)-(4a2+ab+b2)的值.
解析
(2x2+ax-y+b)-(2bx2-3x+5y-1)
=2x2+ax-y+b-2bx2+3x-5y+1
=(2-2b)x2+(a+3)x+(-y-5y+b+1).
由题意可知2-2b=0,a+3=0,所以b=1,a=-3.
3(a2-ab-b2)-(4a2+ab+b2)
=3a2-3ab-3b2-4a2-ab-b2
=-a2-4ab-4b2.
当b=1,a=-3时,
原式=-(-3)2-4x(-3)x1-4x12=-1.
点拨
整式经过化简后,若含某个字母的项的系数都等于0,则这个整式的值与该字母的取值无关;反之当某个整式的值与某个字母的取值无关时,则整式中含该字母的项的系数都等于0.
题型二
整式加减的实际应用
例2
已知一个三角形的第一条边长为(a+3b)厘米,第二条边比第一条边短(b-1)厘米,第三条边比第二条边长3厘米.
(1)请用式子表示该三角形的周长;
(2)当a=2b=3时,求此三角形的周长.
解析
(1)根据题意,得第二条边长为(a+3b)-(b-1)=(a+2b+1)厘米,第三条边长为a+2b+1+3=(a+2b+4)厘米,所以该三角形的周长为(a+3b)+(a+2b+1)+(a+2b+4)=(3a+7b+5)厘米.
(2)当a=2,b=3时,此三角形的周长为3a+7b+5=6+21+5=32(厘米).
解析
(1)根据题意,得第二条边长为(a+3b)-(b-1)=(a+2b+1)厘米,第三条边长为a+2b+1+3=(a+2b+4)厘米,所以该三角形的周长为(a+3b)+(a+2b+1)+(a+2b+4)=(3a+7b+5)厘米.
(2)当a=2,b=3时,此三角形的周长为3a+7b+5=6+21+5=32(厘米).
特别提示
正确求出第二条边和第三条边的长是解此题的关键.
