甘肃省天水市田家炳高中2020-2021学年高二下学期期末考试数学(理)试题( Word版含答案)
文档属性
| 名称 | 甘肃省天水市田家炳高中2020-2021学年高二下学期期末考试数学(理)试题( Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 757.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-18 14:16:18 | ||
图片预览




文档简介
天水市田家炳中学2020-2021学年高二下学期期末考试
数学(理科)
一、选择题:本题共12题,每小题5分,共60分,在每小题给出的四个选项中,只有一项符合题目的要求.
1.若i是虚数单位,复数,则z的共扼复数在复平面上对应的点位于(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
2.已知全集,集合,,则(
)
A.
B.
C.
D.
3.在各项均为正数的等比数列中,,,则数列的前10项和等于(
)
A.511
B.512
C.1024
D.1023
4.某射手射击所得环数的分布列如下:
7
8
9
10
x
0.1
0.3
y
已知的期望,则y的值(
)
A.0.4
B.0.6
C.0.7
D.0.9
5.已知的展开式中的常数项为-160,则实数(
)
A.2
B.-2
C.8
D.-8
6.已知函数在处有极值10,则(
)
A.
B.0
C.或0
D.或6
7.2020年11月,兰州地铁2号线二期开通试运营.甲、乙、丙、丁四位同学决定乘坐地铁去兰州老街、西固公园、西站十字,每人只能去一个地方,西站十字一定要有人去,则不同游览方案的种数为(
)
A.60
B.75
C.70
D.65
8.一个几何体的三视图如图所示,则该几何体的表面积为(
)
A.38
B.26
C.40
D.33
9.若圆心坐标为的圆被直线截得的弦长为,则这个圆的方程是(
)
A.
B.
C.
D.
10.设函数,则下列函数中为奇函数的是(
)
A.
B.
C.
D.
11.已知双曲线的左、右焦点分别为,,P为C上一点,,O为坐标原点,若,则(
)
A.10
B.1或9
C.1
D.9
12.已知定义在R上的函数满足,且对任意都有,若,,,则下面结论正确的是(
)
A.
B.
C.
D.
二、填空题:本题共4小题,每题5分,共20分.
13.如果随机变量,且,且,则__________.
14.已知实数x,y满足,则的最大值为____________.
15.在正方体中,M,N分别为AD,的中点,O为侧面的中心,则异面直线MN与所成角的余弦值为______.
16.某射手射击?1?次,击中目标的概率是?0.9?,他连续射击?4?次,且各次射击是否击中目标相互之间没有影响,有下列结论:
①他第?3?次击中目标的概率是?0.9?;
②他恰好击中目标?3?次的概率是??;
③他至少击中目标?1?次的概率是??.
其中正确结论的序号是____________.?(写出所有正确结论的序号).
三、解答题:共70分,其中17题10分,18--22题每题12分.
17.已知.为数列的前项n和,已知,
(1)求的通项公式;
(2)设,求数列的前项n和.
18.如图,在三棱锥中,,,,平面平面,分别为,中点.
(1)求证:;
(2)求二面角的大小.
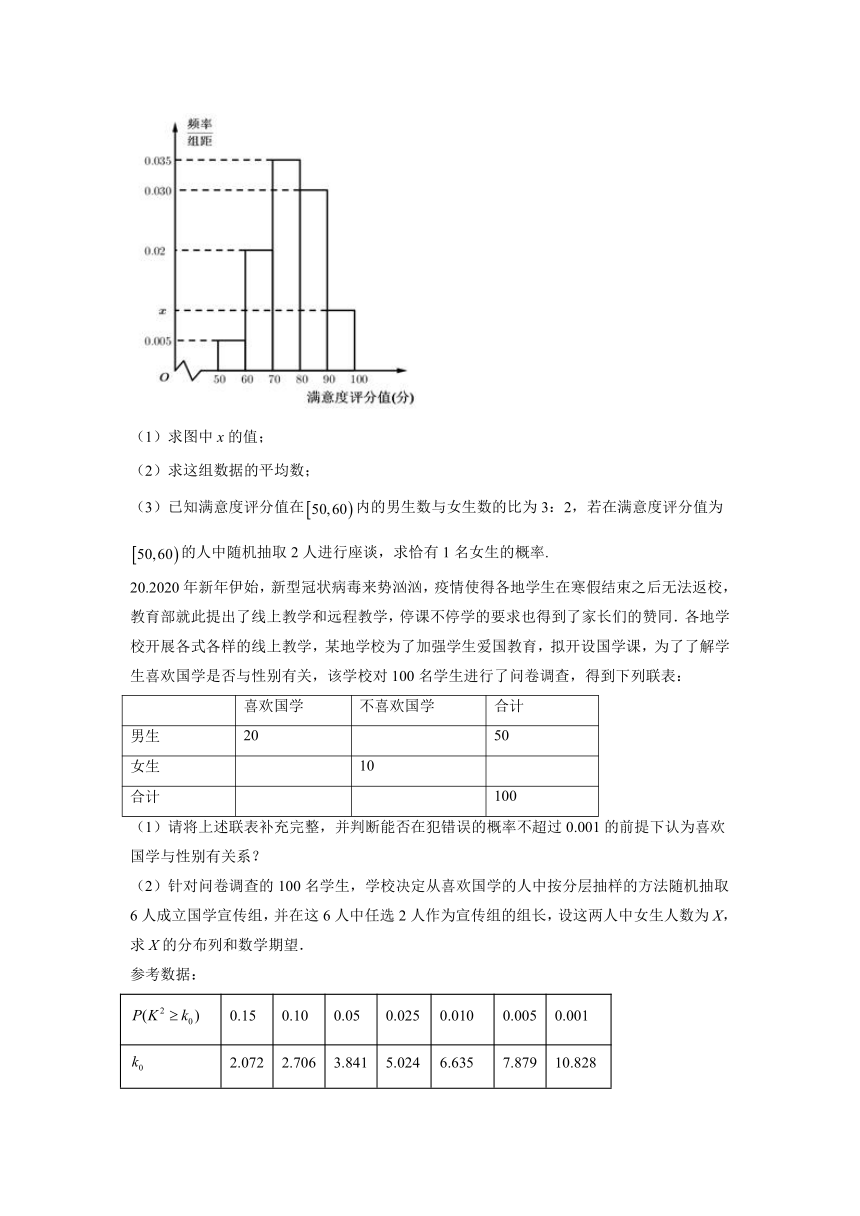
19.某部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照,,…分成5组,制成如图所示频率分布直方图.
(1)求图中x的值;
(2)求这组数据的平均数;
(3)已知满意度评分值在内的男生数与女生数的比为3:2,若在满意度评分值为的人中随机抽取2人进行座谈,求恰有1名女生的概率.
20.2020年新年伊始,新型冠状病毒来势汹汹,疫情使得各地学生在寒假结束之后无法返校,教育部就此提出了线上教学和远程教学,停课不停学的要求也得到了家长们的赞同.各地学校开展各式各样的线上教学,某地学校为了加强学生爱国教育,拟开设国学课,为了了解学生喜欢国学是否与性别有关,该学校对100名学生进行了问卷调查,得到下列联表:
喜欢国学
不喜欢国学
合计
男生
20
50
女生
10
合计
100
(1)请将上述联表补充完整,并判断能否在犯错误的概率不超过0.001的前提下认为喜欢国学与性别有关系?
(2)针对问卷调查的100名学生,学校决定从喜欢国学的人中按分层抽样的方法随机抽取6人成立国学宣传组,并在这6人中任选2人作为宣传组的组长,设这两人中女生人数为X,求X的分布列和数学期望.
参考数据:
0.15
0.10
0.05
0.025
0.010
0.005
0.001
2.072
2.706
3.841
5.024
6.635
7.879
10.828
,.
21.已知抛物线的焦点为上的一点到焦点的距离是5,
(1)求抛物线的方程
(2).过作直线,交于两点,若线段中点的纵坐标为-1,求直线的方程
22.已知函数(,e为自然对数的底数)
(1)若在点处的切线方程为,求a的值;
(2)讨论的单调性.
高二理数参考答案
1.A
2.B
3.D
4.A
5.B
6.A
7.D
8.A
9.B
10
D
11.D
12.C
12.解析:因为,得函数关于对称,
又对任意都有,所以函数在时单调递减,
因为,所以,
又,所以,所以,故选C.
13.答案:0.1587
解析:对正态分布,,
,
观察上图得,
.
故答案为:0.1587.
14.
15.
16.①③
17.(1)当时,
,
因为,所以.
当时,
,
即,
因为,所以.
所以数列是首项为,公差为的等差数列,
所以;
(2)由知,
所以数列前项和为:
18.答案:(1)
连接.因为,所以.因为,,
所以.又,所以平面.而平面,所以.
(2)
因为
平面平面且交于,,所以平面,则以
D为原点建立空间直角坐标系,如图:所以,,,
所以,.设平面的法向量,
所以令,得.平面,所以平面的法向量为.
由图知,由图知,所以,即二面角
的大小为.
19.答案:(1)由,解得;
(2)这组数据的平均数为;
(3)满意度评分值在内有人,男生数与女生数的比为3:2,故男生3人,女生2人,记为,记“满意度评分值为的人中随机抽取2人进行座谈,恰有1名女生”为事件A,
从5人中抽取2人有:,,,,,,,,,
,所以总基本事件个数为10个,A包含的基本事件:,,,,,,共6个,所以.
20.答案:(1)补充完整的列联表如下:
喜欢国学
不喜欢国学
合计
男生
20
30
50
女生
40
10
50
合计
60
40
100
计算得.
所以能在犯错误的概率不超过0.001的前提下认为喜欢国学与性别有关系.
(2)喜欢国学的共60人,按分层抽样抽取6人,则每人被抽到的概率均为,
从而需抽取男生2人,女生4人,
故的所有可能取值为0,1,2.
,
,
故的分布列为:
0
1
2
数学期望.
21.答案:1.由抛物线的定义得:
所以抛物线的方程为
2.由上可知
因为中点的纵坐标-1
设点
则,两式相减整理化简得
所求直线方程为:
22.解:(1)切线经过点.
,即,解得.
(2).
时,,可得在上单调递增,在上单调递减.
时,令,解得,
令,解得.
时,,则函数在上单调递增,在上单调递减,在上单调递增.
时,,函数在R上单调递增.
时,,则函数在上单调递增,在上单调递减,在上单调递增.
综上可得:当时,在上单调递增,在上单调递减.
当时,函数在上单调递增,在上单调递减,在上单调递增.
当时,函数在R上单调递增.
当时,函数在上单调递增,在上单调递减,在上单调递增.
数学(理科)
一、选择题:本题共12题,每小题5分,共60分,在每小题给出的四个选项中,只有一项符合题目的要求.
1.若i是虚数单位,复数,则z的共扼复数在复平面上对应的点位于(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
2.已知全集,集合,,则(
)
A.
B.
C.
D.
3.在各项均为正数的等比数列中,,,则数列的前10项和等于(
)
A.511
B.512
C.1024
D.1023
4.某射手射击所得环数的分布列如下:
7
8
9
10
x
0.1
0.3
y
已知的期望,则y的值(
)
A.0.4
B.0.6
C.0.7
D.0.9
5.已知的展开式中的常数项为-160,则实数(
)
A.2
B.-2
C.8
D.-8
6.已知函数在处有极值10,则(
)
A.
B.0
C.或0
D.或6
7.2020年11月,兰州地铁2号线二期开通试运营.甲、乙、丙、丁四位同学决定乘坐地铁去兰州老街、西固公园、西站十字,每人只能去一个地方,西站十字一定要有人去,则不同游览方案的种数为(
)
A.60
B.75
C.70
D.65
8.一个几何体的三视图如图所示,则该几何体的表面积为(
)
A.38
B.26
C.40
D.33
9.若圆心坐标为的圆被直线截得的弦长为,则这个圆的方程是(
)
A.
B.
C.
D.
10.设函数,则下列函数中为奇函数的是(
)
A.
B.
C.
D.
11.已知双曲线的左、右焦点分别为,,P为C上一点,,O为坐标原点,若,则(
)
A.10
B.1或9
C.1
D.9
12.已知定义在R上的函数满足,且对任意都有,若,,,则下面结论正确的是(
)
A.
B.
C.
D.
二、填空题:本题共4小题,每题5分,共20分.
13.如果随机变量,且,且,则__________.
14.已知实数x,y满足,则的最大值为____________.
15.在正方体中,M,N分别为AD,的中点,O为侧面的中心,则异面直线MN与所成角的余弦值为______.
16.某射手射击?1?次,击中目标的概率是?0.9?,他连续射击?4?次,且各次射击是否击中目标相互之间没有影响,有下列结论:
①他第?3?次击中目标的概率是?0.9?;
②他恰好击中目标?3?次的概率是??;
③他至少击中目标?1?次的概率是??.
其中正确结论的序号是____________.?(写出所有正确结论的序号).
三、解答题:共70分,其中17题10分,18--22题每题12分.
17.已知.为数列的前项n和,已知,
(1)求的通项公式;
(2)设,求数列的前项n和.
18.如图,在三棱锥中,,,,平面平面,分别为,中点.
(1)求证:;
(2)求二面角的大小.
19.某部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照,,…分成5组,制成如图所示频率分布直方图.
(1)求图中x的值;
(2)求这组数据的平均数;
(3)已知满意度评分值在内的男生数与女生数的比为3:2,若在满意度评分值为的人中随机抽取2人进行座谈,求恰有1名女生的概率.
20.2020年新年伊始,新型冠状病毒来势汹汹,疫情使得各地学生在寒假结束之后无法返校,教育部就此提出了线上教学和远程教学,停课不停学的要求也得到了家长们的赞同.各地学校开展各式各样的线上教学,某地学校为了加强学生爱国教育,拟开设国学课,为了了解学生喜欢国学是否与性别有关,该学校对100名学生进行了问卷调查,得到下列联表:
喜欢国学
不喜欢国学
合计
男生
20
50
女生
10
合计
100
(1)请将上述联表补充完整,并判断能否在犯错误的概率不超过0.001的前提下认为喜欢国学与性别有关系?
(2)针对问卷调查的100名学生,学校决定从喜欢国学的人中按分层抽样的方法随机抽取6人成立国学宣传组,并在这6人中任选2人作为宣传组的组长,设这两人中女生人数为X,求X的分布列和数学期望.
参考数据:
0.15
0.10
0.05
0.025
0.010
0.005
0.001
2.072
2.706
3.841
5.024
6.635
7.879
10.828
,.
21.已知抛物线的焦点为上的一点到焦点的距离是5,
(1)求抛物线的方程
(2).过作直线,交于两点,若线段中点的纵坐标为-1,求直线的方程
22.已知函数(,e为自然对数的底数)
(1)若在点处的切线方程为,求a的值;
(2)讨论的单调性.
高二理数参考答案
1.A
2.B
3.D
4.A
5.B
6.A
7.D
8.A
9.B
10
D
11.D
12.C
12.解析:因为,得函数关于对称,
又对任意都有,所以函数在时单调递减,
因为,所以,
又,所以,所以,故选C.
13.答案:0.1587
解析:对正态分布,,
,
观察上图得,
.
故答案为:0.1587.
14.
15.
16.①③
17.(1)当时,
,
因为,所以.
当时,
,
即,
因为,所以.
所以数列是首项为,公差为的等差数列,
所以;
(2)由知,
所以数列前项和为:
18.答案:(1)
连接.因为,所以.因为,,
所以.又,所以平面.而平面,所以.
(2)
因为
平面平面且交于,,所以平面,则以
D为原点建立空间直角坐标系,如图:所以,,,
所以,.设平面的法向量,
所以令,得.平面,所以平面的法向量为.
由图知,由图知,所以,即二面角
的大小为.
19.答案:(1)由,解得;
(2)这组数据的平均数为;
(3)满意度评分值在内有人,男生数与女生数的比为3:2,故男生3人,女生2人,记为,记“满意度评分值为的人中随机抽取2人进行座谈,恰有1名女生”为事件A,
从5人中抽取2人有:,,,,,,,,,
,所以总基本事件个数为10个,A包含的基本事件:,,,,,,共6个,所以.
20.答案:(1)补充完整的列联表如下:
喜欢国学
不喜欢国学
合计
男生
20
30
50
女生
40
10
50
合计
60
40
100
计算得.
所以能在犯错误的概率不超过0.001的前提下认为喜欢国学与性别有关系.
(2)喜欢国学的共60人,按分层抽样抽取6人,则每人被抽到的概率均为,
从而需抽取男生2人,女生4人,
故的所有可能取值为0,1,2.
,
,
故的分布列为:
0
1
2
数学期望.
21.答案:1.由抛物线的定义得:
所以抛物线的方程为
2.由上可知
因为中点的纵坐标-1
设点
则,两式相减整理化简得
所求直线方程为:
22.解:(1)切线经过点.
,即,解得.
(2).
时,,可得在上单调递增,在上单调递减.
时,令,解得,
令,解得.
时,,则函数在上单调递增,在上单调递减,在上单调递增.
时,,函数在R上单调递增.
时,,则函数在上单调递增,在上单调递减,在上单调递增.
综上可得:当时,在上单调递增,在上单调递减.
当时,函数在上单调递增,在上单调递减,在上单调递增.
当时,函数在R上单调递增.
当时,函数在上单调递增,在上单调递减,在上单调递增.
同课章节目录
