332指数函数的图像和性质(第二课时) 课件(共31张PPT)——2021-2022学年高一上学期数学北师大版(2019)必修第一册
文档属性
| 名称 | 332指数函数的图像和性质(第二课时) 课件(共31张PPT)——2021-2022学年高一上学期数学北师大版(2019)必修第一册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-19 10:13:28 | ||
图片预览











文档简介
(共31张PPT)
3.3.2指数函数的图像和性质
第二课时
教学目标
本课时专讲含指数函数的奇偶性
含指数函数的奇偶性判证
重点
难点
含指数函数奇偶性的简单应用.
环节一
判断和证明
方法回顾
1.判断时,主要用图像和性质
2.证明时,主要用定义
例1.已知f(x)=,则下列正确的是( )
A.奇函数,在R上为增函数
B.偶函数,在R上为增函数
C.奇函数,在R上为减函数
D.偶函数,在R上为减函数
分析:图像是没法画的,所以无法通过图像的对称性判断奇偶性;拆开看,,非奇非偶,所以无法用性质判断奇偶性;只能用定义了。
例1.已知f(x)=,则下列正确的是( )
A.奇函数,在R上为增函数
B.偶函数,在R上为增函数
C.奇函数,在R上为减函数
D.偶函数,在R上为减函数
解:定义域是R,且,所以,函数是奇函数。由y=ex是增函数,y=e-x是减函数知,f(x)是增函数.选A.
例2.判断并证明函数的奇偶性
解析:只能用定义判断与证明.
定义域是R,关于原点对称
=
所以函数是奇函数
1.若函数f(x)=3x+3-x与g(x)=3x-3-x的定义域为R,则( )
A.f(x)与g(x)均为偶函数
B.f(x)为偶函数,g(x)为奇函数
C.f(x)与g(x)均为奇函数
D.f(x)为奇函数,g(x)为偶函数
微练
解析:f(-x)=3-x+3x=f(x),f(x)为偶函数,g(-x)=3-x-3x=-g(x),g(x)为奇函数.
2.已知函数f(x)=(a>0,且a≠1).
讨论f(x)的奇偶性;
因为f(x)的定义域为R,
且f(-x)==-f(x),
所以f(x)是奇函数.
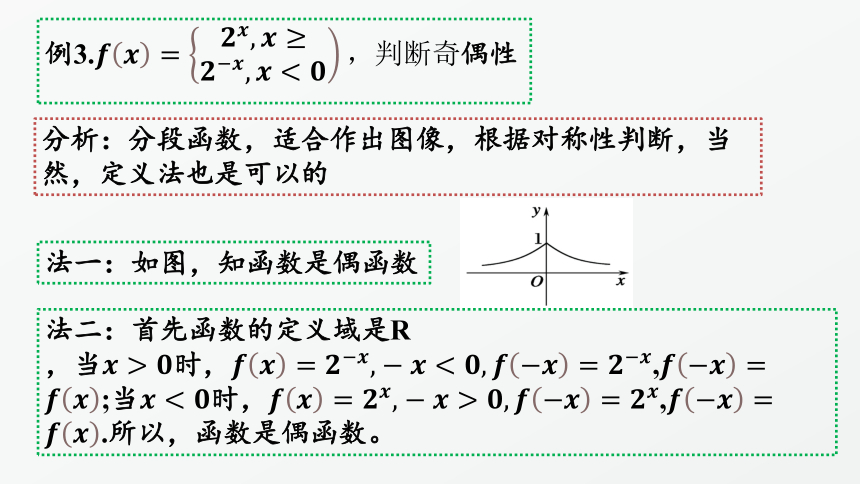
例3.偶性
分析:分段函数,适合作出图像,根据对称性判断,当然,定义法也是可以的
法一:如图,知函数是偶函数
法二:首先函数的定义域是R
,当时,,;当时,,.所以,函数是偶函数。
微练
已知分段函数
提示:按时分别用定义判证。结果是奇函数。
环节二
奇偶性求值
例4.设为定义在上R奇函数,当时,,则
分析1:可以先求再求
解:
分析2:可以先求再求
解:,,所以,。
环节三
奇偶性求解析式
例5.已知定义为R的函数是奇函数,当时,,求解析式
解析:①函数是奇函数,所以
②,所以,=
综上可知,
易错点:
1.忽略x=0;
2.结果不写成分段函数形式。
为定义上奇函数,当时,解析式为,求在上的解析式
析:不用单独考查设,.
微练
例6.已知R上偶函数f(x)和奇函数g(x),,求它们的解析式。
分析:条件中的函数关系式是由两个函数共同构成,需要借助性质再添加一个关系式,联立解出解析式。在以前的题型中,这种求解析式的方法叫解方程组法
解:
f(?)??(?)=4?
由性质知,两式相加减得,
环节四
奇偶性求参
例7.已知定义域为R的函数f(x)=是奇函数.求a,b的值;
解:f(x)为奇函数且在x=0处有意义,
∴f(0)=0,即=0,∴b=1,
∴f(x)=.又∵f(-1)=-f(1),
∴,∴a=2.
特色是,两次对奇函数用了特殊值。一般最常用的是f(0)=0
微练
1.已知函数是否存在实数a,使函数为奇函数?
提示:定义域是R,在x=0处有意义,f(0)=0,得a=1.
2.已知函数,定义在R上奇函数,求a
提示:由f(0)=0得,a=3
例8.已知定义在R上奇函数),求a
解:由+,所以
本方法的亮点是用定义求参,前面几道题侧重于用特值求参。
例9.已知分段函数,是偶函数,则a的值
解:从特殊值法,偶函数没有f(0)=0,可以换成f(-1)=f(1),即
从定义法,两者相等,得
环节五
伪奇函数求值
例10.+1,在上最大值M,最小值m,则求M+m
解:先函数分拆开看,,证明过是偶函数,是奇函数,=
+1.
M=,M+m=0+2=2
所谓伪奇函数,是指一个函数是一个奇函数与一个常函数和或差的形式。核心知识是奇函数。
环节六
奇偶性与单调性结合
这种问题在本节课不是研究方向,专题研究的内容,放在下一个课时。敬请关注。
例11.已知函数f(x)=a-(x∈R).
(1)用定义证明:不论a为何实数,f(x)在(-∞,+∞)上为增函数;
(2)若f(x)为奇函数,求a的值;
(3)在(2)的条件下,求f(x)在区间[1,5]上的最小值.
解:(1)证明:f(x)的定义域为R,
设x1,x2是R上的任意两个不相等的实数,且x1因为
所以不管a为何值,在R上为增函数
函数
由(2)知,f(x)在(-∞,+∞)上为增函数,∴f(x)在区间[1,5]上的最小值为f(1).∵f(1)=-=,∴f(x)在区间[1,5]上的最小值为.
课堂小结
1.核心要点
含指数函数的奇偶性判证与求式求值求参等方面的应用
2.数学素养
体会数学抽象的过程,强化直观想象素养的培养.
谢谢观看
课件制作老师:胡琪
3.3.2指数函数的图像和性质
第二课时
教学目标
本课时专讲含指数函数的奇偶性
含指数函数的奇偶性判证
重点
难点
含指数函数奇偶性的简单应用.
环节一
判断和证明
方法回顾
1.判断时,主要用图像和性质
2.证明时,主要用定义
例1.已知f(x)=,则下列正确的是( )
A.奇函数,在R上为增函数
B.偶函数,在R上为增函数
C.奇函数,在R上为减函数
D.偶函数,在R上为减函数
分析:图像是没法画的,所以无法通过图像的对称性判断奇偶性;拆开看,,非奇非偶,所以无法用性质判断奇偶性;只能用定义了。
例1.已知f(x)=,则下列正确的是( )
A.奇函数,在R上为增函数
B.偶函数,在R上为增函数
C.奇函数,在R上为减函数
D.偶函数,在R上为减函数
解:定义域是R,且,所以,函数是奇函数。由y=ex是增函数,y=e-x是减函数知,f(x)是增函数.选A.
例2.判断并证明函数的奇偶性
解析:只能用定义判断与证明.
定义域是R,关于原点对称
=
所以函数是奇函数
1.若函数f(x)=3x+3-x与g(x)=3x-3-x的定义域为R,则( )
A.f(x)与g(x)均为偶函数
B.f(x)为偶函数,g(x)为奇函数
C.f(x)与g(x)均为奇函数
D.f(x)为奇函数,g(x)为偶函数
微练
解析:f(-x)=3-x+3x=f(x),f(x)为偶函数,g(-x)=3-x-3x=-g(x),g(x)为奇函数.
2.已知函数f(x)=(a>0,且a≠1).
讨论f(x)的奇偶性;
因为f(x)的定义域为R,
且f(-x)==-f(x),
所以f(x)是奇函数.
例3.偶性
分析:分段函数,适合作出图像,根据对称性判断,当然,定义法也是可以的
法一:如图,知函数是偶函数
法二:首先函数的定义域是R
,当时,,;当时,,.所以,函数是偶函数。
微练
已知分段函数
提示:按时分别用定义判证。结果是奇函数。
环节二
奇偶性求值
例4.设为定义在上R奇函数,当时,,则
分析1:可以先求再求
解:
分析2:可以先求再求
解:,,所以,。
环节三
奇偶性求解析式
例5.已知定义为R的函数是奇函数,当时,,求解析式
解析:①函数是奇函数,所以
②,所以,=
综上可知,
易错点:
1.忽略x=0;
2.结果不写成分段函数形式。
为定义上奇函数,当时,解析式为,求在上的解析式
析:不用单独考查设,.
微练
例6.已知R上偶函数f(x)和奇函数g(x),,求它们的解析式。
分析:条件中的函数关系式是由两个函数共同构成,需要借助性质再添加一个关系式,联立解出解析式。在以前的题型中,这种求解析式的方法叫解方程组法
解:
f(?)??(?)=4?
由性质知,两式相加减得,
环节四
奇偶性求参
例7.已知定义域为R的函数f(x)=是奇函数.求a,b的值;
解:f(x)为奇函数且在x=0处有意义,
∴f(0)=0,即=0,∴b=1,
∴f(x)=.又∵f(-1)=-f(1),
∴,∴a=2.
特色是,两次对奇函数用了特殊值。一般最常用的是f(0)=0
微练
1.已知函数是否存在实数a,使函数为奇函数?
提示:定义域是R,在x=0处有意义,f(0)=0,得a=1.
2.已知函数,定义在R上奇函数,求a
提示:由f(0)=0得,a=3
例8.已知定义在R上奇函数),求a
解:由+,所以
本方法的亮点是用定义求参,前面几道题侧重于用特值求参。
例9.已知分段函数,是偶函数,则a的值
解:从特殊值法,偶函数没有f(0)=0,可以换成f(-1)=f(1),即
从定义法,两者相等,得
环节五
伪奇函数求值
例10.+1,在上最大值M,最小值m,则求M+m
解:先函数分拆开看,,证明过是偶函数,是奇函数,=
+1.
M=,M+m=0+2=2
所谓伪奇函数,是指一个函数是一个奇函数与一个常函数和或差的形式。核心知识是奇函数。
环节六
奇偶性与单调性结合
这种问题在本节课不是研究方向,专题研究的内容,放在下一个课时。敬请关注。
例11.已知函数f(x)=a-(x∈R).
(1)用定义证明:不论a为何实数,f(x)在(-∞,+∞)上为增函数;
(2)若f(x)为奇函数,求a的值;
(3)在(2)的条件下,求f(x)在区间[1,5]上的最小值.
解:(1)证明:f(x)的定义域为R,
设x1,x2是R上的任意两个不相等的实数,且x1
所以不管a为何值,在R上为增函数
函数
由(2)知,f(x)在(-∞,+∞)上为增函数,∴f(x)在区间[1,5]上的最小值为f(1).∵f(1)=-=,∴f(x)在区间[1,5]上的最小值为.
课堂小结
1.核心要点
含指数函数的奇偶性判证与求式求值求参等方面的应用
2.数学素养
体会数学抽象的过程,强化直观想象素养的培养.
谢谢观看
课件制作老师:胡琪
