2021-2022学年青岛版数学八年级上册期中测试题(word版含答案)
文档属性
| 名称 | 2021-2022学年青岛版数学八年级上册期中测试题(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 125.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-20 16:31:15 | ||
图片预览


文档简介
青岛版数学八年级上册期中测试题
(时间:120分钟
分值:100分)
一、选择题(共10小题,每小题4分,满分40分)
1.(4分)图中全等的三角形是( )
A.Ⅰ和Ⅱ
B.Ⅱ和Ⅳ
C.Ⅱ和Ⅲ
D.Ⅰ和Ⅲ
2.(4分)如图,用∠B=∠D,∠1=∠2直接判定△ABC≌△ADC的理由是( )
A.AAS
B.SSS
C.ASA
D.SAS
3.(4分)如图,AC与BD相交于点E,BE=ED,AE=EC,则△ABE≌△CDE的理由是( )
A.ASA
B.SAS
C.AAS
D.SSS
4.(4分)如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( )
A.带①去
B.带②去
C.带③去
D.带①和②去
5.(4分)已知:如图,CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD相交于O点,∠1=∠2.图中全等的三角形共有( )
A.4对
B.3对
C.2对
D.1对
6.(4分)如图,下列图案是我国几家银行的标志,其中不是轴对称图形的是( )
A.
B.
C.
D.
7.(4分)如下书写的四个汉字,其中为轴对称图形的是( )
A.
B.
C.
D.
8.(4分)如图,有A、B、C三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )
A.在AC,BC两边高线的交点处
B.在AC,BC两边中线的交点处
C.在AC,BC两边垂直平分线的交点处
D.在∠A,∠B两内角平分线的交点处
9.(4分)如图,直线l1、l2、l3分别表示三条相互交叉的公路,现要建立一个货物中转站,要求它到三条公路的距离相等,则可选择的地址有( )
A.一处
B.二处
C.三处
D.四处
10.(4分)等腰三角形的对称轴是( )
A.顶角的平分线
B.底边上的高
C.底边上的中线
D.底边上的高所在的直线
二、填空题(共6小题,每小题3分,满分18分)
11.(3分)如图,在△ABC和△DEF中,如果AB=DE,AC=DF,只要再具备条件
,就可以证明△ABC≌△DEF.
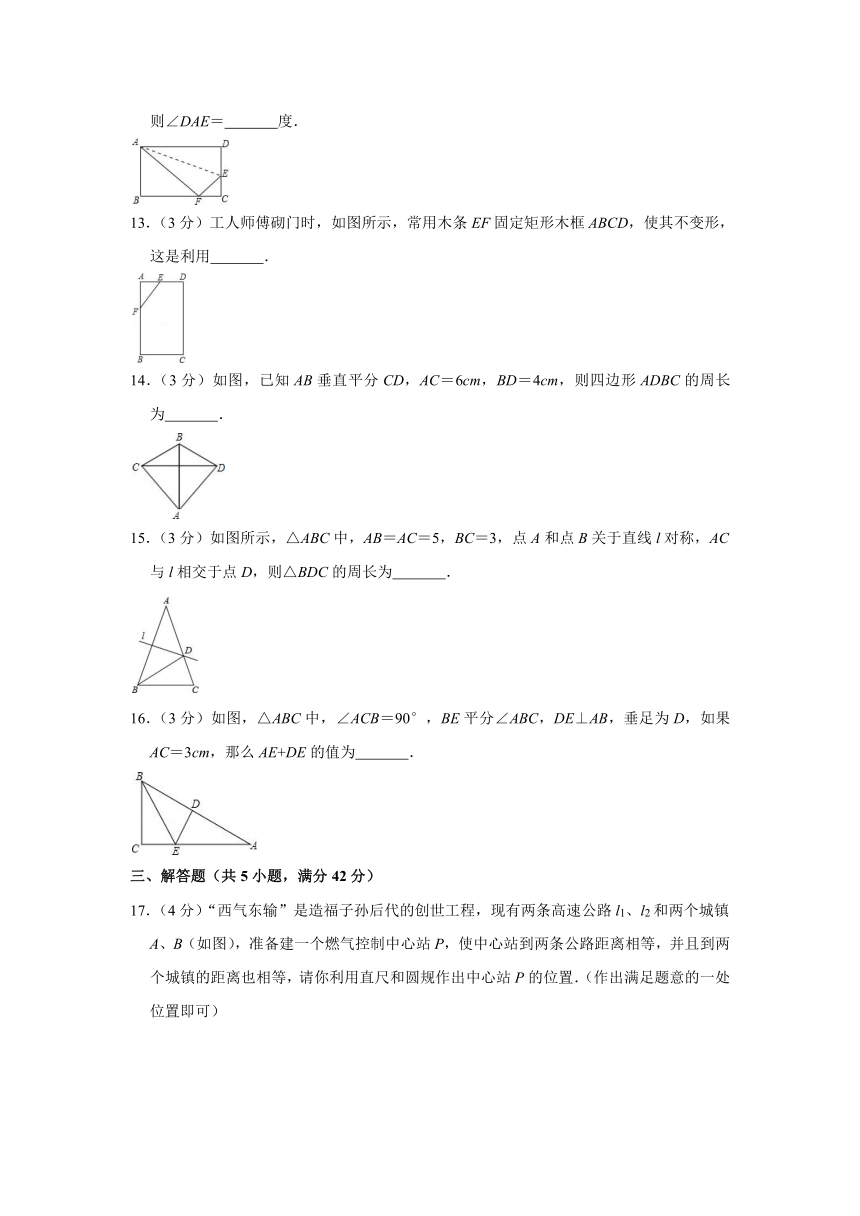
12.(3分)如图,矩形ABCD沿AE折叠,使D点落在BC边上点F处,如果∠BAF=60°,则∠DAE=
度.
13.(3分)工人师傅砌门时,如图所示,常用木条EF固定矩形木框ABCD,使其不变形,这是利用
.
14.(3分)如图,已知AB垂直平分CD,AC=6cm,BD=4cm,则四边形ADBC的周长为
.
15.(3分)如图所示,△ABC中,AB=AC=5,BC=3,点A和点B关于直线l对称,AC与l相交于点D,则△BDC的周长为
.
16.(3分)如图,△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB,垂足为D,如果AC=3cm,那么AE+DE的值为
.
三、解答题(共5小题,满分42分)
17.(4分)“西气东输”是造福子孙后代的创世工程,现有两条高速公路l1、l2和两个城镇A、B(如图),准备建一个燃气控制中心站P,使中心站到两条公路距离相等,并且到两个城镇的距离也相等,请你利用直尺和圆规作出中心站P的位置.(作出满足题意的一处位置即可)
18.(9分)如图,CD=CA,∠1=∠2,EC=BC,与DE相等的线段是哪一条?说明理由.
19.(9分)如图,点B、C、E、F在同一直线上,AB∥DE,∠A=∠D,BF=CE
求证:AB=DE.
20.(10分)已知:点D是△ABC的边BC的中点,DE⊥AC,DF⊥AB,垂足分别为E,F,且BF=CE.求证:△ABC是等腰三角形.
21.(10分)等边△ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ,问△APQ是什么形状的三角形?试说明你的结论.
参考答案
一、选择题。
1.D.
2.A.
3.B.
4.C.
5.A.
6.C.
7.B.
8.C.
9.D.
10.D.
二、填空题。
11.BC=EF或∠A=∠D.
12.15.
13.三角形的稳定性.
14.20cm.
15.8.
16.3cm.
三、解答题。
17.
解:
作出角平分线、线段AB的垂直平分线各(2分),标出点P得(1分)
18.解:DE=AB.理由如下:
∵∠1=∠2,
∴∠1+ACE=∠2+∠ACE,
即∠ACB=∠DCE,
在△ABC和△DCE中,
,
∴△ACB≌△DCE(SAS),
∴AB=DE.
19.证明:∵AB∥DE,BF=CE,
∴∠B=∠E,BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(AAS),
∴AB=DE.
20.证明:∵D是BC的中点,
∴BD=CD,
∵DE⊥AC,DF⊥AB,
∴△BDF与△CDE为直角三角形,
在Rt△BDF和Rt△CDE中,
,
∴Rt△BFD≌Rt△CED(HL),
∴∠B=∠C,
∴AB=AC,
∴△ABC是等腰三角形.
21.解:△APQ为等边三角形.
证明:∵△ABC为等边三角形,
∴AB=AC.
在△ABP与△ACQ中,
∵,
∴△ABP≌△ACQ(SAS).
∴AP=AQ,∠BAP=∠CAQ.
∵∠BAC=∠BAP+∠PAC=60°,
∴∠PAQ=∠CAQ+∠PAC=60°,
∴△APQ是等边三角形.
(时间:120分钟
分值:100分)
一、选择题(共10小题,每小题4分,满分40分)
1.(4分)图中全等的三角形是( )
A.Ⅰ和Ⅱ
B.Ⅱ和Ⅳ
C.Ⅱ和Ⅲ
D.Ⅰ和Ⅲ
2.(4分)如图,用∠B=∠D,∠1=∠2直接判定△ABC≌△ADC的理由是( )
A.AAS
B.SSS
C.ASA
D.SAS
3.(4分)如图,AC与BD相交于点E,BE=ED,AE=EC,则△ABE≌△CDE的理由是( )
A.ASA
B.SAS
C.AAS
D.SSS
4.(4分)如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( )
A.带①去
B.带②去
C.带③去
D.带①和②去
5.(4分)已知:如图,CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD相交于O点,∠1=∠2.图中全等的三角形共有( )
A.4对
B.3对
C.2对
D.1对
6.(4分)如图,下列图案是我国几家银行的标志,其中不是轴对称图形的是( )
A.
B.
C.
D.
7.(4分)如下书写的四个汉字,其中为轴对称图形的是( )
A.
B.
C.
D.
8.(4分)如图,有A、B、C三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )
A.在AC,BC两边高线的交点处
B.在AC,BC两边中线的交点处
C.在AC,BC两边垂直平分线的交点处
D.在∠A,∠B两内角平分线的交点处
9.(4分)如图,直线l1、l2、l3分别表示三条相互交叉的公路,现要建立一个货物中转站,要求它到三条公路的距离相等,则可选择的地址有( )
A.一处
B.二处
C.三处
D.四处
10.(4分)等腰三角形的对称轴是( )
A.顶角的平分线
B.底边上的高
C.底边上的中线
D.底边上的高所在的直线
二、填空题(共6小题,每小题3分,满分18分)
11.(3分)如图,在△ABC和△DEF中,如果AB=DE,AC=DF,只要再具备条件
,就可以证明△ABC≌△DEF.
12.(3分)如图,矩形ABCD沿AE折叠,使D点落在BC边上点F处,如果∠BAF=60°,则∠DAE=
度.
13.(3分)工人师傅砌门时,如图所示,常用木条EF固定矩形木框ABCD,使其不变形,这是利用
.
14.(3分)如图,已知AB垂直平分CD,AC=6cm,BD=4cm,则四边形ADBC的周长为
.
15.(3分)如图所示,△ABC中,AB=AC=5,BC=3,点A和点B关于直线l对称,AC与l相交于点D,则△BDC的周长为
.
16.(3分)如图,△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB,垂足为D,如果AC=3cm,那么AE+DE的值为
.
三、解答题(共5小题,满分42分)
17.(4分)“西气东输”是造福子孙后代的创世工程,现有两条高速公路l1、l2和两个城镇A、B(如图),准备建一个燃气控制中心站P,使中心站到两条公路距离相等,并且到两个城镇的距离也相等,请你利用直尺和圆规作出中心站P的位置.(作出满足题意的一处位置即可)
18.(9分)如图,CD=CA,∠1=∠2,EC=BC,与DE相等的线段是哪一条?说明理由.
19.(9分)如图,点B、C、E、F在同一直线上,AB∥DE,∠A=∠D,BF=CE
求证:AB=DE.
20.(10分)已知:点D是△ABC的边BC的中点,DE⊥AC,DF⊥AB,垂足分别为E,F,且BF=CE.求证:△ABC是等腰三角形.
21.(10分)等边△ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ,问△APQ是什么形状的三角形?试说明你的结论.
参考答案
一、选择题。
1.D.
2.A.
3.B.
4.C.
5.A.
6.C.
7.B.
8.C.
9.D.
10.D.
二、填空题。
11.BC=EF或∠A=∠D.
12.15.
13.三角形的稳定性.
14.20cm.
15.8.
16.3cm.
三、解答题。
17.
解:
作出角平分线、线段AB的垂直平分线各(2分),标出点P得(1分)
18.解:DE=AB.理由如下:
∵∠1=∠2,
∴∠1+ACE=∠2+∠ACE,
即∠ACB=∠DCE,
在△ABC和△DCE中,
,
∴△ACB≌△DCE(SAS),
∴AB=DE.
19.证明:∵AB∥DE,BF=CE,
∴∠B=∠E,BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(AAS),
∴AB=DE.
20.证明:∵D是BC的中点,
∴BD=CD,
∵DE⊥AC,DF⊥AB,
∴△BDF与△CDE为直角三角形,
在Rt△BDF和Rt△CDE中,
,
∴Rt△BFD≌Rt△CED(HL),
∴∠B=∠C,
∴AB=AC,
∴△ABC是等腰三角形.
21.解:△APQ为等边三角形.
证明:∵△ABC为等边三角形,
∴AB=AC.
在△ABP与△ACQ中,
∵,
∴△ABP≌△ACQ(SAS).
∴AP=AQ,∠BAP=∠CAQ.
∵∠BAC=∠BAP+∠PAC=60°,
∴∠PAQ=∠CAQ+∠PAC=60°,
∴△APQ是等边三角形.
同课章节目录
